DIRECT GRADIENT-BASED REINFORCEMENT LEARNING

FOR ROBOT BEHAVIOR LEARNING

Andres El-Fakdi, Marc Carreras and Pere Ridao

Institute of Informatics and Applications, University of Girona, Politecnica 4, Campus Montilivi, 17071 Girona, Spain

Keywords: Robot Learning, Autonomous robots.

Abstract: Autonomous Underwater Vehicles (AUV) represent a challenging control problem with complex, noisy,

dynamics. Nowadays, not only the continuous scientific advances in underwater robotics but the increasing

number of sub sea missions and its complexity ask for an automatization of submarine processes. This paper

proposes a high-level control system for solving the action selection problem of an autonomous robot. The

system is characterized by the use of Reinforcement Learning Direct Policy Search methods (RLDPS) for

learning the internal state/action mapping of some behaviors. We demonstrate its feasibility with simulated

experiments using the model of our underwater robot URIS in a target following task.

1 INTRODUCTION

A commonly used methodology in robot learning is

Reinforcement Learning (RL) (Sutton, 1998). In RL,

an agent tries to maximize a scalar evaluation

(reward or punishment) obtained as a result of its

interaction with the environment. The goal of a RL

system is to find an optimal policy which maps the

state of the environment to an action which in turn

will maximize the accumulated future rewards. Most

RL techniques are based on Finite Markov Decision

Processes (FMDP) causing finite state and action

spaces. The main advantage of RL is that it does not

use any knowledge database, so the learner is not

told what to do as occurs in most forms of machine

learning, but instead must discover actions yield the

most reward by trying them. Therefore, this class of

learning is suitable for online robot learning. The

main disadvantages are a long convergence time and

the lack of generalization among continuous

variables.

In order to solve such problems, most of RL

applications require the use of generalizing function

approximators such artificial neural-networks

(ANNs), instance-based methods or decision-trees.

As a result, many RL-based control systems have

been applied to robotics over the past decade. In

(Smart and Kaelbling, 2000), an instance-based

learning algorithm was applied to a real robot in a

corridor-following task. For the same task, in

(Hernandez and Mahadevan, 2000) a hierarchical

memory-based RL was proposed.

The dominant approach has been the value-

function approach, and although it has demonstrated

to work well in many applications, it has several

limitations, too. If the state-space is not completely

observable (POMDP), small changes in the

estimated value of an action cause it to be, or not be,

selected; and this will detonate in convergence

problems (Bertsekas and Tsitsiklis, 1996).

Over the past few years, studies have shown that

approximating directly a policy can be easier than

working with value functions, and better results can

be obtained (Sutton et al., 2000) (Anderson, 2000).

Instead of approximating a value function, new

methodologies approximate a policy using an

independent function approximator with its own

parameters, trying to maximize the expected reward.

Examples of direct policy methods are the

REINFORCE algorithm (Williams, 1992), the

direct-gradient algorithm (Baxter and Bartlett, 2000)

and certain variants of the actor-critic framework

(Konda and Tsitsiklis, 2003). Some direct policy

search methodologies have achieved good practical

results. Applications to autonomous helicopter flight

(Bagnell and Schneider, 2001), optimization of robot

locomotion movements (Kohl and Stone, 2004) and

robot weightlifting task (Rosenstein and Barto,

2001) are some examples.

The advantages of policy methods against value-

function based methods are various. A problem for

which the policy is easier to represent should be

solved using policy algorithms (Anderson, 2000).

Working this way should represent a decrease in the

225

El-Fakdi A., Carreras M. and Ridao P. (2005).

DIRECT GRADIENT-BASED REINFORCEMENT LEARNING FOR ROBOT BEHAVIOR LEARNING.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 225-231

DOI: 10.5220/0001188902250231

 SciTePress

computational complexity and, for learning control

systems which operate in the physical world, the

reduction in time-consuming would be notorious.

Furthermore, learning systems should be designed to

explicitly account for the resulting violations of the

Markov property. Studies have shown that stochastic

policy-only methods can obtain better results when

working in POMDP than those ones obtained with

deterministic value-function methods (Singh et al.,

1994). On the other side, policy methods learn much

more slowly than RL algorithms using value

function (Sutton et al., 2000) and they typically find

only local optima of the expected reward (Meuleau

et al., 2001).

In this paper we propose an on-line direct policy

search algorithm based on Baxter and Bartlett’s

direct-gradient algorithm OLPOMDP (Baxter and

Bartlett, 1999) applied to a real learning control

system in which a simulated model of the AUV

URIS (Ridao et al., 2004) navigates a two-

dimensional world. The policy is represented by a

neural network whose input is a representation of the

state, whose output is action selection probabilities,

and whose weights are the policy parameters. The

proposed method is based on a stochastic gradient

descent with respect to the policy parameter space, it

does not need a model of the environment to be

given and it is incremental, requiring only a constant

amount of computation step. The objective of the

agent is to compute a stochastic policy (Singh et al.,

1994), which assigns a probability over each action.

Results obtained in simulation show the viability of

the algorithm in a real-time system.

The structure of the paper is as follows. In

section II the direct-policy search algorithm is

detailed. In section III a description of all the

elements that affect our problem (the world, the

robot and the controller) are commented. The

simulated experiment description and the results

obtained are included in section IV and finally, some

conclusions and further work are included in section

2 THE RLDPS ALGORITHM

A partially observable Markov decision process

(POMDP) consists of a state space S, an observation

space Y and a control space U. For each state

iS∈

there is a deterministic reward r(i). As

mentioned before, the algorithm applied is designed to

work on-line so at every time step, the learner (our

vehicle) will be given an observation of the state and,

according to the policy followed at that moment, it will

generate a control action. As a result, the learner will be

driven to another state and will receive a reward

associated to this new state. This reward will allow us to

update the controller’s parameters that define the policy

followed at every iteration, resulting in a final policy

considered to be optimal or closer to optimal. The

algorithm procedure is summarized in Table 1.

Table 1: Algorithm: Baxter & Bartlett’s OLPOMDP

1: Given:

•

0T >

• Initial parameter values

∈

• Arbitrary starting state i

2: Set z

= 0 ( z

∈



)

3: for t = 0 to T do

4: Observe state y

5: Generate control action u

according to current policy

(, )

µθ

6: Observe the reward obtained r(i

t+1

)

7: Set

8: Set

9: end for

The algorithm works as follows: having

initialized the parameters vector

, the initial state

and the gradient

, the learning procedure

will be iterated T times. At every iteration, the

parameters gradient

z will be updated. According

to the immediate reward received

()

, the new

gradient vector

and a fixed learning

paramenter

, the new paramenter vector

can be

calculated. The current policy

is directly modified

by the new parameters becoming a new policy

that will be followed next iteration, getting

closer, as

tT→

to a final policy

that represents a

correct solution of the problem.

In order to clarify the steps taken, the next lines

will relate the update parameter procedure of the

algorithm closely. The controller uses a neural

network as a function approximator that generates a

stochastic policy. Its weights are the policy

parameters that are updated on-line every time step.

The accuracy of the approximation is controlled by

the parameter

[0,1)

∈

The first step in the weight update procedure is

to compute the ratio:

(, )

µθ

∇

111

()

tt tt

ri z

θα

ICINCO 2005 - ROBOTICS AND AUTOMATION

226

(, )

µθ

∇

(1)

for every weight of the network. In AANs like the

one used in the algorithm the expression defined in

step 7 of Table 1 can be rewritten as:

1tttt

zzy

(2)

At any step time t, the term

z represents the

estimated gradient of the reinforcement sum with

respect to the network’s layer weights. In addition,

refers to the local gradient associated to a single

neuron of the ANN and it is multiplied by the input

to that neuron

y . In order to compute these

gradients, we evaluate the soft-max distribution for

each possible future state exponentiating the real-

valued ANN outputs

{

}

,...,

oobeing n the number

of neurons of the output layer (Aberdeen

, 2003).

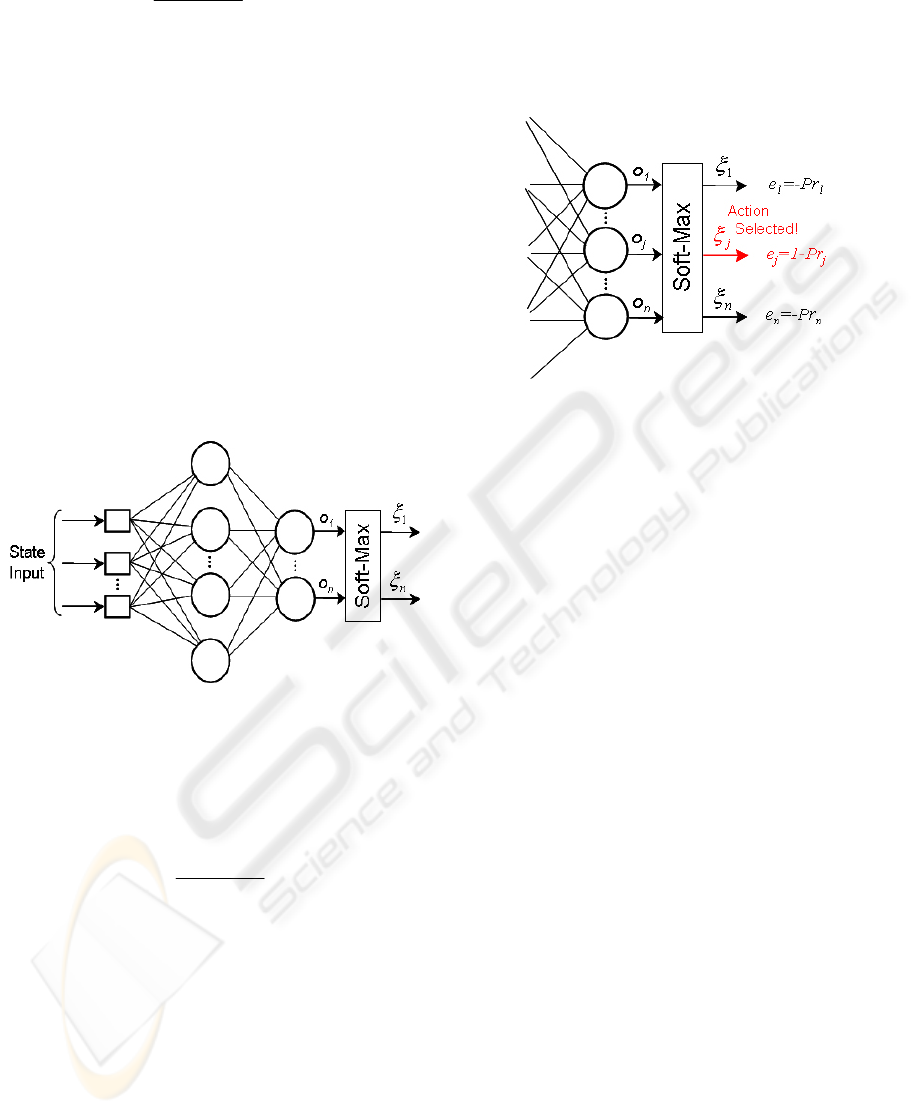
Figure 1: Schema of the ANN architecture used.

After applying the soft-max function, the outputs

of the neural network give a weighting,

(0,1)

∈

each of the vehicle’s thrust combinations. Finally,

the probability of the i

thrust combination is then

given by:

exp( )

∑

(3)

Actions have been labeled with the associated

thrust combination, and they are chosen at random

from this probability distribution.

Once we have computed the output distribution

over the possible control actions, next step is to

calculate the gradient for the action chosen by

applying the chain rule; the whole expression is

implemented similarly to error back propagation

(Haykin

, 1999). Before computing the gradient, the

error on the neurons of the output layer must be

calculated. This error is given by expression (4).

−

(4)

The desired output

will be equal to 1 if the action

selected was

and 0 otherwise (see Fig. 2).

Figure 2: Soft-Max error computation for every output.

With the soft-max output error calculation

completed, next phase consists in computing the

gradient at the output of the ANN and back

propagate it to the rest of the neurons of the hidden

layers. For a local neuron j located in the output

layer we may express the local gradient for neuron j

as:

·()

jjjj

δϕ

(5)

Where

is the soft-max error at the output of

neuron j,

()

corresponds to the derivative of the

activation function associated with that neuron and

o is the function signal at the output for that

neuron. So we do not back propagate the gradient of

an error measure, but instead we back propagate the

soft-max gradient of this error. Therefore, for a

neuron j located in a hidden layer the local gradient

is defined as follows:

()

jjj kkj

δϕ δ

∑

(6)

When computing the gradient of a hidden-layer

neuron, the previously obtained gradient of the

following layers must be back propagated. In (6) the

term

()

represents de derivative of the

activation function associated to that neuron,

the function signal at the output for that neuron and

finally the summation term includes the different

gradients of the following neurons back propagated

DIRECT GRADIENT-BASED REINFORCEMENT LEARNING FOR ROBOT BEHAVIOR LEARNING

227

by multiplying each gradient to its corresponding

weighting (see Fig. 3).

Figure 3: Gradient computation for a hidden-layer neuron.

Having all local gradients of the all neurons

calculated, the expression in (2) can be obtained and

finally, the old parameters are updated following the

expression:

111

()

tt tt

ri z

θγ

+++

=+ (7)

The vector of parameters

represents the

network weights to be updated,

()

is the reward

given to the learner at every time step,

describes

the estimated gradients mentioned before and at last

we have

as the learning rate of the RLDPS

algorithm.

3 CASE TO STUDY: TARGET

FOLLOWING

The following lines are going to describe the

different elements that take place in our problem.

First, the simulated world will be detailed, in a

second place we will present the underwater vehicle

URIS and its model used in our simulation. At last, a

description of the neural-network controller is

presented.

3.1 The World

As mentioned before, the problem deals with the

simulated model of the AUV URIS navigating a

two-dimensional world constrained in a plane region

without boundaries. The vehicle can be controlled in

two degrees of freedom (DOFs), surge (X

movement) and yaw (rotation respect z-axis) by

applying 4 different control actions: a force in either

the positive or negative surge direction, and another

force in either the positive or negative yaw rotation.

The simulated robot was given a reward of 0 if the

vehicle reaches the objective position (if the robot

enters inside a circle of 1 unit radius, the target is

considered reached) and a reward equal to -1 in all

other states. To encourage the controller to learn to

navigate the robot to the target independently of the

starting state, the AUV position was reset every 50

(simulated) seconds to a random location in x and y

between [-20, 20], and at the same time target

position was set to a random location within the

same boundaries. The sample time is set to 0.1

seconds.

3.2 URIS AUV Description

The Autonomous Underwater Vehicle URIS (Fig. 4)

is an experimental robot developed at the University

of Girona with the aim of building a small-sized

UUV. The hull is composed of a stainless steel

sphere with a diameter of 350mm, designed to

withstand pressures of 4 atmospheres (30m. depth).

Figure 4: (Left) URIS in experimental test. (Right) Robot

reference frame.

The experiments carried out use the

mathematical model of URIS computed by means of

parameter identification methods (Ridao et al.,

2004). The whole model has been adapted to the

problem so the hydrodinamic equation of motion of

an underwater vehicle with 6 DOFs (Fossen, 1994)

)has been uncoupled and reduced to modellate a

robot with two DOFs. Let us consider the dynamic

equation for the surge and yaw DOFs:

(8)

(9)

·· · ·

··

()()()()

uu u u

mX mX mX mX

γα β δ

=−−+

−− − −

4243 1 42 43 1424314243

·· · ·

··

()()()()

rr r r

mN mN mN mN

γα β δ

=− − +

−− − −

4243142431424314243

ICINCO 2005 - ROBOTICS AND AUTOMATION

228

Then, due to identification procedure (Ridao et al.,

2004), expressions in (8) and (9) can be rewritten as

follows:

xxxxxxx

vvvv

βγτδ

•

=+ ++

(10)

vvvv

ψψ ψψ ψ ψψ ψ

βγτδ

•

=+ ++

(11)

Where

and v

represent de acceleration in both

surge and yaw DOFs,

v is the linear velocity in

surge and

is the angular velocity in yaw DOF.

The force and torque excerted by the thrusters in

both DOFs are indicated as

and

. The model

parameters for both DOFs are stated as follows:

and

coeficients refer to the linear and the

quadratic damping forces,

represent a mass

coeficient and the bias term is introduced by

. The

identified parameters values of the model are

indicated in Table 2.

Table 2: URIS Model Parameters for Surge and Yaw

Units

Surge

Yaw

-0.3222

1.2426

0.0184

0.5173

0.0012

-0.050

3.3 The Controller

A one-hidden-layer neural-network with 4 input

nodes, 3 hidden nodes and 4 output nodes has been

used to generate a stochastic policy. One of the

inputs corresponds to the distance between the

vehicle and the target location, another one

represents the yaw difference between the vehicle’s

current heading and the desired heading to reach the

objective position. The other two inputs represent

the derivatives of the distance and yaw difference at

the current time-step. Each hidden and output layer

has the usual additional bias term. The activation

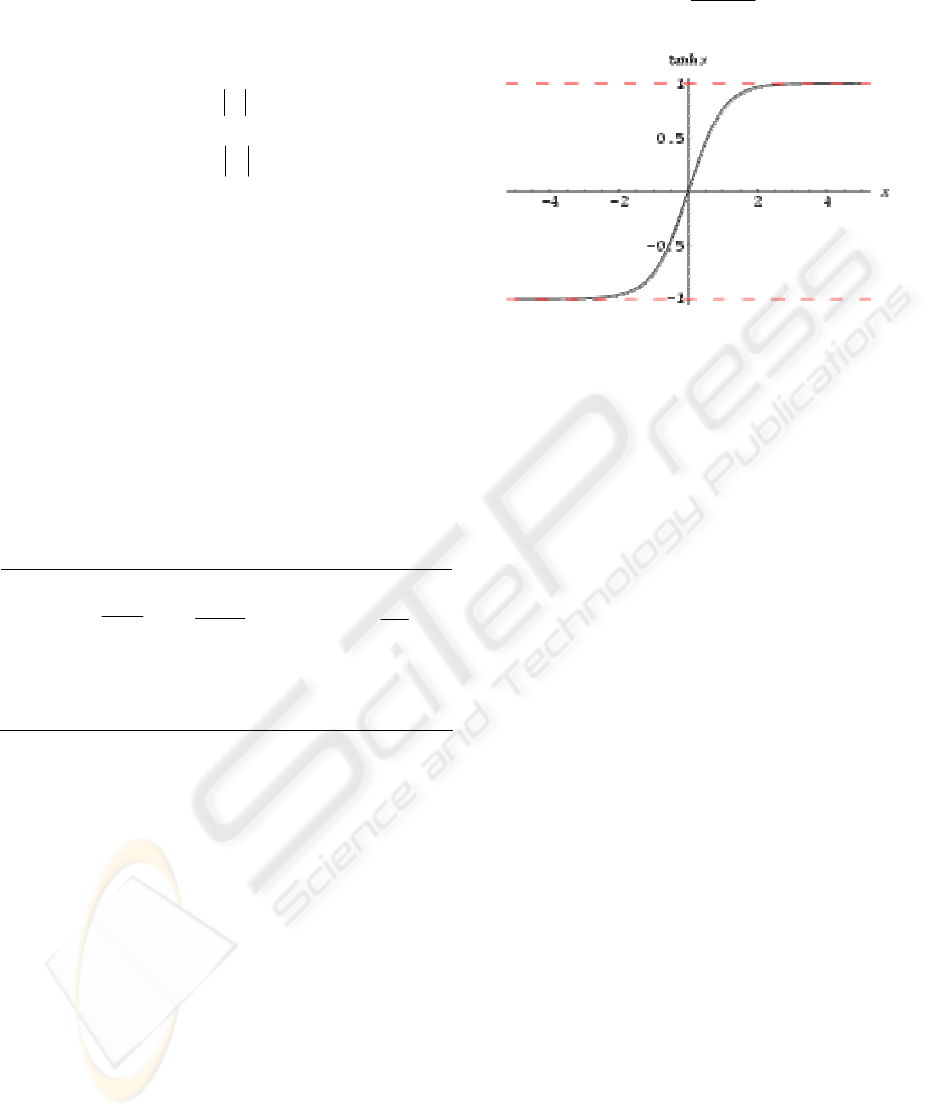
function used for the neurons of the hidden layer is

the hyperbolic tangent type (12, Fig. 5), while the

output layer nodes are linear. The four output

neurons have been exponentiated and normalized as

explained in section 2 to produce a probability

distribution. Control actions are selected at random

from this distribution.

sinh( )

tanh( )

cosh( )

(12)

Figure 5: The hyperbolic tangent function.

4 SIMULATED RESULTS

The controller was trained, as commmented in

section 3, in an episodic task. Robot and target

positions are reseted every 50 seconds so the total

amount of reward per episode percieved varies

depending on the episode. Even though the results

presented have been obtained as explained in section

3, in order to clarify the graphical results of time

convergence of the algorithm, for the plots below

some constrains have been applied to the simulator:

Target initial position is fixed to (0,0) and robot

initial location has been set to four random locations,

20x

and

20y

, therefore, the total amount

per episode when converged to minima will be the

same.

The number of episodes to be done has been set

to 100.000. For every episode, the total amount of

reward percieved is calculated. Figure 6 represents

the performance of the neural-network vehicle

controller as a function of the number of episodes,

when trained using OLPOMDP. The episodes have

been averaged over bins of 50 episodes. The

experiment has been repeated in 100 independent

runs, and the results presented are a mean over these

runs.

The simulated experiments have been repeated

and compared for different values of

and

−

⎛⎞

⎜⎟

⎝⎠

⎛⎞

⎜⎟

⎝⎠

⎛⎞

⎜⎟

⎝⎠

DIRECT GRADIENT-BASED REINFORCEMENT LEARNING FOR ROBOT BEHAVIOR LEARNING

229

For

0.000001

0 200 400 600 800 1000 1200 1400 1600 1800 2000

-500

-450

-400

-350

-300

-250

-200

-150

-100

Total R per Episode, Averaged over bins of 50 Episodes (Alfa 0.000001)

Groups of 50 Episodes

Mean Total R per Episode

beta 0.999

beta 0.99

beta 0.97

Figure 6: Performance of the neural-network puck

controller as a function of the number of episodes.

Performance estimates were generated by simulating

100.000 episodes, and averaging them over bins of 50

episodes. Process repeated in 100 independent runs. The

results are a mean of these runs. Fixed

0.000001

, for

different values of

0.999

0.99

and

0.97

For

0.00001

0 200 400 600 800 1000 1200 1400 1600 1800 2000

-500

-450

-400

-350

-300

-250

-200

-150

-100

-50

Total R per Episode, Averaged over bins of 50 Episodes (Alfa 0.00001)

Groups of 50 Episodes

Mean Total R per Episode

beta 0.999

beta 0.99

beta 0.97

Figure 7: Performance of the neural-network puck

controller as a function of the number of episodes.

Performance estimates were generatedby simulating

100.000 episodes, and averaging them over bins of 50

episodes. Process repeated in 100 independent runs. The

results are a mean of these runs. Fixed

0.00001

, for

different values of

0.999

0.99

and

0.97

For

0.0001

0 200 400 600 800 1000 1200 1400 1600 1800 2000

-500

-450

-400

-350

-300

-250

-200

-150

-100

Total R per Episode, Averaged over bins of 50 Episodes (alfa 0.0001)

Groups of 50 Episodes

Mean Total R per Episode

beta 0.999

beta 0.99

beta 0.97

Figure 8: Performance of the neural-network puck

controller as a function of the number of episodes.

Performance estimates were generatedby simulating

100.000 episodes, and averaging them over bins of 50

episodes. Process repeated in 100 independent runs. The

results are a mean of these runs. Fixed

0.0001

, for

different values of

0.999

0.99

and

0.97

As it can bee apreciated in the figure above

(see Fig. 7), the optimal performance (within the

neural network controller used here) is around -100

for this simulated problem, due to the fact that the

puck and target locations are reset every 50 seconds

and for this reason the vehicle must be away from

target a fraction of the time. The best results are

obtained when

0.00001

and

0.999

, see Fig. 7.

Figure 9 represents the behavior of the trained

robot controller. For the purpose of the illustration,

only target location has been reseted to random

location, not the robot location.

-100 -80 -60 -40 -20 0 20 40 60 80

-100

-80

-60

-40

-20

INITIAL URIS POSITION

FINAL URIS POSITION

Target Following Task,Results After Learning

X Location

Y Location

URIS Trajectory

Target Positions

Figure 9: Behavior of a trained robot controller, results of

target following task asfter learning period is completed.

ICINCO 2005 - ROBOTICS AND AUTOMATION

230

5 CONCLUSIONS

An on-line direct policy search algorithm for AUV

control based on Baxter and Bartlett’s direct-gradient

algorithm OLPOMDP has been proposed. The method

has been applied to a real learning control system in

which a simulated model of the AUV URIS navigates a

two-dimensional world in a target following task. The

policy is represented by a neural network whose input is

a representation of the state, whose output is action

selection probabilities, and whose weights are the policy

parameters. The objective of the agent was to compute a

stochastic policy, which assigns a probability over each

of the four possible control actions.

Results obtained confirm some of the ideas

presented in section 1. The algorithm is easier to

implement compared with other RL methodologies like

value function algorithms and it represents a

considerable reduction of the computational time of the

algorithm. On the other side, simulated results show a

poor speed of convergence towards minimal solution.

In order to validate the performance of the

method proposed, future experiments are centered

on obtaining empirical results: the algorithm must be

tested on real URIS in a real environment. Previous

investigations carried on in our laboratory with RL

value functions methods with the same prototype

URIS (Carreras et al., 2003) will allow us to

compare both results. At the same time, the work is

focused in the development of a methodology to

decrease the convergence time of the RLDPS

algorithm.

ACKNOWLEDGMENTS

This research was esponsored by the spanish

commission MCYT (DPI2001-2311-C03-01). I

would like to give my special thanks to Mr. Douglas

Alexander Aberdeen of the Australian National

University for his help.

REFERENCES

R. Sutton and A. Barto, Reinforcement Learning, an

Introduction. MIT Press, 1998.

W.D. Smart and L.P Kaelbling, “Practical reinforcement

learning in continuous spaces”, International

Conference on Machine Learning, 2000.

N. Hernandez and S. Mahadevan, “Hierarchical memory-

based reinforcement learning”, Fifteenth International

Conference on Neural Information Processing

Systems, Denver, USA, 2000.

D.P. Bertsekas and J.N. Tsitsiklis, Neuro-Dynamic

Programming. Athena Scientific, 1996.

R. Sutton, D. McAllester, S. Singh and Y. Mansour,

“Policy gradient methods for reinforcement learning

with function approximation” in Advances in Neural

Information Processing Systems 12, pp. 1057-1063,

MIT Press, 2000.

C. Anderson, “Approximating a policy can be easier than

approximating a value function” Computer Science

Technical Report, CS-00-101, February 10, 2000.

R. Williams, “Simple statistical gradient-following

algorithms for connectionist reinforcement learning”

in Machine Learning, 8, pp. 229-256, 1992.

J. Baxter and P.L. Bartlett, “Direct gradient-based

reinforcement learning” IEEE International

Symposium on Circuits and Systems, May 28-31,

Geneva, Switzerland, 2000.

V.R. Konda and J.N. Tsitsiklis, “On actor-critic

algorithms”, in SIAM Journal on Control and

Optimization, vol. 42, No. 4, pp. 1143-1166, 2003.

S.P. Singh, T. Jaakkola and M.I. Jordan, “Learning

without state-estimation in partially observable

Markovian decision processes”, in Proceedings of the

International Conference on Machine Learning,

pp. 284-292, 1994.

N. Meuleau, L. Peshkin and K. Kim, “Exploration in

gradient-based reinforcement learning”, Technical

report AI Memo 2001-003, April 3, 2001.

J. Baxter and P.L. Bartlett, “Direct gradient-based

reinforcement learning I: Gradient estimation algorithms”

Technical Report. Australian National University, 1999.

P. Ridao, A. Tiano, A. El-Fakdi, M. Carreras and A.

Zirilli, “On the identification of non-linear models of

unmanned underwater vehicles” in Control

Engineering Practice, vol. 12, pp. 1483-1499, 2004.

D. A., Aberdeen, Policy Gradient Algorithms for Partially

Observable Markov Decision Processes, PhD Thesis,

Australian National University, 2003.

S. Haykin, Neural Networks, a comprehensive foundation,

Prentice Hall, Upper Saddle River, New Jersey, USA,

1999.

T.I., Fossen, Guidance and Control of Ocean Vehicles,

John Wiley and Sons, New York, USA, 1994.

J. A. Bagnell and J. G. Schneider, “Autonomous

Helicopter Control using Reinforcement Learning

Policy Search Methods”, in Proceedings of the IEEE

International Conference on Robotics and Automation

(ICRA), Seoul, Korea, 2001.

M. T. Rosenstein and A. G. Barto, “Robot Weightlifting

by Direct Policy Search”, in Proceedings of the

International Joint Conference on Artificial

Intelligence, 2001.

N. Kohl and P. Stone, “Policy Gradient Reinforcement

Learning for Fast Quadrupedal Locomotion”, in

Proceedings of the IEEE International Conference on

Robotics and Automation (ICRA), 2004.

M. Carreras, P. Ridao and A. El-Fakdi, “Semi-Online

Neural-Q-Learning for Real-Time Robot Learning”, in

Proceedings of the IEEE/RSJ International

Conference on Intelligent Robots and Systems (IROS),

Las Vegas, USA, 2003.

DIRECT GRADIENT-BASED REINFORCEMENT LEARNING FOR ROBOT BEHAVIOR LEARNING

231