WHEN SHOULD THE NON LINEAR CAMERA CALIBRATION

BE CONSIDERED?

Carlos Ricolfe-Viala, Antonio-José Sánchez-Salmerón

Department od Systems Engineering and Automatic Control, Polytechnic University of Valencia, Camino de Vera s/n,

Valencia,Spain

Keywords: Parameter estimation, non linear techniques, camera calibration.

Abstract: In 3D modelling reconstruction of points, lines, planes or conics are done in the virtual 3D space. Their

situations in the 3D virtual scene are defined by the situation of the recognized features in one or several

images. Estimation of a parameter vector which models the object is carried out starting with recognized

features in the image. Since positions of recognized features in the image are contaminated with noise the

solution for the parameter vector is not exact. In order to obtain “the best” solution, optimization algorithms

which reduce a residual error are used. They can be classified into linear and non linear ones.The aim of this

paper is to determine the quality of estimated parameters if no linear estimation process is utilized. It is

shown that in some cases non linear optimization algorithms diverges and worst parameters are computed

using non linear methods. In order to obtain experimental results, camera parameters have been estimated

under different conditions.

1 INTRODUCTION

Computer vision is a branch of artificial intelligence

and image processing concerned with computer

processing of images from the real world. Computer

vision typically requires a combination of low level

image processing to enhance the image quality (e.g.

remove noise, increase contrast) and higher level

pattern recognition and image understanding to

recognise features present in the image. In cases of

3D modelling, reconstruction of points, lines, planes

or conics are done in the virtual 3D space. Their

situations in the 3D virtual scene are defined by the

situation of the recognized features in one or several

images. In this category, equations that relate the

parameters to be estimated with the coordinates of

the features in the images are established. Therefore,

estimation of the parameter vector is carried out

starting with recognized features in the image. Since

positions of recognized features in the image are

contaminated with noise the solution for the

parameter vector is not exact. In order to obtain “the

best” solution, optimization algorithms are used.

Optimization algorithms can be classified into linear

or non linear one.

Linear algorithms provides a close form solution for

“the best” parameter vector which fits with a given

set of recognized features in the image. The

parameter set can be computed by solving linear

equations. Since no iterations are required, the

solution is computed faster. However, such methods

have two disadvantages. First, if non linear relation

exists between image features and parameters, they

can not be computed and second, if the parameters

satisfy some restriction, it is not guaranteed than the

computed ones succeed it.

Non linear optimization methods involve using an

iterative algorithm with the objective of minimizing

residual errors of some index. The advantage of this

type of technique is that the parameter estimation

can cover non linear relation between the feature

positions in the image and the parameters. Another

advantage is that the algorithm may achieve high

accuracy, provided that the estimation model is

good, and correct convergence has been reached.

However, since the algorithm is iterative, the

procedure may end up with a bad solution unless a

good initial guess is available. Furthermore, non

linear relation included in the parameter space may

result in a unstable minimization if the procedure of

iterations is not properly designed. The iteration can

lead to divergence or false solutions.

Two step optimization methods seem to be most

useful. Parameters which accomplish linear relation

are computed first with a close form solution and

afterwards, they a used as initial guess to improve

237

Ricolfe-Viala C. and Sánchez-Salmerón A. (2005).

WHEN SHOULD THE NON LINEAR CAMERA CALIBRATION BE CONSIDERED?.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 237-242

DOI: 10.5220/0001189702370242

 SciTePress

them and estimate the remaining parameters.

Iterative schemes also use one set of parameters to

estimate a second set of parameters which improves

the first one. This is done iteratively until a threshold

value of the residual error is achieved. The

advantage of this method is that a closed form

solution is derived for most for parameters and the

number of parameters to be estimated through

iterations is relatively small.

In this paper, an evaluation of the non linear

parameter estimation method is carried out in order

to define the conditions in which it works right.

First, a small presentation of camera calibration

method using a 3D pattern is done. Depending on

the index to minimize the solution can differ.

Second, an evaluation of different kinds of residual

error is carried out. All this errors are combined in

different situations and an estimation of the

evolution of the non linear estimation algorithm is

done. It is shown that in some situations the non

linear estimation algorithm diverges and false

solutions can be computed. Finally, experimental

results are shown. In this case the camera parameters

are estimated. Experimental results back what it has

been presented in the paper.

2 NON LINEAR CAMERA

CALIBRATION

Camera calibration process estimates the relation

between the points coordinates in the pattern and its

correspondence in the image. This relation is defined

with the camera features and its localization in the

scene. A linear relation exists if camera distortion is

not considered. It is expressed with the following

expression

=(u

) are the points coordinates in the image,

=(x

, z

) are its correspondences in the pattern

and m

are the elements of the projection matrix M.

The projection matrix is formed with the camera

features and its location in the world (Faugeras

1993). The aim is to compute M starting with the

points coordinates. Several methods exist (Hartley

2000)(Heikkilä 1997). First a linear estimation of

camera parameters is carried out and after a non

linear adjustment is done. Non linear adjustment is

done including non liner relation of point’s

coordinates (Faugeras 1993). Since points

coordinates are corrupted with noise, no exact

solution will be achieve. The computed solution is

the best one which satisfies given data. In the

following the noisy data will be denoted with q’ and

p’.

2.1 Geometrical error

For an estimated projection matrix M* a geometrical

error e can be defined. This geometrical error is the

sum of the Euclidean distance between the measured

coordinate’s q’ of the points in the image and the

result of projecting the 3D pattern p’ in the image

with the estimated matrix M*. In this case q*

denotes the optimal image coordinates of the

measured points, according to the estimated camera

parameters.

∑

’-M*p’

∑

’-q*

Depending on the method utilized to compute the

projection matrix M*, the accuracy of the estimated

parameters with the given data is better. In the

following section a classification of linear and non

linear method is done according to this geometrical

error.

3 WHEN DOES THE NON

LINEAR CAMERA

CALIBRATION BE

CONSIDERED?

Until now, all the effort goes to improve the

estimation of the camera model parameters. This

improvement is based in the minimization of the

Euclidean distance between the measured points’

coordinates q’ and the ones q* computed from an

estimation of the camera parameters M*. Starting

parameters have been computed with linear methods

which compute them using a close form solution.

From an algebraic point of view, the result is correct

but geometrically it could be absurd, since this error

has no physical meaning. Parameters from the

closed form solution are improved to obtain best

fitting parameters which reduce the geometrical

error. This means that the non linear estimation

obtains a set of parameters with less geometrical

error that those obtained with linear methods. This

geometrical error is always regarding to the noisy

measure of the points coordinates q’ and p’. In fact,

there is a set of noisy points used to accomplish the

estimation process q’ and p’, and there is another set

of ideal points without noise q and p which are

always unknown. In theory, if this set of ideal

point’s q and p were used in the estimation process,

exact values of the model parameters will be

()

⎥

⎦

⎤

⎢

⎣

⎡

+++

⎥

⎦

⎤

⎢

⎣

⎡

34333231

24232221

34333231

14131211

3411

,....,

mzmymxm

mmf

iii

ICINCO 2005 - ROBOTICS AND AUTOMATION

238

computed. Due to the noise in the measured points

coordinates, these ideal points are always unknown.

That is why it is impossible to obtain the exact

camera model parameters in any case.

If the estimated parameters are arranged in a line

according to the geometrical error they generate,

several situations arise. The residual geometrical

error of the noise points with respect to themselves

is always cero e

=0. The geometrical error of the

ideal points q and p regarding to the noisy points q’

and p’ is always an unknown value called e

Additionally, there are geometrical errors with the

set of points generated with the parameters estimated

with linear methods and the parameters estimated

with non linear methods. These are called e

, e

respectively. These errors are always known and

they will be bigger than the geometrical error cero

. Moreover, since the set of points resulting from

the non linear estimation has less geometrical error,

will be always on the left side of e

. Now, the

essential question is, where is the unknown e

?. The

situation of this unknown, give us the efficiency of

the non linear estimation regarding the linear one. If

the exact parameters are those which generate a set

of points with a geometrical error e

, the goal is to

compute a set of parameters which generate a set of

points with a geometrical error close to the unknown

. Several situations showed in figure 1 arise.

In case A, better parameters will be always

obtained using non linear estimation. In this case,

since e

is on the left side of e

, with the non linear

estimation better results will be obtained. In the case

B, since e

is on the right side of e

, with the non

linear finding worse camera parameters will be

computed. In the case C, the value of e

is between

and e

. In this case, better results with the non

linear method will be obtained if e

is closer to e

Since it is impossible to know the ideal points and

therefore e

, it is impossible to know if better results

will be obtained with the non linear method.

However, although it is impossible to know the

set of ideal points which give e

, it is possible to

know the noise level of the point’s coordinates. This

noise level gives the separation between e

and e

. If

the noise level is elevated, e

will be far from e

Otherwise, if the noise level is small, these values

will be closer. In the case of elevated level of noise,

the probability of obtaining a geometric error e

situated is case B is very high since e

and e

are

much separated. The set of parameters computed

with the non linear method generates points which

are closer of the noisy points. This means that the

estimation is worse although the residual

geometrical error is smaller. Therefore, with

elevated noise level it is more probably to obtain

worse results if the non linear method is used. From

the finding algorithm point of view, if the noise level

is high, the starting values of the parameters are far

from the ideal ones. This means that the finding

algorithm is unable to achieve the absolute minimum

and it is deviated to local one. This local minimum

gives worse values of the parameters although the

geometrical error is small. Otherwise if the noise

level is small, e

is closer to e

. Consequently, the

probability of e

is higher in the case A. In this case

the parameters computed with the non linear method

are better. The finding algorithm reduces the

geometrical error and it is closer to the ideal one.

Since the starting values of the parameters are close

to the ideal one, the finding algorithm stops close to

the absolute minimum.

The question now is how do we decide if use or

not non linear parameter estimation? The decision

should be based on the noise level of the

measurements of the points coordinates. Taking into

account that most of geometric computation

problems are χ

variables with r degrees of freedom,

where r depends on the application, it is possible to

know the noise level of the features coordinates.

This noise level ε

is computed knowing the residual

of the optimization. It is defined as

where I* is the residual of the optimization

(Kanatani 1995). It is necessary also to define the

limit of noise level for which the non linear

estimation deviates form the right solution. It should

be done testing each application. In this paper

camera calibration process has been tested.

In order to obtain better results, a new set of

point’s coordinates should be computed. If the

measured point’s coordinates are corrupted with

noise and the finding algorithm tries to satisfy it,

worse results will be obtained. Therefore, if a new

set of point’s coordinates with smaller level of noise

is satisfied, better results will be obtained.

Figure 1: Estimation methods arranged in a line, based on

their residual geometrical errors

I *

WHEN SHOULD THE NON LINEAR CAMERA CALIBRATION BE CONSIDERED?

239

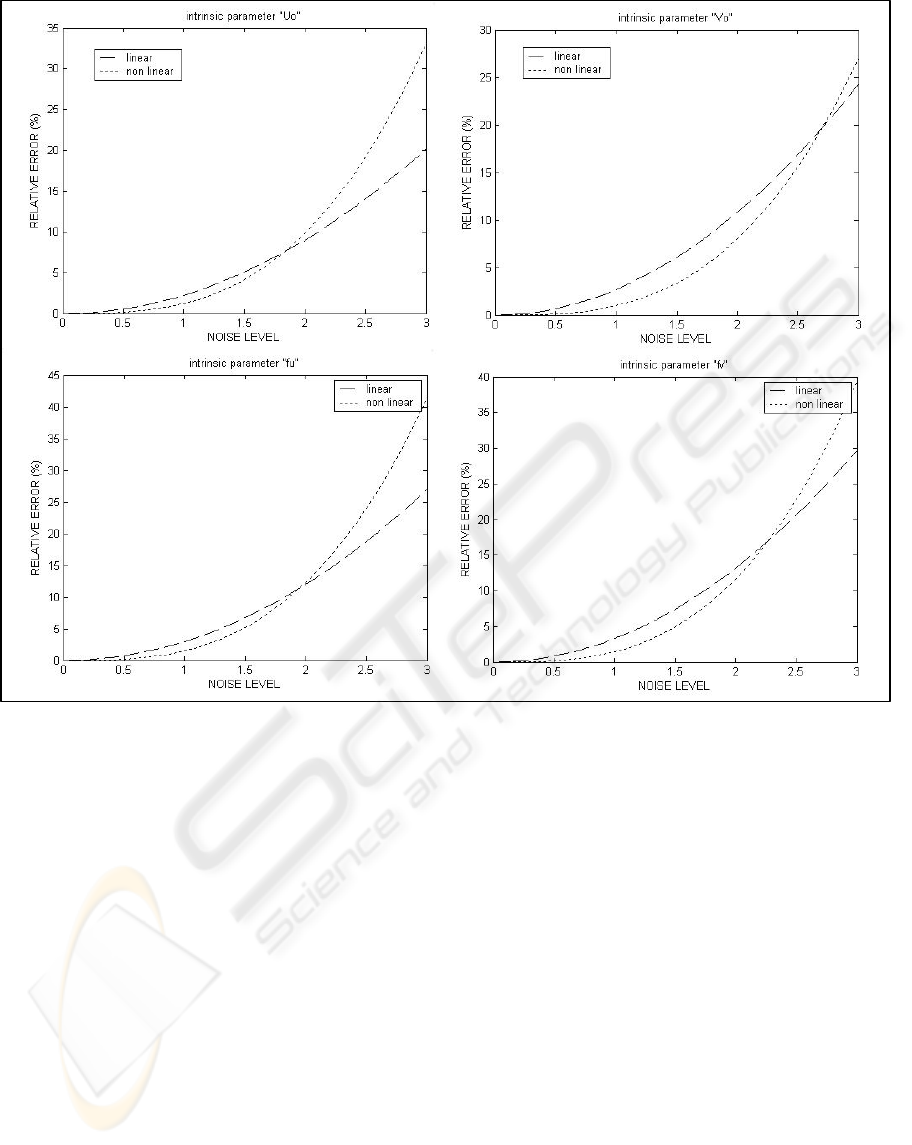
Figure 2: Relative error of estimated internal camera parameters

4 EXPERIMENTAL RESULTS

Both, simulated and real experiments have been

done to test the performance of the optimization

algorithms. First, calibration process with non linear

algorithms is tested with synthetic data to extract

conclusions about the influence of the noise level in

the computed parameters. Second, the overall

procedure is tested with real data provided with the

images o calibration template. This second series of

experiments demonstrates the validity of the overall

deduction.

4.1 Simulated experiments with

synthetic data

Several situations have been simulated in order to

extract some conclusion about non linear calibration

technique. A lot of different number of points of

interest has been used. This feature has no

significant effect on the estimated results from the

point of view of deviation of the non linear

parameters estimation. Finally, a set of 50 points in

the scene arranged into two planes has been used.

The camera is situated 1 m away form the Y axis,

with an angle of incidence of the camera optical axe

of 45 degrees with the X-Y plane. The starting

values of the parameters are computed with the

Direct Linear Transformation (DLT) algorithm

(Hartley 2000). A priori, no camera intrinsic

parameters are known. The non linear cost function

is not critical in order to test the deviation of the non

linear optimization. Similar results have been

computed. Depending on the used cost function, one

restriction or another is satisfied. Cost functions

which include the restriction of the camera

projection matrix have similar behaviour. The noise

level in the point’s coordinates is the only feature

which has a lot of effect in the estimated camera

parameters. The results are shown in figure 2. In this

experiment the noise level changes from 0 to 3

pixels in the image coordinate points and from 0 to 3

ICINCO 2005 - ROBOTICS AND AUTOMATION

240

mm in the 3D scene coordinate points. Steps of 0.1

have been taken. A set of points in the 3D scene

arranged into two planes is used and a camera ideal

model is generated with a set of intrinsic and

extrinsic parameters. This ideal model is represented

in a projection matrix which is used to calculate the

projections in the image of the 3D points in the

scene. Both sets of point’s coordinates (image and

scene) are corrupted with Gaussian noise. This

corrupted data is used to compute the camera

parameters, starting with the linear method and

finishing with the non linear one. This process is

done 100 times per step. After 100 times, the mean

of the estimated parameters with the linear method

and the non linear one are computed. Figure 2 shows

the result for each level of noise. It shows the

relative error for each value of the camera

parameters. The continuous line shows the linear

estimation and the dotted line is the non linear one.

In this case, non linear estimation is done without

any restriction included into the index. Results show

that, non linear calibration method can not improve

the results of the linear one, if the noise level is too

high. This result demonstrates the bad performance

of the non linear camera calibration method if the

noise level is high.

The term “to improve the results” should not be

interpreted as to reduce the geometrical error. It is

true that the non linear camera calibration method

reduces the geometrical error but from a practical

point of view, this method computes worse values of

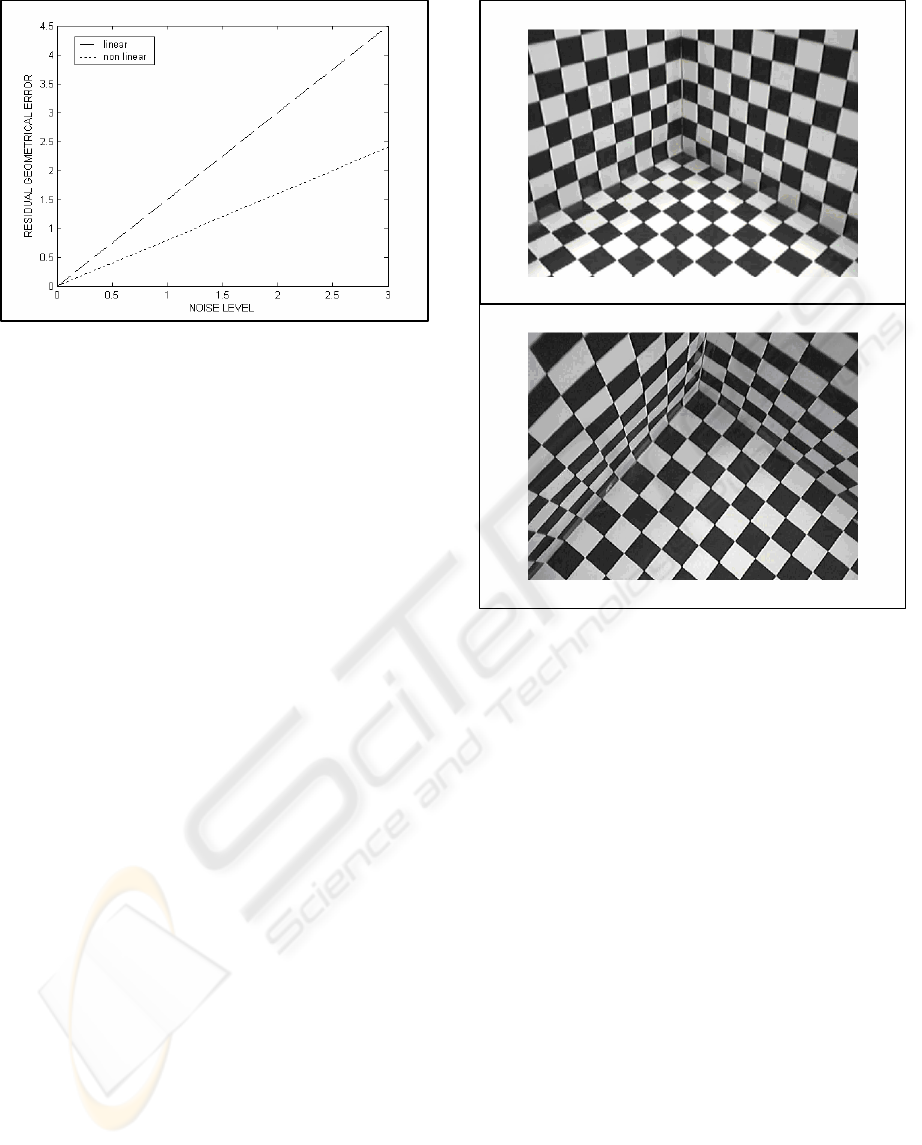
the absolute camera model parameters. Figure 3

shows the residual optimization using linear and non

linear optimization method. It is clear that the non

linear optimization method reduces the geometrical

error a lot, but when the noise level is high, this

reduction does not improve the absolute values of

the parameters.

Seeing the figures, the noise level from which the

non linear optimization method computes worst

results is about 2.1.

4.2 Experiments with real images

From the point of view of calibration of a real

camera, images from different positions are taken of

a calibration template. Calibration images are shown

in figure 4. Images from different positions are taken

to detect the coordinates of the calibration points

with different accuracy. Then, the noise level of

points coordinates changes. With these points, the

calibration process has been carried out in the same

way as in the simulation stage. Camera has been

calibrated 100 times in order to extract mean values.

Smaller residual optimization has been computed

with non linear optimization techniques. Also,

different parameters have been computed with each

method. Since the real values of camera parameters

are not known it is impossible to decide which

calibration is better. However, the noise level of the

points coordinates computed with the χ

test can

help us to decide. In this case noise level about 2 has

been computed with images 2 and 3 as is shown in

Figure 3: Residual geometrical error with linear and non

linear method

Figure 4: Images of the calibration template

WHEN SHOULD THE NON LINEAR CAMERA CALIBRATION BE CONSIDERED?

241

table 1. Taking into account the simulated results, no

linear optimization method should be discarded or

better detection of the points coordinates in the

image should be done. In this case, better calibration

stage should be used.

Table 1: Results of experiments with real data

Residual optimization

Lineal Non linear

Noise

level ε

Image 1 2.901 1.588 1.224

Image 2 5.687 1.026 2.345

These results can be extrapolated to any

parameter estimation process. It is necessary to take

into account the noise level of the input data before

using non linear optimization techniques.

5 CONCLUSIONS

For parameters estimation, the non linear

optimization method can be useful if the noise level

of the input data is not very high. If the noise level is

too high, the non linear optimization technique

computes worst absolute results. The algorithm

converges to a local minimum which improve the

geometrical error but not absolute values of the

parameters, even using the Levenberg-Marquardt

finding algorithm. Non linear optimization

minimizes a cost function with a lot of degrees of

freedom and it can diverge to false results if the

noise level is very high. In these cases linear

parameter estimation methods are faster and achieve

better results. In order to improve parameter

estimation process using non linear techniques, low

noise input data should be used.

REFERENCES

F. Dornaika and C. Garcia, 1997, Robust camera

calibration using 2D to 3D feature correspondences,

International Symposium SPIE, San Diego.

O. Faugeras, 1993, Three dimensional computer vision,

The MIT Press, Massachusetts.

R. Hartley and A. Zisserman, 2000, Multiple View

geometry in computer vision, Cambridge, United

Kingdom

J. Heikkilä and O. Silven, 1997, A four step camera

calibration procedure with implicit image correction,

IEEE Computer Society Conference on Computer

Vision and Pattern Recognition, San Juan, Puerto Rico.

K. Kanatani, 1995, Statistical optimization for geometric

computation, Springer.

W. Press, B. Flannery, S. Teukolsky, W. Vetterling, 1988,

Numerical recipes in C, Cambridge, United Kingdom.

ICINCO 2005 - ROBOTICS AND AUTOMATION

242