
WAVELET TRANSFORM MOMENTS FOR FEATURE
EXTRACTION FROM TEMPORAL SIGNALS
Ignacio Rodriguez Carreño
Department of Electrical and Electronic Engineering, Public University of Navarre, Arrosadia, Pamplona, Spain
Marko Vuskovic
Department of Computer Science, San Diego State University, San Diego, California, USA
Keywords: Pattern recognition, EMG, feature extraction, wavelets, moments, support vector machines.
Abstract: A new feature extraction metho
d based on five moments applied to three wavelet transform sequences has
been proposed and used in classification of prehensile surface EMG patterns. The new method has essen-
tially extended the Englehart's discrete wavelet transform and wavelet packet transform by introducing more
efficient feature reduction method that also offered better generalization. The approaches were empirically
evaluated on the same set of signals recorded from two real subjects, and by using the same classifier, which
was the Vapnik's support vector machine.
1 INTRODUCTION
The electromyographic signal (EMG), measured at
the surface of the skin, provides valuable informa-
tion about the neuromuscular activity of a muscle
and this has been essential to its application in clini-
cal diagnosis, and as a source for controlling assis-
tive devices, and schemes for functional electrical
stimulation. Its application to control prosthetic
limbs has also presented a great challenge, due to the
complexity of the EMG signals.
An important requirement in this area is to accu-
rately classify d
ifferent EMG patterns for controlling
a prosthetic device. For this reason, effective feature
extraction is a crucial step to improve the accuracy
of pattern classification, therefore many signal rep-
resentations have been suggested.
Various temporal and spectral approaches have
been a
pplied to extract features from these signals. A
comparison of some effective temporal and spectral
approaches is given in (Du & Vuskovic 2004),
where the authors have applied moments to short
time Fourier transform (STFT), and short time
Thompson transform (STTT) on prehensile EMG
patterns.
The wavelet transform-base
d feature extraction
techniques have also been successfully applied with
promising results in EMG pattern recognition by
Englehart and others (1998).
The discrete wavelet transform (DWT) and its
g
eneralization, the wavelet packet transform (WPT),
were elaborated in (Englehart 1989a). These tech-
niques have shown better performance than the oth-
ers in this area because of its multilevel decomposi-
tion with variable trade-off in time and frequency
resolution. The WPT generates a full decomposition
tree in the transform space in which different wave-
let bases can be considered to represent the signal.
The techniques were applied to feature extraction
from surface EMG signals.
However, these techniques produce a large
am
ount of coefficients, since the transform space has
very large dimension. This fact suggests the system-
atic application of feature selection or projection
methods and dimensionality reduction techniques to
enable the methodology for real time applications.
Englehart applied feature selection and feature pro-
jection that yielded better classification results and
improved time efficiency. Specifically, the principal
component analysis (PCA) was used due to its abil-
ity to model linear dependencies and to reject irrele-
vant information in the feature set (Englehart etal.
1999).
This paper continues the work described above
by
taking a different approach to feature reduction.
Extending the idea of spectral moments suggested in
71
Rodriguez Carreño I. and Vuskovic M. (2005).
WAVELET TRANSFORM MOMENTS FOR FEATURE EXTRACTION FROM TEMPORAL SIGNALS.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and
Control, pages 71-78
DOI: 10.5220/0001190100710078
Copyright
c
SciTePress
(Du & Vuskovic 2004) the sequences of wavelet
coefficients are further subjected to the calculation
of their temporal moments. The main goal of this
work is to propose and empirically compare two
different novel feature extraction approaches based
on simple two-scale DWT and WPT with the two
best Englehart’s approaches using the DWT and the
WPT in combination with principal component
analysis (PCA).
In this new approach, the first five raw moments
were applied to DWT transformed prehensile EMG
sequences, which has proven to be very advanta-
geous in the classification stage. The methods em-
ployed a simple DWT or WPT with only three trans-
form sequences, instead of the full DWT or WPT
used by Englehart. This has eliminated the tedious
feature reduction procedures and PCA.
The evaluation of the three approaches was car-
ried out on the same set of data, and with an identi-
cal classifier based on Vapnik's support vector ma-
chines (SVM) with a linear kernel.
2 PREHENSILE EMGS
The research presented here was motivated by the
need for classification of prehensile elec-
tromiographic signals (EMG) for control of a multi-
functional prosthetic hand (Vuskovic etal. 1995).
Since the hand-preshaping phase in an average ob-
ject grasp takes about 500 ms, it is important to ac-
complish the feature extraction and classification in
less than 400 ms, preferably in 200 ms. Such a diffi-
cult task requires very strong feature extractor and
classifier.
The mioelectric control of multifingered hand
prostheses was studied in several papers, for exam-
ple (Nishikava 1991), (Uchida 1992), (Farry 1996),
and (Huang 1999). Most of the ideas in these efforts
were inspired by Hudgins (Hudgins etal. 1991). In
this work the concept of preshaping of multifunc-
tional grasps was based on the recognition of a par-
ticular finger joint movement. In an earlier work
done at San Diego State University, the approach
was rather different, based on grasp types, instead of
hand configurations in joint space. Once a grasp type
is recognized from the recorded EMGs, it can be
then synergistically mapped into the desired joint
configuration (Vuskovic 1995) for any hand, with
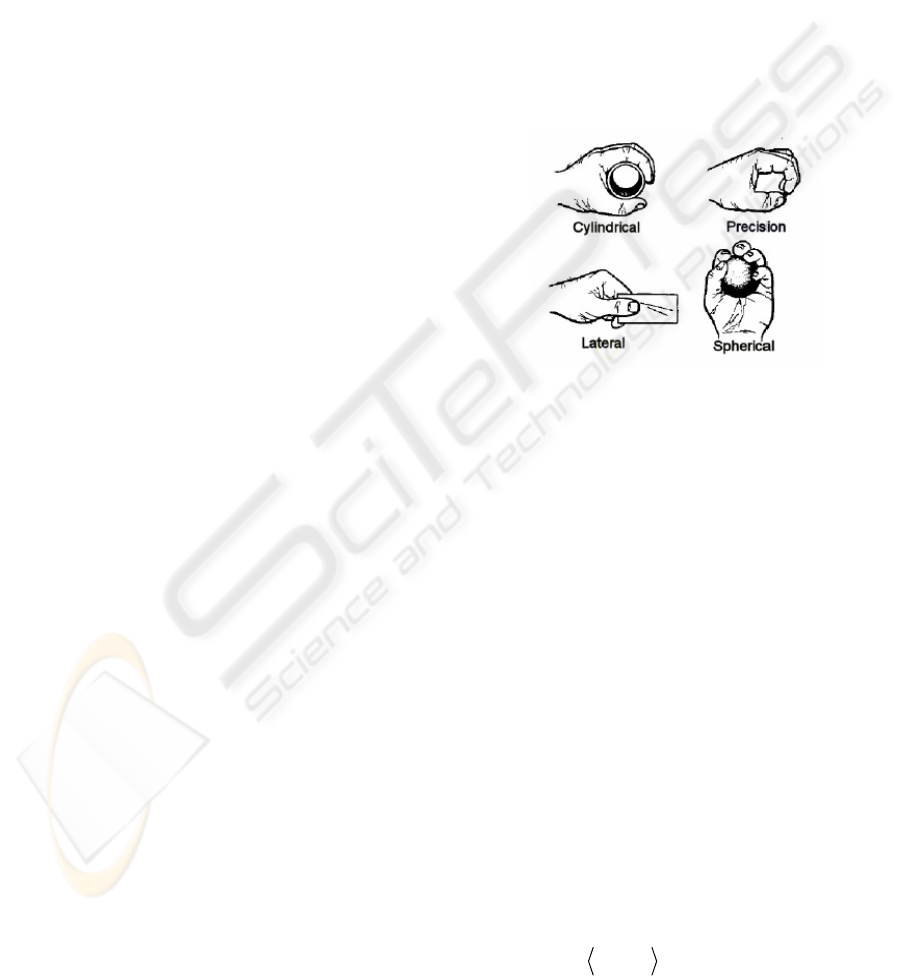
any number of degrees of freedom. We have consid-
ered four basic grasp types according to the
Schlesinger classification (Schlesinger 1919): cylin-
drical grasp (C), spherical grasp (S), lateral grasp (L)
and precision grasp (P), see figure 1.
3 EXPERIMENTAL SETUP
Four-channel surface EMG signals from two healthy
subjects were recorded at 1000 Hz sampling fre-
quency. The recording was done while the subject
has repeatedly performed the four grasp motions.
There were 216 grasp recordings evenly distributed
across the four grasps types: 60 (subject 1) + 4 (sub-
ject 2) for cylindrical grasp, 30+10 for precision
grasp, 30+10 for lateral grasp and 60 + 12 for
spherical grasp. Three different EMG sequence
lengths were used: 200 ms, 300 ms and 400 ms. The
200 and 300 ms sequences were obtained by truncat-
ing the recordings of 400 ms sequences. (The se-
quences of 300 ms were not presented in this paper.)
Figure 1: Four grasp types.
4 DISCRETE WAVELET
TRANSFORM
The DWT is a transformation of the original tempo-
ral signal into a wavelet basis space. The time-
frequency wavelet representation is performed by
repeatedly filtering the signal with a pair of filters
that cut the frequency domain in the middle.
Specifically, the DWT decomposes a signal into
an approximation signal and a detail signal. The
approximation signal is subsequently divided into
new approximation and detail signals. This process
is carried out iteratively producing a set of approxi-
mation signals at different detail levels (scales) and a
final gross approximation of the signal.
The detail Dj and the approximation Aj at level j
can be obtained by filtering the signal with an L-
sample high pass filter g, and an L-sample low pass
filter h. Both approximation and detail signals are
downsampled by a factor of two.
This can be expressed as follows:
1
11
0
[] [] [] [2 ],
L
jj j
k
An A n hkA n k
−
−−
=
==
∑
Η −
(1)
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
72

1
11
0
[] [] [] [2 ],
L
jj j
k
Dn D n gkA n k
−
−−
=
==
∑
G −
(2)
where
0
, n = 0,1,…N-1 is the original temporal
sequence, while H and G represent the convolu-
tion/down sampling operators. Sequences g[n] and
h[n] are associated with wavelet function
[]An
()
ψ
t and
the scaling function
through inner products: ()ϕ t
[] (),2 (2 ),gn t t n=ψ ψ −
(3)
[] (),2(2 ).hn t t n=ϕ ϕ −
(4)
Operators H and G can be applied repeatedly in al-
teration, for example:
0
AA A= HH
, DD =
0
A= GG ,
AD =
0
AGH ,
DA =
0
The A and D sequences obtained as the result of
DWT are still massive in terms of the number of
samples, which contributes to large dimensionality of
feature space. Besides, the sequences have a high
noise component inherited from the original EMG
signal.
A= HG
, etc.
A feature extraction approach based on DWT
applied by Englehart (1998, 1998a) consists of four
differentiated phases:
1. Perform full DWT decomposition of the EMG
signals, until scale j = log2 (N), with the Coiflet
wavelet of order 4 (C4);
2. Square the DWT coefficients;
3. Apply PCA for dimensionality reduction tech-
niques;
4. Determine the optimal number of features per
channel based on the target classifier.
An optimization phase is needed before selecting the
adequate number of PCA features in order to maxi-
mize the performance of the target classifier. The
optimum number of features was 100 DWT coeffi-
cients per channel of the EMG signal used in this
work.
5 WAVELET PACKET
TRANSFORM
The WPT is a generalization of DWT. It generates a
full wavelet basis decomposition tree. In each scale,
not only the approximation signal as in DWT, but
also the detail signals are filtered to obtain another
two low and high frequency signals. Many different
representations of a signal can be obtained by select-
ing different wavelet packet basis. In this regard
WPT is superior to DWT, as the chosen basis can be
optimized with respect to frequency or time resolu-
tion.
Englehart (1999) generated a feature extraction
method based on the WPT for EMG signals. In this
method a previous phase must be applied to the set
of training signals. The underlying idea is to select
the WPT basis that best classifies all classes of sig-
nals. For this purpose, Englehart proposed a modi-
fied version of the local discriminant basis (LDB)
algorithm (Englehart 1998a, 2001), to maximize the
discrimination ability of the WPT by using a class
separability cost function (Saito & Coifman 1995).
Once the best basis for classification is defined (for
different channels and different signal lengths), the
following steps must be performed:
1. Perform the full WPT decomposition until
scale j = log
2
(N), with the Symlet wavelet of
order 5 (S5);
2. Square the WPT coefficients;
3. Average energy maps within each subband;
4. Select the WPT coefficients from a basis cho-
sen previously for each channel and for differ-
ent signal lengths;
5. Extract the optimal number of features based
on the target classifier;
6. Apply PCA transform to the feature space for
dimensionality reduction (removing the eigen-
vectors whose eigenvalues are zero);
7. Extract the optimum number of features per
channel for the target classifier;
The optimal number of features for Englehart’s
WPT based approach and for the support vector ma-
chine as the target classifier (see section 7) was
found to be three features per channel, per signal
length.
6 DWT AND WPT MOMENTS
1
The new approach for feature extraction presented
here is based on DWT and WPT, and on the calcula-
tion of their temporal moments. The approach was
first proposed in (Rodriguez & Vuskovic 2005) as an
extension of the idea of spectral moments (Du &
Vuskovic 2004).
Specifically, we used two different wavelets suc-
cessfully applied by Englehart on surface EMG sig-
nals: C4 and S5
1
DWT and WPT moments should not be confused
with wavelet vanishing moments.
WAVELET TRANSFORM MOMENTS FOR FEATURE EXTRACTION FROM TEMPORAL SIGNALS
73

In order to reduce the dimensionality and to
smooth out the noise, we applied six moments to
transformed signals (DWT and WPT):
1
0
[ ], 0,1, 2,...,5,
j
m
N
m
n
j
n
MSnm
N
−
=
⎛⎞
==
⎜⎟
⎜⎟
⎝⎠
∑
(5)
where
represents sequences A, D, AA, DD, AD
and DA used in algorithms described below, while N
j
is number of samples at the corresponding level of
decomposition.
[]Sn
The new approach based on DWT consists of the
following steps:
1. Perform two-scale decomposition of the input
signal;
2. Compute moments for three transform se-
quences (D, AA, AD);
3. Apply logarithm transform to each feature,
log(0.1+f);
4. Normalize all features using mean value and
standard deviation computed for each feature
across all samples.
The choice of sequences D, AA and AD was
made empirically; it has given the best results in av-
erage for the given set of data. Similar choice was
made for WPT algorithm.
The WPT-based method has the following steps:
1. Perform two-scale decomposition of the input
signal;
2. Select basis obtained from previous application
of the best basis Coifman algorithm;
3. Compute moments for three transform se-
quences (A, DA, DD);
4. Apply logarithm transform to each feature,
log(0.1+f);
5. Normalize all features using mean value and
standard deviation computed for each feature
across all samples.
The optimal basis selection in this method was
based on a single channel. The same basis thus ob-
tained was subsequently used for single and multiple
channels, and for different sequence lengths.
Log transformation was applied to moments as it
effectively reduces the skewness and the kurtosis of
data, consequently resulting in an estimated probabil-
ity density that appears more like normal distribution
(Vuskovic atal. 1995). The nonlinear transformation
of features has significantly improved the classifier
performance.
7 THE SVM CLASSIFIER
The support vector machines ( Christianini & Shaw-
Taylor 2000) are a family of learning algorithms
based on the work of Vapnik (1998), which have
recently gained a considerable interest in pattern
recognition community. The success of SVM comes
from their good generalization ability, robustness in
high dimensional feature spaces and good computa-
tional efficiency.
In this work, a standard SVM classifier with lin-
ear kernel has been used for dichotomic (binary)
classification (Gunn 1997). The multiclass SVM can
also be considered, but this is out of the scope of this
paper.
The previous work on the classification of pre-
hensile EMG patterns (Vuskovic 1996) has shown
that the most difficult is to discriminate cylindrical
from spherical grasps (C/S), and then lateral from
precision grasps (L/P). Therefore the SVM is applied
to these pairs of grasp types and the feature extrac-
tion methods were evaluated accordingly.
The classification tests were performed with
leave-one-out method, where one sample was re-
moved from the data set and the rest of the samples
were used to train the SVM. The procedure was re-
peated for each sample in the data set, and the aver-
age hit rate was computed afterwards.
8 COMPUTATIONAL
COMPLEXITY
Application of WPT and calculation of J scales,
2
log
≤
J
N , where N is the length of the original
temporal signal, results in JN coefficients. Conse-
quently, the computational cost of the full-scale
WPT is in the order of
2
(Englehart 2001). Similarly, the computational com-
plexity of full-scale DWT is half the computational
complexity of the WPT, i.e.
()≤OJN (log )ON N
()
2
log 2ON N
. Since
our new approaches use only two-scale DWT or
two-scale WPT decomposition, we can enumerate
all the approaches with respect to their computa-
tional complexity in the increasing order: DWT(new)
< WPT (new) < DWT (Englehart) < WPT (Engle-
hart). The complexities are summarized in table 1.
Table 1: Computational complexity
New approach Englehart
DWT WPT DWT WPT
O(N) O(2N) O(N logN/2) O(N logN)
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
74

9 EXPERIMENTAL
EVALUATION
In this section we discuss the methodology for the
experimental evaluation of DWT and WPT ap-
proaches.
9.1 Cluster Visualization
In order to compare the effectiveness of a feature
extraction method there is needed some method to
compare the discrimination of clusters in feature
space, either by 2D or 3D scatter plots, or by some
distance measure between clusters. Both methods
are normally based on the transformation of the fea-
ture space through PCA or Fisher-Rao transform,
which both use the inverse of the cluster covariance
matrices. Unfortunately the dimensionality of the
feature space is often larger than the number of sam-
ples, which makes the methods inapplicable due to
the singularity or ill-conditioning of the covariance
matrices. However, the support vector machines of-
fered new possibilities. SVM maximize the margin
between clusters and the separation hyperplane in the
original or kernel-induced feature space without a
need to use covariance matrices.
We use in this work a projection of the original
feature space onto the line perpendicular to the
maximal-margin separation hyperplane:
(6) ,
T
pXw=
where X is N×d sample (feature) matrix, w is unit, d-
dimensional normal to the separation hyperplane,
and p is N-vector of projected samples. In order to
get a 2D plot of samples another projection vector is
needed:
(7) .
T
qXu=
The d-dimensional projection vector u doesn't
have to be orthonormal to w, but has to be unique in
some way. Therefore we used the direction of the
minimal variance of both clusters, which is nearly
laying in the separation hyperplane. The vector co-
incides with the eigenvector that corresponds to the
smallest non-zero eigenvalue of the pooled covari-
ance matrix:
112 2
12
12
(1)( 1)
(, ) ,
2
NSNS
S pool S S
NN
−+−
==
+−
(8)
where N
i
(N
1
+N
2
= N) and S
i
are sizes and covari-
ance matrices of the two clusters. An example of
cluster diagrams, plot(p,q), is shown in figure 3,
which will be discussed later.
9.2 Hotelling Distance
A useful quantitative measure of cluster discrimina-
tion in multidimensional space is Hotelling distance
between cluster means (T
2
statistic). The T
2
can be
computed for projected clusters:
21
12
12 12
12
12
()(
(, ),
T
NN
TccCc
NN
C pool C C
−
=−
+
=
),
c
−
(9),
where
i
c and C
i
are sample means and sample co-
variance matrices of projected clusters respectively.
In order to establish the significance of the distance
under some confidence level, the T
2
distance needs
to be compared with the corresponding critical value
. The critical value can be obtained if we assume
that the quantity
2
c
T
2
12
12
(1
(2
NNr
T
NN r
)
)
+
−−
+−
has F-distribution with degrees of freedom r and
12
1
f
NNr
=
+−−, where r = 2 in case of 2D pro-
jections (Seber 1984). The above is true under the
assumption that clusters have normal distributions
with nearly equal sizes and covariance matrices. If
this is not the case, a stronger statistic has to be used.
In this work we used statistic suggested in (Yao
1965), where the cluster distance was computed as:
()
1
2
12 11 2 2 12
()/ / (
T
TccCNCN cc
−
=− + −).
T
(10)
The degrees of freedom for the F-distribution
were estimated from the data (Seber 1984) (not pre-
sented here due to limited space). The test works for
unequal clusters that can have any bell-shaped dis-
tribution. The
T
2
values are shown in tables 2 and 3,
and in the scatter diagrams in figure 3. The critical
values
c
were all below 11. The value of cluster
distances as a quantitative measure of cluster dis-
crimination is that they can be easily and quickly
computed.
2
9.3 Number of Moments
Once the classification pairs are determined, the next
step is to determine the optimal number of DWT and
WPT moments, which will be used for feature
reduction. This was done experimentally by
extensive
application of feature extractions and classiffications
to different EMG signal lengths and different number
of channels.
WAVELET TRANSFORM MOMENTS FOR FEATURE EXTRACTION FROM TEMPORAL SIGNALS
75

Based on the bar graphs the selection of five mo-
ments (
M
0
, M
1
,…,M
4
) was a clear choice.
10 THE RESULTS
The comparison of four different approaches: the
five-moment DWT and WPT as proposed in this pa-
per, and the DWT and WPT of Englehart (1998a,
1999) have been measured by Hotteling distances and
by the classification hit rates applied to two cluster
pairs (C/S) and (L/P).
The results are presented in tables 2 through 5.
The feature extraction was performed for 200 and 400
ms time sequences recorded from a single channel
and from four simultaneous channels. Each channel
represented one surface EMG electrode attached to
the upper-forehand of the subject. Several different
wavelets were used in experiments, but only the two
most successful ones were shown here: the fourth-
order Coifman wavelets (C4) and the fifth-order sym-
lets (S5). The two tables show a roughly good corre-
lation between the Hotelling distances and the classi-
fication hit-rates. The small differences can be ex-
plained by the fact that the Hotelling distances point
the goodness of clustering, while the hit rates stress
the generalization of the trained SVM.
An example of four different cluster scatter dia-
grams is shown in figure 3.
Figure 2: Hotelling distances versus number of
m
oments
for WPT: (a) 200 ms, single channel, (b) 200ms, four
channels, (c) 400 ms, single channel, (d) 400 ms, four
channels (C/S grasps – lower bars, L/P grasps upper bar
Figure 3: SVM-projected clusters, 200 ms, and four chan-
nels, WPT: (a) C/S - new approach, (b) L/P - new
ap-
proach, (c) C/S - Englehart, (d) L/P - Englehart
The results suggest clear advantage of our novel
method over the Englehart’s approaches mainly due
to the moments used for dimensionality reduction,
instead of applying PCA. In addition, the application
of log transformation on features has helped consid-
erably. Our WPT novel method seems to behave
better at classifying the 200 ms sequences. This is
due to the WPT basis selection, which better charac-
terizes the frequency structure of the transient sig-
nals.
Table 2: Hotelling distances (C/S)
New approach Englehart
WT WPT
Sig.
length
/chnls
C4 S5 C4 S5
DWT
C4
WPT
S5
200/1 75 61 109 97 49 13
200/4
352 466 424 421 201 73
400/1 92 79 96 79 480 45
400/4 366 570 535 488 295 100
Table 3: Hotelling distances (L/P)
New approach Englehart
DWT WPT
Sig.
length
/chnls
C4 S5 C4 S5
DWT
C4
WPT
S5
200/1 33 65 44 100 362 11
200/4 289 3462 1724 723 756 107
400/1 178 166 233 262 118 60
400/4 560 24680 1472 718 2388 168
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
76
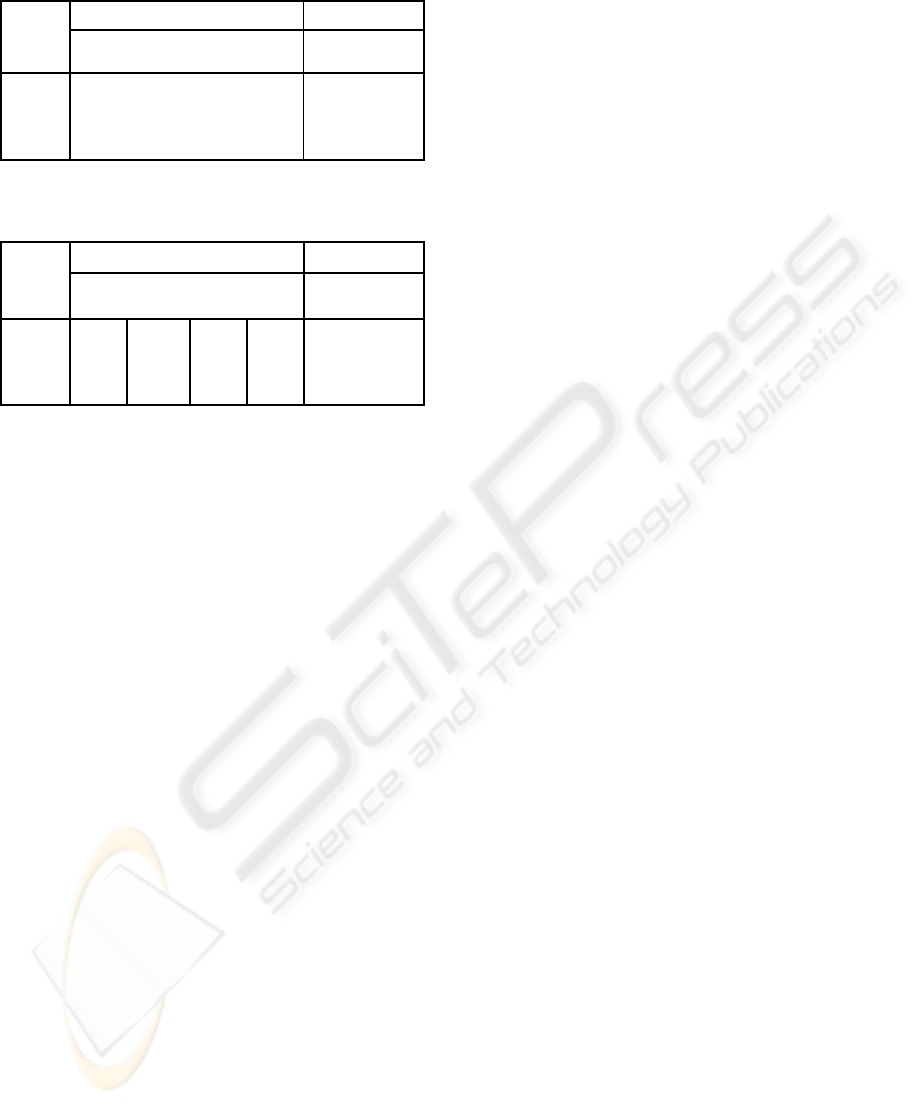
Table 4: Classification hit rates in % (C/S)
New approach Englehart
WT WPT
Sig.
length
/chnls
CO4 SY5 CO4 SY5
DWT
C4
WPT
S5
200/1 75.0 76.7 79.2 79.2 60.8 62.5
200/4 90.0 94.2 94.2 95.0 86.7 88.3
400/1 80.8 80.0 80.8 77.5 60.8 59.2
400/4 99.2 96. 7 98.3 97.5 88.3 93.3
Table 5: Classification hit rates in % (L/P)
New approach Englehart
WT WPT
Sig.
length
/chnls
CO4 SY5 CO4 SY5
WT WPT
200/1 73.3 81.7 81.7 83.3 56.7 53.3
200/4 91.7 96.7 90.0 98.3 80.0 93.3
400/1 96.7 95.0 93.3 91.7 56.7 63.3
400/4 99.9 99.9 99.9 99.9 88.3 95.0
11 CONCLUSIONS
A new approach of wavelet-based feature extraction
from temporal signals has been proposed. The ap-
proach extends the Englehart's discrete wavelet trans-
form and wavelet packet transform by subjecting the
two-scale, three-sequence wavelet coefficients to
temporal moment computation. This has helped re-
duce significantly the dimensionality of the resulting
feature vectors without loosing the essential informa-
tion in the original patterns. It was found experimen-
tally that first five raw moments represent a good
compromise. The new methods are applied to pre-
hensile EMG signals of various lengths and various
amounts of input signals (surface EMG channels)
and compared to the best approaches of Englehart, on
the same set of signals. For the comparison are used
two quantitative measures: Hotelling statistic and
classification hit rates. The classifier applied to the
extracted features was linear support vector machine,
which has exceptionally good performance in case of
large feature spaces and fewer training samples. The
results have shown superior performance of the new
approach. A brief complexity analysis also shows
that the new approach is more efficient time wise.
Although the methodology was demonstrated on
EMG signals, we believe the methodology can
equally successfully be applied to other temporal
signals.
REFERENCES
Christianini N., Shawe-Taylor, 2000. An Introduction to
Support Vector Machines. Cambridge Univ. Press.
Du S. and Vuskovic M., 2004. Temporal vs. Spectral
approach to Feature Extraction from Prehensile EMG
Signals. In IEEE Int. Conf. on Information Reuse and
Integration (IEEE IRI-2004), Las Vegas, Nevada.
Englehart K., Hudgins B., Parker P. and Stevenson M.,
1998. Time-frequency representation for classification
of the transient myoelectric signal. In ICEMBS’98.
Proceedings of the 20th Annual International Confer-
ence on Engineering in Medicine and Biology Society.
ICEMBS Press.
Englehart K., 1998a. Signal Representation for Classifica-
tion of the Transient Myoelectric Signal. Doctoral
Thesis. University of New Brunswick, Fredericton,
New Brunswick, Canada.
Englehart K., Hudgins B., Parker P. and Stevenson M.,
1999. Improving Myoelectric Signal Classification us-
ing Wavelet Packets and Principle Component Analy-
sis. In ICEMBS’99. Proceedings of the 21st Annual In-
ternational Conference on Engineering in Medicine
and Biology Society, ICEMBS Press.
Englehart K., Hudgins B., Parker P., 2001. A Wavelet –
Based Continuous Classification Scheme for Multi-
fucntion Myoelectric Control. In IEEE Transactions
on Biomedical Engineering, vol. 48, No. 3, pp. 302-
311.
Farry, K. A., Walker I. D., Baraniuk R. G., 1996.
Myoelectric Teleoperation of a Complex Robotic
Hand. IEEE Trans On Robotic and Automation, Vol.
12, No.5.
Gunn S.R., 1997. Support Vector Machines for Classifica-
tion and Regression. Technical Report, Image Speech
and Intelligent Systems Research Group, University of
Southampton.
Hannaford B. and Lehman S., 1986. Short Time Fourier
Analysis of the Electromyogram: Fast Movements and
Constant Contraction. In IEEE Transactions On Bio-
medical Engineering. BME-33,
Han-Pan Huang H-P, Chen C_Y., 1999. Development of a
Myoelectric Discrimination System for Multi-Degree
Prosthetic Hand. Proc. of the 1999 International Con-
ference on Robotics and Automation, Detroit, May pp.
2392-2397.
Hudgins, P. Parker and R.N. Scott, 1991. A Neural Net-
work Classifier for Multifunctional Myoelectric Con-
trol. Annual Int. Conf. Of the EMBS, Vol. 13, No. 3,
pp. 1454-1455.
Hudgins B., Parker P. and Scott R. N., 1993. A New Strat-
egy for Multifunctional Myoelectric Control. In IEEE
Transactions on Biomedical Engineering, vol. 40, No.
1, pp. 82-94.
Saito N. and Coifman R. R., 1995. Local Discriminant
Basis and their applications. J. Math. Imag. Vis., Vol.
5, no 4, pp. 337-358.
Nishikawa D, Yu W. Yokoi H, and Kakazu Y, 1991. EMG
Prosthetic Hand Controller using Real-Time Learning
WAVELET TRANSFORM MOMENTS FOR FEATURE EXTRACTION FROM TEMPORAL SIGNALS
77

Method. In Proc. of the IEEE Conf. on SMC, Vol. 1,
pp. I 153-158.
Carreño I. R., Vuskovic M., 2005. Wavelet-Based Feature
Extraction from Prehensile EMG Signals. In 13th
NordicBaltic on Biomedical Engineering and Medical
Physics (NBC'05 UMEA), Umea, Sweden, 13-17.
Schlesinger, D., 1919. Der Mechanische Aufbau der
Kunstlishen Glieder. In Ersatzglieder und Arbeitshil-
fen, Springer, Berlin.
Seber G.A.F., 1984. Multivariate Observations, John
Wiley & Sons, pp 102-117.
Uchida N. U., Hiraiwa A., Sonehara N., Shimohara K.,
1992. EMG Pattern Recognition by Neural Networks
for Multi Fingers Control. Proc. of the Annual Int.
Conf. of the Engineering in Medicine and Biology So-
ciety. Vol 14, Paris, pp.1016-1018.
Vapnik V. N., 1998. Statistical Learning Theory. John
Wiley & Sons.
Vuskovic M., Pozos A. L., Pozos R, 1995. Classification
of Grasp Modes Based on Electromyographic Patterns
of Preshaping Motions. Proc. of the Internat. Confer-
ence on Systems, Man and Cybernetics. Vancouver,
B.C., Canada, pp. 89-95, 1995.
Vuskovic M., Schmit J., Dundon B. Konopka C., 1996.
Hierachical Discrimination of Grasp Modes Using
Surface EMGs. Proc. of the Internat. IEEE Confer-
ence on Robotics and Automation, Minneapolis, Min-
nesota, April 22-28. 2477-2483.
Yao, Y., 1965. An Approximate Degrees of Freedom So-
lution to the Multivariate Behrens-Fisher Problem,
Biometrica, Vol. 52, 139-147.
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
78
