STABILITY ANALYSIS OF A THREE-TIME SCALE SINGULAR
PERTURBATION CONTROL FOR A RADIO-CONTROL
HELICOPTER ON A PLATFORM
Sergio Esteban, Francisco Gordillo and Javier Aracil
Departamento de Ingenier
´
ıa de Sistemas y Autom
´
atica
Camino de los descubrimientos s/n, Sevilla, 41092, Spain
Keywords:
Helicopter control, nonlinear systems, singular perturbation.
Abstract:
A stability analysis is conducted on the proposed three-time scale singular perturbation control that is applied
to a Radio/Control helicopter on a platform to regulate its vertical position. The control law proposed allows
to achieve the desired altitude by either selecting a desired collective pitch angle or a desired angular velocity
of the blades.
1 INTRODUCTION
Control of rotatory wing aircrafts represents a very
challenging task due to the nonlinearities and inherit
instabilities present in such systems. The versatility
of rotorcrafts allows them to perform almost any task
that no conventional aircraft can do, but this ability
is ultimately associated to the degree of stability and
control characteristics obtained via automatic control
design (Curtis, 2003). These stability and control
characteristics come at the expense of the complex
control designs that are required to deal with these
highly nonlinear aerospace systems. The increased
performance requirements of a continuously growing
aerospace industry has called for better control de-
signs that can deal with the more complex systems,
making linear control techniques insufficient to cope
with the industry demands.
During the last decades, a wide range of different
nonlinear control techniques have been studied to deal
with the nonlinear dynamics of aerospace systems.
Some of these techniques include singular perturba-
tion (Kokotovi
´
c et al., 1986), feedback linearization
(Meyer et al., 1984), dynamic inversion (Bugajski
et al., 1990; Reiner et al., 1995; Snell et al., 1992),
sliding mode control(Sira-Ramirez et al., 1994), or
backstepping control methods (Khalil, 1996; Lee
and Kim, 2001) to name few. Neural Networks
(NN) are also included within the realm of non-
linear control techniques, and extensive work has
also been conducted including Adaptive Critic Neural
Network (ACNN) based controls (Balakrishnan and
Huang, 2001), feedback linearization along with
neural-networks as an alternative to gain scheduling
(Leiter et al., 1995; Calise et al., 1999), Neural Gener-
alized Predictive Control (NGPC) algorithms capable
of real-time control law reconfiguration (Haley and
Soloway, 2001), or generic neural flight control and
autopilot systems (Bull et al., 2000) to name few.
A basic problem in control design is the mathe-
matical modelling complexity and precision required
for the control designs to have a good performance.
The modelling of many systems calls for high-order
dynamic equations, which for the case of rotorcraft
systems represents a unique challenge: in addition
to the modelling complexity of aerodynamic surfaces
for a wide range of conditions, it is necessary to
take into account the added complexity of the rota-
tory machinery associated to the aerodynamic sur-
faces. Generally, the presence of parasitic parame-
ters such as small time constants is often the source
of a increased order and stiffness of these systems
(Naidu and Calise, 2001). The stiffness, attributed
to the simultaneous occurrence of slow and fast phe-
nomena, gives rise to time-scales, and the suppres-
sion of the small parasitic variables results in dege-
nerated, reduced order systems, called singularly per-
turbed systems, that can be stabilized separately, and
thus simplifying the burden of control design of high-
order systems. The literature gives a extended survey
of the use of singular perturbed and time-scales con-
trol methods in aerospace systems (Naidu and Calise,
2001; Naidu, 2002).
The motivation to this article comes from the work
49
Esteban S., Gordillo F. and Aracil J. (2005).
STABILITY ANALYSIS OF A THREE-TIME SCALE SINGULAR PERTURBATION CONTROL FOR A RADIO-CONTROL HELICOPTER ON A
PLATFORM.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 49-58
DOI: 10.5220/0001190500490058
Copyright
c
 SciTePress

of (Sira-Ramirez et al., 1994) that used a dynamical
multivariable discontinuous feedback control strategy
of the sliding mode type for the stabilization of a
nonlinear helicopter model in vertical flight which
include the dynamics of the collective pitch actua-
tors. This article analyzes extensively, for the range
of desired final values, the stability of the closed loop
system for the singular perturbation control law pro-
posed by the authors (Esteban et al., 2005), which was
shown to outperform the results presented by (Sira-
Ramirez et al., 1994). This article is structured as fol-
lows: Section 2 presents the helicopter model used
throughout this article, including an analysis of the
equilibrium points of the model; Section 3 introduces
the singular perturbation control law formulation de-
rived in (Esteban et al., 2005); the stability analysis
of the closed loop system is developed in section 4;
simulation results of the closed loop system are de-
picted in Section 5, conclusions and future work are
described in Section 6 and figures of the computer
simulations are shown in Section 6.
2 MODEL DEFINITION
The helicopter model that will used throughout the re-
mainder of this article is obtained from several techni-
cal reports that were written at the University of Pur-
due (Pallet et al., 1991; Pallet and Ahmad, 1991) that
describe the vertical motion of a radio/control heli-
copter model mounted on a stand as seen in Fig. 1.
The model includes the nonlinear vertical motion of
the helicopter and the nonlinear dynamics of the col-
lective pitch actuators, which increases considerably
the complexity of the model but also depicts a more
realistic model. The differential set of equations
that describes the vertical motion of the X-Cell 50
(Miniature-Aircraft-USA, 1999) model miniature he-
licopter are
¨z = K
1
(1 + G
eff
)C
T
ω
2
−g −K
2
˙z −K
3
˙z
2
−K
4
, (1)
where C
T
is the thrust coefficient of the helicopter
model, ω (radians) is the rotational speed of the
rotor blades, z (meters) is the height of the he-
licopter above the ground, g (m/s
2
) is the gravi-
tational acceleration, and G
eff
models the ground
effect, but during the remainder of this article it will
be considered negligible (G
eff
= 0). The thrust co-
efficient and the dynamics of the angular velocity of
the blades are modelled as
C
T
=
−K
C1
+ K
2
C1
+ K
C2
θ
c
2
(2)
˙ω = −K
5
ω − K
6
ω
2
− K
7
ω
2
sin θ
c
+ K
8
u
th
+ K
9
, (3)
where θ
c
(rad) is the collective pitch angle of the ro-
tor blades. The dynamics of the collective pitch angle
are defined as
¨
θ
c
= K
10
(−0.00031746u
θ
c
+ 0.5436 − θ
c
) −
K
11
˙
θ
c
− K
12
ω
2
sin θ
c
, (4)
where the inputs to the system are the throttle(u
th
)
and the input to the collective servomechanism (u
θ
c
).
The nominal values of the parameters are K
1
=0.25,
K
2
=0.1, K
3
=0.1, K
4
=7.86, K
5
=0.7, K
6
=0.0028,
K
7
=0.005, K
8
=-0.1088, K
9
=-13.92, K
10
=800,
K
11
=65, K
12
=0.1, K
C
1
=0.03259, K
C
1
=0.061456,
and g=9.81. Equations (1), (3) and (4) can be written
into the non linear equations of motion by defining
the state space vector as
x =
z
˙z
ω
θ
c
˙
θ
c
=
x
1
x
2
x
3
x
4
x
5
. (5)
being the resulting nonlinear equations of motion,
˙x
1
= x
2
˙x
2
= x
2
3
(a
1
+ a
2
x
4
−
√
a
3
+ a
4
x
4
) + a
5
x
2
+ a
6
x
2
2
+ a
7
˙x
3
= a
8
x
3
+ a
10
x
2
3
sin x
4
+ a
9
x
2
3
+ a
11
+ u
1
(6)
˙x
4
= x
5
˙x
5
= a
13
x
4
+ a
14
x
2
3
sin x
4
+ a
15
x
5
+ a
12
+ u
2
,
where the constants are a
1
=5.31×10
−4
, a
2
=1.5364×
10
−2
, a
3
=2.82 × 10
−7
, a
4
=1.632 × 10
−5
, a
5
=-
K
2
, a
6
=-K
2
, a
7
=-g-K
4
, a
8
=-K
5
, a
9
=-K
6
, a
10
=-K
6
,
a
11
=K
9
, a
12
=0.5436K
10
, a
13
=-K
10
, a
14
=-K
12
, and
a
15
=-K
11
.
2.1 Equilibrium Points Analysis of
the Helicopter Model
In order to better understand the behavior of the sys-
tem, an analysis of the equilibrium points is con-
ducted. The equilibrium points are obtained by
setting all the derivatives of system (6) to zero thus
yielding the equilibrium equations
0 = x
2
0 = x
2
3
(a
1
+ a
2
x
4
−
√
a
3
+ a
4
x
4
) + a
5
x
2
+
a
6
x
2
2
+ a
7
0 = a
8
x
3
+ a
10
x
2
3
sin x
4
+ a
9
x
2
3
+ a
11
+ u
1
(7)
0 = x
5
0 = a
13
x
4
+ a
14
x
2
3
sin x
4
+ a
15
x
5
+ a
12
+ u
2
.
As seen in the previous section, the system is
formed by five state variables, and two control sig-
nals, therefore two degrees of freedom are expected,
but when conducted the equilibrium points analysis,
only one degree of freedom is observed, three equa-
tions with four unknowns (¯x
3
, ¯x
4
, ¯u
1
, ¯u
2
), where the
bar denotes the value at equilibrium,
0 = ¯x
2
3
(a
1
+ a
2
¯x
4
−
√
a
3
+ a
4
¯x
4
) + a
7
(8)
0 = a
8
¯x
3
+ a
10
¯x
2
3
sin ¯x
4
+ a
9
¯x
2
3
+ a
11
+ ¯u
1
(9)
0 = a
13
¯x
4
+ a
14
¯x
2
3
sin ¯x
4
+ a
12
+ ¯u
2
, (10)
and the vertical velocity of the helicopter and the
collective pitch rate of the blades is equal to zero
ICINCO 2005 - ROBOTICS AND AUTOMATION
50

(¯x
2
= ¯x
5
= 0). This is caused because the heli-
copter equilibrium altitude (¯x
1
) does not show in any
of the equilibrium equations, therefore every equilib-
rium point can be attained at any altitude. This im-
plies that there exists an infinitely number of equilib-
rium points, and one of the variables needs to be fixed
in order to determine a single equilibrium point. The
first equilibrium equation, Eq. (8), defines the equilib-
rium space by selecting a desired value for either ¯x
3
or ¯x
4
, such that an expression can be determined as a
function of the selected desired variable, defined from
now on as x
3
D
or x
4
D
respectively. The last Eqs. (9-
10), define the control signals required for achieving
the selected equilibrium points. If the collective pitch
angle (x
4
D
) is selected as the fixed variable, the ex-
pressions to determine the values of the other three
unknowns as a function of de fixed variable (¯x
3
(x
4
D
),
¯u
1
(x
4
D
) and ¯u
2
(x
4
D
)) can be expressed as,
¯x
3
= ±
−
a
7
a
1
+ a
2
x
4
D
−
√
a
3
+ x
4
D
a
4
(11)
¯u
1
= −a
8
−
a
7
a
1
+ a
2
x
4
D
−
√
a
3
+ a
4
x
4
D
+
a
7
(a
10
sin x
4
D
+ a
9
)
a
1
+ a
2
x
4
D
−
√
a
3
+ a
4
x
4
D
− a
11
(12)
¯u
2
= −a
12
+
a
7
a
14
sin x
4
D
a
1
+ a
2
x
4
D
−
√
a
3
+ a
4
x
4
D
−
a
13
x
4
D
. (13)
If the angular velocity of the blades (x
3
D
) is se-
lected as the fixed variable, the expressions to de-
termine the values of the other three unknowns as a
function of de fixed variable (¯x
4
(x
3
D
), ¯u
1
(x
3
D
) and
¯u
2
(x
3
D
)) can be expressed as
¯x
4
=
a
4
x
3
D
±
K
b
x
2
3
D
+ K
c
2a
2
2
x
3
D
+ K
d
+
K
e
x
2
3
D
, (14)
¯u
1
= −a
8
x
3
D
− x
2
3
D
(a
10
sin ¯x
4
+ a
9
) − a
11
(15)
¯u
2
= −a
13
¯x
4
− a
14
x
2
3
D
sin ¯x
4
− a
12
, (16)
being the coefficients defined by
K
b
= a
2
4
− 4a
2
a
1
a
4
+ 4a
2
2
a
3
K
c
= −4a
2
a
7
a
4
K
d
= −
a
1
a
2
K
e
= −
a
7
a
2
.
It can be observed that Eq. (11) has two solu-
tions for the equilibrium rotational speed of the blades
(¯x
3
), but constrained by the physical rotation of the
blades, only the positive solution is considered. It
is also observed that Eq. (14) has two solutions for
the equilibrium collective pitch angle of the blades
(¯x
4
), but it can be checked by substituting both so-
lutions in the original equations (7) that the solution
corresponding to the minus sign in front of the square
root is a false solution introduced in the previous
computations, therefore only the positive solution is
considered. Note that in both Eq. (15) and Eq. (15)
depend on ¯x
4
defined in Eq. (14).
3 SINGULAR PERTURBATION
FORMULATION
The general two-time scale singular perturbation
model formulation is described (Kokotovi
´
c et al.,
1986) as,
˙x = f(x, z, ε, t), x(t
0
) = x
0
, x ∈ R
n
(17)
ε ˙z = g(x, z, ε, t), z(t
0
) = z
0
, z ∈ R
m
, (18)
and its quasi-steady-state condition is obtained when
ε = 0 thus reducing the dimension of the state space
defined in Eqs. (17) and (18) from n + m to n. This
quasy-steady state condition of the differential equa-
tion that represents the ε-fast dynamics degenerates
into the algebraic equation
0 = g(¯x, ¯z, 0, t), (19)
where the bar denotes that the variables belong to a
system with ε = 0. The new model is considered in
standard form if and only if in a domain of interest,
Eq. (19), has k ≥ 1 distinct real roots (Kokotovi
´
c
et al., 1986):
¯z =
¯
φ
i
(¯x, t), i = 1, 2, ..., k. (20)
This assumption assures that a well defined n-
dimensional reduced model will correspond to each
root of Eq. (20). To obtain the i
th
reduced model, Eq.
(20) is substituted into Eq. (17) yielding
˙
¯x = f(¯x, ¯z,
¯
φ
i
(¯x, t), 0, t), ¯x(t
0
) = x
0
, (21)
and keep the same initial conditions for the state
variable ¯x(t) as for x(t). Using singular perturba-
tion techniques causes the dynamics to behave as a
multi-time-scale system simplifying considerably the
complexity of the dynamics. The slow response is ap-
proximated by the reduced model (21), while the dis-
crepancy between the response of the reduced model,
(21), and that of the full model (17) and (18), is the
fast transient.
3.1 Multi-time Scale Singular
Perturbation Model Formulation
(Esteban et al., 2005) showed that a three-time scale
helicopter model was intuitively more precise than a
two-time scale due to the treatment of the collective
pitch angle as a state variable, generally being treated
as a control input. The general formulation of the
three-time scale singular perturbed systems requieres
STABILITY ANALYSIS OF A THREE-TIME SCALE SINGULAR PERTURBATION CONTROL FOR A
RADIO-CONTROL HELICOPTER ON A PLATFORM
51

the system to posses three different time-scales that
are defined as
ζ ˙x = f (x, y, z, ε, t )
˙y = g(x, y, z, ε, t) (22)
˙z = εh(x, y, z, ε, t),
being 0 < ζ << 1 and 0 < ε << 1. For the heli-
copter model, the fast dynamics are defined as
ζ ˙x
4
= ζx
5
ζ ˙x
5
= −x
4
+ c
1
x
2
3
sin x
4
+ c
2
x
5
+ c
3
+
c
4
u
2
(23)
while the intermediate-dynamics are
˙x
1
= x
2
˙x
2
= x
2
3
(a
1
+ a
2
x
4
−
√
a
3
+ a
4
x
4
) + a
5
x
2
+
a
6
x
2
2
+ a
7
, (24)
and the slow-dynamics are
˙x
3
= ε
c
5
x
3
− x
2
3
sin x
4
− x
2
3
+ c
6
+ c
7
u
1
. (25)
The the parasitic constants are chosen to be ζ =
−
1
a
13
= 0.00125 and ε =
−1
a
10
= 0.0028, and the
constants of the parameters are
c
1
= −
a
14
a
13
= ζa
14
, c
2
= −
a
15
a
13
= ζa
15
c
3
= −
a
12
a
13
= ζa
12
, c
4
= −
1
a
13
= ζ
c
5
= −
a
8
a
10
= εa
8
, c
6
= −
a
11
a
10
= εa
11
c
7
= −
1
a
10
= ε.
The control strategy for the three-time scale sin-
gular perturbation formulation consists in treating
the three different scales as two distinct singular
perturbed problems. The first problem considers
the fast and intermediate dynamics, and obtains the
associated control law that stabilizes the first sub-
system using singular perturbation methodology de-
scribed in the previous section. For this subsystem,
the collective pitch angle dynamics (x
4
, x
5
) are the
ζ-fast dynamics and the vertical motion of the heli-
copter (x
1
, x
2
) are the ζ-slow dynamics. The second
problem considers the intermediate and slow dynam-
ics, being the vertical motion of the helicopter the ε-
fast dynamics and the angular velocity of the blades
(x
3
) the ε-slow dynamics of the system.
3.1.1 Control formulation for the ζ-singular
perturbation subsystem
Prior to determine the control law for the ζ-singular
perturbation subsystem, a change of variables is re-
quired in the ζ-fast dynamics, Eq. (23), to allow
solving for the root of the manifold 0 = f(¯x, ¯y, 0, t).
A feedback transform is introduced such that
¯u
2
= c
1
x
2
3
sin x
4
+ c
4
u
2
,
thus rewriting Eq. (23) into
ζ ˙x
4
= ζx
5
(26)
ζ ˙x
5
= −x
4
+ c
2
x
5
+ c
3
+ ¯u
2
. (27)
Setting ζ = 0 yields the root for the fast-dynamics,
¯x
5
= 0 (28)
¯x
4
= ¯u
2
+ c
3
. (29)
Substituting for ¯x
4
and ¯x
5
into the intermediate dy-
namics generates the reduced degenerated system,
˙x
1
= x
2
˙x
2
= x
2
3
(a
1
+ a
2
(¯u
2
+ c
3
) −
a
3
+ a
4
(¯u
2
+ c
3
)) +
a
5
x
2
+ a
6
x
2
2
+ a
7
, (30)
In order to obtain the control law that stabilizes the
ζ-subsystem, a series of algebraic substitutions are
conducted. Let
w
2
= a
3
+ a
4
(¯u
2
+ c
3
). (31)
and a expression of ¯u
2
as a function of w can be ob-
tained such as
¯u
2
=
w
2
− a
3
− a
4
c
3
a
4
, (32)
and substituting Eq. (31) and (32) into (33) yields
˙x
1
= x
2
˙x
2
= x
2
3
a
1
+ a
2
w
2
− a
3
− a
4
c
3
a
4
+ c
3
− w +
a
5
x
2
+ a
6
x
2
2
+ a
7
, (33)
which can be simplified into
˙x
1
= x
2
˙x
2
= x
2
3
c
8
w
2
− w + Ka + a
5
x
2
+
a
6
x
2
2
+ a
7
, (34)
being
c
8
=
a
2
a
4
, K
a
= a
1
+ a
2
c
3
−
a
2
(a
3
+ a
4
c
3
)
a
4
.
Let v = c
8
w
2
− w + K
a
, thus Eq. (34) becomes
˙x
1
= x
2
˙x
2
= x
2
3
v + a
5
x
2
+ a
6
x
2
2
+ a
7
. (35)
We choose a stable target system of the form
˙x
1
= x
2
˙x
2
= −b
1
(x
1
− x
1
D
) − b
2
x
2
, (36)
where b
1
, and b
2
are control design parameters that
determine the desired time response, and x
1
D
repre-
sents the desired altitude of the helicopter. The con-
trol problem can be solved if a v is chosen such that
system (35) behaves like the target system defined in
(36). The control signal v is therefore chosen to be:
v =
−a
6
x
2
2
− a
7
− dx
2
− b
1
(x
1
− x
1
D
)
x
2
3
, (37)
ICINCO 2005 - ROBOTICS AND AUTOMATION
52

where
d = b
2
+ a
5
. (38)
The control law u
2
can the obtained tracing back
the algebraic substitutions from the final target system
to the initial degenerated system such that
u
2
=
¯u
2
− c
1
x
2
3
sin x
4
c
4
, (39)
where ¯u
2
is
¯u
2
=
w
2
− a
3
− a
4
c
4
a
4
, (40)
where w can be obtained solving the quadratic poly-
nomial
c
8
w
2
− w + K
a
= v
c
8
w
2
− w + K
a
− v = 0, (41)
where v is defined by Eq. (37). Solving for the roots
of the polynomial in Eq. (41) yields
w =
1 ±
1 − 4c
8
(K
a
− v)
2c
8
. (42)
It can be checked by substituting in the original
equations (7) that the solution corresponding to the
minus sign in front of the square root is a false solu-
tion introduced in the previous computations. In the
following, only the positive root will be considered.
The control law for the u
2
(x
1
, x
1
D
, x
2
, x
3
, x
4
) is
therefore defined by
u
2
= K
f
1 + 1 − 4c
8
(K
a
− v)
2
+
K
g
+ K
h
x
2
3
sin x
4
, (43)
where
K
a
= a
1
+ a
2
c
3
−
a
2
(a
3
+ a
4
c
3
)
a
4
K
f
=
1
4a
4
c
4
c
2
8
K
g
= −
a
3
+ a
4
c
3
a
4
c
4
K
h
= −
c
1
c
4
.
Results will be discussed in Section 5
3.1.2 Control formulation for the ε singular
perturbation subsystem
Once the first control law for the fast-intermediate
system is obtained, the second control law to stabi-
lize the intermediate-slow system needs to be deter-
mined. The stabilized vertical motion dynamics be-
comes the ε-fast system, and the angular velocity of
the blades is the ε-slow system. Setting the manifold
0 = g(¯x, ¯y, 0, t). The root of the ε-fast manifold are
determined by setting 0 = g(¯x, ¯y, ¯z, 0, t), yielding
0 = x
2
0 = x
2
3
(a
1
+ a
2
x
4
−
√
a
3
+ a
4
x
4
) + a
5
x
2
+
a
6
x
2
2
+ a
7
which represents the first two of the equilibrium Eqs.
(7). The first equation yields that the vertical velocity
of the helicopter is zero for the ε-fast manifold, and
the second equation yields an expression that defines
the space of configuration for the vertical motion as a
function of both x
3
and x
4
.
x
2
3
(a
1
+ a
2
x
4
−
√
a
3
+ a
4
x
4
) + a
7
= 0, (44)
Solving Eq. (44) for both x
3
and x
4
, and
substituting the associated independent variable by
x
3
D
and x
4
D
respectively yields
φ
1
= ±
−
a
7
a
1
+ a
2
x
4
D
−
√
a
3
+ x
4
D
a
4
(45)
φ
2
=
a
4
x
3
D
±
K
b
x
2
3
D
+ K
c
2a
2
2
x
3
D
+ K
d
+
K
e
x
2
3
D
, (46)
where φ
1
(x
4
D
) represents the solution of the rotor
blade angular velocity in the ε-fast manifold when a
desired collective pitch angle (x
4
D
) is selected, and
φ
2
(x
3
D
) represents the solution of the collective pitch
angle in the ε-fast manifold when a desired rotor blade
angular velocity (x
3
D
) is selected. These two expres-
sion allow the designer to choose which one of the
variables is considered as the second desired state,
which is required to define the equilibrium points of
the helicopter. Note that both Eqs. (45) and (46) have
two distinct solutions depicted by the ± sign. As it
was shown in Section 2.1, it can be observed that Eq.
(45) has two solutions for the rotor blade angular ve-
locity in the ε-fast manifold, φ
1
, but constrained by
the physical rotation of the blades, only the positive
solution is considered. It is also observed that Eq.
(46) has two solutions for the collective pitch angle
in the ε-fast manifold, (φ
2
), but it can be checked by
substituting both solutions in the original equations
(7) that the solution corresponding to the minus sign
in front of the square root is a false solution intro-
duced in the previous computations, therefore in the
future only the positive solution will be considered.
Once the roots of the manifold 0 = g(¯x, ¯y, ¯z, 0, t)
are defined, the control laws can be obtained by sub-
stituting Eqs. (45) or (46) into the ε-slow dynamics
depending if the control law has to be solved for a
desired collective pitch angle, (x
4
D
), or a desired an-
gular velocity, (x
3
D
), respectively yielding:
˙x
3
= ε
c
5
φ
1
− φ
2
1
sin x
4
− φ
2
1
+ c
6
+ c
7
u
1
, (47)
or
˙x
3
= ε c
5
x
3
− x
2
3
sin φ
2
− x
2
3
+ c
6
+ c
7
u
1
. (48)
The control laws are obtained by defining a target
system of the form
˙x
3
= −εb
3
(x
3
− x
3
D
), (49)
where b
3
represents the desired dynamics of the angu-
lar velocity of the blades. The control law associated
STABILITY ANALYSIS OF A THREE-TIME SCALE SINGULAR PERTURBATION CONTROL FOR A
RADIO-CONTROL HELICOPTER ON A PLATFORM
53

to Eq. (47) for a desired collective pitch angle (x
4
D
)
is
u
1
(x
4
D
) = −
c
5
φ
1
− φ
2
1
sin x
4
D
− φ
2
1
+ c
6
c
7
−b
3
(x
3
− φ
1
), (50)
and the control law associated to Eq. (49) for a desired
angular velocity of the blades (x
3
D
) is
u
1
(x
3
D
) = −
c
5
x
3
D
− x
2
3
D
sin φ
2
− x
2
3
D
+ c
6
c
7
−
b
3
(x
3
− x
3
D
). (51)
Prior to analyze the effectiveness of the pro-
posed control laws for different final conditions, it is
necessary to define the limits of the set of desired fi-
nal conditions that will be considered (x
3
D
and x
4
D
).
For the limits of the angular velocity of the blades,
we assumed that the engine can physically generate a
maximum angular velocity of x
3
max
= 180 rads/sec.
For the range of collective pitch angles a maximum
collective pitch angle of x
4
max
= 0.25 rads. is
considered, and the minimum collective pitch angle
can be determined analyzing the modelization of the
thrust coefficient, Eq. (2), where it can be observed
that only collective pitch angles x
4
> −
K
2
C
1
K
C
1
= −
a
3
a
4
will be defined. Analysis of φ
1
shows that there is a
region within the collective pitch angle defined range,
that it is not defined as an attainable desire final con-
dition. This defines two distinctive regions of interest
for the collective pitch angle
x
4
lim
1
> x
4
D
> −
a
3
a
4
x
4
max
> x
4
D
> x
4
lim
2
being x
4
lim
1
and x
4
lim
2
the roots of the denominator
of φ
1
equal to zero,
x
4
lim
1
=
a
4
− 2a
1
a
2
−
a
2
4
− 4a
4
a
1
a
2
+ 4a
2
2
a
3
2a
2
2
x
4
lim
2
=
a
4
− 2a
1
a
2
+
a
2
4
− 4a
4
a
1
a
2
+ 4a
2
2
a
3
2a
2
2
,
substituting the constants, the ranges are defined as
−0.3992 × 10
−3
> x
4
D
> −0.1727 × 10
−1
0.25 > x
4
D
> 0.4138 × 10
−3
Figure 2 represent the relation of φ
1
(x
4
D
) and
φ
2
(x
3
D
) for the ranges of considered desired collec-
tive pitch angle and angular velocity of the blades.
Analyzing the results of Fig 2 in detail, it can be
seen that despite that entire range of desired final con-
ditions above used is defined, it is illogical to con-
sider desired collective pitch angle values x
4
D
<
4.8727
◦
since it requires angular velocities above 180
rads/sec to define this equilibrium conditions, thus the
range of desired collective pitch angle is reduced to
14.3239
◦
> x
4
D
> 4.8727
◦
. Results of the proposed
control law will be discussed in Section 5
4 STABILITY ANALYSIS OF THE
CLOSED LOOP
FORMULATION
In this section, the local asymptotic stability of the de-
sired equilibrium points is analyzed for the resultant
closed loop system. The indirect method of Lyapunov
is used: if all the eigenvalues of the Jacobian, evalu-
ated at the equilibrium, are in the open left-hand com-
plex plane, the equilibrium is asymptotically stable.
In the following, this condition is checked using the
Routh-Hurwitz stability criterion (Routh, 1905). A
necessary but not sufficient condition for every so-
lution of D(s) = 0 in the left-hand complex plane
says that all coefficients of the characteristic polyno-
mial must be greater than zero, otherwise the system
is unstable. The sufficient condition of the Routh-
Hurwitz criterion says that the number of roots of the
polynomial that are in the right half-plane is equal
to the number of sign changes in the first column of
the Routh table. Therefore all coefficients of the first
column must be positive. In order to construct the
Routh table, the characteristic polynomial of the sys-
tem to be tested is assumed to be of the form
D(s) = a
0
s
k
+ a
1
s
k−1
+ ··· + a
k−1
s + a
k
, (52)
The Routh table corresponding to the D(s) is ob-
tained by constructing the first two rows transcribing
the coefficients of D(s) in alternate rows as shown in
table 1. Each succeeding row of the table is completed
using entries in the two preceding rows, until there are
no more terms to be computed. In the left margin are
found a column of exactly k numbers α
1
, α
2
, . . ., α
k
for a kth-order system, where Routh-Hurwitz coeffi-
cients are
b
1
= a
2
− α
1
a
3
, b
2
= a
4
− α
1
a
5
c
1
= a
3
− α
2
b
2
, c
2
= a
5
(53)
d
1
= b
2
− α
3
c
2
, e
1
= c
2
= a
5
,
being the α
′
s defined by
α
1
=
1
a
1
, α
2
=
a
1
b
1
α
3
=
b
1
c
1
, α
4
=
c
1
d
1
(54)
α
5
=
d
1
e
1
Table 1: Routh table.
1 a
2
a
4
a
6
· · ·
a
1
a
3
a
5
a
7
· · ·
α
1
=
1
a
1
b
1
= a
2
− α
1
a
3
b
2
b
3
· · ·
α
2
=
a
1
b
1
c
1
= a
3
− α
2
b
2
c
2
· · ·
α
3
=
b
1
c
1
d
1
= b
2
− α
3
c
2
· · ·
α
4
=
c
1
d
1
· · ·
.
.
.
ICINCO 2005 - ROBOTICS AND AUTOMATION
54

The Routh-Hurwitz criterion states that the roots of
D(s) = 0 lie in the left half-plane, excluding the
imaginary axis, if and only if all the α’s are strictly
positive. We need now to obtain the coefficients of
the characteristic polynomial of the system defined as
D(s) = |sI − J|
= a
0
s
5
+ a
1
s
4
+ a
2
s
3
+ a
3
s
2
+ a
4
s +
a
5
, (55)
where I is the 5 × 5 identity matrix, and J represents
the Jacobian of the original system, Eq. (6), and de-
fined as
J(x) =
∂ ˙x
1
∂x
1
∂ ˙x
1
∂x
2
∂ ˙x
1
∂x
3
∂ ˙x
1
∂x
4
∂ ˙x
1
∂x
5
∂ ˙x
2
∂x
1
∂ ˙x
2
∂x
2
∂ ˙x
2
∂x
3
∂ ˙x
2
∂x
4
∂ ˙x
2
∂x
5
∂ ˙x
3
∂x
1
∂ ˙x
3
∂x
2
∂ ˙x
3
∂x
3
∂ ˙x
3
∂x
4
∂ ˙x
3
∂x
5
∂ ˙x
4
∂x
1
∂ ˙x
4
∂x
2
∂ ˙x
4
∂x
3
∂ ˙x
4
∂x
4
∂ ˙x
4
∂x
5
∂ ˙x
5
∂x
1
∂ ˙x
5
∂x
2
∂ ˙x
5
∂x
3
∂ ˙x
5
∂x
4
∂ ˙x
5
∂x
5
=
0 1 0 0 0
0 b
22
b
23
b
24
0
0 0 b
33
b
34
0
0 0 0 0 1
b
51
b
52
b
53
b
54
b
55
, (56)
where the coefficients of the Jacobian are as
b
22
= a
5
+ 2a
6
x
2
b
23
= 2x
3
(a
1
+ a
2
x
4
−
√
a
3
+ a
4
x
4
)
b
24
= x
2
3
a
2
−
a
4
2
√
a
3
+ a
4
x
4
b
33
= a
8
+ 2a
10
x
3
sin x
4
+ 2a
9
x
3
+
∂u
1
∂x
3
b
34
= a
10
x
2
3
cos x
4
+
∂u
1
∂x
4
b
51
=
∂u
2
∂x
1
(57)
b
52
=
∂u
2
∂x
2
b
53
= 2a
14
x
3
sin x
4
+
∂u
2
∂x
3
b
54
= a
13
+ a
14
x
2
3
cos x
4
+
∂u
2
∂x
4
b
55
= a
15
,
Recalling that there are two possibilities for the con-
trol law, as seen by the duality of u
1
, Eqs. (50) and
(51), there are also two possibilities for
∂u
1
∂x
3
and
∂u
1
∂x
4
as seen bellow,
∂u
1
(x
3
D
)
∂x
3
=
∂u
1
(x
4
D
)
∂x
3
= −b
3
∂u
1
(x
3
D
)
∂x
4
= −
a
7
cos x
4
(a
1
+ a
2
x
4
D
−
√
a
3
+ a
4
x
4
D
)c
7
∂u
1
(x
4
D
)
∂x
4
= 0.
The partial derivatives of the control law Eq. (43) are
∂u
2
∂x
1
= 4K
f
c
8
1 +
1
1 − 4c
8
(K
a
− v)
∂v
∂x
1
∂u
2
∂x
2
= 4K
f
c
8
1 +
1
1 − 4c
8
(K
a
− v)
∂v
∂x
2
∂u
2
∂x
3
= 4K
f
c
8
1 +
1
1 − 4c
8
(K
a
− v)
∂v
∂x
3
+
2K
h
x
3
sin x
4
∂u
2
∂x
4
= K
h
x
2
3
cos x
4
,
where the partial derivatives of v with respect to the
states are defined as
∂v
∂x
1
= −
b
1
x
2
3
∂v
∂x
2
= −
2a
6
x
2
+ d
x
2
3
(58)
∂v
∂x
3
=
2a
6
x
2
2
+ 2a
7
+ 2dx
2
+ 2b
1
(x
1
− x
1
D
)
x
2
3
.
Substituting Eq. (56) into (55), yields the coefficients
of the characteristic polynomial
a
0
= 1
a
1
= −b
33
− b
22
− b
55
a
2
= −b
54
+ b
22
b
55
+ b
22
b
33
+ b
33
b
55
a
3
= −b
22
b
33
b
55
+ b
33
b
54
+ b
22
b
54
− b
52
b
24
−
b
53
b
34
(59)
a
4
= −b
52
b
23
b
34
− b
24
b
51
+ b
52
b
24
b
33
+
b
22
b
53
b
34
− b
22
b
33
b
54
a
5
= −b
51
(b
23
b
34
− b
33
b
24
).
Once the Jacobian is calculated, in order to proceed
with the stability analysis at the desired final con-
ditions, it is necessary to substitute the equilibrium
conditions. These conditions, as seen in section 2.1,
imply that the vertical velocity of the helicopter and
the rate of change of the collective pitch tend to zero
(x
2
= x
5
= 0), which simplifies substantially the
coefficients and the corresponding analysis. Also
when the system achieves the desired operating point,
x
1
= x
1
D
, x
2
= x
2
D
and x
3
= x
3
D
. Once
the equilibrium points are substituted, the coefficients
of the characteristic polynomial only depend on the
variation in x
3
D
and x
4
D
, and the final desired alti-
tude (x
1
D
) is irrelevant for the analysis. Figures 3
and 4 represents the variation of the coefficients of
the characteristic polynomial and the Routh-Hurwitz
coefficients respectively of the closed-loop system
as the desired collective pitch angle is varied from
14.3239
◦
> x
4
D
> 4.8727
◦
. Figures 5 and 6 repre-
sents the variation of the coefficients of the character-
istic polynomial and the Routh-Hurwitz coefficients
respectively of the closed-loop system as the desired
STABILITY ANALYSIS OF A THREE-TIME SCALE SINGULAR PERTURBATION CONTROL FOR A
RADIO-CONTROL HELICOPTER ON A PLATFORM
55

collective pitch angle is varied from 180 rads/sec>
x
4
D
> 52.3163 rads/sec, and it can be seen that for
both φ
1
and φ
2
all the coefficients of the characteristic
polynomial are greater than zero, and the the coeffi-
cients of the first column are positive thus all the roots
of the characteristic polynomial are negative and the
closed loop system is stable.
5 SIMULATION RESULTS
The simulations are conducted using a 4
th
Runge-
Kutta fixed step integration method with an integra-
tion step of 0.01 seconds. Only a representative of
the sensitivity analysis conducted will presented in
this article. For further details refer to the results pre-
sented in (Esteban et al., 2005). The sensitivity analy-
sis is conducted to variation in desired final values.
The initial conditions of the helicopter are kept con-
stant, x
1
(0) = 0.45m, x
2
(0) = 0.1 m/sec, x
3
(0) =
70 rads/sec, x
4
(0) = 0.1 rads and x
5
(0) = 0.5
rads/sec, while varying the desired final conditions,
x
1
D
and x
4
D
. Fig. 7 shows the simulation results
for desired final altitudes of 0m ≤ x
1
D
≤ 1.25m,
and Fig. 8 shows the simulation results for desired
final collective pitch angle of 0.075rads ≤ x
4
D
≤
0.2r ads. Fig. 7 is divided into four subfigures, where
from left to right and top to bottom represent the heli-
copter altitude, x
1
, angular velocity of the blades, x
3
,
collective pitch angle, x
4
, and both control signals, u
1
and u
2
. The control laws perform well and the states
are driven to the desired final states. A extended range
of initial conditions will be studied and presented on
the final version of this article.
6 CONCLUSION
The stability analysis conducted on the closed loop
system, for the control law, demonstrates the stability
of the control law which corroborates the results pre-
sented in (Esteban et al., 2005). The stability analy-
sis also demonstrates that both variants of the con-
trol law, depending on selecting x
3
D
or x
4
D
as one
of the desired final values, are stable. The study also
demonstrates that the stability and the effectiveness
of the control law has no dependence on the final de-
sired altitude (x
1
D
). Future work might include the
study of the actuators saturation and the robustness of
the control law to perturbations, both unmodeled dy-
namics and external disturbances. Future work will
also include the extension of this controller to a real
system Radio/Control helicopter model on a platform
similar to the one presented in this study.
ACKNOWLEDGMENTS
This work has been supported under MCyT-FEDER
grants DPI2003-00429 and DPI2001-2424-C02-01.
REFERENCES
Balakrishnan, S. N. and Huang, Z. (2001). Robust adap-
tive critic based neurocontrollers for helicopter with
unmodeled uncertainties. In 2001 AIAA Guidance,
Navigation and ControlConference, Montreal. AIAA.
paper 2001-4258.
Bugajski, D. J., Enns, D. F., and Elgersma, M. R. (1990).
A dynamic inversion based control law with applica-
tion to the high angle of attack research vehicle. In
Proceeding of The AIAA Guidance, Navigation, and
Control Conference, pages 20–22. AIAA.
Bull, J., Kaneshige, J., and Totah, J. (2000). Generic
neural flight control and autopilot system. In Proceed-
ings of the AIAA Guidance, Navigation and Control
Conference, Denver. AIAA. Article number AIAA-
2000-4281.
Calise, A. J., Corban, J. E., Pei, Y., and Prasad, J. V. R.
(1999). Adaptive nonlinear controller synthesis and
flight test evaluation on an unmanned helicopter. In
Proceedings to the IEEE International Conference on
Control Applications, pages 871–879. IEEE.
Curtis, H. C. (2003). Rotorcraft stability and control:
Past, present, and future. the 20th annual alexander a.
nikolsky lecture. Journal of the American Helicopter
Society, 48(1):3–11.
Esteban, S., Gordillo, F., and Aracil, J. (2005). Three-time
scale singular perturbation control for a radio-control
helicopter on a platform. In Proceedings of the AIAA
Guidance, Navigation, and Control Conference and
Exhibit, San Francisco, USA. AIAA.
Haley, P. and Soloway, D. (2001). Aircraft reconfiguration
using neural generalized predictive control. In Pro-
ceedings of the American Control Conference, pages
2294–2929, Arlington, VA. ACC.
Khalil, H. K. (1996). Nonlinear Systems. Prentice-Hall.
Kokotovi
´
c, P. V., Khalil, H. K., and O’Reily, J. (1986). Sin-
gular Perturbation Methods in Control: Analysis and
Design. Academon Press.
Lee, T. and Kim, Y. (2001). Nonlinear adaptive flight
control using backstepping and neural networks con-
troller. AIAA Journal of Guidance, Control, and Dy-
namics, 24(4):675–682.
Leiter, J., Calise, A. J., and Prasad, J. V. R. (1995). Analysis
of adaptive neural networks for helicopter flight con-
trol. In Proceeding of the AIAA Guidance, Navigation,
and Control Conference, pages 871–879. AIAA.
Meyer, G., Su, R., and Hunt, L. R. (1984). Application of
nonlinear transformations to automatic flight control.
In 1984 IFAC Congress. IFAC.
ICINCO 2005 - ROBOTICS AND AUTOMATION
56

Miniature-Aircraft-USA (1999). X-cell 50, technical
Manual. Technical report, Orlando, Fla.
Naidu, D. S. and Calise, A. J. (2001). Singular perturbations
and time scales in guidance and control of aerospace
systems: a survey. AIAA Journal of Guidance, Con-
trol, and Dynamics, 24(6):1057–1078.
Naidu, S. D. (2002). Singular perturbations and time
scales in control theory and applications: an overview.
In Dynamics of Continuous, Discrete and Impulsive
Systems Series B: Applications and Algorithms, vol-
ume 9, pages 233–278. Watom Press.
Pallet, T. J. and Ahmad, S. (1991). Real-time helicopter
flight control: Modelling and control. Technical report
tr-ee 91-35, school of electrical engineering, purdue
university.
Pallet, T. J., Wolfert, B. J., and Ahmad, S. (1991). Real
time helicopter flight control test bed. Technical report
tr-ee 91-28, school of electrical engineering, purdue
university.
Reiner, J., Balas, G. J., and Garrard, W. L. (1995). Robust
dynamic inversion for control of highly maneuverable
aircraft. AIAA Journal of Guidance, Control, and Dy-
namics, 18(1):18–24.
Routh, E. J. (1905). Dynamics of a System of Rigid Bodies.
Macmillan, London.
Sira-Ramirez, H., Zribi, M., and Ahmad, S. (1994). Dy-
namical sliding mode control approach for vertical
flight regulation in helicopters. In IEE Proceedings
on Control Theory and Applications, volume 141 Is-
sue 1, pages 19–24.
Snell, S. A., Enns, D. F., and Garrard, W. L. (1992). Non-
linear inversion flight control for a supermaneuverable
aircraft. AIAA Journal of Guidance, Control, and Dy-
namics, 15(4):976–984.
FIGURES
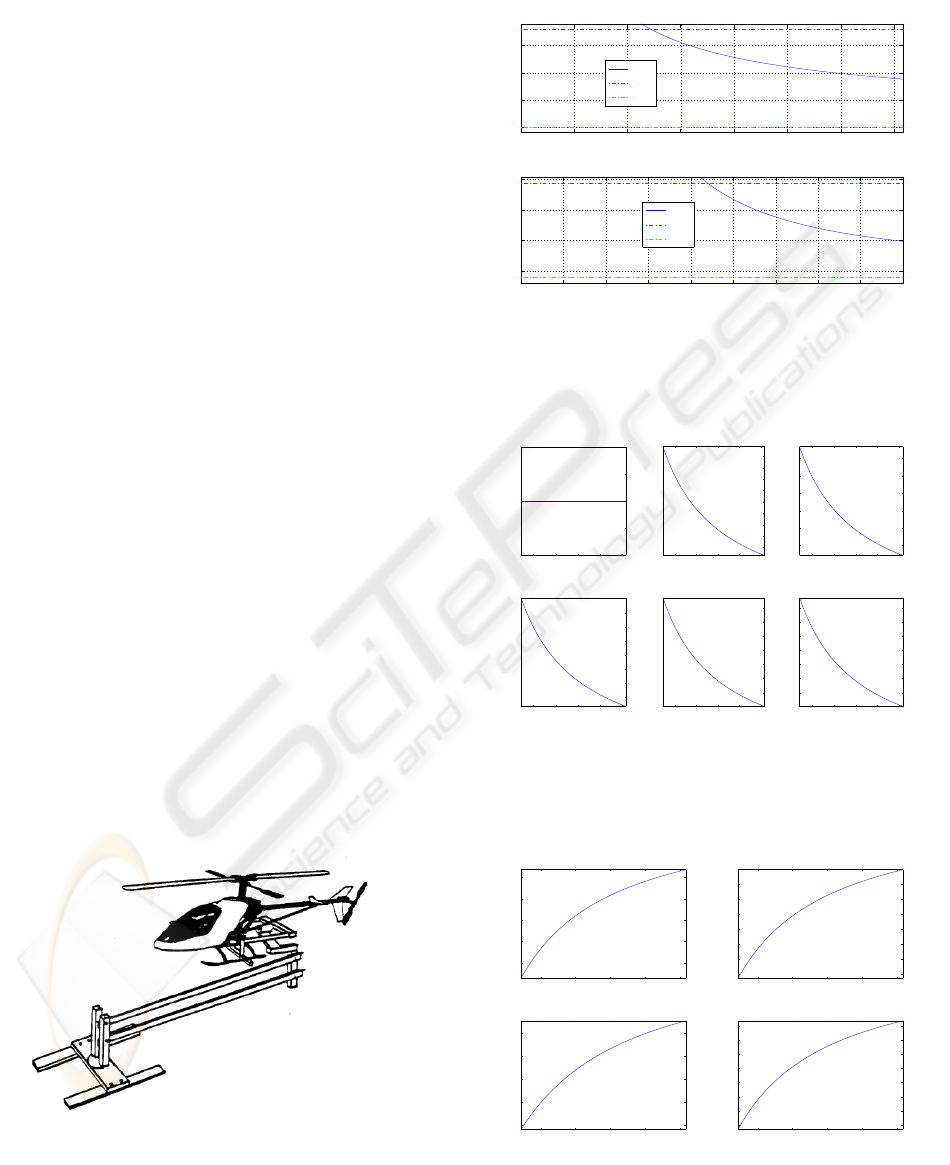
Figure 1: Helicopter mounted on a Stand (Pallet et al., 1991)
(Pallet and Ahmad, 1991)
2 4 6 8 10 12 14
0
50
100
150
x
4
D
− rads/sec
x
3
D
− degs
+φ
1
(x
4
D
)
0 20 40 60 80 100 120 140 160 180
0
5
10
15
x
3
D
− rads/sec
x
4
D
− degs
+φ
2
(x
3
D
)
+φ
1
(x
4
D
)
x
3
max
−x
3
max
+φ
2
(x
3
D
)
x
4
max
−x
4
max
Figure 2: Relation of φ
1
(x
4
D
) and φ
2
(x
3
D
).
6 8 10 12 14
0
0.5
1
1.5
2
s
0
6 8 10 12 14
67.45
67.5
67.55
67.6
67.65
67.7
67.75
67.8
67.85
s
1
6 8 10 12 14
960
965
970
975
980
985
s
2
6 8 10 12 14
2700
2750
2800
2850
2900
2950
3000
3050
s
3
x
4
− degs
6 8 10 12 14
2700
2750
2800
2850
2900
2950
3000
s
4
x
4
− degs
6 8 10 12 14
1900
1950
2000
2050
2100
2150
2200
s
5
x
4
− degs
Figure 3: Coefficients for φ
1
(x
4
D
).
6 8 10 12 14
830
835
840
845
850
Routh−Hurwitz Coefficients
B
1
6 8 10 12 14
1200
1250
1300
1350
1400
1450
1500
Routh−Hurwitz Coefficients
C
1
6 8 10 12 14
950
1000
1050
1100
1150
x
4
− degs
D
1
6 8 10 12 14
500
550
600
650
700
750
800
850
x
4
− degs
E
1
Figure 4: Routh-Hurwitz Coefficients for φ
1
(x
4
D
).
STABILITY ANALYSIS OF A THREE-TIME SCALE SINGULAR PERTURBATION CONTROL FOR A
RADIO-CONTROL HELICOPTER ON A PLATFORM
57

50 100 150 200
0
0.5
1
1.5
2
s
0
x
3
− rads/sec
50 100 150 200
67.2
67.3
67.4
67.5
67.6
67.7
67.8
67.9
68
s
1
x
3
− rads/sec
50 100 150 200
940
950
960
970
980
990
s
2
x
3
− rads/sec
50 100 150 200
2400
2500
2600
2700
2800
2900
3000
3100
s
3
x
3
− rads/sec
50 100 150 200
2400
2500
2600
2700
2800
2900
3000
s
4
x
3
− rads/sec
50 100 150 200
1600
1700
1800
1900
2000
2100
2200
s
5
x
3
− rads/sec
Figure 5: Coefficients for φ
2
(x
3
D
).
40 60 80 100 120 140 160 180
910
915
920
925
930
935
940
945
Routh−Hurwitz Coefficients
B
1
x
3
− rads/sec
40 60 80 100 120 140 160 180
2200
2300
2400
2500
2600
2700
2800
Routh−Hurwitz Coefficients
C
1
x
3
− rads/sec
40 60 80 100 120 140 160 180
1700
1800
1900
2000
2100
2200
2300
Routh−Hurwitz Coefficients
x
3
− rads/sec
D
1
40 60 80 100 120 140 160 180
1600
1700
1800
1900
2000
2100
2200
Routh−Hurwitz Coefficients
x
3
− rads/sec
E
1
Figure 6: Routh-Hurwitz Coefficients for φ
2
(x
3
D
).
(a) x
1
(b) x
3
(c) x
4
(d) u
1
andu
2
Figure 7: States and Control Histories For Variable Desired
Final Altitude.
(a) x
1
(b) x
3
(c) x
4
(d) u
1
andu
2
Figure 8: States and Control Histories For Variable Desired
Final Collective Pitch Angle.
ICINCO 2005 - ROBOTICS AND AUTOMATION
58