COOPERATIVE MULTI-ROBOT LOCALIZATION: USING
COMMUNICATION TO REDUCE LOCALIZATION ERROR
Valguima Odakura, Anna Helena Reali Costa
Laborat
´
orio de T
´
ecnicas Inteligentes - LTI
Departamento de Engenharia de Computac
˜
ao e Sistemas Digitais - PCS
Escola Polit
´
ecnica da Universidade de S
˜
ao Paulo
Av. Luciano Gualberto, trav 3, n. 158
Cidade Universit
´
aria, S
˜
ao Paulo-SP, Brasil
Keywords:
autonomous systems, mobile robots, multi-robot localization, cooperative multi-robot.
Abstract:
This paper presents a statistical algorithm for cooperative multi-robot localization based on a propagating
detection model. The problem of multi-robot localization consists of localizing each robot in a group within
the same environment, when robots share information to improve localization accuracy. Our approach is based
on a well-known probabilistic localization approach, the Markov localization, that was originally designed to
a single robot. A detection model can be incorporated in order to accommodate multi-robot cooperation in
Markov localization. In this model, two robots exchange their pose beliefs whenever one robot detects another.
We propose a novel detection model in that all robots in the group can benefit from a meeting of two robots
through detection propagation. The technique has been implemented and tested in simulated environments.
Experiments illustrate improvements in localization accuracy when compared with a previous multi-robot
localization approach.
1 INTRODUCTION
Localization is one of the main abilities of an au-
tonomous mobile robot. In order to perform their
tasks, mobile robots need to know their pose, posi-
tion (x, y) and heading θ, as accurate as possible. It is
a challenging task, once localization is based on sen-
sors readings, which are uncertain and noisy. Because
of that, most of the robot localization approaches are
based on probabilistic methods. In order to accom-
plish tasks more quickly and robustly than a single
robot, multiple robots can be used (Cao et al., 1997;
Parker, 2000), which poses the multi-robot localiza-
tion problem.
The multi-robot localization problem consists of
localizing each robot in a group within the same envi-
ronment. It can be performed in two manners. Firstly,
it can be done individually, where each robot solves
its self-localization problem alone, based on its own
resources. Secondly, it can be performed coopera-
tively, which takes advantage of multiple robots to
improve positioning accuracy beyond what is possi-
ble with a single robot. In the latter case, coopera-
tion is achieved by communication. The key idea of
cooperation in multi-robot localization is that each ro-
bot can use measurements taken by all robots, in order
to better estimates its own pose. In this way, the main
difference between single robot and cooperative mul-
tiple robots localization is that multi-robot can have
more information than single robot.
The information communicated by robots can be
guided by robots detections, as in Roumeliotis and
Bekey (2002) and Fox et al. (2000). Every time one
robot detects another, they communicate and share
their pose beliefs. In Fox et al. (2000), detection
model performs pose update only for the two meeting
robots. We argue that this information can be shared
among all robots in the group, improving localization
accuracy of all robots. Thus, the goal of this paper
is to present an algorithm to multi-robot localization,
based on a novel detection model that propagates a
detection to all robots within a group.
The cooperative multi-robot localization problem
addressed in this paper considers the following as-
sumptions:
• Initial robots’ poses are unknown.
• Robots know an environment model.
• Robots are equipped with proprioceptive sensors
that measure their self-motion.
• Robots are equipped with exteroceptive sensors
that monitor the environment, and detect and iden-
tify other robots.
• Robots are equipped with communication devices
that allow them to exchange information.
This paper is organized as follows. In Section 2, the
single robot localization problem is presented and the
88
Odakura V. and Helena Reali Costa A. (2005).
COOPERATIVE MULTI-ROBOT LOCALIZATION: USING COMMUNICATION TO REDUCE LOCALIZATION ERROR.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 88-93
DOI: 10.5220/0001190600880093
Copyright
c
 SciTePress

Markov localization technique is introduced. In Sec-
tion 3 the localization problem is extended to a group
of robots. The proposed detection model to improve
multi-robot localization accuracy is described in Sec-
tion 4. Experiments realized are shown in Section 5.
Finally, in Section 6, our conclusions are derived and
future works are presented.
2 LOCALIZATION APPROACHES
Mobile robot localization is the problem of estima-
ting a robot pose within an environment based on ob-
servations. Observations consist of information about
the robot’s movement and about the environment. In-
formation provided by sensors are inherently uncer-
tain, so probabilistic techniques are needed to deal
with this.
The probabilistic approach uses a probabilistic re-
presentation of the robot’s pose, that is, robot’s pose
is modeled by a random variable and the state space
of this variable consists of all the poses within the en-
vironment. In this context, mobile robot localization
can be classified as local or global. In local local-
ization, the probability distribution function used is
a unimodal Gaussian. In consequence of this rep-
resentation, the pose of the robot is assumed to be
within a small area and the initial robot’s pose has
to be known. In global localization, robot’s pose
is represented by a multi-modal probability distribu-
tion, which allows determining robot’s pose without
knowledge of its initial pose.
Most approaches of local localization use Kalman
filter to determine the pose of robots. In the Kalman
filter approach, the robot’s pose is described by using
a Gaussian distribution. The Kalman filter technique
has been shown to be accurate for keeping tracking of
robot’s pose (Leonard and Durrant-Whyte, 1991).
A global localization approach is ML – Markov
localization. This localization technique maintains
a probability distribution over the space of all poses
of a robot in its environment, so it deals with multi-
modal distributions. Markov localization relies on
the Markov assumption, which states that past sen-
sor readings are conditionally independent of future
readings, given the true pose of the robot, (Fox et al.,
1999).
In ML, p(x
t
= x) denotes the robot’s belief that
it is at pose x at time t, where x
t
is a random vari-
able representing the robot’s pose at time t, and x =
(x, y, θ) is the pose of the robot. This belief represents
a probability distribution over all the space of x
t
.
ML uses two models to localize a robot: a mo-
tion model and an observation model. The motion
model is specified as a probability distribution p(x
t
=
x|x
t−1
= x
′
, a
t−1
), where x
t
is a random variable
representing the robot’s pose at time t, a
t
is the action
or movement executed by the robot at time t. The
movement can be estimated, for example, by odome-
ters on the wheels. The observation model is used to
incorporate information from exteroceptive sensors,
such as proximity sensors and camera, and it is ex-
pressed as p(x
t
= x|o
t
), where o
t
is an observation
sensed at time t.
In ML the motion model is described as:
p(x
t
= x|x
t−1
= x
′
, a
t−1
) =
X
x
′
p(x
t
= x|x
t−1
= x
′
, a
t−1
)p(x
t−1
= x
′
), (1)
where p(x
t
= x|x
t−1
= x
′
, a
t−1
) is characterized by
a normal distribution:
p(x
t
= x|x
t−1
= x
′
, a
t−1
) =
1
σ(a
t−1
)
√
2π
exp −
(|x − x
′
| − a
t−1
)
2
2σ
2
(a
t−1
)
, (2)
where σ(a
t−1
) is the standard deviation given a
t−1
.
The observation model is described as:
p(x
t
= x|o
t
) =
p(o
t
|x
t
= x)p(x
t
= x)
P
x
′
p(o
t
|x
t
= x
′
)p(x
t
= x
′
)
,
(3)
where p(o
t
|x
t
= x) is characterized by a normal dis-
tribution. For a proximity sensor:
p(o
t
|x
t
= x) =
1
σ(o
t
)
√
2π
exp −
(d − o
t
)
2
2σ
2
(o
t
)
, (4)
where d is the measured distance if the sensor detects
an obstacle, o
t
is the distance to the next obstacle in
the map, and σ(o
t
) is the standard deviation given o
t
.
The Markov localization algorithm is presented in
Algorithm 1. In the beginning, p(x
0
= x) is the prior
belief about the initial pose of the robot. If the initial
pose is unknown, p(x
0
= x) is uniformly distributed
around all possible poses.
In the next section, the multi-robot localization
problem is presented based on the Markov localiza-
tion approach.
3 MULTI-ROBOT
LOCALIZATION
The cooperative multi-robot localization problem
consists of localizing each robot in a group within the
same environment, when robots share information in
order to improve localization accuracy.
Representative recent works in cooperative multi-
robot localization are from Roumeliotis and Bekey
(2002) and Fox et al. (2000), that use Kalman Filter
and Particle Filter as algorithms, respectively.
COOPERATIVE MULTI-ROBOT LOCALIZATION: USING COMMUNICATION TO REDUCE LOCALIZATION
ERROR
89

Algorithm 1 Single Robot Markov Localization
Fox et al. (1999)
for each pose x do
Initialize p(x
0
= x)
end for
loop
if robot receives an odometer reading then
for each pose x do
p(x
t
= x|x
t−1
= x
′
, a
t−1
) =
x
′
p(x
t
= x|x
t−1
= x
′
, a
t−1
)p(x
t−1
= x
′
)
end for
end if
if robot receives a sensor reading then
for each pose x do
p(x
t
= x|o
t
) =
p(o
t
|x
t
= x)p(x
t
= x)
x
′
p(o
t
|x
t
= x
′
)p(x
t
= x
′
)
end for
end if
end loop
The Markov localization (Fox et al., 1999) was ini-
tially designed for a single robot. One extension of
this work, aimed to solve the multi-robot problem is
presented in Fox et al. (2000). In order to accommo-
date multi-robot cooperation in Markov localization it
is necessary to add a detection model to the previous
observation and motion models.
The detection model (Fox et al., 2000) is based on
the assumption that each robot is able to detect and
identify other robots and furthermore, the robots can
communicate their probabilities distributions to other
robots. Let’s suppose that robot m detects robot n and
measures the relative distance between them, so:
p(x
n
= x|x
m
= x
′
, r
m
) = p(x
n
= x)
X
x
′
p(x
n
= x|x
m
= x
′
, r
m
)p(x
m
= x
′
), (5)
where x
n
represents the pose of robot n, x
m
repre-
sents the pose of robot m and r
m
denotes the
measured distance between robots. The calculation
P
x
′
p(x
n
= x|x
m
= x
′
, r
m
)p(x
m
= x
′
) describes
the belief of robot m about the pose of robot n. Si-
milarly, the same detection can be used to update the
pose of robot m.
The probability distribution p(x
n
= x|x
m
=
x
′
, r
m
) is characterized by a normal distribution. For
a proximity sensor:
p(x
n
= x|x
m
= x
′
, r
m
) =
1
σ(r
m
)
√
2π
exp −
(|x − x
′
| − r
m
)
2
2σ
2
(r
m
)
, (6)
where r
m
is the measured distance when robot m
detects robot n and σ(r
m
) is the standard deviation
given r
m
.
Once a detection is made according to the detection
model, the two robots involved in the process share
their probabilities distributions and relative distance.
This communication significantly improves the loca-
lization accuracy, if compared with a less communica-
tive localization approach.
The multi-robot localization algorithm proposed by
Fox et al. (2000) presents the advantage of performing
global localization (see algorithm 2). Robots in the
group cooperate to find their poses, communicating
their pose beliefs when they meet. One disadvantage
of this approach is that this information is shared only
by the two meeting robots and it is not used by the
other robots in the group.
A different detection model is presented by
Roumeliotis and Bekey (2002). Every time two ro-
bots meet, their meeting is used not only to update
their poses, but also to propagate to all robots in the
group. So, robots pose are estimated with all infor-
mation available at all time. However, the work uses
Kalman filter as localization technique, and is unable
to perform global localization.
The work presented in this paper aims at combining
the advantages of the previous works, in the way that:
(1) it can localize robots with unknown initial poses,
as Fox et al. (2000) and (2) communication is used
to propagate the information derived from a meeting
of two robots to the other robots in the group, so be-
coming similar to the work of Roumeliotis and Bekey
(2002). In order to achieve this goal, a new detection
model is presented in the next section.
4 DETECTION MODEL
In this section it is explained the communication
structure proposed to the detection model of multi-
robot localization. We share the motivation from Fox
et al. (2000) to investigate how localization accuracy
can be improved exploring shared information among
robots. However, we argue that all the robots in a
group (bigger than two robots) can benefit from the
shared information derived from a single detection
(when robot m meets robot n). Two questions raise:
What information is useful for non-meeting robots?
How can this information be shared?
Suppose a robot k in the group. When robot m
meets robot n, robot k can conclude that its pose is
not the robot m and n poses, once only one robot can
occupy the same space in the environment at the same
time. Robot k can also conclude that its pose is not in
the way between the two meeting robots, otherwise,
robot m would have detected robot k instead of robot
n. It is supposed that the detection sensor can sense
robots in front of the detecting robot. For example,
the detection sensor could be a camera (pointing for-
ICINCO 2005 - ROBOTICS AND AUTOMATION
90

ward) to identify the robot and a proximity sensor to
measure the distance.
The answer to the second question is to propagate
the probabilities distributions of the two meeting ro-
bots to the other robots in the group. It can be per-
formed by the robot m, that executes the detection.
When robot n updates its pose based on the informa-
tion communicated by robot m, it communicates back
its updated probability distribution, p
n
. Robot m then
calculates a probability distribution that will be com-
municated to the non-meeting robots:
p
d
(x
k
= x
′′
) = (1 − (p
m
(x
m
= x
′
)+
p
mn
(x
m
= x
′
, x
n
= x) + p
n
(x
n
= x))), (7)
where p
d
(x
k
= x
′′
) is the information communicated
to the non-meeting robots, p
m
(x
m
= x
′
) is the pro-
bability distribution of robot m, p
n
(x
n
= x) is the
probability distribution of robot n and p
mn
(x
m
=
x
′
, x
n
= x) is the probability distribution of a robot
being in the way between the two meeting robots (see
algorithm 3).
Figure 1 illustrates an example of this situation. In
the example there are 3 robots, R1, R2, R3 in their
actual poses. The robots have different knowledge
about their poses: robot 1 is certain about its pose, ro-
bot 2 is completely uncertain and robot 3 is in doubt
about 2 poses. The belief of robot 3 is represented
by the shaded cells. If robot 1 meets robot 2, robot 2
becomes certain about its pose and robot 3 keeps its
previous pose knowledge. However, if the detection
information is shared with robot 3, it becomes cer-
tain about its pose, because the possibility of being
between robot 1 and robot 2 is eliminated.
R1 R2
R3
Figure 1: Example: poses of 3 robots. R1 is certain about its
pose, R2 is completely uncertain and R3 is in doubt about
its pose (the two dashed cells).
The example shows the improvement in group
localization obtained if a detection information is
propagated to all robots in the group. This new com-
munication allows better localization results than in
Fox et al. (2000). Experimental results presented in
the next section allow comparative analysis.
Algorithm 2 Multi-robot Markov Localization
Fox et al. (2000)
for each robot x
m
do
for each pose x do
Initialize p(x
0
= x)
end for
loop
if robot receives an odometer reading then
for each pose x do
p(x
t
= x|x
t−1
= x
′
, a
t−1
) =
x
′
p(x
t
= x|x
t−1
= x
′
, a
t−1
)p(x
t−1
= x
′
)
end for
end if
if robot receives a sensor reading then
for each pose x do
p(x
t
= x|o
t
) =
p(o
t
|x
t
= x)p(x
t
= x)
x
′
p(o
t
|x
t
= x
′
)p(x
t
= x
′
)
end for
end if
if robot m detects robot n then
for each pose x do
p(x
n
= x|x
m
= x
′
, r
m
) = p(x
n
= x)
x
′
p(x
n
= x|x
m
= x
′
, r
m
)p(x
m
= x
′
).
end for
for each pose x do
p(x
m
= x|x
n
= x
′
, r
m
) = p(x
m
= x)
x
′
p(x
m
= x|x
n
= x
′
, r
m
)p(x
n
= x
′
).
end for
end if
end loop
end for
5 EXPERIMENTS
In order to evaluate the localization results obtained
with the cooperative multi-robot localization ap-
proach proposed in this paper we perform some ex-
periments. We compare our approach (algorithm 3)
to a previous approach (algorithm 2). In all experi-
ments our approach outperforms the algorithm 2.
The experiments are conducted with simulated ro-
bots. Each robot is equipped with a proximity sensor
to measure the distance to the walls in the environ-
ment, and a detection sensor, that can identify other
robots and measure their relative position (x, y). All
robot sensors are assumed to be corrupted by gaussian
noise. The robots know an environment model and
they do not know their initial poses in the environ-
ment. All the robots move simultaneously through
the environment and they keep moving until all robots
find their poses, that is, until their localization errors
become near zero.
COOPERATIVE MULTI-ROBOT LOCALIZATION: USING COMMUNICATION TO REDUCE LOCALIZATION
ERROR
91

Algorithm 3 Novel Multi-robot Markov
Localization
for each robot x
m
do
for each pose x do
Initialize p(x
0
= x)
end for
loop
if robot receives an odometer reading then
for each pose x do
p(x
t
= x|x
t−1
= x
′
, a
t−1
) =
x
′
p(x
t
= x|x
t−1
= x
′
, a
t−1
)p(x
t−1
= x
′
)
end for
end if
if robot receives a sensor reading then
for each pose x do
p(x
t
= x|o
t
) =
p(o
t
|x
t
= x)p(x
t
= x)
x
′
p(o
t
|x
t
= x
′
)p(x
t
= x
′
)
end for
end if
if robot m detects robot n then
for each pose x do
p(x
n
= x|x
m
= x
′
, r
m
) = p(x
n
= x)
x
′
p(x
n
= x|x
m
= x
′
, r
m
)p(x
m
= x
′
).
end for
for each pose x do
p(x
m
= x|x
n
= x
′
, r
m
) = p(x
m
= x)
x
′
p(x
m
= x|x
n
= x
′
, r
m
)p(x
n
= x
′
).
end for
for each robot k but robot m and n do
for each pose x do
p(x
k
= x) =
x
′′
p(x
k
= x)p
d
(x
k
= x
′′
).
end for
end for
end if
end loop
end for
Tests are performed in two different environments.
The first environment is shown in Figure 2. It is a
symmetric hallway, similar to that used in Fox et al.
(2000). Since this environment is symmetric, robots
need to deal with ambiguities to be able to localize
themselves. For example, a single robot with un-
known initial pose, has to pass the open space on cor-
ridor A, or it has to pass through all other corridors,
B, C and D, in order to uniquely determine its pose.
A
D
B
C
Figure 2: Test 1: Symmetric hallway environment with 4
corridors denoted by A, B, C and D. Black represents obs-
tacles and walls and white represents free space.
The environment has dimensions 12 × 12 meters.
The robot environment model is a grid-based model,
where each cell has dimensions of 1 × 1 meters, and
angular resolution of 90 degrees. It results in a state
space of dimension 12 × 12 × 4 = 576 states. Expe-
riments are conducted with 8 robots, moving simul-
taneously through the corridors. All the robots run
clockwise, following the corridors.
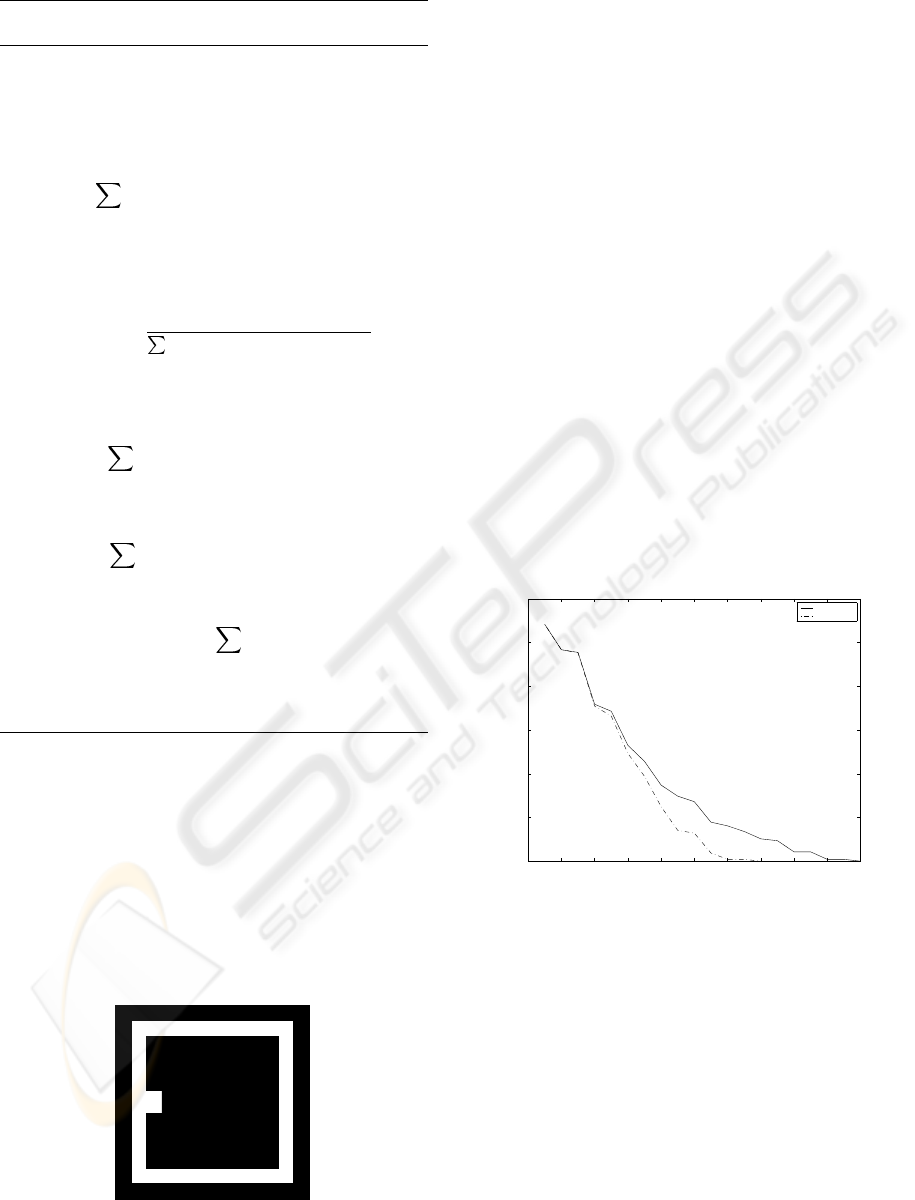
Figure 3 presents the localization errors per dis-
tance travelled for both methods. Results are avera-
ged by eight runs of the experiment. The solid line
refers to the algorithm 2 and the dashed line refers to
our algorithm. Initially all robots are uncertain about
their poses and their localization errors are high. As
they move, they become more certain about their ac-
tual pose, so their localization errors diminish. For
the algorithm 3, at distance 12 meters all robots are
certain about its poses, whereas for the algorithm 2 it
takes 18 meters.
Another measurement from the experiments is the
average distance travelled by all the robots over the
eight runs until they find their poses. It is 10.08 ±
1.32 meters for the algorithm 2 and 7.95 ± 1.14 for
algorithm 3. It is clear that our algorithm presents
smaller localization errors and distance travelled than
the other approach.
0 2 4 6 8 10 12 14 16 18 20
0
50
100
150
200
250
300
Distance (meters)
Localization error (meters)
Algorithm2
Algorithm3
Figure 3: Localization error: the distance travelled by the
robots until their localization errors are reduced to (near)
zero (x-axis) per the average localization error (y-axis).
The second environment used for tests is shown in
Figure 4. The environment is different from the first
one, once it is an open area, and the trajectories of
the robots are not restricted to follow a corridor. The
environment has dimensions 11 × 11 meters. The ro-
bot environment model is a grid-based model, where
each cell has dimensions of 1 ×1 meters, and angular
resolution of 90 degrees. It results in a state space of
dimension 11×11×4 = 484 states. Experiments are
conducted with four robots, performing random walk
through the environment.
Figure 5 presents the localization errors per dis-
tance travelled for both methods. Results are avera-
ICINCO 2005 - ROBOTICS AND AUTOMATION
92

Figure 4: Test 2: Open environment.
ged by eight runs of the experiment. The solid line
refers to the algorithm 2 and the dashed line refers to
our algorithm. Initially all robots are uncertain about
their poses and their localization errors are high. As
they move, they become more certain about their ac-
tual pose, so their localization errors diminish. For
the algorithm 3, at distance 20 meters all robots are
certain about its poses, whereas for the algorithm 2 it
takes 30 meters.
Another measurement from the experiments is the
average distance travelled by all the robots over the
eight runs until they find their poses. It is 12.56 ±
0.95 meters for the algorithm 2 and 11.44 ± 0.16 for
algorithm 3. It is clear that our algorithm presents
smaller localization errors and distance travelled than
the other approach.
0 5 10 15 20 25 30 35
0
100
200
300
400
500
600
Distance (meters)
Localization error (meters)
Algorithm2
Algorithm3
Figure 5: Localization error: the distance travelled by the
robots until their localization errors are reduced to (near)
zero (x-axis) per the average localization error (y-axis).
6 CONCLUSION AND FUTURE
WORK
We have presented a statistical approach for coope-
rative multi-robot localization. The experimental re-
sults demonstrate that our approach, when compared
to a previous multi-robot localization method, reduces
the uncertainty in localization significantly and re-
duces the distance travelled by the robots in order to
find their poses.
A limitation of our work is the increase in the
amount of data needed to communicate in order to
update robots’ poses. Thus, in future work, we are
interested in exploring the tradeoff between commu-
nication and localization accuracy.
Another point to be explored is an active detec-
tion approach. It means that when a robot knows its
pose it can communicate it to all the robots within the
group, and they can look for the right robot in order to
exchange pose information with it and improve their
pose beliefs.
A computationally efficient version of ML is the
Particle Filter – PF (Thrun et al., 2001). As shown
in Fox et al. (2000), Markov localization can be ex-
tended to PF. So, we pretend to extend the localization
approach proposed here to perform PF localization.
ACKNOWLEDGMENTS
This work was supported by Fapesp grant 01/14246-
4, Capes grant BEX 0803/03-0 and Capes/Grices
grant 099/03.
REFERENCES
Cao, Y. U., Fukunaga, A. S., Kahng, A. B., and Meng, F.
(1997). Cooperative mobile robotics: antecedents and
directions. Autonomous Robots, 4:1–23.
Fox, D., Burgard, W., Kruppa, H., and Thrun, S. (2000). A
probabilistic approach to collaborative multi-robot local-
ization. Autonomous Robots, 8(3).
Fox, D., Burgard, W., and Thrun, S. (1999). Markov lo-
calization for mobile robots in dynamic environments.
Journal of Artificial Intelligence Research, 11:391–427.
Leonard, J. and Durrant-Whyte, H. (1991). Mobile robot
localization by tracking geometric beacons. IEEE Trans-
actions on Robotics and Automation, 7(3):376–382.
Parker, L. E. (2000). Current state of the art in distributed
autonomous mobile robots. Distributed Autonomous Ro-
botic Systems, 4:3–12.
Roumeliotis, S. I. and Bekey, G. A. (2002). Distributed
multirobot localization. IEEE Transactions on Robotics
and Automation, 18(2):781–795.
Thrun, S., Fox, D., Burgard, W., and Dellaert, F. (2001).
Robust Monte Carlo localization for mobile robots. Arti-
ficial Intelligence, 128:99–141.
COOPERATIVE MULTI-ROBOT LOCALIZATION: USING COMMUNICATION TO REDUCE LOCALIZATION
ERROR
93