VERIFICATION OF TIMED CHI MODELS USING UPPAAL
E.M. Bortnik, D.A. van Beek, J.M. van de Mortel-Fronczak, J.E. Rooda
Department of Mechanical Engineering, Eindhoven University of Technology
P.O.Box 513, 5600 MB Eindhoven, The Netherlands
Keywords:
Discrete-event systems, process algebra, timed automata, performance analysis, functional analysis, verifica-
tion.
Abstract:
Due to increasing system complexity and growing competition and costs, powerful techniques are needed to
design and analyze manufacturing systems. One of the most popular techniques to do performance analysis is
simulation. However, simulation-based analysis cannot guarantee the correctness of a system. Our research
focuses on examining other methods to make performance analysis and functional analysis, and combining the
two. One of the approaches is to translate a simulation model that is used for performance analysis to a model
written in an input language of an existing verification tool. The process algebraic language χ is intended
for modeling, simulation, verification and real-time control and has been used extensively to simulate large
manufacturing systems. UPPAAL is an integrated tool environment for modeling, validation and verification
of real-time systems and has been applied successfully in case studies ranging from communication protocols
to multimedia applications. In this paper, we represent a translation scheme that is used to translate simulation
models written in χ language to UPPAAL timed automata and show a small example of the translation. Future
work includes defining an equivalence relation between χ and UPPAAL transition systems, implementing the
translator as a part of the χ toolset, and applying it for verification of models of manufacturing systems.
1 INTRODUCTION
Nowadays, due to increasing system complexity and
growing competition and costs, industry makes high
demands on powerful tools and techniques used to de-
sign and analyze manufacturing systems. One of the
most popular techniques to make performance analy-
sis is simulation. However, simulation-based analy-
sis becomes insufficient since it cannot guarantee the
correctness of a system. The objective of the TIPSy
project
1
(Tools and Techniques for Integrating Perfor-
mance Analysis and System Verification) is to com-
bine performance and functional analysis, particulary
in the χ environment.
The χ language is intended for modeling, simula-
tion, verification, and real-time control of manufac-
turing systems (van Beek et al., 2004). It is used
to model and simulate discrete-event, continuous or
combined, so-called hybrid, systems. The χ lan-
guage has a formal semantics which makes it suit-
1
supported by the Dutch Organization for Scientific Re-
search (NWO), project number 612.064.205
able for verification. The language and simulator have
been successfully applied to a large number of indus-
trial cases, such as an integrated circuit manufactur-
ing plant, a brewery and process industry plants (van
Beek et al., 2002).
Since we do not expect that a dedicated verification
tool for χ, that would be able to compete with exist-
ing optimized model checkers, could be built within
reasonable time, our aim is to translate χ models to
input languages of existing verification tools.
As the first step, a simple but representative model
was manually translated to µCRL, Promela and UP-
PAAL timed automata, and verified in CADP, Spin
and UPPAAL, respectively (Bortnik et al., 2005). In
this paper, a general translation scheme from a subset
of χ to UPPAAL is described. Using the scheme, the
χ toolset will be extended with the translator to make
possible to verify χ models in UPPAAL.
The related work includes (Nicollin et al., 1992),
where a process algebraic language is defined and
then translated into timed automata, and (Daws
et al., 1995), where a subset of ET-LOTOS is trans-
lated into the KRONOS timed automata. The simi-
486
M. Bortnik E., A. van Beek D., M. van de Mortel-Fronczak J. and E. Rooda J. (2005).
VERIFICATION OF TIMED CHI MODELS USING UPPAAL.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 486-492
DOI: 10.5220/0001191204860492
Copyright
c
 SciTePress

lar, singleformalizm-multisolution, approach has been
used in (D’Argenio et al., 2001; Bohnenkamp et al.,
2003), where systems are modelled in stochastic
process algebraic language Modest.
UPPAAL is a tool for modeling, simulation, val-
idation and verification of real-time systems that
can be modeled as a collection of non-deterministic
processes with finite control structure and real-valued
clocks (Larsen et al., 1997; Yi et al., 1994). The UP-
PAAL model checking engine allows to verify prop-
erties that are expressed in the UPPAAL Requirement
Specification Language. This language is a subset of
timed computation tree logic (TCTL), where prim-
itive expressions are location names, variables, and
clocks from the modeled system.
The remainder of the paper is organized as follows.
In Section 2, the subset of χ to be translated is de-
scribed. Then, in Section 3, the formal definition of
UPPAAL timed automata is given. The translation is
defined in Section 4. In Section 5, an example of
the translation of a part of a manufacturing system is
shown and the properties which can be verified are de-
scribed. Finally, in Section 6, conclusions are drawn.
2 THE χ LANGUAGE
In order to model timed discrete-event systems only,
the hybrid χ language has been simplified, resulting
in timed χ (van Beek et al., 2005). In the remainder
of this paper, we refer to timed χ as χ. The set M of
χ models, that can be translated using this translation
scheme, consists of models M ∈ M, where M is of
the following form:
h disc s
1
, . . . , s
k
, chan h
1
, . . . , h
l
, s
1
= c
1
∧ · · · ∧ s
k
= c
k
| |[
V
disc a
1
, . . . , a
n
, a
1
= b
1
∧ · · · ∧ a
n
= b
n
| p
1
]|
|| . . .
|| |[
V
disc a
1
, . . . , a
m
, a
1
= b
1
∧ · · · ∧ a
m
= b
m
| p
r
]|
i ,
where s
1
, . . . , s
k
, a
1
, . . . , a
n
, and a
1
, . . . , a
m
denote
the global and local discrete variables, h
1
, . . . , h
l
de-
note the urgent channels, s
1
= c
1
∧ · · · ∧ s
k
= c
k
,
a
1
= b
1
∧ · · · ∧ a
n
= b
n
, and a
1
= b
1
∧ · · · ∧ a
m
= b
m
are initialization predicates that restrict the allowed
values of the variables initially, and || denotes the par-
allel composition operator. Parallel composition and
the variable scope operators are not allowed inside the
process terms p
i
, since a UPPAAL model is a collec-
tion of sequential processes (represented by UPPAAL
timed automata) working in parallel.
The set of inductively defined process terms P con-
sists of the following process terms: skip, multi-
assignment x
n
:= e
n
, send h!!e
n
and receive h??x
n
,
where x
n
and e
n
denote the vectors (x
1
, . . . , x
n
) and
(e
1
,. . . , e
n
), deadlock δ and inconsistent process term
⊥, delay ∆d, where d denotes a constant integer val-
ued expression, delay enabling process term [p], repe-
tition ∗p, sequential composition p; q, and alternative
composition p [] q. The detailed explanations can be
found in (van Beek et al., 2005).
Formally, the set P of process terms p ∈ P is de-
fined by:
p ::= skip | x
n
:= e
n
| h!!e
n
| h??x
n
| δ | ⊥
| ∆d | [p] | ∗p
| p; p | p
′
[] p
′
where p
′
can be any process term except ∗p and [∗p].
Note, that the process term q [] ∗p still can be trans-
lated, since ∗p can be rewritten as p;∗p. Similarly, the
process term [∗p] can be rewritten as [p]; ∗p.
3 UPPAAL TIMED AUTOMATA
In literature, several formal definitions of UPPAAL
timed automata can be found (Behrmann et al., 2004;
Bengtsson and Yi, 2004; Larsen et al., 1997; M
¨
oller,
2002; Yi et al., 1994). For the translation, the for-
mal description of M.O. M
¨
oller (M
¨
oller, 2002) has
been chosen, as it covers most of the features of UP-
PAAL timed automata that have been implemented in
the tool.
A UPPAAL timed automaton A is a tuple
hL, l
0
, E, V, C, Init, Inv, T
L
i, where L is a finite set
of locations, and l
0
is the initial location. The set
of the edges E is defined by E ⊆ L × G(C, V ) ×
Sync × Act × L, where G(C, V ) is the set of con-
straints allowed in guards, V denotes the set of inte-
ger variables, C denotes the set of real-valued clocks
(C ∩ V = ∅), and Sync is a set of synchronization
actions which includes actions, co-actions, and the in-
ternal τ
h
-action. An action send over a channel h is
denoted by h! and its co-action receive is denoted by
h?. The τ
h
-action is an internal action which can-
not synchronize and does not have a co-action. Act
is a set of assignment actions, which includes assign-
ments, clock resets and the τ
a
-assignment. The τ
a
-
assignment is an empty assignment, i.e. an assign-
ment that does not change the values of the vari-
ables. Init ⊆ Act is a set of assignments that as-
signs the initial values to variables. The function
Inv : L → Inv(C, V ) assigns an invariant to each lo-
cation. Inv(C, V ) is the set of invariants over clocks
VERIFICATION OF TIMED CHI MODELS USING UPPAAL
487

C and variables V . The function T
L
: L → {o, u, c}
assigns the type (ordinary, urgent or committed) to
each location. The system cannot delay if there is a
process in an urgent or committed location. The tran-
sitions via the outgoing edges of a committed location
have priority.
A network of timed automata NA is a tu-
ple h
A, l
0
, V
′
, C
′
, H, T
H
, Init
′
i, where A =
(A
1
, . . . , A
n
) is a vector of n timed automata A
i
=
hL
i
, l
0
i
, E
i
, V
i
, C
i
, Init
i
, Inv
i
, T
L
i
i, for 1 ≤ i ≤ n.
l
0
= (l
0
1
, . . . , l
0
n
) is the initial location vector, V
′
and
C
′
are the sets of global (shared) variables and clocks,
respectively, (V
′
∩ C
′
= ∅), and H is a set of chan-
nels (V
′
∩ H = ∅ and C
′
∩ H = ∅). The function
T
H
: H → {o, u} assigns the type (ordinary or ur-
gent) to each channel. In case H = ∅, function T
H
is
undefined and is then informally denoted by ∅. Init
′
is the set of assignments that assigns the initial values
to the global variables. The formal semantics of UP-
PAAL timed automata can be found in (M
¨
oller, 2002).
4 TRANSLATION SCHEME
For the purpose of translation we assume existence
of a set of model variables V, a set of communication
variables V
h
, and a set of clocks C, such that V ∩ V
h
=
∅, and C ∩ (V ∪ V
h
) = ∅. The set of clocks C is used
for the translation of the delay operator.
The translation of timed χ to UPPAAL timed au-
tomata is defined by the means of two translation
functions. Function T
M
: M → NA translates a χ
model M to a UPPAAL network of automata NA us-
ing function T : P → A
s
that translates a χ process
term p ∈ P to an extended timed automaton. The
definition of an extended timed automaton A
s
is
based on the definition of the UPPAAL timed automa-
ton, extended with two additional elements: A
s
=
hL, l
0
, E, V, V
h
, C, Init, Inv, T
L
, l
f
i, where V
h
⊆ V
h
denotes an additional set of variables, that is used for
the translation of communication actions, and l
f
de-
notes a final location. The final location l
f
∈ L ∪ {⊤},
where ⊤ denotes that there is no final location, and
Inv(l
f
) = true, T
L
(l
f
) = o for all l
f
∈ L, is used for
the translation of sequential and alternative composi-
tion operators.
4.1 Translation function T
M
The translation function T
M
translates a χ model M
of the form:
h disc s
1
, . . . , s
k
, chan h
1
, . . . , h
l
, s
1
= c
1
∧ · · · ∧ s
k
= c
k
| |[
V
disc a
1
, . . . , a
n
, a
1
= b
1
∧ · · · ∧ a
n
= b
n
| p
1
]|
|| . . .
|| |[
V
disc a
1
, . . . , a
m
, a
1
= b
1
∧ · · · ∧ a
m
= b
m
| p
r
]|
i ,
where we assume {s
1
, . . . , s
k
} ⊆ V, {a
1
, . . . , a
n
} ∪
. . . ∪ {a
1
, . . . , a
m
} ⊆ V, ({a
1
, . . . , a
n
} ∪ . . . ∪
{a
1
, . . . , a
m
}) ∩ {s
1
, . . . , s
k
} = ∅ and {h
1
, . . . , h
l
} ∩
(V ∪ V
h
∪ C) = ∅, to a network of UPPAAL timed au-
tomata NA = h
A, l
0
, V
′
, C
′
, H, T
H
, Init
′
i. The func-
tion T
M
is defined as follows:
T
M
(M ) = h
A,l
0
,V
′
,{time},{h
1
,. . . , h
l
},T
H
,Init
′
i,
where A = (A
1
, . . . , A
r
) is a vector of r timed au-
tomata A
i
= F(T (p
i
)), for 1 ≤ i ≤ r, and the func-
tion F : A
s
→ A transforms an extended automa-
ton into a UPPAAL timed automaton A
i
by remov-
ing the set of the global variables V
h
and the fi-
nal location l
f
; l
0
= (l
0
1
, . . . , l
0
r
) is a vector of the
initial locations l
0
i
of the automata A
i
, 1 ≤ i ≤ r;
V
′
= ∪
1≤i≤r
V
h
i
∪ {s
1
, . . . , s
k
}, where V
h
i
is the set
of communication variables of the automaton T (p
i
).
Since the channels h
1
, . . . , h
l
in the model M are ur-
gent, T
H
(h
j
) = u, 1 ≤ j ≤ l. Finally, Init
′
= {time :=
0, s
1
:= c
1
, . . . , s
k
:= c
k
}.
4.2 Translation function T
In this section, the translation function T (p) is de-
fined inductively.
4.2.1 Translation of the atomic process terms
Skip
The process term skip is an abbreviation for an
action predicate that can only perform an internal
action without changing the valuation.
T (skip) =
h {l
0
, l
1
}, l
0
, {hl
0
, true, τ
h
, τ
a
, l
1
i}
, ∅, ∅, ∅, ∅, Inv, T
L
, l
1
i,
where Inv(l
0
) = true, Inv(l
1
) = true, T
L
(l
0
) =
u, T
L
(l
1
) = o.
Multi-assignment
Multi-assignment x
n
:= e
n
, n ≥ 1 is an abbre-
viation for an internal action that changes the
values of the variables x
1
, . . . , x
n
to the values of
ICINCO 2005 - ROBOTICS AND AUTOMATION
488

expressions e
1
, . . . , e
n
.
T (x
n
:= e
n
) =
h {l
0
, l
1
}, l
0
, {hl
0
, true, τ
h
, {x
1
:= e
1
, . . . , x
n
:= e
n
}, l
1
i}
, ∅, ∅, ∅, ∅, Inv, T
L
, l
1
i,
where Inv(l
0
) = true, Inv(l
1
) = true, T
L
(l
0
) =
u, T
L
(l
1
) = o.
Send and Receive
Undelayable send and receive process terms h!!e
n
and h??x
n
denote undelayable sending of expres-
sions e
n
via channel h and undelayable receiving via
channel h into variables x
n
.
In UPPAAL the values are not transmitted via
a channel. Instead, additional shared variables
y
1
, . . . , y
n
are used. We assume existence of a bi-
jective function f
v
: H × N → V
h
that generates
unique names of the communication variables: y
i
=
f
v
(h, i), i ∈ [1, n].
T (h!!e
n
) =
h {l
0
, l
1
}, l
0
, {hl
0
, true, h!, {y
1
:= e
1
, . . . , y
n
:= e
n
}, l
1
i}
, ∅, {y
1
, . . . , y
n
}, ∅, ∅, Inv, T
L
, l
1
i,
where Inv(l
0
) = true, Inv(l
1
) = true, T
L
(l
0
) =
u, T
L
(l
1
) = o.
T (h??x
n
) =
h {l
0
, l
1
}, l
0
, {hl
0
, true, h?, {x
1
:= y
1
, . . . , x
n
:= y
n
}, l
1
i}
, ∅, {y
1
, . . . , y
n
}, ∅, ∅, Inv, T
L
, l
1
i,
where y
i
= f
v
(h, i), i ∈ [1, n], Inv(l
0
) =
true, Inv(l
1
) = true, T
L
(l
0
) = u, T
L
(l
1
) = o.
Deadlock
The deadlock process term cannot perform ac-
tions or delays but it is consistent. The corresponding
extended timed automata is
T (δ) = h{l
0
}, l
0
, ∅, ∅, ∅, ∅, ∅, Inv, T
L
, ⊤ i,
where Inv(l
0
) = true, T
L
(l
0
) = u.
Inconsistent process term
The inconsistent process term ⊥ is inconsistent
for all valuations and cannot perform any action or
delay. The corresponding extended timed automata is
T (⊥) = h{l
0
}, l
0
, ∅, ∅, ∅, ∅, ∅, Inv, T
L
, ⊤ i,
where Inv(l
0
) = false, T
L
(l
0
) = u.
4.2.2 Translation of the operators
In the translation of the operators, the extended au-
tomaton that is obtained by translating the process
term p ∈ P is denoted by T (p) = A
p
s
, where A
p
s
=
hL
p
, l
p
0
, E
p
, V
p
, V
hp
, C
p
, Init
p
, Inv
p
, T
p
L
, l
p
f
i. In a
similar way, A
q
s
denotes T (q).
For the translation some additional functions are
needed. The restriction of a function f : A → B to
C ⊆ A is denoted by f ↾ C. If f and g are functions
and dom(f) ∩ dom(g) = ∅, then f ∪ g denotes func-
tion h with the domain dom(h) = dom(f ) ∪ dom(g),
where h(c) = f (c) if c ∈ dom(f), and h(c) = g(c) if
c ∈ dom(g).
For arbitrary sets E, L, Act, where E is a set of
edges, L is a set of locations, and Act is a set of
assignments, two more functions are defined. Func-
tion γ : P(E) × L × P(Act) → P(E) transforms
the set of edges by adding a set of assignments to the
assignment part of all incoming edges of a location.
For instance, the function γ(E, l, {x := 1, y := 3})
returns a set of edges, where the set of assignments
{x := 1, y := 3} is added to the assignment parts
of all incoming edges of the location l. Function
σ : P(E) × L × L → P(E) transforms the set of edges
by replacing all occurrences of the first location with
the second one. For instance, the function σ(E, l, l
′
)
returns the set of edges, where all occurrences of the
location l are replaced with l
′
.
Variable scope operator
Local variables are introduced in a χ process by
means of the variable scope operator.
T (|[
V
disc a
1
, . . . , a
n
, a
1
= b
1
∧ · · · ∧ a
n
= b
n
| p
]| ) =
hL
p
, l
p
0
, E
p
, V
p
∪ {a
1
, . . . , a
n
}, V
hp
, C
p
, Init
p
∪ {a
1
:= b
1
, . . . , a
n
:= b
n
}, Inv, T
L
, l
p
f
i.
Delay operator
The abbreviation △d denotes a process term
that first delays for d time units, and then terminates
by means of an internal action τ.
To translate the delay operator, additional fresh
clock variables are used. We assume that a unique
name of the variable c ∈ C is generated by some bi-
jective function f
c
: L → C.
T (△d) =
h {l
0
, l
1
}, l
0
, {hl
0
, c == d, τ
h
, τ
a
, l
1
i}
, ∅, ∅, {c}, {c := 0}, Inv, T
L
, l
1
i,
VERIFICATION OF TIMED CHI MODELS USING UPPAAL
489

where c = f
c
(l
0
), Inv(l
0
) = (c ≤ d), Inv(l
1
) =
true, T
L
(l
0
) = o, T
L
(l
1
) = o.
Delay enabling operator
The delay enabling operator [p] allows time transi-
tions of arbitrary duration for the behavior of p. In
order to translate this operator, the initial position
of the extended automaton has to become delayable
(ordinary).
T ([p]) =
hL
p
, l
p
0
, E
p
, V
p
, V
hp
, C
p
, Init
p
, Inv, T
L
, l
p
f
i,
where Inv(l
p
0
) = true, T
L
(l
p
0
) = o, and ∀l
p
∈
L
p
\ {l
p
0
} : Inv(l
p
) = Inv
p
(l
p
), T
L
(l
p
) = T
p
L
(l
p
).
Repetition
Process term ∗p represents infinite repetition
of process term p. If the extended automaton
A
p
s
= T (p) has a final location (l
p
f
∈ L
p
), then the
incoming edges of the final location are redirected to
the initial location, and the initializations are added to
the assignment parts of these edges. If the extended
automaton A
p
s
does not have a final location (l
p
f
= ⊤),
then T (∗p) = A
p
s
. The resulting extended automaton
is defined in the following way.
T (∗p) =
hL, l
p
0
, E, V
p
, V
hp
, C
p
, Init
p
, Inv
p
↾ L, T
p
L
↾ L, ⊤
i
where if l
p
f
= ⊤, then L = L
p
, and E = E
p
, otherwise
L = L
p
\ {l
p
f
}, and E = σ(γ(E
p
, l
p
f
, Init
p
), l
p
f
, l
p
0
).
Sequential composition
The sequential composition of process terms p
and q behaves as process term p until p terminates,
and then continues to behave as process term q. If
the extended automaton A
p
s
has a final location, the
sequential composition p; q is translated by replacing
the final location l
p
f
of the extended automaton A
p
s
with the initial location l
q
0
of the extended automaton
A
q
s
in the following way.
T (p; q) =
h (L
p
\ {l
p
f
}) ∪ L
q
, l
p
0
, E, V
p
∪ V
q
, V
hp
∪ V
hq
, C
p
∪ C
q
, Init
p
, Inv, T
L
, l
q
f
i,
where E = σ(γ(E
p
, l
p
f
, Init
q
), l
p
f
, l
q
0
), and Inv =
(Inv
p
↾ (L
p
\ {l
p
f
})) ∪ Inv
q
, T
L
= (T
p
L
↾ (L
p
\
{l
p
f
})) ∪ T
q
L
.
If the extended automaton A
p
s
has no final location,
T (p; q) = A
p
s
.
Alternative composition
Alternative composition operator p [] q models a
non-deterministic choice between p and q for action
transitions. The passage of time by itself cannot result
in making a choice. The alternative composition p [] q
is translated by merging the initial and final locations
of the extended automata A
p
s
and A
q
s
in the following
way.
T (p [] q) =
h L
p
∪ L
′
, l
p
0
, E, V
p
∪ V
q
, V
hp
∪ V
hq
, C
p
∪ C
q
, Init
p
∪ Init
q
, Inv, T
L
, l
f
i,
where if l
p
f
6= ⊤ and l
q
f
6= ⊤, then L
′
= L
q
\ {l
q
0
, l
q
f
},
E = E
p
∪ σ(σ(E
q
, l
q
0
, l
p
0
), l
q
f
, l
p
f
), and l
f
= l
p
f
.
If l
p
f
= ⊤ or l
q
f
= ⊤, then L
′
= L
q
\ {l
q
0
}, E = E
p
∪
σ(E
q
, l
q
0
, l
p
0
), and if l
p
f
6= ⊤ then l
f
= l
p
f
, otherwise
l
f
= l
q
f
.
The function Inv is defined as follows: Inv(l
p
0
) =
Inv
p
(l
p
0
) ∧ Inv
q
(l
q
0
), and Inv ↾ ((L
p
∪ L
′
) \ {l
p
0
}) =
(Inv
p
↾ (L
p
\ {l
p
0
})) ∪ (Inv
q
↾ L
′
).
Finally, if T
p
L
(l
p
0
) = u, then T
L
(l
p
0
) = u, otherwise
T
L
(l
p
0
) = T
q
L
(l
q
0
). Furthermore, T
L
↾ ((L
p
∪ L
′
) =
(T
p
L
↾ (L
p
\ {l
p
0
})) ∪ (T
q
L
↾ L
′
).
5 EXAMPLE OF THE
TRANSLATION
As an example we consider the translation of a part
of a turntable system. The turntable system illus-
trates a part of real-life manufacturing system belong-
ing to the application domain of (real-time) control re-
search (Bos and Kleijn, 2001; Bos and Kleijn, 2002;
Hofkamp and van Rooy, 2003).
The turntable system consists of a round turntable,
a clamp, a drill and a testing device. The turntable
transports products to the drill and the testing device.
The drill drills holes in the products. After drilling a
hole, the products are delivered to the tester, where the
depth of the hole is measured, since it is possible that
drilling went wrong. To control the turntable system,
sensors and actuators are used. A sensor detects a
physical phenomenon, and changes its state. The con-
troller reads the state of the sensor, and sends output
to actuators. The actuators translate output from the
controller to a physical change in the machine. Here,
the translation of the process Tester is shown.
The tester is controlled by one actuator a
1
that is
used to start or stop testing. It also has two sensors
(s
1
, s
2
). The sensor s
1
detects whether the tester is in
its initial (up) position. The sensor s
2
is used to de-
tect a test result of a product. When the tester gets the
signal to start testing it moves down. If the drilling
was successful then the tester reaches the sensor s
2
ICINCO 2005 - ROBOTICS AND AUTOMATION
490

within 2 time units. If the tester does not reach the
sensor s
2
within 2 time units, then a hole in a prod-
uct is not deep enough and a product must be drilled
again. In the χ process Tester, possible test results
are implemented by non-deterministic choice, where
the skip process term models failure. The actuator
a
1
and sensors s
1
, s
2
are implemented as the chan-
nels cTesterUpDown, cTesterUpDone, cTesterDown-
Done, respectively. When the test result of a prod-
uct is good, the process Tester sends a signal via
the channel cTesterDownDone. Otherwise, it exe-
cutes an internal action (skip). After this, the process
waits for the command to move up to the initial posi-
tion (cTesterUpDown) and then sends a signal via the
channel cTesterUpDone.
Tester( chan cTesterUpDown , cTesterUpDone
, cTesterDownDone
)=
|[ ∗( [cTesterUpDown ??]
; ∆2.0
; (cTesterDownDone !! [] skip)
; [cTesterUpDown ??]
; ∆2.0
; [cTesterUpDone !!]
)
]|
The result of applying the given translation scheme
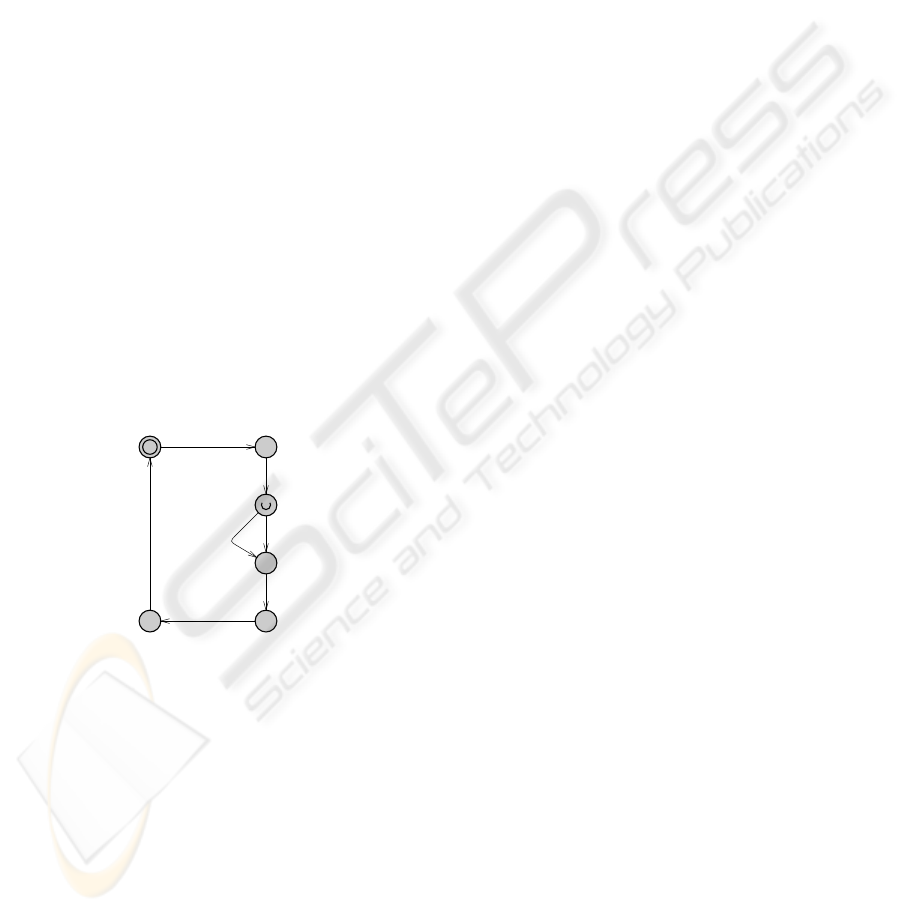
to the χ process Tester is illustrated in Figure 1.
c<=2
c<=2
cTesterUpDown?
c:=0
c==2
cTesterDownDone!
cTesterUpDown?
c:=0
c==2
cTesterUpdDownDone!
Figure 1: The Tester process translation.
After translating the χ model of the complete
turntable system to UPPAAL it becomes possible to
verify properties such as:
• The absence of deadlock.
• The turntable is not rotating if any of operations
(drilling, testing, adding or removing) is being per-
formed.
• The test result of a product will be known not later
than 31 seconds after the product has been added.
More about using UPPAAL for the verification of the
turntable model written in χ can be found in (Bortnik
et al., 2005).
6 CONCLUSIONS
Nowadays, system specification and modeling be-
come more and more important for handling increas-
ing system complexity. Satisfying industry demands
on reducing the development time (time-to-market),
costs, and increasing reliability of systems requires
early detection of the design errors, which reduces
the amount of re-work. One of the most popular
techniques to make performance analysis is simula-
tion. The process algebraic language χ has been used
extensively to model and simulate the manufactur-
ing systems. However, simulation-based performance
analysis becomes insufficient since it cannot guaran-
tee the correctness of the system. In order to check
correctness of the systems designed in χ we suggest
to translate χ models to UPPAAL timed automata and
verify their properties using UPPAAL model-checking
tool.
In this paper, the general translation of the subset of
χ to UPPAAL has been presented. The subset includes
following process terms: skip, multiple assignment,
communication actions send and receive, deadlock,
inconsistent process term, delay and delay enabling
operator, repetition, sequential and alternative com-
position.
The future work includes translation of the guard
operator, defining the equivalence relation between
the hybrid transition system of χ and the timed tran-
sition system of the UPPAAL timed automata, and ex-
tending the χ toolset with the translator from χ to in-
put language of UPPAAL. This will give the possibil-
ity to verify system properties such as the absence of
a deadlock, as well as other liveness and safety prop-
erties.
REFERENCES
Behrmann, G., David, A., and Larsen, K. G. (2004). A
Tutorial on UPPAAL. In Bernardo, M. and Corradini,
F., editors, Formal Methods for the Design of Real-
Time Systems: 4th International School on Formal
Methods for the Design of Computer, Communication,
and Software Systems, SFM-RT 2004, number 3185 in
LNCS, pages 200–236. Springer-Verlag.
Bengtsson, J. and Yi, W. (2004). Timed Automata: Seman-
tics, Algorithms and Tools. In Reisig, W. and Rozen-
berg, G., editors, Lecture Notes on Concurrency and
Petri Nets, number 3098 in LNCS. Springer-Verlag.
Bohnenkamp, H., Hermanns, H., Katoen, J.-P., and Klaren,
R. (2003). The Modest Modeling Tool and Its Im-
plementation. In Lecture Notes in Computer Science,
volume 2794, pages 116 – 133. Springer-Verlag.
Bortnik, E., Tr
ˇ
cka, N., Wijs, A., Luttik, B., van de Mortel-
Fronczak, J., Baeten, J., Fokkink, W., and Rooda, J.
(2005). Analyzing a χ model of a turntable system
VERIFICATION OF TIMED CHI MODELS USING UPPAAL
491

using Spin, CADP and Uppaal. To appear in Journal
of Logic and Algebraic Programming.
Bos, V. and Kleijn, J. (2001). Automatic Verification of a
Manufacturing System. Robotics and Computer Inte-
grated Manufacturing, 17:185–198.
Bos, V. and Kleijn, J. (2002). Formal Specification and
Analysis of Industrial Systems. PhD thesis, Eindhoven
University of Technology.
D’Argenio, P. R., Hermanns, H., Katoen, J.-P., and Klaren,
R. (2001). MoDeST - A Modelling and Description
Language for Stochastic Timed Systems. In PAPM-
PROBMIV ’01: Proceedings of the Joint International
Workshop on Process Algebra and Probabilistic Meth-
ods, Performance Modeling and Verification, pages
87–104. Springer-Verlag.
Daws, C., Olivero, A., and Yovine, S. (1995). Verifying ET-
LOTOS programmes with KRONOS. In Proceedings
of the 7th IFIP WG6.1 International Conference on
Formal Description Techniques VII, pages 227–242,
London, UK, UK. Chapman & Hall, Ltd.
Hofkamp, A. and van Rooy, H. (2003). Embedded Systems
Laboratory Exercises Manual. Eindhoven University
of Technology, Department of Mechanical Engineer-
ing.
Larsen, K., Pettersson, P., and Yi, W. (1997). UPPAAL in a
Nutshell. Int. Journal on Software Tools for Technol-
ogy Transfer, 1(1-2):134–152.
M
¨
oller, M. (2002). Structure and Hierarchy in Real-Time
Systems. PhD thesis, University of Aarhus.
Nicollin, X., Sifakis, J., and Yovine, S. (1992). Com-
piling Real-Time Specifications into Extended Au-
tomata. IEEE Trans. Softw. Eng., 18(9):794–804.
van Beek, D., Man, K., Reniers, M., Rooda, J., and Schif-
felers, R. (2004). Syntax and Consistent Equation Se-
mantics of Hybrid Chi. Technical Report 04-37, Eind-
hoven University of Technology, Department of Com-
puter Science.
van Beek, D., Man, K., Reniers, M., Rooda, J., and Schif-
felers, R. (2005). Syntax and Semantics of Timed
Chi. Technical Report 05-09, Eindhoven University
of Technology, Department of Computer Science.
van Beek, D., van der Ham, A., and Rooda, J. (2002).
Modelling and Control of Process Industry Batch Pro-
duction Systems. In 15th Triennial World Congress
of the International Federation of Automatic Control,
Barcelona, Spain, CD-ROM.
Yi, W., Pettersson, P., and Daniels, M. (1994). Auto-
matic Verification of Real-Time Communicating Sys-
tems By Constraint-Solving. In Hogrefe, D. and Leue,
S., editors, Proc. of the 7th Int. Conf. on Formal De-
scription Techniques, pages 223–238. North–Holland.
ICINCO 2005 - ROBOTICS AND AUTOMATION
492