Fuzzy Controller for Flatness Based on Neural

Network Pattern-recognition

Jian-chang Liu and Zhu Wang

(School of Information Science and Endineering, Northeastern University, Shenyang

110004, China. Correspondent: Liu Jianchang,

Abstract: A pattern-recognition method for flatness defect based on CMAC

neural network is proposed, and a flatness fuzzy controller based on the

pat-

tern-recognition

results is designed in this paper. Pattern-recognition and con-

troller are designed into a single unit, in which CMAC recognizes the member-

ship grade relative to six basic modes of common flatness defect and realizes

the seeking function of the membership grade as the forepiece of the fuzzy con-

troller for flatness directly. Through analyzing the characteristics of the flatness

defect, the fuzzy set is defined reasonably, which has greatly reduced the calcu-

lation amount of fuzzy reasoning. The result of simulation shows that the pat-

tern -recognition method of flatness offers high recognizing precision, the de-

signed fuzzy controller for flatness can control the flatness defect to expected

goal fleetly and the performance of flatness control is fine

1 Introduction

Flatness control system is a multivariable, strong-coupling, and nonlinear control

system, for which the traditional control algorithm cannot meet the ends

[1]

. For artifi-

cial intelligence technology can deal with nonlinear and indeterminacy problems, it

has become more and more popular in practice with the development of the knowl-

edge processing technology. Recently, the artificial intelligence technology has made

good winning in the application of the flatness control [2-5].

Nowadays, Neural Network(NN) is tried in the flatness pattern recognition, which

takes the flatness defect of the measurement section along the strip width as the input

of NN and the basic pattern membership grade of the flatness defect as the output.

The input of this method is so many and the structure of the network is so complex,

that the amount of NN learning work is increased, in addition the strips with different

width need different topological structures of network, as a result the method does not

have good versatility and practicability [6,7].

A pattern-recognition controller based on CMAC neural network is proposed in this

paper. Introducing actual flatness defect and six basic mode of common flatness de-

fect, Euclidean distance of which is used to express what need to be recognized in

which CMAC recognizes the membership grades relative to six basic mode of com-

mon flatness defect and realizes the seeking function of membership grade as the

forepiece of fuzzy controller for flatness directly. The result of simulation shows that

Liu J. and Wang Z. (2005).

Fuzzy Controller for Flatness Based on Neural Network Pattern-recognition.

In Proceedings of the 1st International Workshop on Artiﬁcial Neural Networks and Intelligent Information Processing, pages 42-51

DOI: 10.5220/0001191600420051

 SciTePress

the pattern-recognition method of flatness offers high recognizing precision, the de-

signed fuzzy controller for flatness can control the flatness defect to expected goal

fleetly and the performance of flatness control is fine.

2 A Pattern-recognition Based on CMAC Neural Network

2.1 Method of Flatness Pattern-recognition

During the strip production, there are many factors acting on flatness so that the flat-

ness pattern-recognition is of great importance in flatness control. No other than rec-

ognizing all kinds of characteristic information, could we have bases to determine the

flatness control strategy; otherwise all the things would be mixed together, what is

worse, the actuator would operate by mistake, sequentially, the quality of flatness

would be affected.

Task of flatness pattern-recognition is, through recognized flatness defect that flatness

meter measured

∆ (1,2im= " , m is the number of measuring section), to distin-

guish with the mode of the strip common flatness defect and help controller make

sure flatness control strategy. The paper defined six basic mode of common flatness

defect as basic mode, according to flatness control function of the mill, technology

and control requires. The result of flatness pattern-recognition is the membership

grade that discrete flatness defect

∆

is contrast to different basic mode of common

flatness defect.

During strip production, flatness measuring meter gets the distribution of strip tension

that is in the direction of transverse

T ,and the object of flatness pattern-recognition is

flatness defect

∆

.Essence of flatness defect is that distribution of strip tension in the

direction of transverse is disproportion, therefore

∆

can be expressed as:

σσσ

−=∆ ,

(1)

−=

(2)

where

— goal flatness;

— actual flatness expressed by tension difference;

T —actual tension of No.i measuring section, mi ",2,1

;

—actual average ten-

sion.

The paper defined six basic mode of common flatness defect, such as left wave, right

wave, central wave, bilateral wave, quartered wave, and anti-quartered wave.

The basic mode curves of common flatness defect are defined as Legendre polyno-

mial, which is defined as the integral of flatness defect is 0 in the direction of strip

width and six basic modes of common flatness defect are orthogonal intersection.

Particularity of flatness pattern-recognition has the requirements, such as:

(1) The total monoid of flatness pattern-recognition, such as the number of standard

sample N and the basic mode that is expressed by standard sample, is determi-

nate. The classification of mode that has a tutor should be estimated

(2) The flatness pattern-recognition is on-line running, so the operating speed must

be millisecond degree in order to satisfy the requirement of real-time control.

The conventional flatness signal process method is least-squares procedure. This

method has the defects that could not determine the degree of approximation, the

accuracy of approximation is limited and the physical conception of regression coef-

ficient is indefinite in order not to express the value of actual flatness defect defi-

nitely. It could not satisfy the requirements of flatness control, which demands high

accuracy and complicated control strategy. Therefore, it is necessary to find new

method.

2.2 Model Design of CMAC Flatness Pattern-recognition

The basic thinking of CMAC NN is to learn eigen approximate value of system. Then

it generates right control signal. The eigen approximate value of system is based on

learning of the result that input and output data are gradually observed. Therefore,

CMAC NN is more suitable for flatness pattern-recognition.

(1) Design of input parameter

The paper uses the Euclidean distance [8] to express the flatness to be identified.

Namely takes the Euclidean distance between the actual flatness sample and the six

basic mode of common flatness defect as the input of the network. It simplifies the

structure of the network and ensures the effectivity of network-topological when the

width of the strip changes.

Suppose that the actual detected sample to be identified was normalized

()

)(),2(),1( mY

"= ,6 standard samples were normalized as

()

)(),2(),1( mY

kkkk

"= ( 62,1 "

k ), then the Euclidean distance between the

sample Y to be identified and k standard sample Y

is as follows:

()

∑

−=−=

kkk

iiYYD

)()(

σσ

(3)

Normalized as:

∑

; k=1,2…6 .

(4)

Take

DD as the input of CMAC network, then recognize the pattern by network

learning.

(2) Design of output parameter

The six basic modes of common flatness defect included 3 pairs of reciprocal relation

mode, such as left wave and right wave, central wave and bilateral wave, quartered

wave and reverse quartered wave. According to the actual flatness during operation

of rolling, the reciprocal relation modes of the six basic modes of common flatness

defect could not exist at the same time. Therefore the output layer of CMAC NN has

three output points, which can correctly express the membership grade of each basic

mode.

Suppose the output of 3 pairs of reciprocal relation mode in responding to CMAC

NN is

and

respectively, and when

and

is positive, it represents left

wave, central wave and quartered wave respectively; when

and

is negative,

it represents right wave, bilateral wave and reverse quartered wave respectively.

(3) The procedure of CMAC flatness pattern-recognition

1) Measure the distributed value of strip tension T

(i=1,2…m);

2) Calculate actual remainder tension

−=

;

3) Calculate value flatness defect

σσσ

−=∆ , calculate maximum value flatness

defect

∆max ;

4) Normalize flatness error:

∆

=∆

max

;

5) Calculate the normalized Euclidean distance DD

(k=1,2…6) between

∆ and

basic flatness modeY

, take it as the input of the CMAC NN;

Obtain the corresponding normalized network output:

and

3 Fuzzy Controller Based on the Flatness Defect Pattern-

Recognition

In this paper, six-roll cold rolling mills was studied. Flatness control method included

work roll bender, intermediate roll bender and support roll screw down levelling.

Different flatness control method was used to eliminate different flatness defect, such

as intermediate roll bender was used to eliminate central wave, work roll bender was

used to eliminate positive quartered wave and negative quartered wave, support roll

screw down levelling was used to eliminate side wave, and so on. To eliminate the

un-disciplinarian remainder flatness defect, spot coolant jetting was used, which is

not included in this paper.

The structure diagram of fuzzy controller based on the flatness defect pattern recogni-

tion results is shown in Fig. 1.

Where, F

, and F

——the controlled variables of work-roll bender, intermediate

roll bender and support roll screw down levelling respectively; T

(i=1,2…m)——the

actual tensile stress for the measuring section i.

The membership grade of the actual flatness defect relative to the six flatness defect

basic patterns can be used as fuzzy controller foreside to solute membership grade by

membership function. Actuater control value can be obtained through fuzzy reasoning

and fuzzy solution from recognition results.

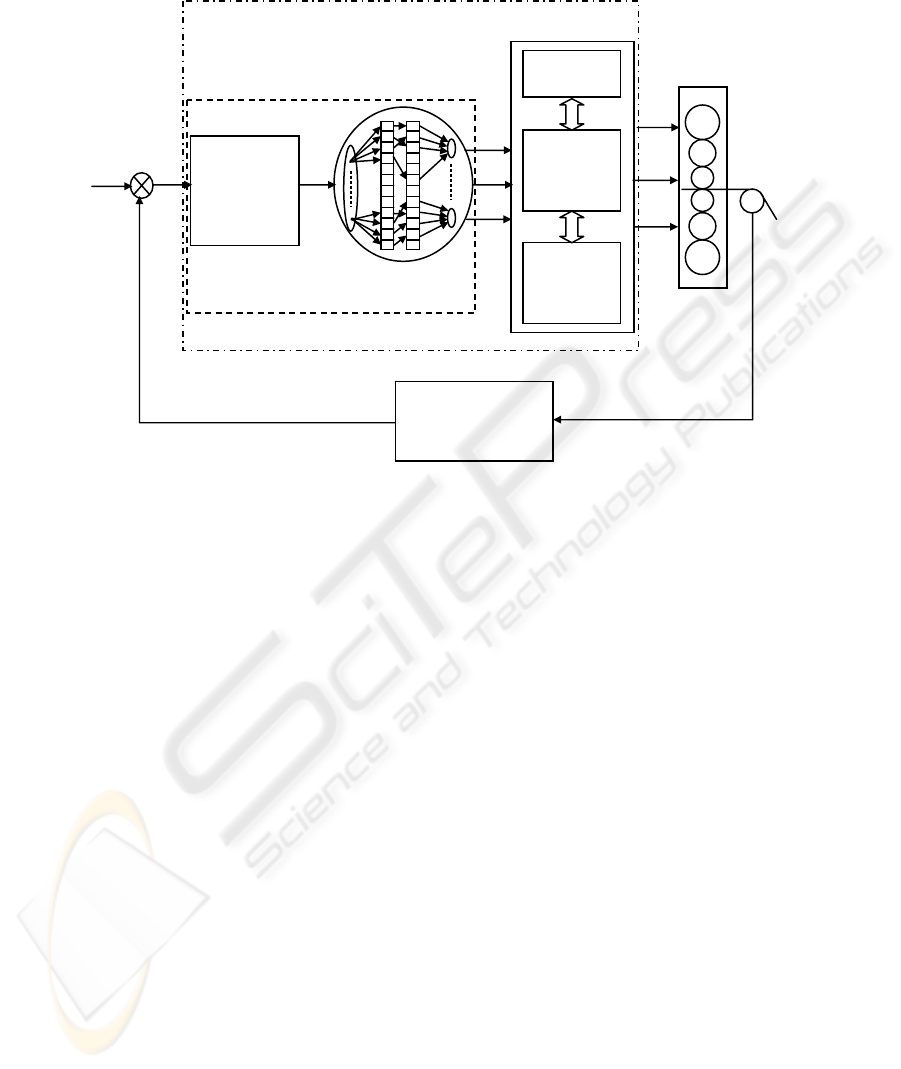
There are three flatness defect model membership grades of CMAC network output,

which express six flatness pattern membership grade because of the existence of the

positive and negative, so there must be three zeros. It needs to have many parameters

of fuzzy control such as input variable, fuzzy set of input variable, membership func-

tion, output variable and fuzzy set of output variable and so on, the membership func-

tion has been realized by neural network, so the others need to be defined.

The goal of fuzzy control is to eliminate flatness defect, so the flatness defect

∆ can

be defined as input variable, six flatness defect basic modes can be defined as six

fuzzy sets, actuater control variable as output variable, in the same way, output vari-

able includes six fuzzy sets. It needs to be noticed that the fuzzy sets relative to the

different control method are different.

Intermediate roll bender is more useful to eliminate double side wave and central

wave, less useful to eliminate positive quartered wave and negative quartered wave,

and almost useless to eliminate single side wave. Five fuzzy sets are defined, double

side wave is PB(positive big),central wave is NB(negative big),negative quartered

wave is PS(positive small ),positive quartered wave is NS(negative small), left side

wave and right side wave are ZE(zero).There is something to be noticed that left side

wave and right side wave are combined as one fuzzy set ZE. In the same way, there

are five fuzzy sets of control variable .The fuzzy reasoning rules are as follows:

is NB, then

F is NB;

is NS, then

F is NS;

is ZE, then

F is ZE;

∑

Euclidean

distance

computing

repositor

fuzzy-

deducing

defuzzi-

fication

actual flatness

computing

CMAC NN

flatness pattern recognition

control deducing

flatness fuzzy controller

∆

flatness

roll

rolling

mill

Fig. 1. Flatness fuzzy controller based on CMAC pattern recognition

is PS, then

F is PS;

is PB, then

F is PB.

The result of neural network recognition is [

321

], if 0

,then

is the

membership grade of PB, the membership grade of NB is zero; if

,then

the membership grade of NB, the membership grade of PB is zero. Similarly, we can

get the membership grade of PS and NS based on

.Because left side wave and right

side wave are the same fuzzy set ZE, so the membership grade of ZE is

After the fuzzy sets and corresponding fuzzy reasoning rules are defined, fuzzy rea-

soning can be done. In the paper, control variable

′

can be obtained through de-

fuzzification using weighting average method, then multiplied by

∆max

, in this

way, the actual change value

F of intermediate roll bender can be got. 0>

F , denote

that positive bender control value is

F ; 0

F ,denote that negative bender control

value is

F .

To work roll bender, negative quartered wave is defined as PB(positive big),positive

quartered wave is NB(negative big), double sides wave is PS(positive small), central

wave is NS(negative small),left side wave and right side wave is ZE(zero).The rea-

soning process of it is the same as intermediate roll bender.

For the particularity of fuzzy set and membership function definition, actuater control

variable can be obtained through weighting average defuzzification method:

(1) weighting average method

If the membership function of every fuzzy set of language variable Z is defined as

single point, then the fuzzy rules are:

: if x=A

and y=B

,then z=z

among which

()

niz

",2,1= is the real number value in domainZ[-1,1],if the mem-

bership grade of rule is

,then the result

z is:

∑

(5)

(2) Defuzzification method

Based on the particularity of the arithmetic in the paper, the output variable fuzzy sets

are defined as fuzzy single point function in domain

]1,1[

−

, the corresponding relation

are shown in table 1.

Therefore, different flatness defect corresponds to different membership grade com-

pounding, then the corresponding actuater control variable can be obtained based on

fuzzy rules and defuzzification method.

Table 1. Corresponding value of fuzzy set and single point

Fuzzy set NB NS ZE PS PB

Fuzzy single point

value

-1 -0.5 0 0.5 1

Table 2. Relationship between fuzzy set and membership of IR bender

Fuzzy set NB

ZE PS PB

Grade of member-

ship

0.301

0.296

0.402

Table 3. Relationship between fuzzy set and membership of WR bender

Fuzzy set NB NS ZE PS PB

Grade of member-

ship

0.301

0.296

0.402

For example, the maximum of real flatness defect is

I15max =∆

at some time, the

output of CMAC neural network is [0.2961 -0.3015 0.4024], then the membership

grade denoting real flatness defect to left side wave is 0.2961, double sides wave is

0.3015and positive quartered wave is 0.4024,which is obtained through membership

grade linear combination of the three flatness basic modes. To work roll bender and

intermediate roll bender control, the relationship between flatness defect fuzzy set and

membership grade is shown in table 2 and table 3.

After the contribution of every rule is obtained, the next step is to get the output ac-

cording to fuzzy reasoning rules, that is to determinate the precise value of work roll

bender and intermediate roll bender control values respectively. The gravity model

approach method is used in the process, the results are as follows:

5045.115

04024.02961.003015.0

014024.05.02961.0005.03015.01

−=×

++++

×+×+×+×−×−

(kN)

7748.315

4024.002961.03015.00

4024.0105.02961.003015.05.001

=×

++++

×+×+×+×−×−

(kN)

4 Simulation Test

4.1 Simulation of Flatness Defect Pattern-recognition

Simulation-test using the CMAC model , is related in part two, simulation parameter

contains: the quantified degree of CMAC pattern-parameter R=20, receptive field

5C = ,study coefficient

7.0=

,physics memory space 4096

A , the member of

training sample

100=n ,the expected goal function

∑

−

10 ,the max step of

training 3000=S .

There is always some relict flatness defect in reality. In this case, whether the base

model flatness defect can be recognized exactly has become one of the standards,

which can judge the pattern-recognition method for flatness defect based on CMAC.

Here, the irregular disturbance Y

that is produced by random function is used to

simulate the relict flatness defect, which can be combined to flatness defect of basic

mode, and then be sent to CMAC recognition model. The results are shown in table 4.

Table 4. Recognizing result of flatness

Testing sample Expected output actual output

YYY=+

1, 0,

µµ

0.9853, 0.0130,

0.0072

µµ

==−

147

0.4 0.6YYYY=++

0.4, 0.6,

µµ

==−

0.3956, 0.6143,

0.0225

µµ

==−

257

0.7 0.3YYYY=++

0.7, 0,

0.3

µµ

=− =

0.7109, 0.0103,

0.2963

µµ

=− =−

367

0.1 0.9YY YY=++

0, 0.1,

0.9

µµ

=−

0.0032, 0.1107,

0.8982

µµ

=− =

=−

The result of simulation shows that the recognized precision of CMAC NN model is

higher, the capability of anti-interference is stronger. So it is an effective and feasible

method of intelligent recognition.

4.2 Simulation Test of Flatness Fuzzy Control

The flatness defect can be divided into two parts: symmetry and asymmetry. Take the

symmetry part as an example. The formula is as follow:

(

)

xxxy

λλ

+= .

(

The flatness defect of thesymmetry part can be eliminated by work roll bender and

intermediate roll bender.

From the Fig.1, it can be seen that the maximum value of symmetry flatness defect

lies in the

1±

and

of strip regular width. Briefly, introduce symmetry flatness

parameter

A and

A to express the flatness defect. Define

A and

A as:

(

)

4212

λλ

+=±= yA ,

(

4214

λλ

⎟

⎠

⎞

⎜

⎝

⎛

±= yA .

(

The procedures of simulation are as follows:

(1)

Get the expression of symmetry flatness defect through the flatness defect

∆ to

be identified, then calculate

A and

A ;

(2)

Send input

∆ to CMAC pattern-recognition network, then output is the mem-

bership grade of basic mode. After that, send the membership grade to flatness

fuzzy control algorithm, then the outputs are the control variables of work roll

bender and intermediate roll bender:

F and

F ;

(3)

The actuater eliminates the flatness defect according to

F ,

F and unit control

variable. Briefly, the effectiveness of unit control variable of the two benders can

be expressed by approximate linear model.

(4)

The remainder flatness defect is reverted to the flatness defect expression and

when

A and

A reach the expected goal, simulation is over. Otherwise it returns

to procedure 1 to continue next control period.

When

I3125.19

−=A , I2969.11

−=A , the actual flatness defect is center wave, the

terminating condition of simulation is that

A and

A are all less than I2

,the result

are in Fig.2.

When

I6875.10

=A , I4219.9

−=A , the actual flatness defect is quartered wave, the

terminating condition of simulation is that

A and

A are all less than I2

,the result

are in Fig.3.

-1 -0.5 0 0.5 1

-20

-10

-1 -0.5 0 0.5 1

-20

-10

where,

a is the curve of the actual flatness error, b is the curve of the final flatness

error disposed by fuzzy control. It can be seen that the maximum value of flatness

error in Fig.2 can reach the range of ±0.4I after 3 control periods; the maximum value

of flatness error in Fig.3can reach the range of ±1.6I.

The result of simulation shows that the designed fuzzy controller for flatness ex-

pressed in Fig.1 can control the flatness defect to expected goal fleetly, the precision

of flatness control can reach to ±2I and the performance of flatness control is fine.

flatness defect (I)

Fig. 2. Simulation results of central wave

Fig. 3.

Simulation results of quartered wave

normalized stri

width

normalized stri

width

5 Conclusion

A pattern-recognition method for flatness defect based on CMAC neural network is

proposed, and a flatness fuzzy controller based on it is designed in this paper.

Through the analysis of flatness defect characteristic, the fuzzy set is defined ration-

ally, which have reduced the calculation amount of fuzzy reasoning greatly. Pattern-

recognition and controller are designed to be combined into a single unit, in which

realize the seeking function of membership graded as the fore piece of fuzzy control-

ler for flatness directly. At the same time, rationally design the fuzzy controller. The

result of simulation shows that the pattern -recognition method of flatness offers high

recognizing precision, the designed fuzzy controller for flatness can control the flat-

ness defect to expected goal fleetly, the precision of flatness control can reach to ±2I

and the performance of flatness control is fine.

References

1. Burnham, Cole R, Gentile I, Neville A. Model based flatness control of thin strip and foil[J],

Iron and Steel, 2003,38(6):36-40

2. Wang GD, Liu XH. The Artificial Intelligent Optimization in Rolling Process of Metal[M],

Beijing: Metallurgical Industry Press,2000.3:2-18

3. Wang FH, SUN YK, Wang XP. Application of Fuzzy Neural Network Based on Immune

Algorithm( IA) to AGC2ASC System[J], Information and Control, 2004, 33(4): 504-507

4. Zhu HT, Jiang ZY, Tieu AK, Wang GD. A fuzzy algorithm for flatness control in hot strip

mill[J] , Journal of Materials Processing Technology 2003, 140 (3): 123–128

5. Wang FH, Sun YK, Chen ZY. Strip flatness and gauge composite control system based on

fuzzy neural networks[J]. Journal of University of Science and Technology,

2003,25(2):182-184

6. Jelali M, Muller U, Wolff A, Ungerer W, Thiemann G. Advanced measurement and flatness

control for hot strip mills[J]. Cahiers D'Informations Techniques, 2002,99(6):517-522

7. Peng Y, Liu HM, Pattern Recognition Method Progress of Measured Signals of Shape in

Cold Rolling[J]. Journal of Yanshan University, 2003, 27(2): 142-145

8. Aleksander K. Basic function model of the CMAC network[J].Neural Network,2000,12:107-

126