Characterising Evoked Potential Signals Using Wavelet

Transform Singularity Detection

Conor McCooey

and Dinesh Kant Kumar

School of Electrical & Computer Engineering, RMIT University, PO Box 2476V,

Melbourne,VIC 3000, Australia

Abstract: A new method of viewing evoked potential data is described. This

method, called the peak detection method, is based on singularity detection

using the discrete wavelet transform. The peaks and troughs of an EEG

recording are identified and characterized using the algorithms of this method,

resulting in a linear decomposition of the data into sets of individual peaks.

Then, by classifying the peaks in terms of latency (time), magnitude (voltage

potential) and width (scale), the locations of higher concentrations of similar

peaks are identified. These are grouped and sub-averaged, yielding sets of sub-

averaged peaks that characterize the shape and give a measure of the

repeatability of particular sub-averages within the visual evoked potential

ensemble average signal. This method highlights evoked potential features that

may be obscured or cancelled out with standard ensemble averaging. This is

demonstrated for visual evoked potential data taken from a single subject.

1 Introduction

Electroencephalography (EEG) is the electrical recording of brain activity and is

generated by the summation of spatially and temporally separated action potentials. It

is a complex signal and even though it appears noisy, is very useful for identifying

certain brain conditions. For many years the frequency spectrum of EEG has been

examined and usefully interpreted for clinical and research purposes.

The Fourier transform uses time invariant sine waves and effectively gives a

measure of the presence of a particular range of frequencies of a given time course

signal. In the process of performing the transform the time location of the frequency

is lost. The wavelet transform [1] uses time bound waves (wavelets) and may be

thought of as an extension of the Fourier transform where the frequency content and

time location are recorded simultaneously. Wavelet representations are more efficient

than the traditional Fourier representation where the signal is non-stationary such as

EEG. Such a method is able to localize the time when changes in the signal properties

occur.

Evoked Potentials (EPs) are EEG recordings in response to visual, auditory or

somatosensory sensory stimulation. EPs are used by clinicians to study specific

neurological disorders. Due to the presence of background activity and noise, a single

stimulus response is not detectable because the signal of interest is embedded in

similar-sized or larger ongoing background EEG signals and so multiple stimuli

McCooey C. and Kant Kumar D. (2005).

Characterising Evoked Potential Signals Using Wavelet Transform Singularity Detection.

In Proceedings of the 1st International Workshop on Biosignal Processing and Classiﬁcation, pages 3-11

DOI: 10.5220/0001191700030011

 SciTePress

triggered recordings are taken. Typically, ensemble averaging is used to detect the

Evoked Potential and in the case of visual evoked potentials (VEP) requires 100 to

200 repeats of the stimulus to obtain an observable response. Averaging of these

epochs reduces the uncorrelated background EEG signals which tends towards a zero

level as it is considered random in nature, while the stimulus response is time-locked

to the stimulus and so averages to a particular voltage profile.

If the EP recording consisted purely of the time-locked stimulus response and the

background activity was purely Gaussian in nature, then there would exist a high

degree of repeatability across sequential tests on individual subjects. Experience

under such conditions shows that, while strong similarities show through the EP,

significant variations from one test to the next are observed.

Obtaining single-trial evoked potential reconstruction would greatly assist in

addressing some of the unanswered questions regarding evoked potential activity.

Researchers have attempted to develop several methods to discern the sought-after

signal from the background activity. These include time-frequency digital filtering

[2], Matched Filtering [3], Wavelet Denoising [4] and Wavelet Thresholding.

One important property of EEG recordings is the presence of singularities and

peaks. EEG signals are characterized by sharp, irregular non-stationary transitions,

which are known as singularities [5]. The singularities of EEG have been investigated

using a different method called fragmentary decomposition [6] with the same goal of

eliciting a better understanding of the EEG recording using discrete peaks.

This research aims to determine the singularity features of EEG recordings in order

to overcome some of the limitations in the analysis of evoked potentials by averaging.

This paper describes a method where the singularities are grouped together to identify

the individual peaks that are the basic building block of the EEG recordings.

2 Theory

A wavelet is a time domain wave which is localized, oscillatory and with zero

average. A wavelet, ψ(t) may be expressed in terms of a scale or dilation factor, s,

which as it is varies compresses or expands the wavelet shape and a translation factor,

u that shifts the wavelet along the time axis. Wavelets have narrow time and

frequency support (ideally) and are suitable for singularity identification and peak

detection.

The output of the wavelet transform is a set of coefficients along the time axis for

each scale factor [7]. These coefficients indicate the correlation between the signal

and the wavelet at the specific scale and translation. These are larger when the signal

at the temporal location of the wavelet has spectral properties similar to the wavelet

scale.

One practical implementation of the dyadic wavelet transform uses a filter bank

algorithm and a dyadic scale (2

) and is called the “algorithme à trous” [5]. It

generates a detail component (similar to a low pass filter) at each 2

scale up to the

maximum calculated scale, together with a remaining approximation component. By

selecting the wavelet function to be the derivative of a smoothing function, such as

the quadratic spline wavelet of degree 2, the evolution of the local maxima of the

wavelet transform modulus across scales can be used to detect local singularities. The

detail components, taken from the “algorithme à trous” method, yield a set of

coefficients for each scale.

By selecting only the modulus maxima values that fitted a linear relationship

across scales, a large set of wavelet coefficients may be simplified into a much

smaller discrete set of coefficients grouped per singularity [5]. This is a powerful step

forward in the characterization of a signal into a group of singularities. An inverse

discrete wavelet transform algorithm that gives a good estimate of the original signal

has also been demonstrated [5].

The technique reported in this paper detects singularities using the Discrete

Wavelet Transform (DWT). Singularities are grouped into peaks within the signal and

the EEG recording is decomposed into a linearly independent set of peaks that sum to

approximate the original signal.

Once identified, each peak is then described by its characterizing features - time

latency, width of peak and height of peak and then classified using these properties to

populate a multi-dimensional matrix. Performed across all peaks and all epochs for

the full EEG recording, this allows areas of local concentration to be identified. This

local activity may then be extracted and sub-averaged to yield a localized EP signal.

This paper demonstrates that the concentration matrices used in conjunction with the

ensemble averaging may be used to decompose the EP peaks.

This paper reports the use of the technique for flash visual evoked potentials

(VEP). This could be extended to other stimulation techniques. Other possible

applications include denoising, data compression and all applications where non-

stationary signal activity is important.

3 Method

3.1 Peak Detection

Singularity detection using the DWT [5] is the starting point for the theory outlined in

this paper. Singularities characterize areas of large magnitude change in the signal

over a short period i.e. points where there is a large slope. A peak may be thought of

as a pair (or triplet) of singularities that record a simple shift away from and back to a

particular baseline. These singularity coefficient sets are matched into pairs (or

triplets) that identify distinct peaks within the data. The position and value of both the

detail and approximation components are recorded in a single line of an array for each

singularity. Using these arrays, sets of singularities are made that would combine to

make peaks using a set of guidelines listed below:

(a) A pair of singularities is more likely to form a peak if the absolute magnitudes of

the detail components at the highest scale level for each singularity are similar to one

another.

(b) Singularities that increase with time have positive coefficients and those that

decrease with time have negative coefficients. Therefore a peak must be made up of

both positive and negative coefficient singularities.

level within ±1 scale factor of each other.

(d) The gap between the position of the first detail component of each singularity in a

pair is related to the dyadic scale factor and fits the rule in equation (1) where p

)

represents the first coefficient value for singularity (g

) and x is a sequential list of

identified singularities.

< p

) – p

) < 2

s+1

. (1)

The PDM algorithm matches the singularities to generate singularity sets governed

by the above guidelines. Using the inverse DWT and only the coefficients of each

singularity set, a signal representation for each identified peak is generated. These

peaks are added together, in the time domain, to yield a close approximation of the

original signal. All peaks are defined as starting at the zero baseline, deviating either

positively or negatively and returning to the baseline. Bi-phasic peaks are divided

into 2 mono-phasic peaks – one positive and one negative. The features of all the

detected peaks are identified. The result of this is the decomposition of the original

signal into a linear set of separable peaks, which can be recombined to reconstruct the

original signal.

3.2 Classification of Peaks

To identify whether the peaks represent the signal, features of the signal, and the

peaks representing the signal, were extracted. The features of each of the peaks

detected in section 4.2 were identified based on the following:

(a) Direction of the peak (positive or negative)

(b) Latency (time between stimulus onset (zero time) and the max peak magnitude)

(d) Peak width measured from max height to 10% of max height above baseline

These criteria were calculated from the peak signals generated by the inverse

transform of the singularity coefficient sets. However, it is envisaged that in future,

these criteria will be calculated directly from the singularity coefficient sets. Next,

these criteria were used to populate two matrices, each of three dimensions,

representing the properties of the peaks. These matrices identify the region of

concentration of peaks. One matrix was for positive and the other for negative peaks,

and the dimensions of each matrix correspond to the latency, height and width

parameters. The local area within the matrix corresponding to the associated temporal

latency, height and width location was incremented by a single value 1 for each

identified peak. This was repeated for every peak of every epoch and the result was a

concentration matrix where there was a cluster around areas of higher matrix value

indicating regions where there were multiple similar type peaks.

The highest concentration region was identified and the corresponding value was

computed and thus all peaks associated with that concentration value were identified.

Local average or sub-averaging of the highest concentration region was calculated to

give the trend of the local peak shape and characteristics. After obtaining the trend, all

peaks related to this region were removed from the concentration matrices and the

process repeated for the next highest concentration region. This process was repeated

iteratively until both concentration matrices became empty.

Examination of the concentration matrix identified peaks with similar properties

and grouped them. Each group of peaks is sub-averaged to give a representative

signal for that group. To determine the quality and usefulness of the technique, sub-

averages were compared to the standard ensemble average by two visual tools.

The first measure consisted of plotting and summing all the sub-averaged peaks in

a region and comparing to the standard ensemble average signal. Peaks that appear

less often get reduced while those peaks that occur more often get relatively

amplified. This is then compared to the standard averaged signal. This gives a genuine

representation of the sub-average magnitude and shape.

For the second measure, a slightly different sub-average is measured where the

group of peaks are added and then divided by the total number of all peaks. In this

way, the contribution of each sub-average to the standard ensemble average may be

compared, as the denumerator in the averaging calculation is the same.

4 Results

Flash Visual Evoked Potential signals were taken for a single subject. Ethics approval

for the experimental procedure was obtained from the local Human Research Ethics

Committee. Repeated strobe light flashes were presented to the subject’s visual field

at a distance of about one metre from the eye at an approximate rate of 1 per second.

The response was measured Mid-Occipital (MO) location, which is located at a point

5cm directly above the inion [8]. An epoch length of 500ms was recorded

synchronously with the strobe flash. The data was normalized to give a zero mean

across all data. Visual inspection was performed to remove gross artifacts. Partial

peaks occurring at the edges of each epoch were removed to eliminate border effects

from the subsequent DWT processing. A total of 104 epochs were measured.

The Peak Detection Method was applied to each epoch to identify and characterize

the major peaks. Pearson’s correlation coefficient was calculated for each epoch

signal and its corresponding PDM signal. A correlation coefficient of 1 represents a

perfect match between signals. Three epochs had a correlation coefficient below 0.86

and these were discarded from further analysis leaving 101 epochs. The mean

correlation coefficient of these 101 epochs is 0.9560 with a standard deviation of

0.0211. This suggests that using the PDM, it was possible to approximate the original

signals well.

The comparison of the VEP signal generated using ensemble averaging and the

sub-average from all the peaks using peak detection method for all the 101 epochs is

in Fig. 1. It is observed that the PDM average gives a good approximation of the

ensemble average signal. This indicates that decomposing the evoked potential

response into a set of peaks has retained the information that is observable by

ensemble averaging.

Fig. 1. Comparison of ensemble VEP average and sum of peak detected with PDM divided by

total number of peaks

The concentration matrices were generated from all the peaks across the 101

epochs used. From these matrices the location of the highest value in either matrix

was identified. Reading the matrix parameters for this location identifies that the

highest repetition was of a negative peak located at a latency of 144.5ms, with a

height of 8µV and a width of 31.25ms. Of the 101 epochs, 31 contain a peak with

similar characteristics to this. All peaks associated with this location were then

removed from the concentration matrix and the next highest value in either matrix

was identified. This process was iterated until both matrices were empty and all

peaks were grouped. The number of peaks in each group is charted in Fig. 2. In a

purely random system, one would expect a more horizontal trend however the left

hand skewness indicates identification of areas of increased concentration of EEG

activity. The summation of all 231 sub-averages yields the same PDM average

illustrated in Fig. 1.

Fig. 2. Histogram showing the ordered sequence of sub-average peaks versus number of peaks

within each sub-average.

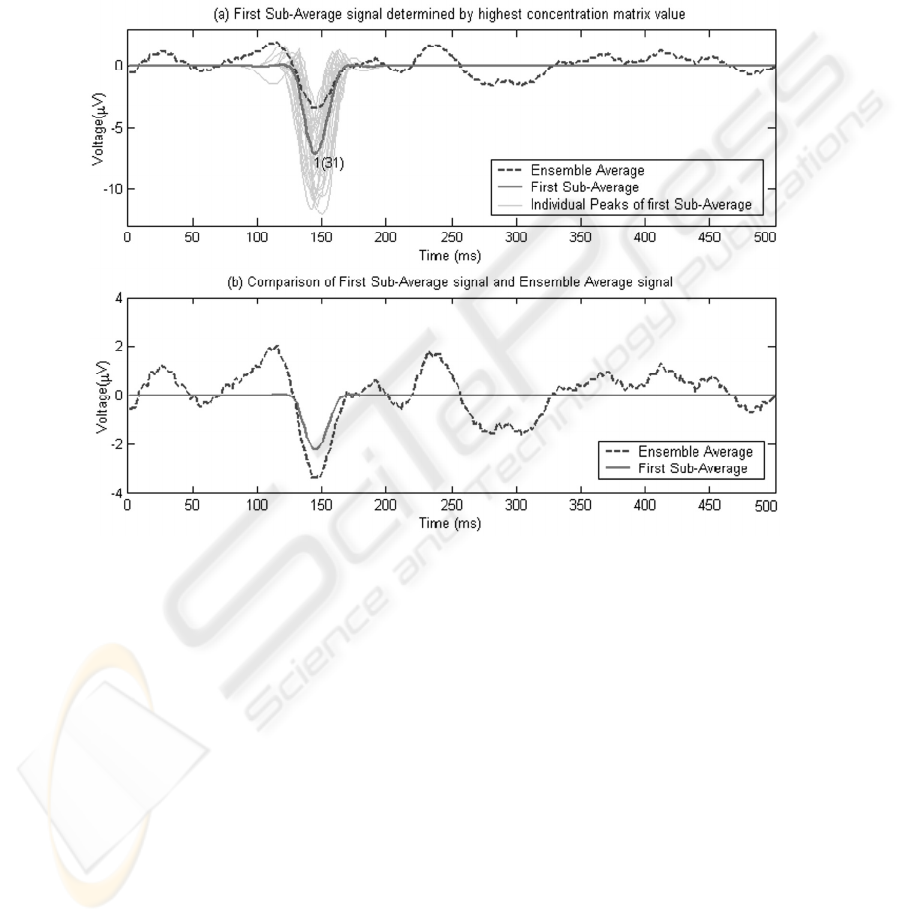
Results for the first sub-average are presented in Fig. 3. The ensemble average is

shown as a dashed line in both Fig. 3(a) and Fig. 3(b) for comparative purposes. In

Fig. 3(a), all 31 individual peaks of the first sub-average are plotted together with the

average of these 31 peaks. This is the actual average determined by summing all 31

peaks and dividing by the actual number of epochs selected, which is 31. Fig. 3(b)

illustrates the average of the 31 peaks determined by adding up all 31 peaks but

dividing by the total number of epochs which is 101 in this case.

Fig. 1. Examination of the First Sub-Average determined by the highest value in either

concentration matrix representing the similar peaks that occurs most often. In this case, there

are 31 peaks out of a possible 101 epochs.

The first sub-average in Fig. 3(b) is directly comparable with the Ensemble

Average since these are both averaged over the 101 epochs. It is a scaled version of

first sub-average in Fig. 3(a). This comparison gives a good indication of how the first

sub-average peak compares to the ensemble average peak in local area.

After calculating the first sub-average, the subsequent sub-averages were

calculated. The number of peaks identified in each sub-average group is charted in

Figure 2. It is observed that some sub-averages are more significant than others.

Based on this, a summation of the first 15 sub-averages is presented in Fig. 4. Again,

the ensemble average is shown as a dashed line in both Fig. 4(a) and Fig. 4(b) for

comparative purposes. The cumulative sub-average average by 31 epochs is shown in

Fig. 4(a) and scaled by 101 epochs in Fig. 4(b) is shown by the thick straight line.

Individual sub-averages also shown in Fig. 4(a) as a light thin line.

It is noted from Fig. 4(b) that for the most part, the fifteen chosen sub-averages

correlate with major peaks of the ensemble average. These have been identified with

a lower number of epochs ranging from 31 down to 14. However, it is important to

note that the full 101 epochs needed to be calculated in order to pick out the sub-

averages.

Fig. 2. Examination of the first 15 Sub-Average signals. Indices in (a) are annotated as x(y)

where x is the order number for the sequence of sub-averages (1-15) and y is the number of

peaks in that sub-average (when x=1, y=31).

5 Discussion

It is observed that the summation of the 15 sub-averages in Fig. 4(b) retains the major

features of the ensemble average. These 15 sub-averages represent a total of just 283

peaks used out of a total of 1278 peaks originally identified in the 100 epochs of data.

Hence only 22% of the total Evoked Potential raw data is used to generate this

averaged evoked potential. It is also observed that this cumulative sub-average tracks

the standard ensemble average well. The notable exception is the appearance of a

negative peak at 82ms, which is not apparent in the ensemble average signal. Further

scrutiny of the remaining sub-averages reveals that in the ensemble average, this

peaks is cancelled out by a positive peak at this time position which has a large

magnitude but a small number of repetitions. This represents a possible advantage of

this system over the typical ensemble average system where such a peak is not

evident and could result in loss of information.

Separating overlapping peaks is an important and difficult component of any

singularity detection technique [6]. On occasion, some detected peaks do not have a

close fit to the original. However, it is observed that the vast majority of epochs give

an excellent fit to the original signal.

A new method of peak detection for evoked potentials has been presented. Using

an example of VEP based EEG data generated using 104 experiments, this peak

detection method is shown to retain the same evoked potential information as the

ensemble averaging technique. It is envisaged that this tool could help interpret the

visual evoked potential in two ways. Firstly, the higher concentration locations

indicate a more repeatable evoked potential signal and hence give a reliability factor

to the peak that is being viewed. Secondly, when cancellation of positive and

negative peaks occurs, the make-up of that cancellation may be examined in terms of

size of peak and number of times it occurs. Further testing and analysis of this

technique is being undertaken to broaden its application and to verify the results more

generally.

References

1. Grossman, A., Morlet, J.: Decomposition of Hardy Functions into Square Integrable

Wavelets of Constant Shape. SIAM J. Math. 15 (1984) 723-736

2. Demiralp, T., Yordanova, J., Kolev, V., Ademoglu, A., Devrim, M., Samar, V. J.: Time-

Frequency Analysis of Single-Sweep Event-Related Potentials by Means of Fast Wavelet

Transform. Brain and Language 66(1) (1999) 129-145

3. Maclennan, A. R., Lovely, D. F.: Reduction of Evoked Potential Measurement by a

TMS320 Based Adaptive Matched-Filter. Medeical Engineering & Physics 17(4) (1995)

248-256.

4. Quiroga, R. Q., van Luijtelaar, E. L. J M.: Habituation and Sensitization in Rat Auditory

Evoked Potentials: a Single-Trial Analysis with Wavelet Denoising. Int. Jour. Of

Psychophysiology 43 (2001) 141-153

5. Mallat, S., Hwang W. L.: Singularity Detection and Processing with Wavelets. IEEE

Transactions on Information Theory 38(22) (1992) 617-643

6. Melkonian, D., Blumenthal, T. D., Meares, R.: High Resolution Fragmentary

Decomposition – a Model Based Method of Non-Stationary Electrophysiological Signal

Analysis. Journal of Neuroscience Methods 131 (2003) 149-159

7. Mallet, S.: A Theory for Multiresolution Signal Decomposition: the Wavelet

Representation. IEEE Trans. on Pattern Analysis and Machine Intelligence 11(7) (1989)

674-693

8. Misulis, K. E.: Spehlmann’s Evoked Potential Primer, 2nd edn, Butterworth-Heinemann

(1994)