
Evolutionary Techniques for Neural Network
Optimization
Eva Volná
University of Ostrava, 30ht dubna st. 22, 701 03 Ostrava, Czech Republic
Abstract. The idea of evolving artificial networks by evolutionary algorithms is
based on a powerful metaphor: the evolution of the human brain. The
application of evolutionary algorithms to neural network optimization is an
active field of study. The success and speed of training of neural network is
based on the initial parameter settings, such as architecture, initial weights,
learning rates, and others. A lot of research is being done on how to find the
optimal network architecture and parameter settings given the problem it has to
learn. One possible solution is use of evolutionary algorithms to neural network
optimization systems. We can distinguish two separate issues for it: on the one
hand weight training, and on the other hand architecture optimization. Next, we
will focus on the architecture optimization and especially on the comparison of
different strategies of neural network architecture encoding for the purchase of
the evolutionary algorithm.
1 Genetic background for network topology optimization
The typical network considered here is a directed acyclic graph of simple neurons or
units. Each unit has a state, represented by a real number, a set of input connections,
and a set of output connections to other units. The connections themselves have real-
valued weights, w
ij
. A unit’s state, o
i
is computed as a nonlinear function of the
weighted sum of the states of units from which it receives inputs. The nonlinear
activation function is a sigmoid, effectively endowing the unit with a threshold action;
the position of the threshold is controlled with a bias or „threshold weight“, q
i
. This is
summarized in equations:
1
1
)1(
−
−
=
+=
+=
∑
i
s
i
n
j
ijiji
eo
ows
θ
.
(1)
A subset of the units is designated as input units. These units have no input
connections from other units; their states are fixed by the problem. Another subset of
units is designated as output units; the states of these units are considered the result of
the computation. Units that are neither input nor output are known as hidden units.
Volná E. (2005).
Evolutionary Techniques for Neural Network Optimization.
In Proceedings of the 1st International Workshop on Artificial Neural Networks and Intelligent Information Processing, pages 3-11
DOI: 10.5220/0001191800030011
Copyright
c
SciTePress
A problem will specify a training set of associated pairs of vectors for the input units
and output units.
The full specification of a network to solve a given problem involves enumerating
all units, the connections between them, and setting the weights on those connections.
The first two tasks are commonly solved in an ad hoc or heuristic manner, while the
final task is usually accomplished with the aid of a learning algorithm, such as
backpropagation. Backpropagation [3], [5] is a supervised learning technique that
performs gradient descent on a quadratic error measure to modify connection weights.
A network begins with small random weights on its connections and is trained by
comparing its response to each stimulus in the training set with the correct one and
altering weights accordingly. The learning algorithm introduces new design variables,
such as the parameters to control rate of descent.
Genetic
Algorithm
P
o
p
ulation
Network
Performace
Evaluation
Sampling &Synthesis
of Network
„
Blue
p
rints“
blueprint fitness
estimates
instalation
,
N
ew, Untrained Network
testing
Trained Network
Training
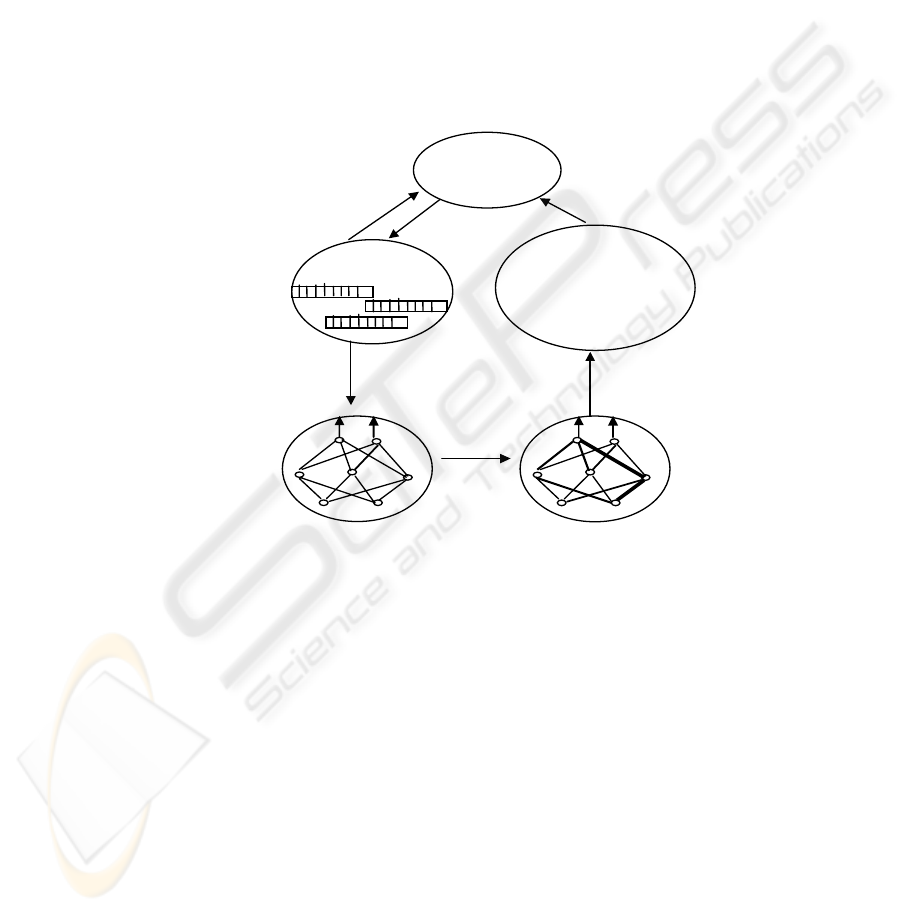
Fig. 1. A population of „blueprints“ designs for different neural networks - is cyclically
updated by the genetic algorithm based on their fitness scores. Fitness is estimated by
instantiating each blueprint into an actual neural network, training, and then testing the network
on the given task.
We use the genetic algorithm [2], [4] to search a space of possible neural network
architectures. In most of these experiences, the system begins with a population of
randomly generated networks. The structure of each network is described by a
chromosome or genetic blueprint - a collection of genes that determine the anatomical
proprieties of the network structure and the parameter values of the learning
algorithm. We use backpropagation to train each of these networks to solve the
problem and then evaluate the fitness of each network in a population. We define
fitness to be a combined measure of worth on the problem, which may take into
account learning speed, accuracy, and cost factors such as the size and complexity of
the network. Network blueprints from a given generation beget offspring according to
4

a reproductive plan that takes into consideration the relative fitness of individuals. In
this respect, application of the genetic algorithm is little different from any other
function optimalization application. A network spawned in this fashion will tend to
contain some attributes from both of its parents. A new network may also be a mutant,
differing in a few randomly selected genes from a parent. Novel features may arise in
either case: through synergy between the attributes of parents or through serendipitous
mutation. The basic cycle is illustrated in Figure 1 [2]. This process of training
individual networks, measuring their fitness, and applying genetic operators to
produce a new population of networks is repeated over many generations. If all goes
well, each generation will tend to contain more of the features that were found useful
in the previous generation.
2 Encoding strategies for neural network topology
We address two major shortcomings of this heuristic approach here. First, the space
of possible artificial neural network architectures is extremely large and most of
applications are unexplored. Second, what constitutes a good architecture is
dependent on the application. Both the problem that is to be solved and the constraints
on the neural network solution need to be considered, but at present we have no
techniques or methods for doing so. Optimal architecture is necessary achieved by
amount of manual trial-and-error experimentation. The problem of optimising neural
network structure for a given set of performance criteria is a complicated one. There
are many variables, both discrete and continuous, and they interact in a complex
manner. The evaluation of a given design is a noisy affair, since the efficacy of
training depends on starting conditions that are typically random. In short, the
problem is a local application for the genetic algorithm that is used to synthesise
appropriate network structures and values for learning parameters. Thumb rules like:
“the harder the problem the more units you need“ are of little practical use to the
design problem. It is known that a neural network with at least one hidden layer can
approximate every function. Almost always a fully interconnected architecture is
used. But what is the optimal number of units and their organization into layers? With
the exception of some simple task (e.g. the XOR-problem) humans cannot foresee the
optimal network topology.
Such complex spaces cannot be explored efficiently be enumerative, random or
even heuristic knowledge-guided search methods. In contrast, the adaptive features of
genetic algorithms (building blocks, step-width control by crossover) provide a more
robust and faster search procedure. Additionally, it is easy to speed-up the genetic
search by means of parallel processing.
Before we discuss the differences between several approaches we want to give a
basic genetic algorithm for topology optimization, which is common to all these
approaches. It is assumed that two representations of the networks are distinguished:
A) genotypes, which are modified by the genetic algorithm′s operators (e.g. mutation
and crossover); B) phenotypes, which are trained by a conventional learning
procedure (e.g. backpropagation) used for performance evaluation or selection.
Roughly two basic representation schemes can be distinguished: low-level genotypes
5

and high-level genotypes. While the first one is transparent and easy to use, there are
two variants of second representation scheme.
Low-level genotypes. Low-level genotypes directly code the network topology. Each
unit and each connection is specified separately. In [6] the following classification of
the encoding strategies of a neural network topology is proposed (the classes are
roughly ordered to the complexity of the strategies), e.g. direct encoding strategies:
− Connection-based encoding. The genome is a string of weight values or pure
connectivity information. The requires a fixed maximal architecture, which is
typically either fully-connected or layered [7]:
− Node-based encoding. The genome is a string or tree of node information. The
code for each node may include relative position, backward connectivity, weight
values, threshold function and more. An advantage over previous approach is that
more flexibility can be obtained by using nodes as basic units. The literature [8]
describe the genetic programming paradigm, which genetically breeds populations
of computer programs to solve problems, where the individuals in the population
are hierarchical compositions of functions and arguments of various sizes and
shapes (i.e. LISP symbolic expressions: S - expression).
− Layer-based encoding. With layer-based encoding we can obtain larger networks
[9]. The encoding scheme is a complicated system of descriptions of connectivity
between a list of layers.
− Pathway-based encoding. Pathway-based encoding is proposed in [10], [11] for
recurrent neural network. The network is viewed as a set of paths from an input to
an output node.
High-level genotypes. High-level genotypes are more complex coded representations
of network architectures. They can be further divided into parametric and recipe
genotypes. There are the networks splited into modules of units which are specified
by parameters and which are coupled by parametric connectivity patterns, in
parametric genotypes. Even through this representation is more compact and thus well
suited to code large network architectures, it is difficult to choose the relevant
parametric shapes.
− The graph generation grammar (GGG) developed by [13] is an early grammar
encoding method based on context-free and deterministic Lindenmayer systems,
e.g. L-systems [12]. The grammar contains productions rules in the special form.
− Nolfi and Parisi in [14] described a method for encoding neural network
architecture into a genetic string, which is inspired by the characteristics of neural
development in real animals. The neurons are encoded with coordinates in a two-
dimensional space. The mapping from genes to neurons is direct in a sense, but the
connections are grooving in a special manner.
− In [15] are proposed main theoretical advantages of the use of L – systems to code
network topologies over “blueprint representations” where the evolutionary
algorithm specifies every single connection in neural networks. They used a
version of L - systems to grow the networks (e.g. the context-sensitive L - system
to rewrite neurons and modules of neurons). Here is each neuron/module by
6

default connected to the next adjacent neuron/module, and missing connections are
denoted by comma.
− Channon and Damper in [16] investigated evolving of behaviors of artificial life
creatures with natural selection. They decided to evolve neural networks and they
used L-systems for encoding of the topology. Precisely, a context-free L - system
was designed for the evolution of neural networks. Specific attention was paid to
producing a system in which children’s networks resemble aspects of their parents.
− In [17] is proposed a method based on L-system that directs neural mass growth
inspired in biology. Rules are then applied in 2-dimensional cell matrix, instead of
a string.
− Gruau´s [18] cellular encoding method uses a grammar tree to encode a cellular
developmental process to grow neural networks. The decoding starts from a
network with a single hidden “cell” that is connected all input and output neurons
of the network. The cell starts reading the grammar tree from its root. The nodes of
the tree are instructions that control how the cell is divided, etc. The child cells of a
differentiate by moving their “read-heads” to different branch of the grammar tree.
Over the last decade many systems have been developed that evolve no only a neural
network topology but both the topology and the parametric values of a neural network
[19], [20] etc.
3 Theoretical basis
We can choose any combination of the n hidden neurons to flip their weight signs so
there are (see Formula 2) structurally different but functionally identical networks
generated by this transformation.
n
i
n
i
n
⎛
⎝
⎜
⎞
⎠
⎟
=
=
∑
2
0
(2)
Suppose that we have a network with h
1
h
2
... h
n
as hidden nodes. The mapping
implemented by the network does not change if a particular hidden node with all its
incoming and outgoing weights is exchanged with another neuron and its weights. For
instance the networks h
1
h
2
... h
n
and h
2
h
1
... h
n
are equivalent, even though the first
and second neuron have changed their position in the hidden layer. Obviously we can
permute any of the n neurons so the total number of functional equivalent networks
by this transformation is n!.
Since the two transformations are independent of each other, there is a total of
2
n
n! functional equivalent but structurally different networks. Recently it has also
been proven that at least in the case of a single hidden layer, one output neuron and a
tangent hyperbolic transfer function the weights within this group of symmetries is
unique, so there are exactly 2
n
n! redundant networks for a specific mapping.
Suppose a we would tell that h hidden units and l hidden layers are necessary for a
given problem. Now, we have to distribute the hidden units into these layers. We will
derive a recursive formula which allows to compute the number of possible partitions
p(h,l). It is evident that:
7

1. If l = 1 or if h = l then p(h,l) = 1.
2. If h < l then p(h,l) = 0, because empty partitions are not reasonable.
3. If h > l we get p(h,l) = p(h - 1, l -1) + p(h - 1, l).
By this formula we can compute the number of possible partitions from that number
of a less complex architecture with h - 1 units. The first term counts the number of
partitions if the boundary of an additional layer separates the additional unit itself.
The second term means that the additional unit is placed into the last hidden layer of a
less complex architecture which has already l layers.
If we have decided for a specific partition we are confronted with the problem of
optimizing connectivity. For h hidden units the number of possible connections is
limited by two extreme topologies which are fully interconnected from input layer
(m units) to output layer (n units):
− A topology that has as much as possible hidden layers with one hidden unit each.
We will refer to that topology as TALL.
− A topology that has just one hidden layer. It forms a look-up table and we will
refer to it as WIDE.
While the TALL-architecture contains (see Formula 3) connections, the WIDE-
architecture has only (see Formula 4) connections, but in most practical applications
neither the TALL - nor the WIDE - architecture will be best suited. Thus, have to find
a connectivity pattern, which is adapted to a particular task.
()
C
hh
hmn mn
T
=
−
+⋅ + + ⋅
2
2
(3)
(
)
Chmnm
W
=⋅ + +⋅n
(4)
4 Conclusion
Genetic algorithms are an effective optimisation, search and machine learning
technique, suitable for a large class of problems, especially for NP-complete state
space problems, which cannot easily be reduced to close form. Genetic algorithms
have been applied largely to the problem of training a neural net, as an alternate
technique to more traditional methods like backpropagation.
8
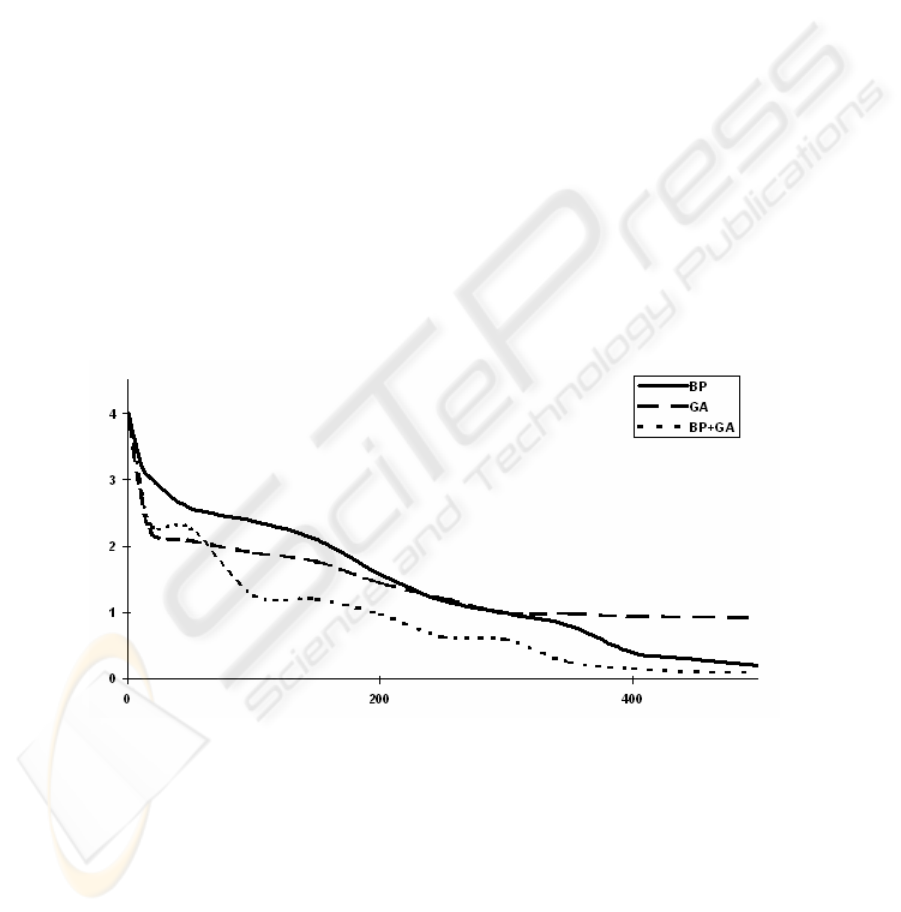
Neural network adaptation. Neural networks solve XOR problem that is not linearly
separable and in this case we cannot use neural network without hidden units. Each
network architecture is 2 - 2 - 1 (e.g. two units in the input layer, two units in the
hidden layer, and one unit in the output layer). The nets are fully connected. If is the
XOR problem solved with genetic algorithm (GA), we need the following parameters:
number of generation was 500, probability of mutation is 0.01 and probability of
crossover is 0.5. The initial population contains 30 neural networks with randomly
generated weight values. Every weight value is written in a code as well as in [21].
Genetic operators (mutation and crossover) also are defined in [21]. History of the
average error function of the whole population during calculation is shown in the
Figure 2. Global search such as genetic algorithms are usually computationally
expensive to run. If the XOR problem is solved with the method backpropagation
(BP), we need the following parameters: learning rate is 0.4 and momentum is 0.1.
History of its error function during whole calculation is shown in the Figure 2. There
is shown an average value of the error function, because the adaptation with
backpropagation algorithm was applied 30 during 500 cycles. If the XOR problem is
solved with a method that combines genetic algorithm and backpropagation, then all
parameters and genetic operators are the same as stated above. And besides that we
have to define the following parameters: number of backpropagation´s iterations is 10
and probability of backpropagation is 0.2. If the input condition of backpropagation is
fulfilled (e.g. if a randomly number is generated, that is equal to the defined constant),
all individuals are then adapted with 10 cycles of BP. History of the average error
function of the whole population during calculation is shown in the Figure 2.
iteratio
Error
Fig. 2. History error function during calculation, where BP is adaptation with backpropagation,
GA is adaptation with genetic algorithm, BP+GA is adaptation with method that combines
genetic algorithm and backpropagation.
This paper also introduces theoretical proposes of neural network configuration by
using genetic algorithms [1], [7], [8], [9] etc. In this participation has been done
simple initial study on neural network optimization by means of evolutionary
9
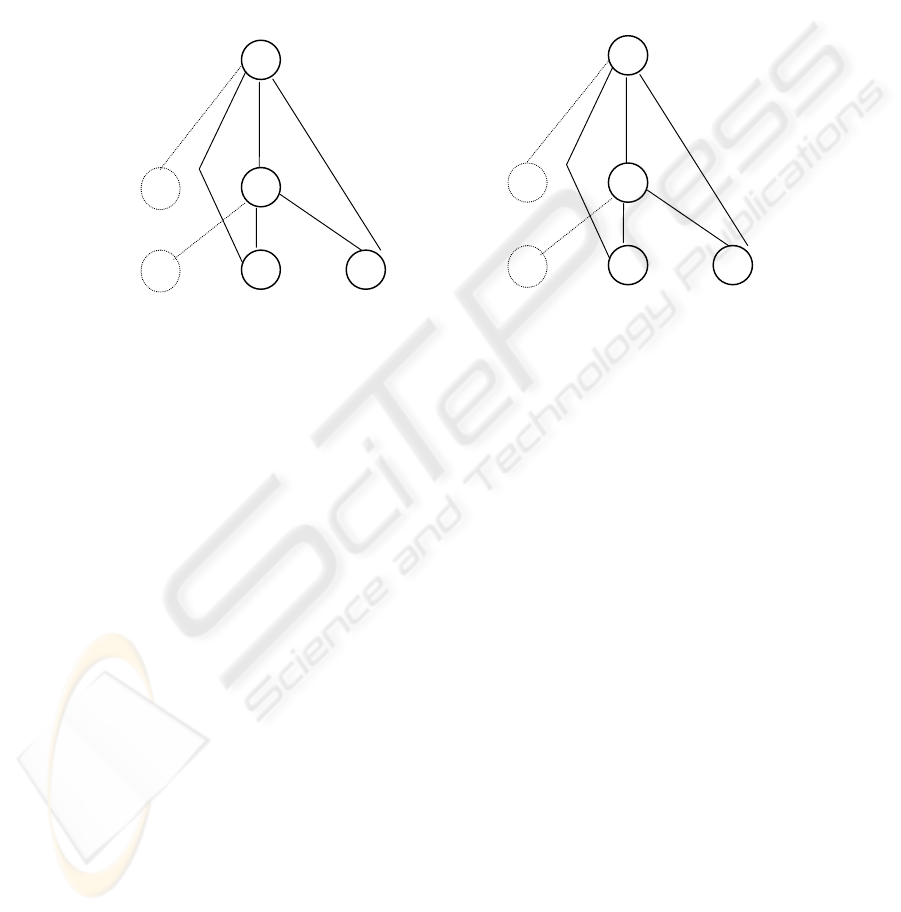
techniques and given positive results has shoved that evolutionary techniques can be
used in this way. In the future more complex study on neural network optimization
are going to be done by means of another evolutionary algorithms.
Neural network architecture. Neural networks solve XOR problem. The Figure 3
illustrates the best representation of neural network for the solution of XOR problem
(a) that was found with genetic algorithm [21] and its following adaptation with
backpropagation (b).
-6.6
10.3
-6.2
-12.7
-7.2
-8.8
-2.2
-7.2
11.2
-7.1
-15.5
-7.5
-7.9
-3.5
1
1
1
1
bias
bias
bias
bias
(a)
(b)
Fig. 3. The best representation of neural network for solution of XOR problem with genetic
algorithm (a) and its following adaptation with backpropagation (b).
References
1. Arena, P. - Caponetto, R. - Fortuna, L. - Xibilia, M.G.: M.L.P. optimal topology via genetic
algorithms. Proceedings of the international conference in Innsbruck, pp. 671-674, Austria
1993.
2. Beale, R. - Jackson, T.: Neural Computing: An Introduction. J W Arrowsmith Ltd, Bristol,
Greit Britain 1992.
3. Goldberg, D. E.: Genetic algorithm in search optimalization and machine learning.
Addison-Wesley, Reading., Massachusets 1989.
4. Herz, J. - Krogh, A. - Palmer, R. G.: Introduction to the Theory of Neural Computation.
Addison Wesley Publishing Company, Redwood City 1991.
5. Lawrence, D.: Handbook of genetic algorithms. Van Nostrand Reinhold, New York 1991.
6. Köhn, P. Genetic encoding strategies for neural networks. Master’s thesis, University of
Tennessee, Knoxville, IPMU, 1996.
7. Maniezzo, V. Searching among search spaces: Hastening the genetic evolution of
feedforward neural networks. In R. F. Albrecht, C. R. Reeves, and N. C. Steele, editors:
Artificial Neural Nets and Genetic Algorithms. Springer-Verlag, pp. 635-643 (1993).
8. Koza, J. R. and J. P. Rice. Genetic generation of both the weights and architecture for a
neural network. In Proceedings of the International Joint Conference on Neural Networks,
Volume II, IEEE Press, 1991.
10

9. Harp, S. A., Samad, T., and Guha, A. Towards the genetic synthesis of neural networks. In
J. D. Schaffer, Ed. San Mateo eds.: Proc. of the Third Intl. Conf. on on Genetic Algorithms
and Their Applications. CA: Morgan Kaufmann pp. 360—369, (1989).
10. Jacob, C., Rehder, J. Evolution of neural net architectures by a hierarchical grammar-based
genetic system. In Proceedings of the International Joint Conference on Neural Networks
and Genetic Algorithms, Innsbruck, pp. 72-79. (1993
11. Angeline, P. J., G. M. Saunders, and J. B. Pollack. An evolutionary algorithm that constructs
recurrent neural networks. IEEE Transactions on Neural Networks, 5: 54-65, 1993.
12. Lindenmayer A.: Mathematical models for cellular interaction in development I, II. Journal
of Theoretical biology (18): 280-315 1968.
13. Kitano, H. Design neural network using genetic algorithm with graph generation system.
Complex systems,(4): 461-476, 1990.
14. Nolfi, S., Parisi, D. Genotypes for neural networks. In M. A. Arbib, editor: The Handbook
of Brain Theory and Neural Networks. MIT Press 1995.
15. Boers, E.J.W., Kuiper, H., Happel, B.L.M., and Sprinkhuizen-Kuyper, I.G.. Designing
modular artificial neural networks. In H.A. Wijshoff, editor: Proceedings of Computing
Science in The Netherlands. pp. 87-96, Amsterdam, 1993. SION, Stichting Mathematisch
Centrum. Amsterdam 1993.
16. Channon, A. D. and Damper, R. I. Evolving novel behaviors via natural selection, In Adami,
C., Belew, R. K., Kitano, H. and Taylor, C. E., eds.: Alife IV. Sixth International
Conference on Artificial life. , pp. 384-388. Bradford Books/MIT Press, Cambridge, MA,
1998.
17. Aho, I., Kemppainen, H., Koskimies, K., Mäkinen, E., and Niemi, T. Searching neural
network structures with L systems and genetic algorithms. International Journal of
Computer Mathematics, 73 (1): 55-75, 1999.
18. Gruau, F., D. Whitley, and L. Pyeatt. A comparison between cellular encoding and direct
encoding for genetic neural networks. In J. R. Koza, D. E. Goldberg, D. B. Fogel, and R. L.
Riolo, editors, Genetic Programming 1996: Proceedings of the First Annual Conference, pp.
81-89, Cambridge, MA, MIT Press, 1996.
19. Opitz, D. W. and J. W. Shavlik. Connectionist theory refinement: Genetically searching the
space of network topologies. Journal of Artificial Intelligence Research, 6: 177-209, 1997.
20. Yao, X. and Y. Liu. Towards designing artificial neural networks by evolution. Applied
Mathematics and Computation, 91(1): 83-90, 1996.
21. Volna, E.. Learning algorithm which learns both architectures and weights of feedforward
neural networks. Neural Network World. Int. Journal on Neural & Mass-Parallel Comp. and
Inf. Systems. 8 (6): 653-664, 1998.
11
