Grinding Forces Prediction Based Upon Experimental
Design and Neural Network Models
Ridha Amamou
1
, Nabil Ben Fredj
1
, Farhat Fnaiech
2
1
Laboratoire de Mécanique Matériaux et Procédés, Ecole Supérieure des
Sciences et Techniques de Tunis,
2
Centre de Recherche en Productique, Ecole Supérieure des Sciences et
Techniques de Tunis,
5 Av. Taha Hussein, Montfleury, 1008 Tunis, Tunisia
Abstract. The results presented are related to the prediction of the specific
grinding force components. The main problems associated with the prediction
capability of empirical models developed using the design of experiment (DOE)
method are given. In this study an approach suggesting the combination of
DOE method and artificial neural network (ANN) is developed. The inputs of
the developed ANNs were selected among the factors and interaction between
factors of the DOE depending on their significance at different confidence
levels expressed by the value of α%. Results have shown particularly, the
existence of a critical input set which improves the learning ability of the
constructed ANNs. The built ANNs using these critical sets have shown low
deviation from the training data and an acceptable deviation from the testing
data. A high prediction accuracy of these ANNs was tested between models
constructed using the developed approach and models developed by previous
investigations.
1 Introduction
Because of the importance of the grinding forces regarding to the process outputs
including wheel wear and surface integrity, many attempts were made to model its
normal and tangential specific components. However, analyses of the obtained
models have shown that the theoretical modeling [1] exhibits shortcomings from a
quantitative aspect because the permanent changes on shapes and on density of the
cutting edges cannot be clearly taken into account by these models. This suggests the
use of simplifying hypotheses affecting the reliability of these models and limiting
their employment to off-line prediction tasks. In contrast, empirical models, such as
the regression analysis model [2, 3, 4], the fuzzy logic model [5, 6] and the neural
network model [7-11] have, generally, shown satisfactory prediction accuracy,
particularly useful for the on-line response evaluation and control. In many cases, data
from design of experiment (DoE) were used to establish the regression models or to
develop the fuzzy rule sets or to train the neural networks. Indeed, the DoE method
offers the possibility to study the effects of several factors at one time and to
investigate the inter-relationships between these factors, while conducting a relatively
limited number of experiments [12].
Amamou R., Ben Fredj N. and Fnaiech F. (2005).
Grinding Forces Prediction Based Upon Experimental Design and Neural Network Models.
In Proceedings of the 1st International Workshop on Artificial Neural Networks and Intelligent Information Processing, pages 122-131
DOI: 10.5220/0001194101220131
Copyright
c
 SciTePress

However, this method has to be used with awareness, especially when it is applied for
response minimization tasks. In fact, it was remarked that in many cases, the
regression analysis models established by using the DoE were unable to predict an
appropriate minimal response value [13].
This constitutes serious limitation of this method, particularly, for on-line process
control, where the predicted optimal values have to be determined with high accuracy
as they are continuously compared to targets to maintain the desired level of the
outputs.
These inconveniences give rise to the need to develop improved methods with
enhanced prediction capability. In this paper, feed forward neural networks using the
Bayesian regularization were developed. The goal was to train ANNs to include the
most important factors and interactions between factors affecting the surface
roughness in order to make accurate and consistent predictions for new combinations
of values for these factors. This was made by considering the extrapolation beyond
the training data. The developed ANNs were trained using an experimental data set of
a 48 runs factorial design and the best set of variables inputs, the number of neurons
and the ANNs structures selection criteria were discussed. The performance of the
developed ANNs on predicting the specific cutting force components F’
n
and F’
t
within the range of the factors levels fixed by the factorial design was compared to the
statistical multiple regression models obtained directly using the design of experiment
method. Here F’
n
and F’
t
are respectively the normal and the tangential specific
components of the grinding force.
2 ANN approach
Even though several learning methods have been developed [7-11, 14-19], the back
propagation method has been proven to be successful in applications related to
surface integrity prediction [7, 8, 10, 18]. However, the effect of the neural network
inputs selection was not elucidated sufficiently. Indeed, even though it is known that
the selected inputs of the ANNs is an important parameter controlling the outputs
prediction accuracy [8, 16 19], previous studies which have used the DoE data to train
the ANNs, have also used the independent variables of the DoE as inputs of the
developed ANNs. On the other hand the major problem encountered in the use of
ANNs is over fitting [20]. A neural network can predict correctly the trained data set
but it is unable to generalize for other input data. Consequently, the training error
function E is modified to include not just the sum of square errors E
a
but also the sum
of squares of the network weights and biases E
w
. This approach is called the weight
decay regularization [20]. This modification forces the network to have smaller
weights and biases and decrease the tendency of a model to over fit the training data.
The modified error function to be minimized is:
wa
EEE )1( θθ −+=
(1)
where θ is the weight decay parameter. The difficulty with regularization is in
assigning an optimum value of θ. If the selected weight decay parameter is too large,
so that overfitting may accrues. On the other hand if it is too small the network will
not adequately fit the training data. Finding the optimum value for the weight decay
123

parameter that is appropriate for the training data is therefore an important task. In
this investigation, the weight decay parameter was determined by the Bayesian
framework. In this case all weight and biases of the network are assumed to be
random variables with Gaussian distribution. The weight decay parameters are related
to the unknown variances associated with these distributions.
In this study, a 48 runs DoE rotatable central composite design was developed. The
data of this experimental design were utilized to train a one hidden layer back
propagation neural network. In fact, previous investigations have proven that this
architecture is enough for the majority of applications [7-11, 16-19].
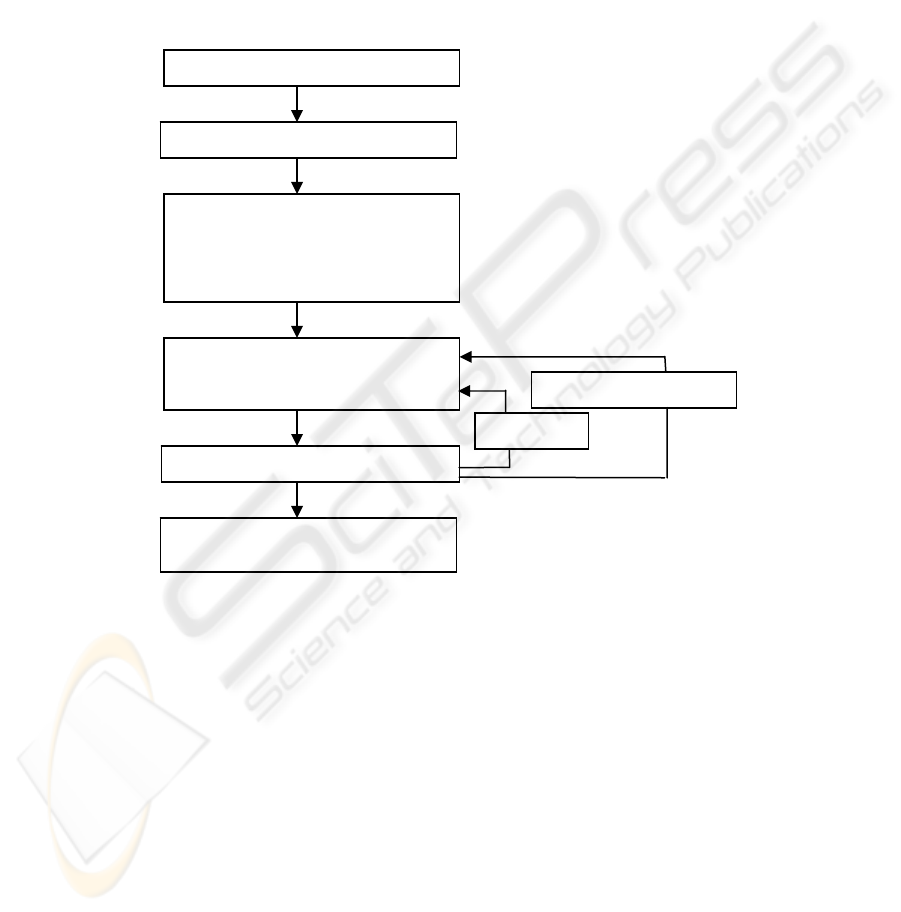
Fig. 1. Algorithm for ANN Training and selection
As for the inputs selection, it was discussed based on the statistical significance of the
independent variables or interactions between these variables obtained from the
quadratic regression models developed using the data of the 48 runs DoE according to
the algorithm shown in figure 1. The point in this algorithm is that the ANN will be
also trained for learning the factors interactions effects. In fact, the effects of
interaction between factors can be in some cases, more significant than the effects of
the factors. M. Thomas et al [3] have shown in their study related to the prediction of
the surface roughness generated by the cutting process that the effect of the
interaction between the feed rate f and the depth of cut (a) is more significant than the
effect of the individual factors. On the other hand, as good generalization of the
developed ANNs requires that their inputs contain sufficient information pertaining to
the output, so that an accurate mathematical function relating the outputs to the inputs
Desi
g
n an ex
p
eriment
Establish the re
g
ression model
Classify factors and interaction
in an increasing order of the p_value
and corresponding te α%
Train the ANN using inputs
corresponding to α=
α
ι
% and number of
neurons n=n
j
Save results and
p
erformances
n=n
j
+1
α
ι
=
α
ι
+ increment
Select the most efficient ANN
124

can be established [21], using the interactions between factors as additional inputs for
the ANNs improves this accuracy. Moreover, as the Multilayer perceptron (MLP)
architectures are good at ignoring both redundant and irrelevant inputs [19], non-
pertaining interactions, which are used as inputs for the developed ANNs will not be
considered automatically. Nevertheless, as the training time of the developed ANNs is
widely affected by the number of inputs, therefore, it is important to distinguish the
significant interactions and to use them as additional inputs. This fact is well
considered by the algorithm of figure 1.
The number of epochs was set to 200 and the ANN performances were evaluated by
the training error MSE, training time (s), percentage of deviation from training data,
percentage of deviation from testing data, and the values of the optimal outputs and
the corresponding inputs combinations.
3 Experimental Set-up and design
All the grinding tests were realized in down cut plunge surface grinding mode using a
Teknoscuola RT600 grinding machine. Grinding wheels were dressed using a single
point diamond dresser with a constant gross feed (0.2 mm/rev). The workpieces
dimension was 100
L
x30
H
x15
W
mm. The grinding force components were measured
using a piezo-electric transducer based type dynamometer (kistler 9257A). Three
workpiece materials having different structures and mechanical properties were
selected, 42CrMo4, 90MnCrV8 and X160CrMoV12. Chemical composition and
hardness of these materials are given in table 1. The selection was made based on the
wide industrial application of these materials.
Table 1. Chemical composition of the used material
material C Si Mn Cr Mo P S Hardness HR
C
42CrMo4 0.41 0.28 0.77 1.02 0.25 0.02 0.03 36
90MnCrV8 0.9 _ 2.0 0.4 0.7 _ _ 60
X160CrMoV12 1.55 _ _ 12.0 0.7 _ _ 63
Concerning the grinding parameters, table speed (v
w
), depth of cut (a), grinding wheel
grain mesh size (#), dressing depth (a
d
) and the number of passes (N
p
) were selected.
The selected values of the process parameters, given in table 2, cover conditions
related to both coarse and fine grinding. For experiments a 48 runs DoE rotatable
central composite design was selected and experiments were conducted in a random
order. Three factorial experimental designs using the L
27
[3
5
] standard table were used
for testing the prediction performances of the regression models and the different
ANN structures selected in this study. Here, the material was not considered as an
independent factor and the 27 testing experiments were repeated for each material
type.
125

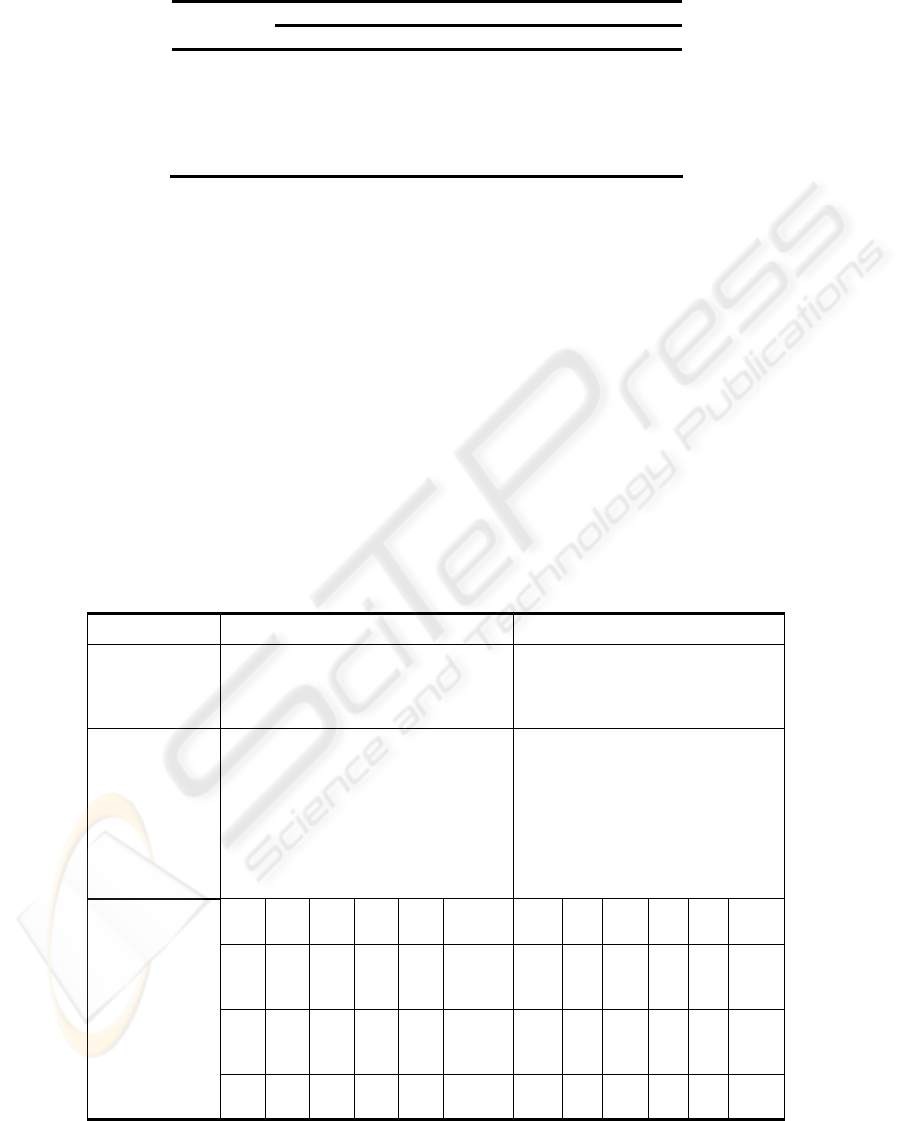
Table 2. Process parameters and values
Factor Level
1 2 3
Material
v
w
(m/min)
a (mm)
N
p
a
d
(mm)
#
42CrMo4
1
0.050
2
0.010
46
90MnCrV8
5.5
0.100
11
0.020
60
X160CrMoV12
10
0.150
20
0.030
80
4 Results and discussions
4.1 Statistical results
Table 3 summarizes the statistical performances of the regression models developed
for F’
n
and F’
t
. This table shows, particularly, an important average percentage of
deviation from the testing data calculated for the three kinds of materials. Moreover,
negative optimal values of F’
n
and F’
t
are calculated. It can be notice that the
regression model of F’
n
and F’
t
established using the DoE presents low capability to
predict the optimal output value rather than the corresponding factors level. Indeed,
the combinations corresponding to the optimal values for F’
n
and F’
t
are in good
correlation with the results of previous studies [22,23]. This constitutes a serious
limitation of the prediction performances of the regression models established in this
study.
Table 3. Summary of the statistical performances of the DoE multiple regression models.
Results Model for F’
n
Model for F’
t
Percentage
deviation of
the training
data
51,58% 44,95%
Percentage
deviation of
the testing
data:
• 42CrMo4
• 90MnCrV8
• X160CrMo
V12
24,1%
28,01%
28,032%
23,31%
37,05%
35,62%
V
w
a N
p
a
d
# F’
n min
V
w
a N
p
a
d
#
F’
t
min
1 50 2 30 46 -1,273 1 50 2 30 46 -
0,74
4
1 50 2 28 46 -1,341 1 50 2 30 46 -
0,55
8
Grinding
conditions for
the minimal
value:
• 42CrMo4
• 90MnCrV8
• X160CrMo
V12
1 50 2 30 46 -0,045 1 50 2 10 46 0,06
8
126

4.2 ANN results
4.2.1 6-n-1 structure
At first, the common method for establishing ANN’s architecture was used. This was
realized by selecting the same inputs for the developed ANN as those selected for the
DoE. Hence, a 6-n-1 structure was constructed; with n is the number of neurons in the
hidden layer. The value of n was varied from 2 to 40 and the average
MSE error of
the 39 constructed artificial neural networks was 0.023 in the case of F’
n
and 0.0037
in the case of F’
t
. When considering the structure 6-5-1 for which the lowest training
error MSE (MSE=1.04e-03) and deviations from testing data were computed, the
calculated deviations from the training data were 0.84% for F’
n
and 0.47% for F’
t
.
However, the percentages of deviations from the testing data for F’
n
were 26.82% for
42CrMo4, 22.71% for 90MnCrV8 and 23.17% for X160CrMoV12. Concerning the
specific tangential force F’
t
, the calculated deviations from the testing data were
19.42% for 42CrMo4, 20.87 for 90MnCrV8 and 23.34% for X160CrMoV12. These
high deviations express poor generalization capability of the ANN structures with 6
inputs. Therefore, more training data are needed to improve the prediction efficiency
of this neural network architecture when extrapolation beyond the training data is
considered.
4.2.2 x-n-1 structure
For improving the prediction capability of the ANNs, the number of inputs was
varied. Therefore, instead of selecting the same inputs as the DoE, the factors and the
second order interactions between factors were selected as inputs. Figure 2, show the
relation between the averages
MSE
error for the 39 artificial neural networks
structures constructed using the significant factors and interactions at different
confidence levels for F’
n
et F’
t
. A clear improvement of the learning capability of the
constructed artificial neural networks can be seen from this figure as an important
reduction of the average
MSE
error could be realized. Moreover, these figures put in
evidence the existence of a threshold value of α% for which no significant learning
improvement can be realized by increasing the number of inputs. Here a threshold
value about 50% was observed for F’
n
and F’
t
.
On the other hand, as in this work we are particularly interested on the grinding force
minimization, extrapolation beyond the training data have to be considered. Hence,
calculation of a global error (E
g
) expressing the deviation of the predicted values
using the developed neural networks from the testing data sets is required to valid the
results of this investigation.
This error is composed of two terms: the bias which measures the extent to which the
average predicted output, over all testing data sets, of the network function differs
from the experimental values and the variance which measures the extent to which
the network function is sensitive to particular choice of data set [18]. As in this
investigation 27 testing experiments were conducted for each material (n=81) and 39
different networks (m=39) were trained for each input set, the expressions of the bias
and the variance can be written in the following forms [20]:
127

{}
{}
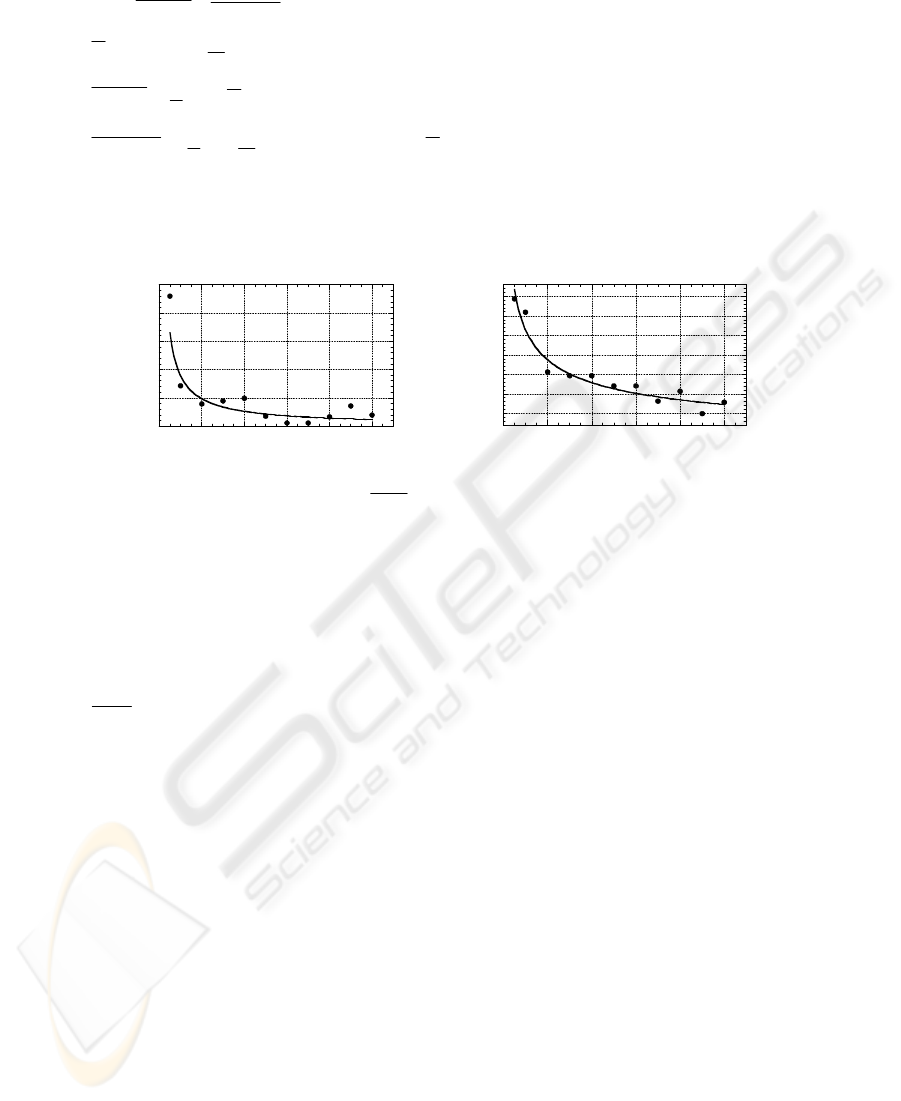
)5(])()((
1
[
1
var
)4(])()([
1
)(
)3()(
1
)(
)2(var)(
1
2
1
1
2
exp
2
1
2
∑∑
∑
∑
==
=
=
−=
−=
=
+=
m
i
k
predicted
kpredicted i
n
k
n
k
kerimentalk
predicted
m
i
predicted i
predicted
g
XFXF
mn
iance
XFXF
n
bias
XF
m
XF
iancebiasE
Here F represents F’
n
or F’
t
depending on the considered output and X and X
k
are the
input sets.
0
0.0005
0.001
0.0015
0.002
0.0025
0 0.2 0.4 0.6 0.8 1
Average errors (mse)of the ANNs
for F'n
confidence level α %
(a)
1 10
-5
1.5 10
-5
2 10
-5
2.5 10
-5
3 10
-5
3.5 10
-5
4 10
-5
00.20.40.60.81
Average error (mse) of the ANNs
for F't
Confidence level α %
(b)
Fig. 2. Relation between the average
MSE
errors of the 39 ANN structures and α%: (a) F’
n
and (b) F’
t
Figure 3 gives the relation between the average error E
g
for F’
n
and F’
t
respectively at
different confidence levels. It can be seen from these figures that for the testing data
sets selected in this investigation, the minimum average error E
g
occurs at α around
50% for the specific normal component F’
n
and 40% for F’
t
. However, the input set
which have to be selected for the developed ANNs is the set that offers,
simultaneously, high leaning performance of the training data characterised by low
MSE and good generalisation characterized by low value of E
g
. Therefore, inputs sets
corresponding to α=50% have to be retained for the ANNs related to F’
n
and F’
t
.
Therefore, the corresponding inputs are used to train the artificial neural networks and
the best structure offering the lowest deviation from the training and testing data were
16-18-1 for F’
n
and 19-11-1 for F’
t
. The full performances of these structures are
given in table 4. This table shows particularly positive values for the predicted
minimal cutting force parameters F’
n
and F’
t
. Here 0% and 0.028% deviations from
the training data were calculated respectively for F’
n
and F’
t
. The percentages of
deviations from the testing data for F’
n
were 7.6% for 42CrMo4, 8.55% for
90MnCrV8 and 7.46% for X160CrMoV12. These deviations are clearly lower than
those calculated using the 6-5-1 structure. Concerning the specific tangential force F’
t
,
the calculated deviations from the testing data were 7.32% for 42CrMo4, 8.58% for
90MnCrV8 and 7.11% for X160CrMoV12.According to these findings, it can be
concluded that a factor or an interaction between factors, which is statically not
significant in the case of the DoE, can be a significant input for the ANN.
128

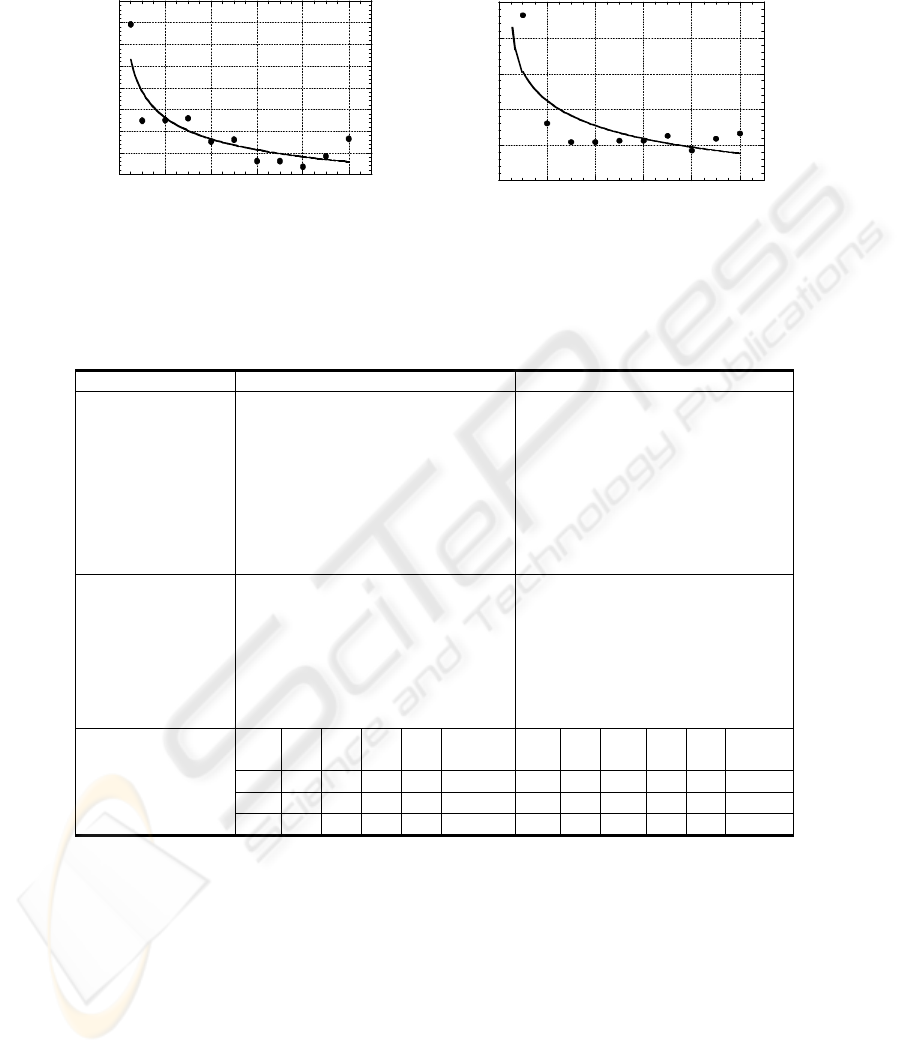
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
00.20.40.60.81
Average error Eg for F'n
confidence level α %
(a)
0.15
0.2
0.25
0.3
0.35
0.4
00.20.40.60.81
Average error Eg for F't
confidence level α %
(b)
Fig. 3. (a) Relation between the confidence level α% and the average error E
g
: (a) F’
n
and (b)
F’
t
Table 4. Summary of the selected ANN performances
5 Conclusions
In this paper an approach combining the application of the design of experiment
(DoE) and the neural network methods was developed to establish accurate models
for specific grinding forces prediction. This approach uses data of the DoE to train
artificial neural network for which the input set is composed of significant factors and
interaction between the factors of the DoE. The significance was evaluated based on
Results Model for F’
n
(16-18-1) Model for F’
t
(19-11-1)
Number of inputs 16 19
Hidden nodes 18 11
Mean Square Error 1.956e-05 5.58e-12
Sum Square Error 8.804e-04 2.51e-10
Running time* (s) 18 34
Training cycles 200 200
Percentage deviation
of the training data
Percentage deviation
of the testing data
for:
• 42CrMo4
• 90MnCrV8
• X160CrMoV12
0%
7.6%
8.55%
7.46%
0.028%
7.32%
8.58%
7.11%
V
w
a N
p
a
d
# F'
n mini
V
w
a N
p
a
d
# F'
t mini
1 50 2 30 46 0,0757 1 50 2 30 46 0,0551
1 50 2 30 46 0,1371 1 50 2 20 46 0,0753
Grinding conditions
for the minimal value
• 42CrMo4
• 90MnCrV8
• X160CrMoV12
1 50 6 10 46 0,3956 1 50 2 10 46 0,0889
129

the Fisher test at different values of the confidence levels α%. When this level
increases, the number of significant factors and interactions increased, and thus the
number of inputs of the ANN increases. Average learning
MSE which express the
average error between the training data and the corresponding predicted values and
the generalization error
Eg
which express the deviation from the testing data have
shown the existence of a critical set of inputs offering the highest prediction capability
of the developed ANNs. By using this approach, substantial improvements of the
prediction capability of the ANNs could be realized comparatively with the prediction
ability of the quadratic models developed using the DoE. On the other hand the
developed ANNs have shown better capability comparatively with the commonly
used structures, which use the DoE factors as inputs.
It was also remarked that the developed ANNs present higher sensibility to the input
variations than the DOE as they can distinguish between particular phenomena
occurring at low and high work speeds. At last, problems related to the minimal
negative predicted value, calculated by using models established with DOE method
could be solved as ANNs respects the output sign.
References
1. H.K. Tönshoff, J. Peters, I. Inasaki, T. Paul, Modelling and Simulation of Grinding Process,
Annals of the CIRP vol. 41, 2, (1992) 677-688.
2. Y. S. Lio, J. T. Huang, H.C. Su, A study on the machining-parameters optimization of wire
electrical discharge machining, J. Mater. Proc. Technol. 71 (1997) 487-493.
3. M. Thomas, Y. Beauchamp, Youssef, A. Youssef, An experimental design for surface
roughness and built-up edge formation in lathe dry turning, Int. J. of Quality Science, Vol.
2 (3), (1997) 167-180.
4. Y. A. Youssef, Comparison of a full factorial experiment to fractional and Taguchi design
in a lathe dry turning operation, Computers in ind. Engng., Vol. 27 (1-4), (1994) 59-62.
5. J. L. Lin, K.S. Wang, B.H. Yan, Y. S. Tarng, Optimization of the electrical discharge
machining process based on the Taguchi method with fuzzy logics, J. Mater. Proc.
Technol., 102 (2000) 48-55.
6. Y. Ali, L.C. Zhang, Estimation of Residual Stress Induced by Grinding Using a Fuzzy
Logic Approach, J. Mater. Proc. Technol. 63 (1997) 875-880.
7. Y.-H. Tsai, J. C. Chen, S.-J. Lou, An in-process surface recognition system based on neural
networks in end milling cutting operations, Int. J. Mach. Tools Manufact., Vol. 39, (1999)
583-605.
8. R. Azouzi, M. Guillot, On-line prediction of surface finish and dimensional deviation in
turning using neural network based sensor fusion, Int. J. Mach. Tools Manufact., Vol. 37
(9), (1997) 1201-1217.
9. T. Warren, L.J. Chen, A neural network approach for grinding process: Modeling and
optimization, Int. J. Mach. Tools Manufact., Vol. 34 (7), (1994) 919-937.
10. N. Zouaghi, Y. Ichida, N. Ben Fredj, N. Kimura, Grinding mode identification of silicon
carbide by using neural network, in: Proceeding of the third international conference on
progress of cutting and grinding Vol. III (JSPE, Osaka, 1996) 342-347.
11. K. M. Tsai, P. J. Wang, Predictions on surface finish in electrical discharge machining
based upon neural network models, Int. J. Mach. Tools Manufact., Vol. 41, (2001) 1385-
1403.
130

12. Douglas C. Montgomery, Design and Analysis of Experiments 3
rd
edition, (Jhon Wiley &
son 1991).
13. Nabil Ben Fredj, Ridha Amamou, Ground Surface Roughness Prediction Based Upon
Experimental Design and Neural Network Models, accepted for publication in Int. J.
advanced Manufacturing Technology.
14. D. H. kim, D. J. Kim, B. Kim, The application of neural networks and statistical methods to
process design in metal forming, Int. J. Adv. Manuf. Technol., Vol.15, (1999) 886-894.
15. D.-C. Ko, D.-H. Kim, B.-M Kim, Application of artificial neural network and Taguchi
method to perform design in metal forming considering workability, Int. J. Mach. Tools
Manufact., Vol. 39, (1999) 771-785.
16. E. Mainsah, D.T. Ndumu, Neural network in surface topography, Int. J. Mach. Tools
Manufact., Vol. 38 (5-6), (1998) 591-598.
17. S.-T Chiang, D.-I Liu, A.-C. Lee, W.-H. Chieng, Adaptive control optimization in end
milling using neural network, Int. J. Mach. Tools Manufact., Vol. 34 (5), (1995) 637-660.
18. T. S. Spedding, Z. Q. Wang, Study on modelling of wire EDM process, J. Mater. Proc.
Technol. 69 (1997) 18-28.
19. S. Haykin, Neural Networks a comprehensive foundation, (Macmillan College Publishing
Company 1994).
20. C. M. Bishop, Neural Networks for Pattern Recognition, Oxford University Press, 1995.
21. M. Sakakura, I. Inasaki, A neural network approach to the decision-making process for
grinding operation, Annals of the CIRP Vol. 41 (1), (1991) 353-356.
22. S. Malkin, Y. Koren, Off-line Grinding Optimisation with a Micro-Computer, Annals of
the CIRP, Vol. 29 (1), (1980) 213-215.
23. S.Malkin, Grinding Technology theory and applications of machining with abrasives, (Ellis
Horwood Ltd. 1989).
131