A Support System for Fisheries
Based on Neural Networks
Alfonso Iglesias
1
, Bernardino Arcay
1
, Alejandra Rodríguez
1
and Manuel Cotos
2
1
University of A Coruña
2
University of Santiago de Compostela
Abstract. This paper presents the foundations of a decision support system for
the localisation of fisheries based on AI techniques. The purpose of such a
system is to reduce the costs of fishing fleets without endangering the
sustainable development of the natural resources. Our data sources are satellite
images (OrbView-2, Series NOAA, Topex/Poseidon), as well as real catch data
obtained from the fishing log of a pilot boat. We have compared neural
networks, ANFIS, and functional networks, and we have exported the results to
a SIG. The best results were obtained for a perceptron trained with the
Backpropagation method.
1 Introduction
In spite of the fact that the exploitation of marine resources is one of the main
economic activities in Spain, recent ecological disasters, quota policies and biological
stops have started to endanger this important sector. An economic activity that is as
competitive as fishing should learn to apply, within a framework of sustainable
development
[1], new technologies such as decision support systems.
Remote sensors are a vital source of information for this type of system. Our
proposal is to use Artificial Intelligence techniques to relate the information that
proceeds from Orb View-2, series NOAA and Topex-Poseidon images on the one
hand, and the capture data on the other hand. Real capture data, provided by a
collaborating boat dedicated to line fishing in the northern Atlantic Ocean, and the
information from remote sensors, allow us to create a training and validation set with
which to compare the results of various predictors that are generally based on
connectionist systems. Valid parameters for our prediction algorithms will allow the
boats to find the best fishing zones, reduce search times for fishing grounds, and
increase the catches within the existing legal boundaries.
2 Methods and data sources
This section explains the foundations of a new support system for fisheries, which
uses the data obtained by various remote sensors and the fishing log of a collaborating
boat to predict catches of a the Prionace Glauca, a pelagic shark species that is also
known as blue shark or quenlla (see
[2]). The main advantages of good prediction are
less fuel expenses and less time spent at sea, which will result in a positive effect of
Iglesias A., Arcay B., Rodríguez A. and Cotos M. (2005).
A Support System for Fisheries Based on Neural Networks.
In Proceedings of the 1st International Workshop on Artificial Neural Networks and Intelligent Information Processing, pages 112-121
DOI: 10.5220/0001194401120121
Copyright
c
 SciTePress

the involved fleets. The developed system can be extended to any marine species for
which we dispose of enough available data to train the system.
Figure 1 shows that the system can be decomposed into three different phases,
whose final purpose is to transmit products that can be sent to the embarked units.
The main purpose of phase 1 is to receive the information from various satellites.
The system consists of an antenna park that captures signals from the NOAA (in low
and high resolution), OrbView-2 (images of the SeaWifs sensor) and Meteosat
satellites. The data are stored in a backup system and distributed to all the computers
that constitute the local network. All these computers have access to the data in order
to visualize and process them. An exhaustive description of this phase can be found in
[1], [2], [3].
Fig. 1. Chart of the Support System for fisheries
The purpose of this work is to use the data that result from phase 1 to elaborate
phase 2:
• Apply digital processing techniques to the initial products in order to
obtain new data with biological meaning, e.g. the following high-pass
filters which can detect the existence of thermic fronts:
o DoG (see [4]).
o Cluster-Shade (see [5]).
• Visualize this information regardless of the used platform.
• Study the sensibility and correlation of the initial data through:
o The analysis of the main components.
o Kohonen’s Self-Organising Maps.
• Calculate the probability of fishing catches according to environmental
parameters obtained through teledetection. We try the following
techniques:
o Networks trained with the backpropagation algorithm.
o Radial Basis Function networks.
o Functional networks.
o Neuro-diffuse inference system (ANFIS)
• Manage all the information efficiently and with a centralized control. To
this effect, we design an appropriate database based on the E-R model.
Data Reception
Initial
Processing
Comunication
users
Obtention
satellite images
Calculation
Predictions
Representation
information
P
hase 1
P
hase 2
P
hase 3
113

During phase 3, our system communicates with the users. The information can be
transmitted to the embarked unit by various communication services such as the
Inmarsat satellite, a global network that provides a large variety of services
(telephone, data, fax, web,…) and is used by many boats for maritime emergency
calls. Thanks to the TUNAFIS 4.2 software, developed by other members of the
Instituto de Investigacións Tecnolóxicas, the users can also send e-mails, manage user
accounts and transfer the information into a graphic interface.
2.1 Data sources
This work is based on images of the NOAA, OrbView-2 and Topex-Poseidon series.
After an initial processing, the input data are the following:
• Surface Temperature or SST (NOAA)
• Thermic Anomaly (NOAA)
• Thermic front (NOAA)
• Superficial chlorophyll concentration (OrbView-2)
• Altimetric Anomaly (Topex-Poseidon)
We eliminated the thermic anomaly, because a sensibility study with Kohonen
networks led to the conclusion that the thermic anomaly does not provide relevant
information, probably because it is redundant with the STT.
Apart from these satellite images, we also dispose of the field data of a
collaborating fishing boat, that uses the palangre method and transmits the initial and
final geographic data of the lance de palangre, and the daily catches for each species
during the years 1998 and 1999.
Our training set therefore consists of four inputs from remote sensors images, and
one output, which is the number of catches of a determined marine species.
2.2 Methods
The absence of mathematical models and a clear set of knowledge rules, as well as the
existence of a set of training data, leads to the use of connectionist systems within the
different Artificial intelligence techniques.
2.2.1 Neural Networks
Neural networks have come a far way since the first publications, but they are
recognized as a versatile discipline with profound roots in neurosciences, psychology,
mathematics, physics, and engineering.
Previous works have confirmed neural networks as an adequate methodology with
reliable results:
- T. Komatsu et al [6] have predicted sardine catches through NN. They used
synaptic weights to analyse the most important physical or biological factor and
obtained satisfactory results. Previous regression models did not result effective due
to the correlation between the input variables.
- D. Aurelle et al [7] used a perceptron with 3 layers and 2 neurons in the hidden
layer, and trained with the error bacpropagation algorithm, to predict fishing data.
114

- M. J. Dreyfus-Leon [8] predicted the behaviour of a fisherman with neural
networks.
- Aussem and Hill [9] predicted the presence of a maligne green alga (Caulerpa
taxifolia) through a multilayer perceptron with supervised training.
- Brosse et al [10] predicted the abundance of fishing grounds in lakes with neural
networks. They compared NN with the Multiple Linear Regression technique and
with an analysis of the main components, and concluded that the NN provide the most
exact predictions.
- Maas et al [11] predict environmental parameters based on temporal series that
correspond to the El Niño phenomenon.
An Artificial Neural Network can generally be defined as a machine that is
designed to imitate the way in which the human brain performs a task or a function;
the neural network is usually implemented with electronic components or simulated
by a computer. The results are obtained by using massive interconnections between
simple processing elements called neurons.
2.2.2 Functional networks
Functional networks are among the tested algorithms. Since they constitute a
relatively recent paradigm, we briefly explain their functioning.
The mid-eighties saw the appearance of extensions of neural networks, such as
networks of a high order, probabilistic neural networks [12], and neural networks
based on “wavelets” [13]. These models however still acted as mere black boxes
without considering the functional structure and the properties of the object that was
being modeled. An essential characteristic of the functional networks is the possibility
to consider functional restrictions that are determined by the properties of the model.
These restrictions lead to a determined topology of the network and therefore to a
system of functional equations.
Castillo et al [14] introduced the functional equations as an extension of the neural
networks. In a simple but rigourous definition, a Functional Network can be described
as a Neural Network in which the weights of the neurons are replaced by a set of
functions. They present, among others, the following advantages [15]:
1) Contrary to neural networks, functional networks can reproduce certain
physical properties that naturally conduct to the corresponding network as long
as they can use an expression with a physical meaning in the functions base. In
our case we do not dispose of this information and can therefore not make use
of this advantage.
2) The network parameters can be estimated by solving a linear equations
system, a rapid and unique solution that is the global minimum of the error
function.
Functional networks have been applied successfully to problems of medical
diagnosis and to conjugated Bayesian distributions. These problems, the solutions
based on functional networks, and the formalisms of the equations and functional
networks, can be found in the book by Castillo et al [15].
A functional network consists of the following elements:
115

1) An input layer of storage units. This layer contains the input data.
2) An output layer of storage units. This layer contains the output data.
3) One or various layers of processing units. These units evaluate a set of
input values that proceed from the previous layer (an intermediate unit or the
input layer), and calculate values that will be considered in the following
layer. Each neuron is associated to a functional neuron that can possess
several arguments or inputs; this allows us to introduce part into each
processing unit part of the mathematical model that helps to explain our
problem.
4) None, one or various layers of intermediate storage units. These layers
contain units that store intermediate information produced by the neural
units, and as such allow us to force the coincidence of the outputs of the
processing units.
5) A set of directed links. They connect input links or intermediate layers to
neural units, and neural units to intermediate or output units.
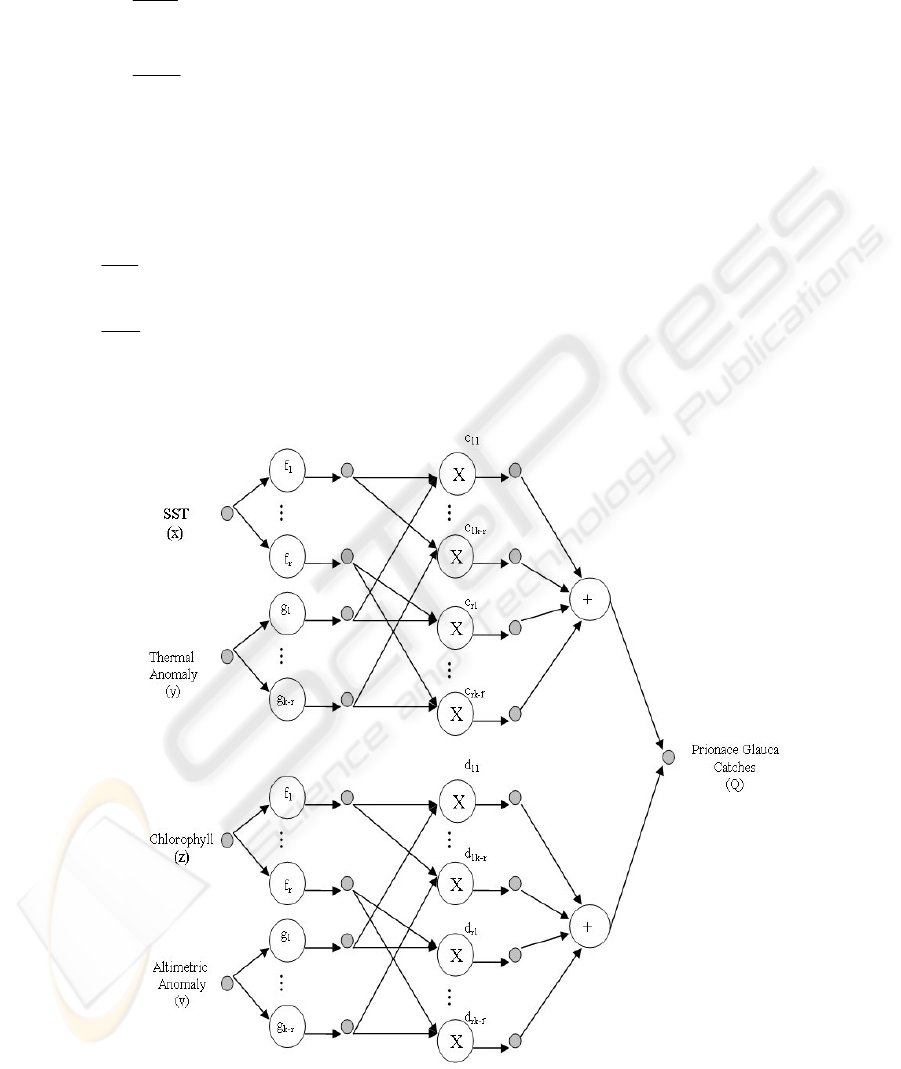
2.2.2.1 Implemented Functional Network
We have adapted the separability model explained in [15] to our problem. The
topology of the proposed network for the prediction of Prionace Glauca catches
appears in Figure 2.
In this model, the two functions families are known: {f
i
| i=1,…,r} and {g
j
|
i=1,…,k-r }, and output Q can be calculated as follows:
∑∑ ∑∑
=
−
==
−
=
+=
r
i
rk
j
r
i
rk
j
jiijjiij
vgzfdygxfcQ
11 11
)()()()(
(1)
We must therefore calculate the adequate coefficients c
ij
and d
ij
, based on the
training set that was already used for the neural networks. The learning process of our
network can be described as follows:
The error e
k
of each pattern is defined as:
∑∑ ∑∑
=
−
==
−
=
+−=−=
r
i
rk
j
r
i
rk
j
kjkiijkjkiijkkk
vgzfdygxfcxQxe
11 11
00
)()()()(
(2)
The final purpose of our training is to minimize the sum of the errors of all the
patterns, i.e., minimize E:
∑
=
=
n
k
k
eE
1
2
where n is the number of patterns of the training set
(3)
According to the method of square minima, the patterns set that minimizes E must
be the solution of the following equations system:
116

⎪
⎪
⎩
⎪
⎪
⎨
⎧
==
∂
∂
==
∂
∂
∑
∑
=
=
n
k
kqkpk
pq
n
k
kqkpk
pq
vgzfe
d
E
ygxfe
c
E
1
1
0)()(2
0)()(2
with p=1,…,r; q=1,…,r-s
(4)
If we replace e
k
by expression (2), we obtain the following equations system:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+=
∂
∂
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+=
∂
∂
∑∑∑ ∑∑
∑∑∑ ∑∑
==
−
==
−
=
==
−
==
−
=
n
k
kqkpk
r
i
rk
j
r
i
rk
j
kjkiijkjkiij
pq
n
k
kqkpk
r
i
rk
j
r
i
rk
j
kjkiijkjkiij
pq
vgzfevgzfdygxfc
d
E
ygxfevgzfdygxfc
c
E
111 11
111 11
0)()()()()()(2
0)()()()()()(2
with p=1,…,r; q=1,…,r-s
(5)
Fig. 2. Functional network based on the proposed separability model for capture prediction.
117

In order to obtain comparable results, we use the same training patterns as those
used to train the neural networks of the previous section. Functional networks are
especially appropriate for problems with mathematical models. In our case, where
there is no model, we opt for the elementary polynomic family to resolve the system.
We have carried out tests with the following functions families:
- Case 1: {f
i
}={1,x,x
2
,x
3
} and {g
i
}={x,x
2
,x
3
,x
4
}.
- Case 2: {f
i
}={1,x,x
2
,x
3
,x
4
} and {g
i
}={x,x
2
,x
3
,x
4
,x
5
}.
- Case 3: {f
i
}={1,x,x
2
,x
3
,x
4
,x
5
} and {g
i
}={x,x
2
,x
3
,x
4
,x
5
,x
6
}.
We must be especially cautious when selecting the functions families, because the
determinant of the coefficients matrix could have two identical columns. This is why
the family {g
i
} does not contain the elemental function “1”.
2.2.3 ANFIS
We have implemented ANFIS type 3 systems (Takagi-Sugeno) [16][17], using the
already used patterns for neural and functional networks as training and validation
sets, and searching the best topology for our system. We have defined various ANFIS
[17] for the different tests, and the best results were obtained by the system that had 2
membership level functions for each variable. The output is of the order 0 (constant
function).
Figure 3 shows the topology:
Fig. 3. Topology of the ANFIS system of case 1, in which for each input variable there are only
two characteristic functions (membership functions, MF).
3 Results
3.1 Comparing results
We have used 4 input variables (SST, Heating-Cooling, chlorophyll concentration,
and altimetry) and one output variable (Quenlla catches) to create a multilayer
perceptron trained with an error Backpropagation algorithm [18] [19].
118

Our purpose was to find the simplest network that allows us to draw conclusions
on the conditions that maximize the catches of the embarked unit. After training the
network, we noticed that the number of neurons of the hidden layer hardly affects the
error presented by the network. There are small initial differences that may be due to
the arbitrary initialization of the network’s weights. In all the cases, the MSE of the
training set remains close to 0.01, whereas the error of the validation set is slightly
below 0.02.
These results point towards the simplest network, i.e. the network with 2 neurons
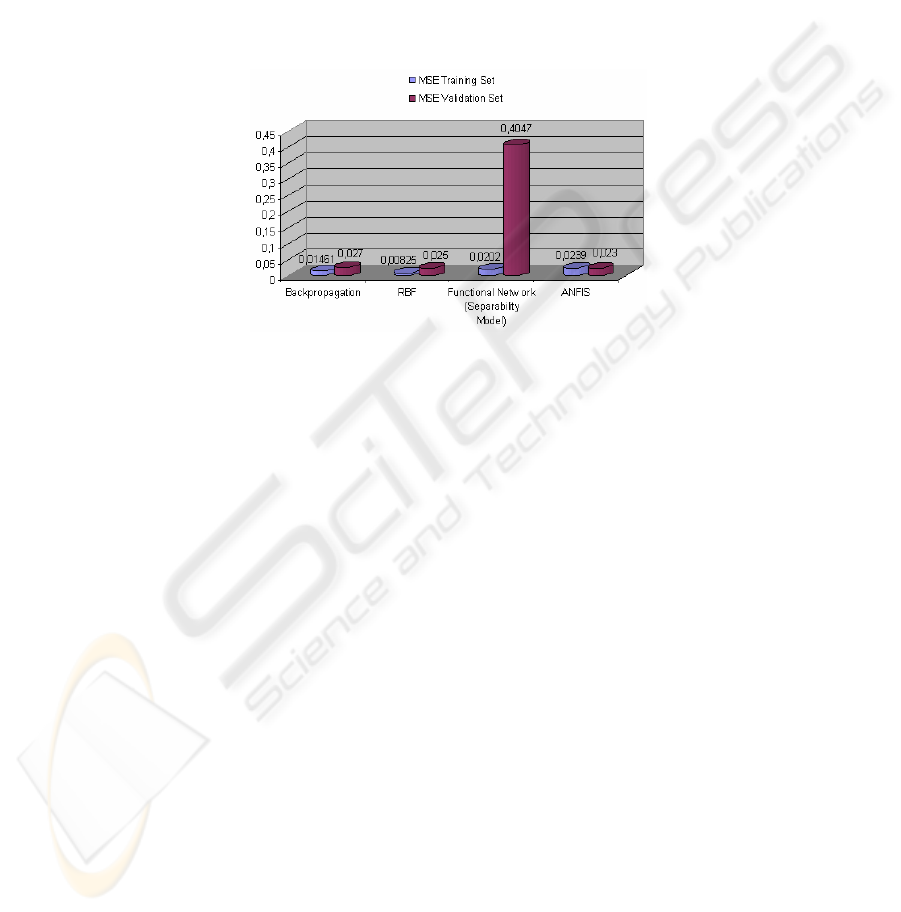
in its hidden layer. Figure 4 shows the mean square errors of the training and
validation set of other modern paradigms in AI, the functional networks [15], and the
neuro-diffuse system ANFIS [17]:
Fig. 4. MSE of the training and validation sets in 4 tested algorithms.
If we want the studied algorithm to be a good predictor, we must obtain a low error
for the training and validation set. We created this validation set with field data that
we are not used during training. This validation set contains a representative number
of all the patron types of the field data. A validation error that is considerably bigger
than a training error indicates a case of over-adjustment or over-training. It is well
known that when we use a model with many parameters to adjust a dataset that
proceeds from a process with a small degree of liberty, the obtained model may not
discover the real tendencies of the original process, even though it may present only a
small data adjustment error. In this case, the training is limited to the interpolation of
the data, including the noise, by means of a complicated sigmoid function.
Figure 4 shows the best results after training the different neural, functional and
ANFIS networks, and avoiding all the cases that presented over-adjustment. The
errors of Figure 4 are all of the same order, except the validation error of the
functional network. This means that the generalization capacity of this algorithm is
smaller for our particular case, due to the inexistence of a mathematical model that is
able to explain the problem [20].
Finally, the system was implemented with the multilayer perceptron trained with a
Backpropagation algorithm, which is simpler than the ANFIS and the RBF network.
The Backpropagation network can now be applied to calculate the probability map
of Prionace Glauca catches. The network inputs are the values of the pixels of each
image; the input that corresponds to the altimetric anomaly is the value (not zero) that
is closest to the pixel, if it does not already exist. We use the network output to
generate a fishing probability map that can be exported to a SIG (see Figure 5). The
high grey levels (clear colours) indicate a high fishing probability.
119

Fig. 5. Probability map of Prionace Glauca catches on 7-8-1998, obtained through a neural
network trained with a Backpropagation algorithm. High grey levels (clear colours) indicate a
high fishing probability
4 Conclusions
9 We have elaborated a decision support system for the operational
exploitation of fisheries by integrating various Artificial Intelligence
techniques into a data acquisition system with data from remote sensors.
9 Based on the images of two entire years (1998 and 1999) and on field data,
we have generated an extensive information system that includes a relational
database with environmental parameters, geographical coordinates and
catches.
9 We have used the previously mentioned information system to design a
decision support system. Our problem is characterised by the absence of
global and local models, the inexistence of a knowledge base, and by
variables that are poorly interrelated (except for the anomalies and the
thermic fronts). These factors have led to the use of algorithms of the
connectionist tendency within the Artificial Intelligence field.
9 We have designed several tools that are able to predict the optimal fishing
grounds according to the information of a series of satellites. The obtained
results were validated with patterns that differ from those that were used for
the training.
9 In order to develop the necessary applications to integrate the neural network
into the digital treatment of images, we had to previously unify the different
image formats for each satellite. The output of the system consists in a
fishing probability map generated from the used network outputs. At the
same time, we have implemented applications to access the information
system and to calculate punctual predictions. These tools were developed in
such a manner that the user of the system disposes of all the utilities in a
comfortable and accessible environment.
120

References
1. Triñanes J. A.. Sistema de información basado en tededetección para ayuda a la explotación
operacional de pesquerías de túnidos y otras especies pelágicas. Tesis doctoral.
Departamento Electrónica e Computación, Universidad de Santiago. (Febrero 1998)
2. Iglesias A. Sistema de apoyo a la explotación operacional de pesquerías basado en técnicas
de inteligencia artificial y teledetección. Departamento de Electrónica y Computación,
Facultad de Física, Universidad de Santiago de Compostela. (Mayo 2003)
3. Cotos J. M. Dinámica y clasificación de estructuras oceánicas para aplicación operacional
de pesquerías utilizando teledetección e ingeniería de conocimiento. Tesis doctoral.
Departamento de Física Aplicada, Facultad de Física, Universidad de Santiago de
Compostela. (Septiembre 1994)
4. Wells W. M. Efficient Synthesis of Gaussian Filters by Cascaded Uniform Filters. IEEE
Trans. Pattern Analysis and Machine Intelligence-9 No. 2 March 1986.
5. Harlow C. A., Trivedi M. M., y Conners R. W. Use of texture operators in segmentation.
Optical Engineering, vol. 25 , no. 11, pp. 1200-1206, Nov. (1986)
6. Komatsu T., Aoki I., Mitani I., y Ishii T. Prediction o the Catch o Japanese Sardine Larvae
in Sagami Bay Using a Neural Network. Fisheries Science 60(4),385-391 (1994).
7. Aurelle D., Lek S., Giraudel J., Berrebi P. Microsatellites and artificial neural networks:
tools for the discrimination between natural and hatchery brown trout (Salmo trutta, L.) in
Atlantic populations. Ecological Modelling 120 313-324. (1999)
8. Dreyfus-Leon M. J. Individual-based modelling of fishermen search behauviour with neural
networks and reinforcement learning. Ecological Modelling 120 287-297. (1999)
9. Aussem A., Hill D..
Neural-network metamodelling for the prediction of Caulerpa taxifolia
development in the Mediterranean sea. Neurocomputing 30 ; 71-78 (2000)
10. Brosse S., Guegan J., Tourenq J., Lek S.. The use of artificial neural network to assess fish
abundance and spacial occupancy in the litoral zone of a mesotropic lake. Ecological
Modelling 120:299-311. (1999)
11. Maas O., Boulanger J., Thiria S. Use of neural networks for predictions using time series:
Illustration with the El Niño Southern oscillation phenomenon”. Neurocomputing 30: 53-
58. (2000)
12. Specht D. F. Probabilistic Neural Networks. Neural Networks, 3,109-118. (1990)
13. Zhang Q. and Benveniste A. Wavelet Neural Networks. IEEE Transactions on Neural
Networks, 3, 889-898.
14. Castillo E. and Gutiérrez J.M. Nonlinear Time Series Modeling and Prediction Using
Functional Networks. Extracting Information Masked by Chaos. Physics Letters A, Vol.
244, 71-84 (1998).
15. Castillo E., Cobo A., Gutiérrez J.M., and Pruneda E. Introduction to Functional Networks
with Applications. A Neural Based Paradigm. Kluwer International Publishers (1999).
16. Takagi T. y Sugeno M.. Derivation of fuzzy control rules from human operator`s control
actions. Proc. Of the IFAC Symp. On Fuzzy Information, Knowledge Representation and
Decision Analysis, pages 55-60. (July 1983)
17. Jang J.-S.R. ANFIS: adaptive-network-based fuzzy inference system. IEEE Trans. Syst.,
Man., Cybern, vol.23, no.5, pp. 665-685. (1993)
18. Gorman R. P. y Sejnowski, T. J. Learned Classification of Sonar Targets Using a Massively
Parallel Network. IEEE Transactions on Acoustics, Speech, and Signal Processing.
36:1135-1140. (1998)
19. Rumelhart D.E., Hinton, G. E. y Williams, R. J. Learning internal representations by errors
propagation. In Parallel distributed processing: Explotations in the microstructure of
cognitron. Vol. 1. D.E. Rumelhart and J.L. Mac Clelland, Cap. 8. MIT Press. (1986)
20. Iglesias A., B. Arcay, J.M. Cotos. Optimisation of fishing predictions by means of Artificial
Neural Networks, ANFIS, Functional Networks and Remote Sensing images. Expert
Systems with Applications. Aceptado y pendiente de publicación.
121