A Hybrid Evolutionary Probablistic Framework for

Developing Robotic Team Behaviors

Edward Newett

and Ashraf Saad

Georgia Institute of Technology, School of Electrical and Computer Engineering

Atlanta, Georgia 30332, USA

Georgia Institute of Technology, School of Electrical and Computer Engineering

Savannah, Georgia 31407, USA

Abstract. One of the inherent issues in team-based multiagent robotics is coordi-

nating a cooperative task decomposition. Use of explicit communication models

or game theoretic approaches to model teammate behaviors can be costly and

error-prone. This paper describes a method of discovering a set of behaviors that

allows a team to intrisically function in a collaborative manner. Probabilistic plan-

ners based on spreading activation networks that determine these behaviors are

implemented in each robot. A genetic algorithm is used to ﬁnd the appropriate

link strengths within each of these networks to produce an overall dynamic team.

It is shown that a team controlled by spreading activation networks can perform

well as a team by maintaining these behaviors in environmental situations other

than the one used for GA evolution. From this framework, a goal-directed task

planning approach can be envisioned to deploy a fully functional robot team.

1 Introduction

Many applications in robotics focus on the design of a single agent capable of solving a

complex problem. However, certain domains may be better suited for a team of robots.

There are several reasons common to various scenarios in which multiple robots may

be better than one [1]. Multiple robots are capable of being in several places at the same

time and can perform distributed action in parallel. A team can coordinate the decom-

position of a problem by effectively breaking it down into multiple subproblems. In a

task like exploration or foraging, multiple robots can learn the environment and explore

more of it in less time than a single robot. Finally, multiple robots can be designed to

be less complex than a single robot given the same task.

One way of producing a cooperative relationship between team members is by as-

signing a speciﬁc goal to each member. This method likely requires an explicit decom-

position of the task the agents are collaborating upon. In some tasks, a team of robots

may not be capable of explicitly communicating this decomposition with one another,

either because of communication issues or due to the complexity of the problem includ-

ing robot interference.

Newett E. and Saad A. (2005).

A Hybrid Evolutionary Probablistic Framework for Developing Robotic Team Behaviors.

In Proceedings of the 1st International Workshop on Multi-Agent Robotic Systems, pages 88-101

DOI: 10.5220/0001196500880101

 SciTePress

It is desirable to show that if each team member instead exhibits a certain behavior

conducive to solving a certain part of a problem, and the entire team consists of be-

haviors that mutually complement each other, then the agents can collectively solve the

problem without being assigned explicit subgoals.

This paper focuses on designing a framework to develop the behaviors of individual

robots that comprise the team by developing a Bayesian network within each robot

that captures the correlation between actions of the robot and the observed state of the

environment. These behaviors are generated through a probabilistic planner within each

robot. The probabilistic planner is implemented as a spreading activation network over

the Bayesian network, such that condition-action-effect success likelihoods are based

on what is known about the current state of the environment. Each planner will have

different link strengths between an action and its relation to an environmental condition,

and the goal is to develop the link strengths of each planner so as to produce an overall

desirable team behavior.

In order to demonstrate this conceptual framework, an experimental simulation test-

bed is built comprising several robots dispersed in a ﬁeld containing a certain number

of light sources. The goal is to locate as many light sources as a possible within a pre-

speciﬁed amount of time. This speciﬁc task is better suited for a team of robots since

the area to be covered can be divided and explored more quickly by the whole team.

The problem of effectively coordinating team behavior involves subproblems such as

minimizing robot interference and overlap of work between robots.

A fundamental issue then arises: how are the link strengths of the spreading ac-

tivation network determined for each robot? The large search space of potential link

values for each robot, and for the team as a whole, makes it prohibitive from a com-

putational standpoint to perform an exhaustive search. Therefore, a search based on

genetic algorithms (GA) is employed. The GA searches for collective action sequences

to produce collective team behaviors that maximize exploration and localization of light

sources. From the evolved team, condition-action vectors experienced during simula-

tion are recorded and used to seed the link strengths between actions and possible effects

within the spreading activation networks. Each team member should experience a dif-

ferent section of the environment for effective decomposition of the task at hand, and

the corresponding condition-action vectors are then captured to yield the desired team

behavior.

2 Background Work

The majority of the spreading activation task planner design is based on a probabilistic

planner developed by a team at Vanderbilt University [2]. A layered control architecture

is designed based on work related to the DAC5 control system [3] used in a similar

foraging task. Many design choices were made when developing this particular multi-

agent system, each with their own tradeoffs [4]. A few of these tradeoffs are identiﬁed

and examined next.

2.1 Team Learning Versus Concurrent Learning

In some cases, team learning refers to an implementation that involves a single, central

learner. On the other hand, in concurrent learning, learning occurs in each robot. In this

case, learning is distributed as tends to be the case in many real environments where

learning takes place online; i.e., while the robots are operating. This case enables robots

to learn separate tasks or subtasks.

In this work, a GA is used where genes comprise the action sequence used by each

robot during simulation. The performance of each robot is evaluated by the ﬁtness func-

tion. The population of genes is broken down so that a separate subpopulation of genes

is dedicated to evolve the action sequence for a given robot.

2.2 Evolving a Team to Solve a Common Problem

Using an evolutionary technique, such as GAs, depends on deﬁning a ﬁtness function.

The task of evolving robots for exploration as opposed to locating an item is primar-

ily speciﬁed in the GA through the ﬁtness function. Once a framework is set up for

multiple agents to learn a speciﬁc task, the desired performance can be altered to an-

other task by changing the ﬁtness function. Given a common ﬁtness function with the

proper constraints, a GA will search for a team that naturally decomposes a problem

into subproblems.

3 Forming Effective Teams: A Hybrid Approach

SUBPOPULAT ION

GA POPULATI ON

TEAM SELECTION

SIMULATION

FITNESS EVALUATION

Store Team Fitness

Store AC Vectors

Retrieve AC vectors

from best team

BUILD PROBABILITIES

INITIALIZE SA NETWORKS

SIMULATION WITH SA

Done?

Yes

Choose Genes

Repeat n time steps

Fig.1. Block diagram of the hybrid approach.

Figure 1 outlines the major steps of the framework designed in this work. Initially, a

genetic algorithm is used to search for collective action sequences that maximize team

performance. This involves repeating the steps of team selection, simulation, and ﬁtness

evaluation until an appropriate team is identiﬁed. The action-condition vectors and team

ﬁtness values are stored for each generation, and following evolution, the vectors which

represent the best evolved team are used to build probabilities (represented by link

strengths) within each spreading activation network.

These link strengths distinguish behaviors among the robots as all other aspects of

the spreading activation networks are identical between robots, along with designer-

speciﬁed goals. Once the spreading activation networks are initialized, each robot is

controlled through a reactive and adaptive layered approach.

3.1 Employing a Genetic Algorithm

Producing good overall team performance depends on determining the link weights

of the spreading activation network for each robot. Given the large search space for

potential values, a GA was chosen as the search mechanism. Although a GA could be

used directly to ﬁnd these link strengths, the approach taken is to use the GA to evolve

the action sequences of the team. Searching for action sequences is likely a more direct

and time efﬁcient search since the genes of the GA consist only of n possible actions.

The link strengths are encoded in the genotypes of the GA using real values ranging

between [-1 and 1]. Therefore, with a small and static set of possible values for each

allele, convergence times could be drastically reduced. To further reduce the search

complexity, genes are divided into subpopulations, with each subpopulation maintained

for a separate robot.

3.2 Using GA Subpopulations

In general, by partioning a population of genes into subpopulations, a variety of new

possibilities emerge. If each individual of a subpopulation is only mated with another

member of the same subpopulation, then the structures between subpopulations can

vary. This gives rise to different species of genes and allows for a simple way to keep

track of which individuals can pair with which others during crossover. Other methods

of maintaining species include assigning an innovation number [5], which would allow

for multiple species to coexist within a subpopulation. Subpopulations are mainly used

in this experiment to allow each robot to develop a different behavior and to allow the

decomposition of the problem. Each robot is assigned a speciﬁc subpopulation through-

out the evolution process. In this way, the subpopulations for each robot may converge

towards different subgoals, resulting in the desired implicit task decomposition. Within

each subpopulation, individuals are assigned ﬁtness values based on performance dur-

ing simulations. Additionally, a team ﬁtness value is maintained for every group of

individuals used together in each simulation run. This team ﬁtness value is used to pro-

duce cooperative behavior: a combination of individuals that perform well together by

exhibiting task decomposition is given a higher team ﬁtness value.

3.3 Spreading Activation Networks

A spreading activation network as used in this work is a connectionist type network in

which layers of nodes represent either possible actions or possible states of the envi-

ronment as perceived via the robot sensors. Spreading activation is attractive because

it allows for efﬁcient search potentially in parallel and in a fashion that happens to be

analogous to human information processing [6].

The behaviors of team members are determined by the weights of links that connect

layers of the spreading activation networks. Figure 4 shows a portion of a spreading

activation network such as those used in the experiments. The weights between pre-

conditions (the value of conditions observable in the current state of the environment)

and actions, as well as between actions and post-conditions (in the next state) can be

deﬁned differently for each member of the team. These weights determine how each

robot will make decisions: if the resulting probability of a certain action sequence being

successful in bringing a robot to a goal condition is higher for one robot, it may perform

this sequence where another robot in the same state would not.

3.4 Probabilistic Task Planning

Goal-oriented planning techniques are utilized that involve back propagation of goal

utilities, forward propagation of condition utilities, and action selection as previously

developed in [2]. In particular, when the adaptive control layer is active (indicating

no direct rewards), planning is performed until one of the actions in the current state

accumulates enough utility and is selected. Action utilities are typically compared to a

threshold value, and when an action exceeds this threshold, it is selected.

Figure 4 shows a portion of the spreading activation network. The ﬁrst layer consists

of conditions observed in the environment, or the preconditions present before acting.

These preconditions are linked to possible actions the robot may perform, and the con-

nections indicate the likelihood of an action succeeding given the state. These links,

denoted w

, are determined by the following equations [2]:

(

> 0 if (c

= T) increases P(a

success

)

< 0 if (c

= T) decreases P(a

success

)

(1)

where T indicates a true condition and F a false condition. The link strength w

between an action a

and one of its effect propositions c

is deﬁned as follows:

(

P (c

= T|a

exec

) if a

sets (c

= T)

−P (c

= F|a

exec

) if a

sets (c

= F)

(2)

During backpropagation, action utilities are then updated to determine the best ac-

tion to take. First goal utilities U(c

) are examined:

U(c

) =











> 0 if (c

= T) ∈ G

< 0 if (c

= F) ∈ G

= 0 if c

/∈ G

(3)

Then the utility of condition c

is combined with the probability of the condition

existing in the current state of the environment and action-effect link strengths to deter-

mine the reward of performing an action a

R(a

) =

(

P (c

= F|S

)U(c

) if(w

> 0)

P (c

= T|S

)U(c

) if(w

< 0)

(4)

These action rewards are summed over all conditions deﬁning the action utility for

action a

U(a

) = −C(a

) +

P (a

success

)R(a

) (5)

3.5 Extracting Action-Condition Vectors

The action sequences that represent the best team are extracted from the GA and paired

with the condition vectors recorded during the simulation of that team. For every action

in the sequence, the condition vector contains the corresponding environmental condi-

tions present. The link strengths between actions and effects of the spreading activation

networks are seeded with these action-condition pairs by evaluating the distribution of

conditions that occured after every action. A link strength w

is then determined by

the frequency of an effect proposition being true after an action was executed over n

simulation steps:

(

+1 if (c

= true|a

exec

)

−1 if (c

= false|a

exec

)

(6)

Frequency is incremented for every condition c

that is true after action a

is ex-

ecuted. If c

is false after action a

is executed, the frenquency count is decremented.

This method effectively correlates actions with effects as they tend to appear in the ob-

served environment. If an action a

results in equally frequent occurrences of c

being

true and false, w

will accumulate to zero, indicating no relationship.

3.6 Switching Between Reactive Control and Planning

WORLD

Actuators

Sensors

Goal conditions

Layer

Selection

Fig.2. Block diagram of the control system. The reac-

tive layer is activated whenever the sensors return val-

ues that pass a threshold and indicate a goal condition.

Reactive control takes over

Fig.3. A scenario demonstrating a

switch between adaptive and reac-

tive control.

To improve individual performance, a distributed control model was then developed

which incorporates a two-layered approach: a reactive control layer is used in situations

where a sensor stimuli indicates a direct reward (either positive or negative), and an

adaptive control layer is used where no direct reward is observable from the sensors

thus requiring planning (see Figure 2). The reactive control layer equips the robot with

minimal behavioral competence to deal with its environment and is only active when

a target (light source) or collision condition are certain to occur if the robot does not

react. Figure 3 shows an example of a robot that is exploring towards the north-east

while a wall is sensed on the right. Also shown is how the reactive control layer takes

over as soon as a direct reward is observable (here the light sensors have discovered a

light source and the robot turns towards it). The amount of planning at any time during

execution varies depending on how many action-condition steps need to be evaluated to

achieve a high enough action utility for an action at the current step, which is discussed

further in section 4.

4 Implementation

A Khepera robot simulator is used in this work as described below. The task given is

to localize as many light sources as possible in a prespeciﬁed amount of time, which

should be solved best by a team that works together by dividing up the map between

robots to cover the largest possible area. Initially, action sequences are evolved to ﬁnd

an optimal team as deﬁned by the set of action sequences. Then, control is transferred

to spreading activation networks and performance is qualitatively evaluated.

Three types of sensors are incorporated into the conditions layer of the spreading

activation network: 8 light sensors, 8 distance sensors, and a compass. Each of these

types is divided so as to produce four Boolean conditions for each type. For the light and

distance sensors, threshold values are used to specify whether a wall (light) is detected

directly in front, to the left, to the right, or behind the robot. The compass is used

to record roughly which of the eight cardinal directions the robot is facing. Figure 4

indicates these conditions in the preconditions and effects layers of the network.

Go_Forward

Turn_Left

Turn_Right

Wall_Forward

Wall_Left

Wall_Right

Wall_Behind

Facing_North

Facing_East

Current State

Wall_Forward

Wall_Left

Wall_Right

Wall_Behind

Facing_North

Facing_East

Next State

Wij

Wjk

Fig.4. Portion of the spreading activation network.

The actions a robot may perform are limited to forward movement, turning left, or

turning right. An action period is deﬁned so that the robot does not attempt to plan at

each time step (since very little would have changed in the environment). Between each

action period, the robot examines its current state received from the sensors, and if no

direct reward is in the state it will plan. Once a decision is made, an action is performed

for action period time steps, and the sensors are examined for direct rewards and other-

wise planning begins again. This allows the robot to choose the optimal decision based

on known probabilities at each action period.

4.1 Simulator

The experiment makes use of a freely available Khepera simulator written in C [7].

The simulator evolved into a higher level and more general program called Webots (not

a freeware) that allows for more sophisticated simulations on a number of robots and

platforms.

An alternative Khepera simulator, KiKS [8], was also considered. KiKS is Matlab-

based and provides a smoother interface and multiple robot support via a network

client/server implementation. However, for the purpose of implementing GAs, this sim-

ulator may be less suitable. The fastest simulation run of a single robot that was achieved

with visualization turned off was 2000% the speed of the Khepera being simulated, with

a simulation of 200 steps taking a matter of seconds. Since a typical GA evolution can

involve thousands of simulation runs, this severely impacts the degree to which the net-

works could be feasibly evolved. Additionally, since multi robot support is currently

network-based, evolution of multiple robots seems even less suited to this simulator.

The lightweight C simulator can be run orders of magnitude faster than KiKS, and this

ultimately led to selecting it as the simulator for the experiments we conducted.

Fig.5. The C-based Khepera simulator and

environment used. The team of three robots

begin in the lefthand section of the map.

Table 1. Parameters for genetic algorithm

Parameter Value

Gene size (action sequence length) 140

Subpopulation size 7

Number of subpopulations 3

Max generations 30

Elitist genes per generation 1

Crossover rate 0.9

Mutation rate 0.05

4.2 The Evolutionary Process

The GA was implemented with parameters as shown in Table 1. One subpopulation is

assigned permanently to each robot, which consists of 7 action sequence genes. Initially,

all gene alleles are assigned one of three action values: FORWARD, TURN

LEFT,

and TURN

RIGHT are the possibilities with FORWARD being 80% as likely as the

other two. At each stage of evolution the genes are evaluated, and the gene with the

highest ﬁtness value is ﬂagged as the ’best’ of the subpopulation. These best genes are

copied directly to the next generation. This method of elitism ensures that individuals

with very high ﬁtness are not lost through further evolution. The rest of the genes are

then sequentially processed. For each gene, there is a 5% chance of mutation, and if

mutation takes place then 5% of the gene is assigned a random action. If the gene is not

mutated, then it undergoes crossover with a random individual from the subpopulation.

Crossover takes place uniformly at one random point where the action sequence values

are swapped between the two individuals.

4.3 Evaluating Fitness

The map on which the experiment took place has dimensions 1000.0 by 1000.0 and is

shown in Figure 5. The map was partioned into 100x100 equal sized sections. During

a simulated run, the path of each robot is tracked, and the number of sections traversed

is tallied. Along with this exploration ﬁtness, the number of light sources each robot

encounters is recorded. The ﬁtness function assigned to each action sequence gene is as

follows:

= s

+ (500l

) (7)

F (n) =

i∈n

+ 100l

) (8)

where in (7), s

indicates the number of unique sections of the map member i explored

and l

refers to the number of different light sources discovered with this action se-

quence. The ﬁtness function assesses a combination of the team and individual ﬁtnesses.

A majority of weight is placed on individual ﬁtness, but members are also rewarded for

working well with others: the team members in the combination set n in (8) the ﬁt-

ness values from (7) are summed, and extra reward is assigned for the number of light

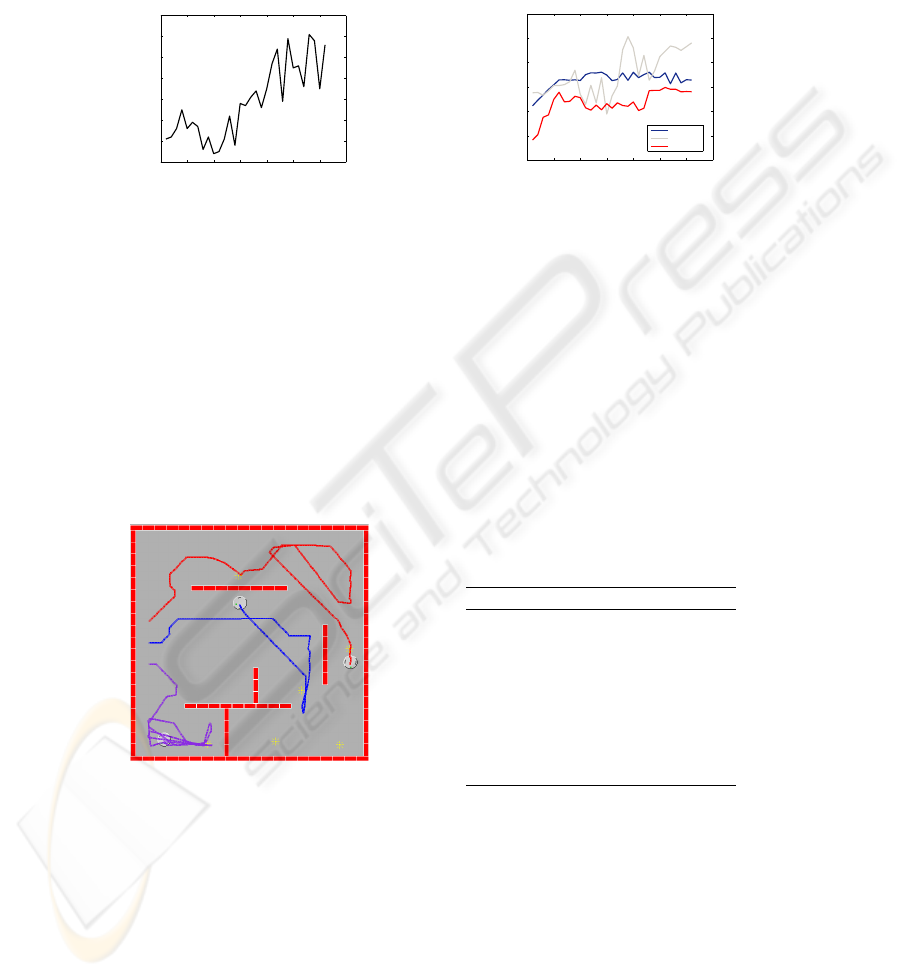
sources the entire team discovered. Figure 6 shows the typical performance results of

the GA in a plot of best team ﬁtnesses achieved over 30 generations. Figure 7 shows the

average ﬁtnesses of each subpopulation along with the ﬁtnesses of the best members.

A typical resulting best team performance simulation is shown in Figure 8. In this

simulation, each of the three robots explores a separate major section of the map. Each

of the three robots begins in the same initial position each simulation run with all three

robots in the center of the board side by side. Every member of every subpopulation

is run against every member of every other subpopulation. This increases the search

space signiﬁcantly, which is one of the reasons a smal subpopulation size and only

three robots were used. At the end of each run, the genes are assigned individual ﬁtness

values and the team of genes is given a team ﬁtness value.

0 5 10 15 20 25 30 35

890

900

910

920

930

940

950

960

Generation

Team fitness

Fig.6. Best team ﬁtness values over genera-

tions.

0 5 10 15 20 25 30 35

2.5

3.5

4.5

x 10

Generation

Fitness

Population 1

Population 2

Population 3

Fig.7. Individual Fitness values of best mem-

bers of each generation.

Fig.8. Paths of an evolved team. Each mem-

ber of the team explores a separate section of

the map.

Table 2. Rewards for Environmental Goal

Conditions

Goal Condition Reward Value

Wall in front of robot -10

Wall left of robot 5

Wall right of robot 5

Wall behind robot 10

Light in front of robot 30

Light left of robot 20

Light right of robot 20

Light behind robot 20

4.4 Simulating Team Behaviors

The spreading activation networks are then initialized. Each network consists of three

layers. The preconditions layer is initialized with propositions as observed in the cur-

rent state of the environment. The effect (or postconditional) layer consists of reward

values for each condition being present in the goal state, which then determine action

utility as in (3). Table 2 shows the reward values assigned to each condition. A negative

reward implies that the condition is undesirable, which is the case with a wall in front

of the robot. With negative rewards, the robot will plan against adverse environmental

conditions: for instance, if it is likely that a wall will be observable in front of the robot

after performing an action, that action’s utility is lessened. Also, by assigning positive

rewards to having a wall on the left or right of the robot (as is the case in Table 2) will

result in a wall following behavior.

Table 2 does not include rewards given for each speciﬁc orientation. Assigning a

higher reward to facing north and east, for instance, would result in robots that tend

to explore towards the northeast. However, since these rewards are common to all ro-

bots, it is undesirable to hardcode behaviors in this way. Instead, the link strengths

between these orientation conditions and each action, which are unique for each robot,

will provide these behaviors. These orientation reward values must be balanced with

other utilities, such as wall conditions, otherwise the robot may prefer to face a wall as

long as it is oriented in the preferred direction. Also, these orientation rewards should

not be hardcoded to zero, or robots will be unable to develop behaviors based on these

conditions.

In selecting actions there is often the possibility that no action seems desirable, or

all actions seem equally desirable. In these situations the robot may continue planning

indeﬁnitely. To keep this from occuring, the forward propagation lookahead is limited to

a value assigned at design time. The value chosen for the experiments was 4 lookahead

states. In the case that no conditions are present in the environment to make any of the

possible actions desirable (i.e. all action utilities are zero), the default action is to move

forward. This is rarely needed when the orientation conditions can themselves cause an

action to be desirable, which is further discussed in the next section.

4.5 Applying Evolved Team Actions to Spreading Activation

Next, the action sequences and corresponding condition vectors of the best team simu-

lation run from the GA evolution are used to initialize the link strengths of the spreading

activation networks. A portion of these link strengths are shown in Figure 9. Since these

link strengths are limited directly to the experience of the particular run corresponding

to the GA simulation, they are heavily biased to that particular run and are not guaran-

teed to necessarily represent the environment accurately. However, the biasing results in

each robot exhibiting a different behavior based on how they perceive the environment.

It is through this biasing that behaviors are developed.

Figure 10 shows a resulting simulation of 2000 time steps, or equivalently twice the

length of action sequences used in the GA simulations. Heterogeneous robot behaviors

are apparent from the ﬁgure. The path of robot #2, indicated in blue, is the least produc-

tive, but exhibits wall-following around the perimeter of the map. Robot 1, with a path

Go_Forward

Turn_Left

Turn_Right

Wall_Forward

Wall_Left

Next State

Robot # Link Strength

1 Forward->Wall_Forward 0.74

1 Forward->Wall_Left 0.68

1 Turn_Left->Wall_Forward 0.08

1 Turn_Left->Wall_Left 0.10

2 Forward->Wall_Forward 0.64

2 Forward->Wall_Left 0.05

2 Turn_Left->Wall_Forward 0.48

2 Turn_Left->Wall_Left 0.05

3 Forward->Wall_Forward 0.68

3 Forward->Wall_Left 0.10

3 Turn_Left->Wall_Forward 0.48

3 Turn_Left->Wall_Left 0.06

Fig.9. A portion of the link strengths in resulting spreading activation networks. Link strengths

for turning left if there is a wall forward vary: Robot 1 would turn left and Robot 2 would turn

right.

indicated in red, discovers the most light sources by exhibiting a wall-adverse behavior.

The third robot, path indicated in purple, makes its way into the corner but becomes

trapped near that light source.

In Figure 10 it also indicated at what points the robots are being controlled by the

spreading activation networks (adaptive control) and when they are being controlled by

the reactive control layer. When a light source becomes observable by the sensors, the

robot reﬂexively turns towards it. If the IR distance sensors detect a wall in front-left

or front-right of the robot, the robot will turn reﬂexively in the direction opposite to the

wall to avoid a collision.

Figure 11 demonstrates a second simulation result. This time the robots were started

in a different area of the map than where they were trained through the GA simulations.

The results are consistent with those as shown in 10: Robot 2 (blue) exhibits wall-

following, robot 1 (red) exhibits wall-adverseness, and robot 3 (purple) stays around

light sources. The consistency of behaviors conﬁrm that the spreading activation net-

works are controlling the actions of the robots for the majority of the time.

5 Discussion

The results from the simulation indicate that behaviors can be successfully deﬁned by

link strengths within spreading activation networks, and this is a successful framework

for developing such behaviors. These behaviors are more robust than the action se-

quences evolved by the GA, since the robots can be initialized in different areas (or

different maps) and their performance will remain about the same.

It should be noted that the robots did not perform as well as teams when controlled

by the spreading activation networks as compared to the evolved GA sequences, but

some task decomposition was still present. By exhibiting different behavioral roles,

like wall-following versus wall-adverseness, a team of mobile robots is able to explore

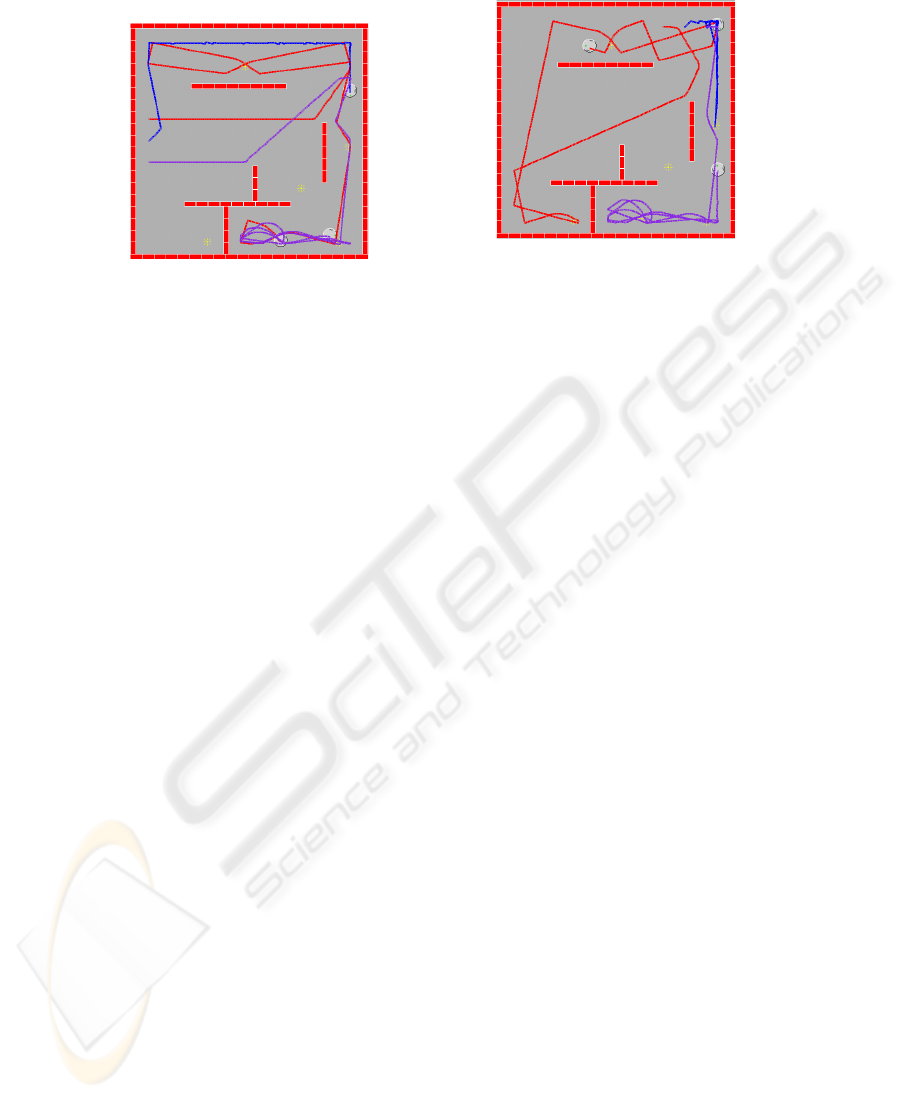
Fig.10. Paths achieved in the same environ-

ment by a team controlled by spreading acti-

vation networks and reactive control.

Fig.11. Paths achieved by starting the robots

in another part of the environment using the

same network link strengths.

more features of any environment. This environmental independence is probably the

most useful result of this experiment.

Reactive control was introduced into the framework design for the purposes of

speeding up GA evolution. Without reactive control, the action sequences produced

would often result in robots running against walls for time segments and hindered over-

all progress. Reactive control, however, adds a bit of additional uncertainty into the

design of action sequences. Robots may be reacting to a wall or to another robot in the

same way. This is ultimately a sensory issue and remains to be addressed.

The GA succeeded in this experiment in decomposing the task of maximizing ex-

ploration between members of the team. Since the problem of optimizing cooperative

team search behavior appears to be NP-hard, it was well suited for a GA search. By

tweaking the actual ﬁtness functions (7) and (8) this decomposition could be manipu-

lated. After most evolutions achieved during the simulations, there was one robot which

evolved better than the others. This robot may have in a way hindered the evolution of

other robots when team ﬁtness was evaluated. Since this action sequence achieved a

high ﬁtness value, it was not as imperative that the other action sequences present in

this particular simulation be as ﬁt in order to survive. By adjusting the team and indi-

vidual ﬁtness functions appropriately, convergence of best team ﬁtness values should

be possible.

The idea behind mapping the action-condition vectors to link strengths of spread-

ing activation networks can be compared to other behavior-based techniques. It is be-

lieved that deﬁning these link strengths based on the performance of only one simula-

tion may not have provided adequate information for creating a robust decision-making

framework. One way of remedying this problem is to increase the length of the ac-

tion sequences that make up the GA genes but with the cost of greater computation

time in performing evolution. Another way would be to evolve the genes until each

subpopulation converges to almost the same action sequences. Then, using all of the

genes from each subpopulation in creating link strengths of the spreading activation

networks would provide more of an aggregated representation of the appropriate action

sequences.

The framework developed to this point only addresses the ﬁrst portion of what

would be required to deploy a team of goal-directed robots. The latter portion requires

supplementing this framework with a full, goal-directed task planner. This addition to

the framework would need to incorporate a memory system augmented in each robot

to allow task and environment tracking. The behaviors that the robots have developed

would still dominate decision making, but decisions on where to explore next would

also be more inﬂuenced by where the robot has already been.

6 Conclusions

Spreading activation is an effective means of deﬁning planning behavior for a team of

robots. Once the spreading activation networks have been initialized, the robots will ex-

hibit these behaviors independent of their place in the environment or the environment

itself. However, the method of using GA evolution to ﬁnd link strengths for the spread-

ing activation network of each robot requires some centralized method of evaluating

team ﬁtness.

References

1. Arkin, R., Balch, T.: Cooperative multiagent robotic systems (1998)

2. Bagchi, S., Biswas, G., Kawamura, K.: Task planning under uncertainty using a spreading

activation network. IEEE Transactions on Systems, Man, and Cybernetics, Part A 30 (2000)

639–650

3. Verschure, P.F.M.J., Althaus, P.: A real-world rational agent: unifying old and new ai. Cogni-

tive Science 27 (2003) 561–590

4. Panait, L., Luke, S.: Cooperative multi-agent learning: The state of the art. Technical Re-

port GMU-CS-TR-2003-1, Department of Computer Science, George Mason University, 4400

University Drive MS 4A5, Fairfax, VA 22030-4444 USA (2003)

5. Stanley, K.O., Miikkulainen, R.: Evolving neural network through augmenting topologies.

Evolutionary Computation 10 (2002) 99–127

6. Kortenkamp, D., Chown, E.: A directional spreading activation network for mobile robot

navigation. In: Proceedings of the second international conference on From animals to animats

2 : simulation of adaptive behavior, Cambridge, MA, USA, MIT Press (1993) 218–224

7. Michel, O.: Khepera Simulator version 2.0. User Manual. (1996) Originally downloaded from

http://www.i3s.unice.fr/.

8. Nilsson, T.: Kiks is a khepera simulator. Master’s thesis, Ume University (2001)