Cooperative Task Scheduling Among Time-Bounded

Agents

Habiba Belleili

, Maroua Bouzid

and Mokhtar Sellami

LRI Laboratory

Badji Mokhtar University

BP 12 Annaba Algeria

GREYC-CNRS

BD Maréchal Juin BP 5186

Badji Mokhtar University

14032 Caen Cedex

Abstract. The paper describes an approach to the cooperative execution of

tasks that can benefit from the application of multiple methods. Agents have al-

ternative methods for task solving, ranging from approximate ones to others

that are more precise but also more resource (time) demanding. Tasks have

temporal constraints (deadlines). Agents are resource-limited and operate under

time constraints. Agents go into a negotiation process in order to choose a com-

bination of methods which maximizes the utility of the result. Agents (with

their chosen methods) will be used in sequential levels to progressively improve

the quality of a task solution.

1 Introduction

Resource Bounded reasoning are strategies that handle situation were the optimal

behavior are computationally or economically out of reach. These strategies can

trade-off between the solution quality and the computational resources rather than to

compute an optimal solution. Currently, the most popular forms of resources bounded

reasoning are progressive reasoning [2] [3], anytime algorithms (Dean and Boddy,

1988; Zilberstein and Russel 1996) and multiple methods [1], where centralized con-

trols were proposed.

The motivation of Progressive reasoning is to adapt the quality of the solution to the

available time. It is based on a multilevel technique, which convert an approximate

solution to a more precise one. An important propriety of progressive reasoning is a

decrease improvement of the quality. Effectively, the improvement done at level i is

greater than the improvement done at level i-1. A level can be skipped if its execution

leads to a non-respect of response time of the task.

Multiple methods also known as design-to-time is an approach to real time problem

solving in situation where multiple methods exist for many tasks that the system need

to solve. Design-to-time involves designing solution to a problem that uses all avail-

able resources to maximize the solution quality within the available time.

Bouzid M., Belleili H. and Sellami M. (2005).

Cooperative Task Scheduling Among Time-Bounded Agents.

In Proceedings of the 1st International Workshop on Multi-Agent Robotic Systems, pages 189-197

DOI: 10.5220/0001197601890197

 SciTePress

Our proposition is the combination of these two approaches in a multi-agents archi-

tecture to respond to hard temporal constraints tasks. Task execution is distributed

among hierarchical agent. The hierarchy represents different level of details of task

solution. Furthermore, each agent is equipped with alternative methods that make

trade-offs solution quality versus time. Agents have to coalesce for task scheduling to

maximize the quality of task response with respect to its deadline.

Agents operating in open and dynamic environments must be able to address dead-

lines and resources limitation in their problem solving. In open environments, re-

quests for service can arrive at any time, thus making it difficult to fully plan and pre-

dict the agent’s future workload. In real applications, deadlines or other time con-

straints are present on the agent’s problem solving [1] [4]. Resource limitations may

also stem from agents having multiples tasks to perform and having bounded re-

sources in which to perform them. Furthermore agents require mutual temporal in-

formation so that they can plan downstream from the interaction.

We address in this paper a cooperative task scheduling. The coordination is anytime:

it finds quickly an approximate solution named minimal solution and refines it incre-

mentally while the maximum time allocated to the negotiation allows it. There is no

central control. This approach is suited to problems that require the result to be ex-

pressed at varying levels of details. An application of our application is a flexible in-

formation retrieval system (Zilberstein and Mouaddib, 1997).

The rest of the paper is organized as follow: we start, in section 2, by presenting the

architecture of our system. In section 3 we present the problem and the methodology

we propose. Section 4 the algorithm illustrating the methodology. In section 5, we

analyse our proposition. We finish in section 6 by a conclusion and perspectives of

our work.

2 System architecture

The system is composed of a set of agents, let Gamma=

{

}

,...,, 21 be this set.

Agents will treat arriving tasks progressively in order to improve its solution quality.

Hence agents are organized in levels, which aim the progressive treatment of tasks,

which allows the maximization of response utility.

Each agent

(except for agent of the first level “i=1”and the agent of the last level

“i=n”) has two direct neighbours by default: the low level neighbour

1−i

and the up

level neighbour

1+i

Indirect neighbour agents of low level of agent

are

(1≤ k <i-1). Indirect agents

of up level of agent

are k

(i+1< k ≤ n). In a coalition C for the treatment of a spe-

cific task an agent

has a unique low level neighbour agent from which it get an

entry, and a unique up level neighbour agent to which it communicates results.

Each agent of Gamma has a set of alternative methods for the improvement of task

solution quality. Let

{}

iii

MMM

ααα

,....,,

be the set of alternative methods of

agent

Two alternative methods

and

1−i

, of the same agent

, applied on an entry

of quality q will give two responses with different quality

and

1' −i

. These same

methods will necessitate different times

and

−i

where

1' −i

and

−i

The use of rough approximation by one method negatively affects the performance of

a method that uses its result.

Each agent maintains the distribution of probability of every local technique. The

duration of a local technique of an agent depends on first the local technique used by

low-level neighbour agent and second, on which agent has communicated the entry.

Table 1 shows an example. These estimations are obtained empirically.

Table 1. Example of agent acquaintance: the method 1 of agent i

takes 20 unit of time with

the probability of 0.6 and 30 unit of time with the probability of 0.4 when entries come from

agent

1−i

. This same method takes 60 units of time with the probability of 0.7 and 75 units of

time with the probability of 0.3 when entries come from agent

2−i

…

1−i

2−i

…

Pr Dur Pr Dur Pr Dur

0.6 20 0.7 60 0.75 120

0.4 30 0.3 75 0.2 140

0.7 35

0.3 40

…

0.6 53

0.4 60

3 Methodology outline

The aim is to find, for an arriving task, among agents the ones which compromise the

deadline of the task and hence, will be discarded and for other agents which methods

will be used so that to maximize solution quality of the task. To decide which method

to use for the treatment of a given task, an agent cannot do it individually, because, in

one side, the strategy is global, and in the other side, no agent knows the temporal

constraints of other agents. From this fact, agents must decide together by entering in

negotiation cycles. These later will allow agents to opt for a combination of methods,

which increases (as better as possible) the utility of the response. The utility of the

response to the task is zero if the response is produced after its deadline.

For hard temporal constraints task, the time allocated to the schedule must be limited

in advance otherwise agents will constantly schedule and not perform their commit-

ments.

We want an anytime task scheduling which has always a response at a hand when

interrupted (because of expiration of the maximum time allocated to the schedule). To

guaranty such behaviour we propose two-steps scheduling: the first step finds a

minimal solution, which concerns only the more approximated methods of each agent

of the set Gamma. This will reduce the search area of methods and hence minimize

the search time.

After this, and in second time, agents try to improve, incrementally, the minimal solu-

tion by changing all or part of approximate methods with more precise ones. This

process finishes when the maximal time allocated to the schedule process is expired

or when more improvement leads to the violation of task deadline. The aim is to have

always a solution at a hand under time pressure.

4 Preliminaries Definitions

4.1 Coalition Cost

The cost of a coalition for a task Wj is the necessary computational resource to re-

spond to the task Wj. The cost of a coalition varies with respect to the resource-

consumption by previously formed coalitions for already arriving tasks not yet exe-

cuted. The cost of coalition allows verifying whether or no there is task deadline vio-

lation.

4.2 Utility Function

We define an utility function of an agent i

to a task Wj by

(

)

tWg ji ,

. It is corre-

sponding to the utility to respond to a task Wj at a time t by an agent

. It represents

the inverse of the time window between the expected time the task is ready to receive

improvement by the agent

and the expected time the agent i

delivers its response

to the task Wj.

4.3 Agents Interaction

Agents communicate via a communication protocol, which is based on two primi-

tives: Send/Receive(Sender,Receiver,<Message>).

There are three types of messages:

Invitation-to-participate message: this type of message is an invitation of the sender

to the receiver to look at the possibility to participate for the treatment of the task Wj.

This message vehicles temporal information such the cost of the coalition

Ccomp{Coalition} formed until the sender, the expected time the sender delivers its

result for the task Wj the value of the minimal utility, Umin, until the sender, the

agent which owns the minimal utility arg( Umin) and task identification Wj

Invitation-to-Opt-out message: this type of message is an invitation of the sender to

the receiver to opt out because of its minimal utility until now. The parameter of this

message is task identification.

NewNeighbor message: this type of message is an updating message which permits to

the receiver to know its new up level neighbour after the sender has opted out. Pa-

rameters of this message are: new neighbour identification and task identification.

NoNeighborUp message: only the agent of the last level sends this type of message

when it must opt out due to its minimal utility. The parameter of this message is task

identification. The receiver of this message deduces that it has no neighbour up for the

treatment of the task referenced in the message and that it is the last agent in the coali-

tion formed for the treatment of the referenced task.

5 The algorithm

In this section, we present the two steps of cooperative task scheduling:

5.1 Step I: the minimal solution

In this step agents try to evaluate together the cost of the coalition so that there is no

violation.

Agents reason about their temporal constraints using worst-case performance of their

planned methods. We distinguish two main situations: the first is the design of the

coalition by estimating its cost; the second concerns the detection of a violation of

task deadline. Hence, one agent must opt out. We adopt a utility driven selection,

where agent with the more little utility is invited to opt out from the current negotia-

tion and hence from the treatment of the task. We address in the following these two

situations.

Forward coalition formation for the minimal solution:

When a new task Wj asks for service, agent of the first level initiates the search of the

minimal solution. It estimates its contribution with respect to its workload corre-

sponding to resources consumption by previous commitments, and predicts the time

End-Time(

,Wj) at which it delivers its part of Wj solution by using worst-case per-

formance of its more approximated method Wj and worst-case performance of already

planned methods for waiting tasks (during passed task scheduling). Also it estimates

the cost of the coalition {

} Ccomp{ 1

}for the task Wj. This information will be

communicated to its neighbor of up level by default using an invitation to participate

message:

Invitation-to- participate (

Sender: 1

Receiver:

Temporal information: Ccomp{ 1

},ET( 1

,Wj),

Umin:

∞ ,

Arg(Unim):

Task identification: Wj

);

The utility of agent 1

is always equal to

∞

for its mandatory role.

Each agent of the intermediate level

receives from an agent of low-level temporal

information from which it expects its proper response time for Wj (End-Time(

,Wj))

using worst case performance of its more approximated method for Wj and worst-case

performance of already planned methods for waiting tasks (during passed task sched-

uling). It updates the cost of the new coalition by adding its temporal constraints to

the cost received. Also it estimates its utility for the task Wj, compares it to the one

received and updates the value of the minimal utility and its owner, if necessary. If the

new cost of the coalition doesn’t violate task deadline, it saves locally all expected

temporal information and sends them to the next agent in the hierarchy (if exists).

This process is iterated until agent

and the coalition is progressively formed.

Expectation of task deadline violation

When at a level of an agent i

a violation of task deadline is expected (the expected

coalition cost violates the deadline of the task Wj), agent

has to identify among

agents of low level the agent with minimal utility for the treatment of the new task.

Recall this information is available in the invitation-to-participate message.

When informed (by an invitation-to-opt-out message), the agent with minimal utility

minu

cooperates, for coherent behavior of the schedule, by linking its current low-

level neighbor for the referenced task with its current neighbor of up-level by sending

an updating message. Only at this time the agent with minimal utility

minu

opts out.

The agent receiving the updating about its new neighbor of up-level for the referenced

task has to resume the process of the coalition formation by sending its temporal con-

straints, saved for such event, to its new up-level neighbor agent for the referenced

task. This later must re-estimate its temporal constraints with respect to those re-

ceived: End-Time, coalition cost and the identity of low level neighbor (the sender).

The figure 1 presents the minimal solution principal.

At the end of the first step each agent maintained for the treatment of the new task

must know its neighbors (up and low levels) the expected Ready Time of the task

results (for more improvement) at its level and the expect time it delivers its results

(End Time) for the task to its neighbor of up level, if exists.

5.2 Step II: Improvement of Minimal Solution

In the second step the aim is the improvement of the minimal solution. We distinguish

more then one collective behaviours depending on the cost of the coalition reached in

the first step and the remaining time of the negotiation. We have to fix thresholds un-

der which there is no need to improve the minimal solution (no sufficient time nego-

tiation or the cost of coalition meets approximately the task deadline).

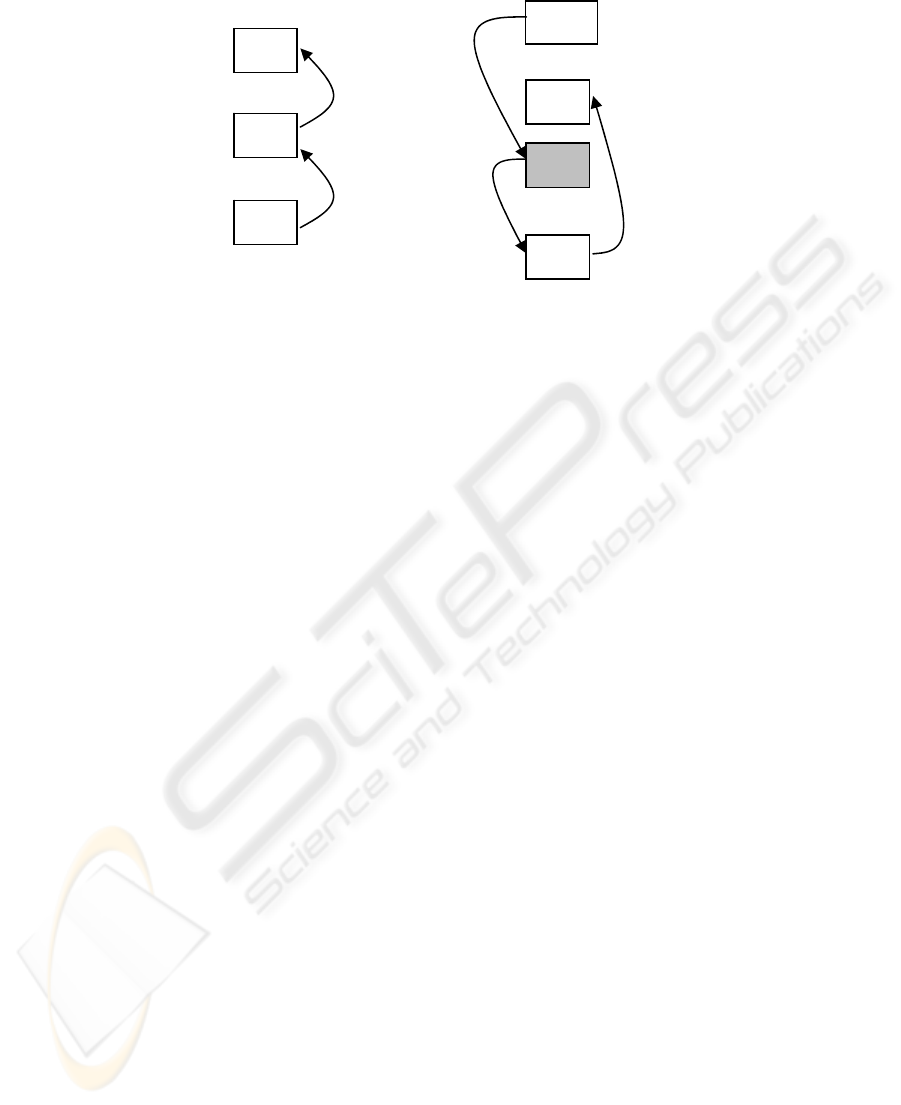
Fig. 1. Minimal Solution Principal

If results of the first step allow improvement, all agents retained in the first step with

their more approximated methods try to propose a more precise method which can be

inter changed with the latest chosen method so that there is no task deadline violation.

We propose an incremental improvement. Each cycle retrieves among all propositions

in terms of duration and quality outcome. The strategy of each agent is to increase its

chance to have its proposition retained. Hence its choice will be focused, among pos-

sible interchanges, on the one, which increase quality outcome with a short duration.

When an agent is retained for its proposition, it is informed, the cost of the coalition is

updated. This will be iterated until the time of the negotiation expires or the cost of

the coalition meets task deadline.

6 Termination and Complexity

6.1 Termination

The termination of the first step is guaranteed, because of the limited number of

agents corresponding to the limited number of levels in one hand, and an agent, which

opts out for the treatment of the task Wj cannot join the coalition again in other hand.

In second step, when the improvement is adopted, the minimal solution is improved

incrementally. One method is interchanged by cycle. The maximum number of cycles

Ccomp, End-Time,

Umin,

arg(Umin),Task-ref

(a) Before task deadline violation: Update of the coalition cost, the

expected End Time and the value of the minimal utility and its owner

(b) Expectation of task deadline violation at a level of

with

arg(Umin)=

c receive an invitation to opt out message

d send to low level neighbour

the identity of

its new up level neighbour

e the coalition formation is resumed from the agent

(

)

(b)

Ccomp,End-Time

,Umin,

arg(Umin),Task-ref

in worst case is

∏

∈Gammai

, where iM

is the cardinality of the set iM

. The termination

of the second step is also guaranteed because of limited number of methods at the level of each

agent.

6.2 Complexity

In the first step we can have backtracking when a violation of the task deadline is ex-

pected. The worst case backtracking is the one where the evaluation of coalition cost

has progressed until the last agent then the violation of task deadline is detected and

the agent with the minimal utility is situated at the bottom of the hierarchy. Example:

for n=5, the evaluation of coalition cost is done from agent 1 to agent 5, at the last

level the violation is expected, the agent with the minimal utility is situated at the bot-

tom of the hierarchy which corresponds to agent of level 2 (agent of the first level is

the mandatory agent). The complexity of a worst case backtracking for

n agents is

O(n). For (n-1) possible backtrackings the complexity of the first step in worst case is

O(n

) .

The second step leads to

∏

∈Gammai

cycles in worst case. The number of exchanged

messages in each cycle is

O(n), in the whole step II the number of exchanged mes-

sages is

∏

∈Gammai

* n).

7 Conclusion

We present an agent approach for the maximization of task utility response. Agents

are cooperative. Each agent is given a set of alternative methods from the more ap-

proximate one to the more precise. The treatment of tasks is done progressively from

agent of level 1 to agent of level

k. The architecture of our system is then structured in

levels. To respect task deadline, one or more levels, represented by agents, can be

skipped except the first level represented by the mandatory agent

The target system is flexible and can adapt itself to the load of each agent for respond-

ing to tasks in delays. Responses will be of quality less or better depending on the

methods that has been used.

Works on agent coordination under time constraints in dynamic environment using

progressive reasoning paradigm were already been proposed like PGPP [6] [7], PGFS

[5].

In these approaches agents are self-interested and share a common environment. Each

agent decomposes its goal in PLPs and controls them. In our proposition agents have

a limited rationality. Our approach is an “agentification” of reasoning level where

each agent is equipped with multiple methods. Agents interactions lie on communi-

cating their temporal information so that they can plan downstream.

Our approach tries to maximize utility of responses to tasks; the quality of the re-

sponse depends on the quality of treatments given to tasks performed by agents.

These treatments consist in progressive improvement of the quality of task solution.

The progressive treatment of each task is distributed among agents; this remains cen-

tral in each agent in PGPP and PGFS.

In this paper we did not address the execution of the task and hence we don’t address

how agent react when the

End Time of an executed method is earlier than expected.

Recall that agents plan using the worst-case performance of their methods, this leads

to not use resource efficiently even if the expected cost of the coalition will always

respect the task deadline in worst-case. Furthermore our cooperative task scheduling

relays on uncertain information. To deal with unexpected situation we need additions

to the scheduling algorithm and monitoring of method performance. Particularly,

when an agent opt out for the treatment of a given task, because of its minimal utility,

which relay on uncertain information. When it detects that it has over estimated its

response time, we want to give it the possibility to repair by asking to join the coali-

tion with its new temporal constraints.

Another solution to explore is to distribute each method among agents. We have one

method by agent. At this moment, the problem is resumed to make two types of coali-

tions, the first one is selective which choose one agent among a set of agents which

have similar methods but different in their performances. The other type is associa-

tive, it concerns agents already selected in the first step.

References

1. Alain Garvey and Victor Lesser. Design-to-time real-time scheduling. IEEE transaction on

systems, man, and Cybernetics, 23(6): 1491-1502, 1993.

2. Abdell-Illah Mouaddib. Contribution au raisonnement progressuf et temps reel dans un

univers multi-agents. PhD thesis, University of Nancy I, (in French), 1993

3. Abedel-Illah Mouaddib and Shlomo Zilberstein. Handling duration uncertainly in meta-

level control of progressive reasoning. Fifteenth International Joint Conference on Artifi-

cial Intelligence, 1201-1206, 1997

4. David J.Musliner, James A.Hendler, Ashok K.Agrawala, Edmund H.Durfee, Jay

K.Strosnider and C.J.Paul. The Challenge of real-Time AI. Computer 28(1): 58-66, January

1995

5. Abdel-Illah Mouaddib. Multistage negotiation for distributed scheduling of resource-

bounded agents. In AAAI Spring Symposium On Satisfiying Models, pp 54-59, 1998.

6. Abdel-Illah Mouaddib. Anytime coordination for progressive planning agents. in AAAI-

99, pp 564-569, 1999.

7. Abdel-Illah Mouaddib. Incremental Coordination for Time-Bounded Agents.Iin Interna-

tional Journal On Artificial Intelligence Tools 13(3):511-531, September 2004.

8. Shlomo Zilberstein and Abdel-Illah Mouaddib. Reactive control for dynamic progressive

processing. In IJCAI, pp 1269-1273, 1999.