USING RELEVANT SETS FOR OPTIMIZING XML INDEXES

Paz Biber, Ehud Gudes

Dep. of comp. science, The Open U., Rabotzki 108, Ra'annana, Israel

Keywords: Local bisimulation, Relevant set, A(k)-Index, Partial order relation.

Abstract: Local bisimilarity has been proposed as an approximate structural summary for XML and other semi-

structured databases. Approximate structural summary, such as A(k)-Index and D(k)-Index, reduce the

index's size (and therefore reduce query evaluation time) by compromising on the long path queries. We

introduce the A(k)-Simplified and the A(k)-Relevant, approximate structural summaries for graph

documents in general, and for XML in particular. Like A(k)-Index and D(k)-Index, our indexes are based on

local bisimilarity, however, unlike the previous indexes, they support the removal of non-relevant nodes.

We also describe a way to eliminate false drops that might occur due to nodes removal. Our experiments

shows that A(k)-Simplified and A(k)-Relevant are much smaller then A(k)-Index, and give accurate results

with better performance, for short relevant path queries.

1 INTRODUCTION

XML (eXtensible Markup Language) has rapidly

become the data representation language of choice

for information exchange on the web (Bray, T., et

al.), (Busse, R., et al, 2001). XML document is a

semi-structured database (Buneman, P., et al, 1997),

(Li, Q. and Moon, B., 2001) , i.e. can be described as

a directed graph. In Figure 1 we see an example of a

graph representing a semi structured database. As

with relational databases, evaluating queries using

only the original database can be very costly in

terms of time and resources needed. Clearly, an

index is needed for an efficient evaluation. Several

types of indexes were suggested, such as connection

indexes, which are designed to support ancestor-

descendent connection, like HOPI (Schenkel, R. et

al., 2004), but most of the indexes proposed are

based on structure summary of the document.

Existing structure summaries are based on NFA to

DFA transition like Strong DataGuide (Goldman, R.

and Widom, J., 1997), graph index with hash tree to

support common prefixes, like APEX (Chung, C. W.

et al., 2002), and bisimilarity based summaries like

1-Index (Milo, T. and Suciu, D., 1999), (Kaushik, R.

et al., 2003) , T-Index (Milo, T. and Suciu, D.,

1999), F&B-Index (Kaushik, R. et al., 2002), A(k)-

Index (Kaushik, R. et al.) and D(k)-Index (Qun, C.,

Lim A. and Ong, K. W., 2003).

In this paper we introduce A(k)-Simplified and

A(k)-Relevant – a structure summary of a semi

structured database, based on local bisimilarity,

which supports removing nodes with non relevant

tags (and therefore significantly decreasing the index

size), while saving the document structure, so short

queries can still be answered accurately. The main

assumption our indexes is based upon is that we can

classify the tags into 2 groups: relevant and non

relevant (as mentioned in (Kaushik, R. et al.,

2002),(Qun, C., Lim A. and Ong, K. W., 2003)). By

declaring a tag as a relevant tag we either mean that

the expression paths are built from relevant tags only

– and we have A(k)-Simplified to support query

evaluation, or, we mean that the results

will be

composed of relevant tags only – and we have A(k)-

Relevant to support these queries. The proposed

approximate indexes are much smaller then A(k)-

Index, and therefore give much better processing

time results. Additional contributions in this paper

are:

1. Presenting a method to eliminate false drops in

A(k)-Simplified and A(k)-Relevant (with respect to

A(k)-Index) using partial order. This method

increases the size of the indexes only by a tiny

amount, and uses data saved on a small percent of

the edges.

2. Showing experimentally that A(k)-Simplified and

A(k)-Relevant reduce both the size of the index and

the processing cost (compared to A(k)-Index). We

also examine the indexes behavior when evaluating

queries with length greater then k.

The idea of replacing irrelevant tags with the label

"other", as a method to reduce index size, appeared

Biber P. and Gudes E. (2005).

USING RELEVANT SETS FOR OPTIMIZING XML INDEXES.

In Proceedings of the First International Conference on Web Information Systems and Technologies, pages 13-23

DOI: 10.5220/0001229400130023

 SciTePress

already both in (Milo, T. and Suciu, D., 1998) and

(Kaushik, R. et al., 2002). However, both papers do

not elaborate on the algorithmic implications of this

idea, and in the context of A(k)-Index. This

algorithmic elaboration is the main contribution of

this paper (see also section 2).

The rest of the paper is organized as follows: We

review existing work in section 2, then we elaborate

on the data model and other related issues in section

3 – preliminaries. Afterwards we describe A(k)-

Simplified and A(k)-Relevant in section 4, and then

we give a way to remove false drops in section 5.

We then conclude with experimental results (section

6) and further research (section 7).

2 RELATED WORK

In semi-structured databases, indexes are structural

summaries, made to reduce time for query

evaluation. Some of the indexes are approximate,

which means that for some queries, verification is

needed in order to remove false drops (by the term

false drops we mean false positive – some of the

index's results are incorrect). Examples for such

indexes are: Approximate DataGuide (Goldman, R.

and Widom, J., 1999), which is based on Strong

DataGuide in which “similar” nodes are merged,

APEX (Chung, C. W. et al., 2002) – An index that

adjusts its structure using data mining strategies in

order to efficiently evaluate queries with common

suffixes, D(k)-Index (Qun, C., Lim A. and Ong, K.

W., 2003), which uses different local bisimilarity

values in order to emphasize important tags, and

A(k)-Index. In our work we are interested in the

A(k)-Index and local bisimilarity on which it is

based. We say that two nodes are bisimilar if the two

groups of incoming label path are similar. Every

node in a bisimilarity based index is an equivalence

class for the bisimilar relation. The first bisimilarity

based index was 1-Index, which is safe and accurate

but tends to be very large, especially with “complex”

documents. A(k)-Index offers a way to reduce the

index size by relaxing the bisimilarity demand for

having all the incoming label paths, and declaring a

new relation – local bisimilarity. Two nodes are k

local bisimilar, if their two groups of incoming label

paths, not longer than k, are similar. Local

bisimilarity is based on the assumption that long

queries are rare, and therefore we can build a

structure that gives accurate results for short queries,

while in long queries the results are approximate,

and sometimes need verification (i.e. A(k)-Index is

safe). Experiments show that A(k)-Index is much

smaller then 1-Index.

In A(k)-Index both relevant and non-relevant tags

gets the same treatment, because we define one k for

all the index, in D(k)-Index we can emphasize

relevant tags by giving the nodes with the desired

tags different ‘k’ (local similarity) value, however,

in spite the fact that some tags are known to be non

relevant at all, D(k)-Index still includes all the nodes

whether their tags are relevant or not.

As seen in (Kaushik, R. et al., 2002),(Milo, T.

and Suciu, D., 1998) using partial data can improve

evaluation time. The schema in (Milo, T. and Suciu,

D., 1998) is based on simulation and is used for

creating efficient regular path expressions, which

improves DB scanning time. "other" edges are used

as a replacement for unknown tag's edges which

exist in the DB. However, the goal of the data

structure in (Milo, T. and Suciu, D., 1998) differs

from the goal of (Kaushik, R. et al., 2002) and ours.

We use a bisimulation data structure to efficiently

evaluate the query, rather then creating a more

efficient one, both (Kaushik, R. et al., 2002) and us

offer a method to reduce the index size, by replacing

irrelevant tags with the tag "other", and removing

isolated "other" nodes. This method allows an

efficient evaluation of queries based on relevant tags

only. (Kaushik, R. et al., 2002) uses this method to

reduce the F&B index size, but does not give

detailed algorithms for constructing the index and

evaluating the query using "other". We present these

algorithms in depth, especially in the context of

A(k)-Index structure, and exploit the local

bisimulation in treating "other" nodes. A(k)-

Simplified uses this idea and adds a method to

remove "other" node's path, and A(k)-Relevant

exploits local bisimilarity and relaxes the demand

for queries with relevant tags only, by just requiring

a relevant tag at the end of the query and therefore

supports all queries which return relevant data. Both

indexes support the collapse of "other" paths without

introducing false results.

3 PRELIMINARIES

XML or other semi-structured databases are

modeled as a directed, labeled graph G, with each

edge indicating an object-subobject or object-value

relationship. Each node in G has a label, and an OID

(as described in (Papakonstantinou, Y., 1995)), with

simple objects having a distinguished label,

VALUE. In Figure 1 we can see an example of a

semi structured data graph. The id-idref edges are

sketched with dotted line, but in our model, we

consider all the edges in the same manner. Queries

in semi structured databases are based on regular

path expression. Let G be a data graph, and Σ

WEBIST 2005 - INTERNET COMPUTING

the set of labels in G, we define a regular path

expression R as follows: R := L | _ | R.R | (R|R ) |

R*, where L∈ Σ

, ‘_’ denotes any label (one label

only), ‘.’ denotes sequence, ‘|’ alternation and ‘*’

denotes repetition. From now on, we will use a

common abbreviation – the sign “*.” will replace

“_*.”. Before explaining the usage of regular path

expressions, we give some formal definitions. A

node path in G is a sequence of nodes, n

, n

,… n

such that n

∈G, and an edge exists between n

and

i+1

for 1≤i≤m-1 . A label path is a sequence of

labels l

, l

,… l

. A node path matches a label path if

label(n

)=l

for 1≤i≤m. We denote L(R) to be the

regular language specified by R, and we say that R

matches a data graph node n if there is a label path

for some word in L(R) that matches a node path

ending in n. Now, the result of evaluating a query R

on a data graph G, is the set of nodes in G that

matches R. for example, the path expression

*.movie.title evaluated on Figure 1 data graph, is all

the movie’s titles.

Each node in the index graph is associated with

an extent, which is the set of nodes in the matching

equivalence class. If an edge exists from a node in

one equivalence class to a node in another

equivalence class, we add the appropriate edge to the

index. We denote the index for data graph G as I

Evaluating a query, which is a regular path

expression R on I

is a union of the extents of index

nodes in I

that matches R.

Definition 1. (Safe and Accurate) Let R be a

regular path expression, we say that an index I

safe if for each node

v∈V

, if R matches v, then v is

in the result of evaluating R on I

. We say that I

accurate if for each node

v∈V

, R matches v if and

only if

v is in the result of evaluating R on I

Definition 2. (Reversed Bisimulation) Let G be a

data graph in which the symmetric, binary relation

≈, the reversed bisimulation, is defined as : two

nodes

u and v are bisimilar (u ≈ v), if:

1. u and v have the same label.

2. if u’ is a parent of u, then there is a parent v’ of v,

s.t. u’ ≈ v’, and vice verse.

Definition 3. (Local Bisimulation – k-

Bisimilarity) Let G be a data graph in which the

symmetric, binary relation ≈

, the local bisimulation,

is defined inductively: given the local similarity

value k, we define two nodes u and v to be k-

bisimilar (u ≈

v) recursively:

1. u ≈

v iff u and v have the same label.

2. u ≈

v iff u ≈

k-1

v and for every parent u’ of u, there

is a parent v’ of v, s.t. u’ ≈

k-1

v’, and vice verse.

If two nodes are bisimilar then all the incoming

label paths are equal, while if two nodes are k-

bisimilar, then all the incoming label paths not

longer then k, are equal. 1-Index and A(k)-Index are

based on bisimulation and k-bisimilarity

respectively. We note that 1-Index is accurate while

A(k)-Index is safe. In Figure 1 we see an example of

A(0)-Index (label split index), A(1)-Index and 1-

Index for the data graph shown in Figure 1. Each

index node has its extent attached.

A command is the basic instruction that a script

file contains. Some commands require parameters

that further define what the command should do. An

expression is a combination of operators and

arguments that create a result. Expressions can be

used as values in any command. Examples of

expressions include arithmetic, relational

comparisons, and string concatenations.

3.1 The Set L

Normally we can split our DB into relevant and

irrelevant data (with respect to the queries on the

database). For example, in our movie database we

might want to query only movies or actors so

director and director’s name are irrelevant. We split

the database by defining L (L ⊂ Σ

) to be the set of

relevant tags in the database. We will see later in

this paper that by exploiting the existence of L, we

can reduce the index size and query evaluation time

significantly. By defining L, we should consider two

types of queries containing relevant tags:

1. Relevant queries. Queries built only on relevant

tags. i.e. the query is a regular path expression R,

Figure 1: Semi structured database represented as a graph, 1-Index and A(k)-Index

(b) A(0)-Index (c) A(1)-Index (d) 1-Index (a) Database

MovieDB

3,5

N M

6,10

7,11

9,13

MovieDB

3,5

N M

6,10

7,11

9,13

MovieDB

2,4

8,12

6,10

3, 5, 7,11

9,13

MovieDB

2,4

8,12

6,10

3, 5, 7,11

9,13

MovieDB

“actor1”

“actor2”

“director1”

“movie2”

“director2”

“movie1”

MovieDB

“actor1”

“actor2”

“director1”

“movie2”

“director2”

“movie1”

USING RELEVANT SETS FOR OPTIMIZING XML INDEXES

R=r

. … r

, and for i=1,…,n-1, r

∈L ∪ {‘*’,

)}, r

∈L

2. Relevant end queries. Queries that end with a

relevant tag. This means we have relevant tags as

our results, but irrelevant tags can be a part of the

queries. We define those queries as a regular path

expression R, R=r

. … r

, and for i=1,…,n-1,

∈V

∪ {‘*’, (r

)}, r

∈L.

The symbol “_” was not mentioned, but since we

are using a relevant set, it can be used in queries

only in order to replace a relevant tag.

In this paper we will propose 2 indexes: A(k)-

Simplified and A(k)-Relevant. These indexes exploit

the existent of L in order to reduce index size and

query evaluation time. A(k)-Simplified is very

efficient when evaluating queries from the first type

(relevant tags only), while A(k)-Relevant supports

both type of queries, and is preferred when dealing

with queries which contains irrelevant tags along the

path. A(k)-Simplified and A(k)-Relevant are very

efficient when L is defined, and the queries comply

with one of the two types. If this is not the case,

using these indexes may result in false drops. The

term 'relevant' will be used both when discussing

tags and nodes with relevant tags. The meaning will

be clear from the context.

4 A(K)-SIMPLIFIED AND A(K)-

RELEVANT

4.1 Introduction to A(k)-Simplified

and A(k)-Relevant

A(k)-Simplified index is based on k-bisimilarity by

the fact that we preserve all the incoming paths with

length less or equal to k. furthermore, giving the set

L, each tag in A(k)-Simplified is either from L or

“other”. A(k)-Simplified is built by replacing all the

irrelevant tags by the tag “other”, and then replacing

an “other” tree with one “other” node. A(k)-

Relevant is also based on k-bisimilarity, but in this

index, besides the relevant tags and the tag “other”,

we preserve the tags of nodes that have a relevant

descendant in distance not greater than k (we will

elaborate later in this section). A(k)-Simplified is the

index which results from the following 4 steps (see

also section 4.2): Replacing all the irrelevant tags

with the tag “other”, Removing all the nodes with

tag “other” with no relevant descendent node,

Applying the A(k)-Index building algorithm,

Replacing every “other” node tree with one “other”

node. Before building A(k)-Relevant there are 2

important issues that should be considered:

1. Like A(k)-Simplified, if there is an “other” node

from which we cannot reach a relevant tag node,

then the “other” node can be removed.

2. A(k)-Index properties suggest that two data graph

nodes

u, v will be in the same extent if all the

incoming label paths with length ≤ k are the same,

and there is a node with tag T which is k+1 steps

from

u and which is not matched by any node

with tag T and k+1 steps from

v. Since A(k)-

Relevant supports queries that end with relevant

tag nodes, we can conclude that there is no need

to preserve the tag of irrelevant nodes with

distance k+1 or more from a relevant node.

Building A(k)-Relevant is quite similar to

building A(k)-Simplified, with a small modification

in the first step: Replacing all the irrelevant tags of

nodes with no relevant tag descendent within

distance less or equal to k with the tag “other”.

A(k)-Simplified and A(k)-Relevant have the

following properties (w.r.t A(k)-Index (Kaushik, R.

et al.), (Qun, C., Lim A. and Ong, K. W., 2003)) :

1. For relevant tags, which are our main (and usually

all) interest, A(k)-Relevant keeps all paths with

length ≤ k (and therefore accurate for those

queries). Using false drops removal, A(k)-

Simplified is also accurate for relevant queries

with length ≤ k.

2. A(k)-Simplified and A(k)-Relevant are safe.

For k values large enough, A(k)-Simplified and

A(k)-Relevant do not change (they have a steady

structure) and they can be considered as 1-Index

with relevant support.

4.2 Construction Algorithms

We first describe the A(k)-Simplified construction

algorithm and then the modifications needed for

building A(k)-Relevant. The construction algorithm

has 4 steps:

1. Collapse – replacing irrelevant tags with the tag

“other”, and removing irrelevant nodes which

have no relevant descendent.

2. A(k)-Index – creating an index structure where k-

bisimilar nodes are combined to the same extent.

3. MaxOtherPath – marking the “other” trees.

4. Replacing other trees – replacing the trees

marked in step 3 by one “other” node.

Algorithm 1: Collapse

Input: The inversed data graph G’=(V,E).

Output: The data graph G with irrelevant tags

replaced with the tag “other”, and irrelevant nodes

with no relevant descendent removed.

1. Empty (Q)

2. for each vertex v∈V(G) do

WEBIST 2005 - INTERNET COMPUTING

3. If v∈L (Relevant) then Distance(v) = 0;

Status(v) = "Visited"; Enqueue(Q,v)

4. Else Distance(v) = ∞; Status(v) = "Not

Visited"; Label(v) = "other"

5. While Q is not Empty

6. u = head(Q)

7. for each s son of u do

8. if Status(s) = "Not Visited" then

Status(s) = "Visited"; Distance(s) = Distance(u)

+ 1; Enqueue(Q,s)

9. Dequeue(Q)

10. Status(u) = "Finished"

11.Remove all vertices with Distance = ∞ and

Reverse G’ back to G

We can see the collapse running example in

Figure 2. We remark that the input is G’ (G

reversed) because the distance is calculated from the

descendents to their parents. We will also remark

that in step 8 we save the distance from a irrelevant

node to a relevant node. This is not important here

(in A(k)-Simplified we are only interested to know

whether it is ∞ distance (no path) or not). We will

use this parameter later, when we describe A(k)-

Relevant. The algorithm is based on BFS with some

modifications – we traverse G’ – the reversed graph

and initialize the next node queue with all the

relevant nodes (the grey nodes in Figure 2 will

become clearer when we describe A(k)-Relevant)

As stated earlier, the next step is applying A(k)-

Index to Collapse’s result. The algorithm is

described in (Kaushik, R. et al.). The third step is

MaxOtherPath - this algorithm is based on depth

first search, where for each “other” node we

encounter – we either relate it to the current path (if

exist) or start a new path. The motivation is to mark

"other" nodes trees before replacing each one with a

single node.

Algorithm 2: MaxOtherPath

Input: The result of the second step (A(k)-Index) –

the index graph G.

Output: The index graph G with each “other” node

related to an "other" tree. Each "other" tree has a set

of all incoming and outgoing edges.

1. Global-Current-Tree = 0

2. For each vertex u∈V(G) Visited(u) = Never;

Path(u) = Global-Current- Tree

3. MaxOtherPath-DFS-Visit(root, False, 0)

MaxOtherPath-DFS-Visit

(u, Path-Indication,

Current-Tree)

1. Visited(u) = Visited

2. if u∈L (i.e. Relevant) then Tree -Indication =

False

3. Else

4. If Tree -Indication = False then Path-

Indication = True; Global-Current-Tree =

Global-Current-Tree +1; Current-Tree =

Path(u) = Global-Current-Tree

5. Else Path(u) = Current-Tree

6. For each v∈Son(u)

7. If Visited(v) = Never then

8. MaxOtherPath-DFS-Visit(v, Path-Indication,

Current-Tree)

9. For each path found – walk through the nodes

and for every edge not part of the path add it to

incoming set or outgoing set according to the

edge origin.

We can see an example of MaxOtherPath in

Figure 3. The last step of the construction algorithm,

is replacing each “other” nodes tree by one “other”

node. This is done simply by removing all the

“other” nodes and their edges and replacing them

with one node with tag “other”. For every incoming

and outgoing edge we saved in step 9 in

MaxOtherPath, we add the appropriate edge to our

new node (see

Figure 3d). Note that if instead of

replacing every “other” tree, we replace all the

“other” nodes with one node, we may add many

false drops, and this may cause a lot of verifications

when we process the queries, and therefore

substantially increase time for evaluating the

queries. We will also note that self edges will be

created when we have 2 (or more) “other” paths

(paths built on “other” nodes only) from one “other”

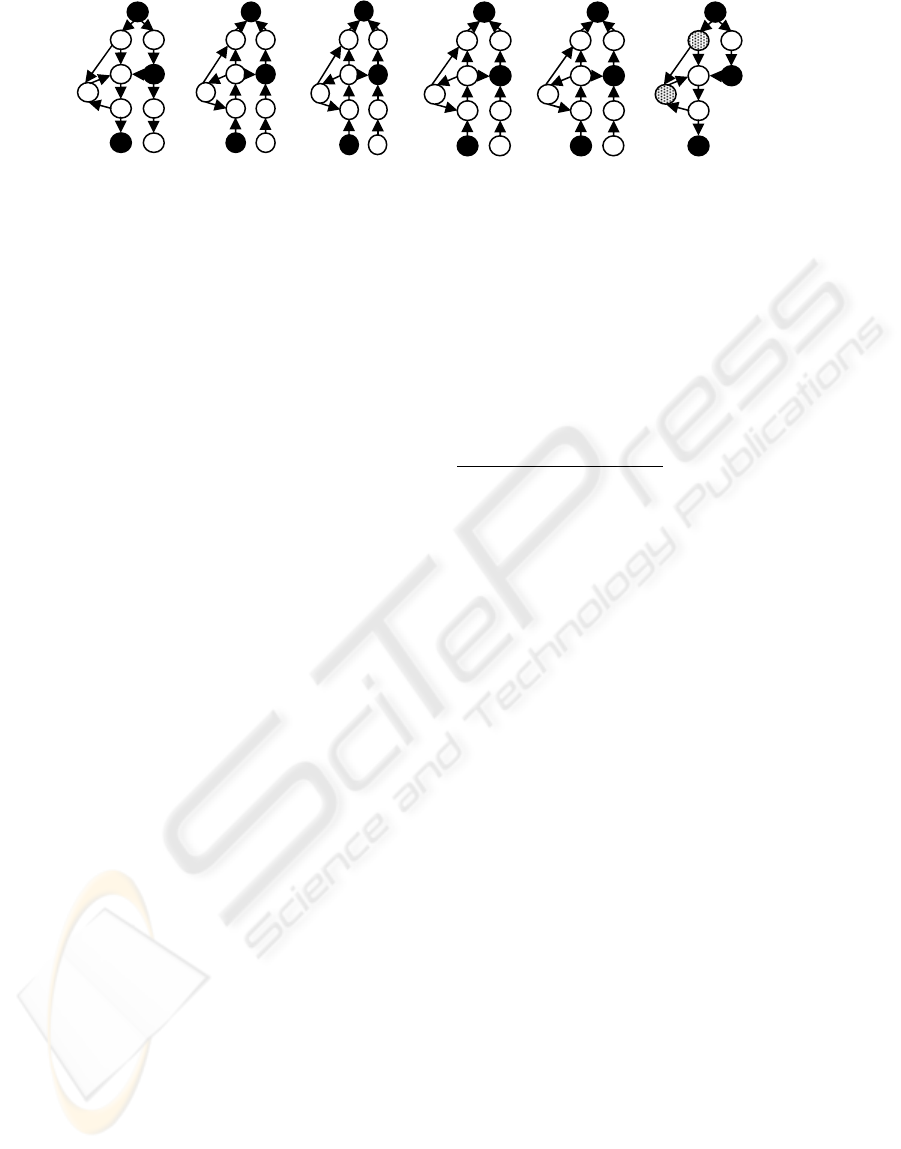
Figure 2: collapse algorithm (k=2): (a) the original data graph (relevant notes are black, irrelevant nodes –

white) (b) the reversed graph, (c)-(e) three passes of steps 12-18, (f) result

(a)

original

(b) the

inversed

pass

(d) after

second pass

(e) after

third pass

(f) collapse

result

∞

USING RELEVANT SETS FOR OPTIMIZING XML INDEXES

node to another. For now, self edges can be omitted;

we will discuss this in the next section – removing

false drops.

Until now we discussed A(k)-Simplified

building algorithm. As we have already seen, the

difference between A(k)-Simplified and A(k)-

Relevant is that the former replaces the tag of all the

irrelevant nodes with the tag “other”, while the latter

only replaces the tag of irrelevant nodes with distant

relevant descendent (distance > k). In order to

achieve this, we have to modify the first step

(collapse). The modifications are: k will be added to

the input for the algorithm, and instead of replacing

all the irrelevant nodes, we will replace only those

nodes which have distance > k. In Figure 2f, we

marked with gray dots the irrelevant nodes which

will not be tagged as “other”. If the data graph is

G=(V,E), the total constructing time is O(k

⋅

|E|)

(A(k)-Index time complexity). In more details, we

have the time complexity O(|E|) for collapse (BFS

complexity), O(k

⋅

|E|) (Kaushik, R. et al.) for A(k)-

Index, O(|E|) for MaxOtherPath (DFS complexity)

and O(|E|) for replacing other trees (removing

irrelevant nodes, and restoring all the effected

edges).

Theorem 1. A(k)-Simplified is safe for l

≤

relevant queries. A(k)-Relevant is safe and accurate

for l

≤

k relevant end queries.

Proof. Obvious from the indexes definitions.

5 REMOVING FALSE DROPS

As mentioned earlier, replacing the “other” trees

may result in increasing number of false drops (w.r.t.

A(k)-Index). In

Figure 4 we can see that replacing

the irrelevant tree increases the number of false

drops in A(k)-Simplified for paths with length < k

(in

Figure 4b the dotted line shows the path which

does not exist in the original data graph). A(k)-

Relevant is accurate for short relevant end queries,

however, in

Figure 4 we see an example where for

path longer than k, A(k)-Relevant adds false drops

which are not returned by a lookup in the A(k)-

Index. In

Figure 4c the dotted line marks the result

of the query R.A.*.B. In

Figure 4d we see the result

of this query on A(4)-Relevant, which includes one

false drop.

The reason for increasing number of false drops

w.r.t. A(k)-Index is that we replace the “other” trees

with one node and add paths which do not exist in

the original graph. From these observations we see

that removing invalid paths involving “other” nodes

can reduce the number of false drops for A(k)-

Simplified (for queries in any length) and for A(k)-

Relevant (query’s length > k). In this section we will

present a method to remove these invalid paths. For

each “other” tree replaced by one node, we mark the

location of every incoming and outgoing edge, and

use these marks in query calculation. We now

describe a way to mark the edges using a partial

order relation.

5.1 Partial Order Relation

The intuition for using partial order relation is the

observation that it stands for the relation

"descendent of" between 2 nodes in an "other" tree

discovered by collapse, and therefore, by keeping

the partial order relation between the nodes we can

reconstruct the original paths, and remove the false

paths.

We save the location of every node in each

“other” tree

in the following way: p

;…;p

(n>0). p

represents the path from the root to the

node, d represents the node’s depth. By the term

“other” tree we mean the sequence of “other” nodes

discovered during the MaxOtherPath algorithm. The

meaning of p

is: We mark the first “other” node

discovered in the “other” path (the path’s root) by ;1

which stands for depth 1 (d=1, i=0). Assuming we

are in an “other” node

u which is marked with

;…;p

;d then:

1. if

u does not have an “other” child node there

is nothing to do.

2. If

u has exactly one “other” child node, it will

be marked with p

;…;p

;d+1

3. if u has k>1 “other” children nodes, their mark

will be: p

;…;p

;d;1;d+1, ...,

Figure 3: MaxOtherPath and “other” tree replacement algorithm

(a) original

data graph

(b) partial results

of MaxOtherPath

result

(d) Replacing “other”

tree with one node

WEBIST 2005 - INTERNET COMPUTING

;…;p

;d;k;d+1. (we concatenate m;d+1 for

u’s m rightmost “other” child).

We can now define our partial order relation.

Assume that A=a

;…;a

, B=b

;…;b

(A,B represent two locations in an “other” path), we

define the relation “≤’”: A≤’B if a

;…;a

⊂

;…;b

;…;a

is not equal but is a prefix

of b

;…;b

) or if a

;…;a

;…;b

and

≤d

. This is a partial order relation – it is reflexive,

antisymetric and transitive. We will see later on, that

given 2 nodes u,v in an “other” tree there are three

possibilities, either there is a path from u to v (which

translates to Mark(u)≤’Mark(v)), a path from v to u

(Mark(v)≤’Mark(u)) or there is no path at all (no

relation between the Mark(u) and Mark(v)). After

defining the relation ≤’, we should mark the “other”

nodes and take this mark into consideration when

querying the index. In MaxOtherPath, when we

traverse an “other” tree we keep two parameters:

trail and depth, and we mark each node with

trail;depth, the trail corresponds to p

,..,p

and the

depth corresponds to d. when replacing the "other"

nodes tree with one “other” node we give each

ingoing/outgoing edge two values: ingoing mark and

outgoing mark. If the origin of the edge is from a

relevant node (not an “other” node) its origin mark

will be null, else, its origin mark will be the “other”

node’s mark. We treat the node’s destination mark

with a same manner. In

Figure 5 we can see an

example of how we mark each node in the “other”

tree, and how we use those marks to mark the origin

and destination of the appropriate edges.

5.2 Handling Self Edges

Both in A(k)-Simplified and A(k)-Relevant

construction algorithms, self edges could have

been formed when there where 2 (or more) “other”

paths (paths built on “other” nodes only) from one

“other” node to another. Those self edges were

removed because they did not contribute to query

analysis. However, when we add the false drops

treatment, self edges play an important role. More

information regarding self edges and self edges

removal is given in (Biber, P. and Gudes, E., 2005).

Theorem 2. False drops removal eliminates the

invalid paths formed when “other” tree is replaced

by one “other” node.

Proof. In order to show that no invalid path is

added, we will see that there is a path from a node u

to a node v (u and v are both a part of the same

“other” tree, as found by MaxOtherPath) if and only

if Mark(u)≤’Mark(v). if u is an ancestor of v, then

v’s trail is either equal to u’s or has u’s mark as its

prefix – either way Mark(u)≤’Mark(v). The

implication holds also in the opposite direction,

since if Mark(u) ≤’ Mark(v) it means that either v’s

trail is equal to u’s and v’s depth is greater then u’s

or v’s trail has u’s mark as its prefix.

€

From the A(k)-Index and the false drops removal

properties we get the following:

Corollary. When using false drops removal,

A(k)-Simplified is accurate for short relevant

queries, and A(k)-Relevant has less false drops for

l>k relevant end queries.

5.3 Querying the Indexes

Without false drops treatment, the way to compute a

query is equal to the one described in (Kaushik, R.

et al.). In

Figure 6a we can see an example of an

index (it can be Relevant or Simplified), a DFA that

matches the query *.A.B (

Figure 6b), and the results

of the index scan (

Figure 6c) without taking the

marks into consideration. The returned set is the

extent of the index nodes that get an accepting state

(state 3, marked with an arrow). In order to take

advantage of the false drops removal's markings

added to the index, the scanning must consider two

(a)

(b)

(c)

(d)

Figure 4: false drops in A(k)-Simplified and A(k)-Relevant: (a) Original data graph (which is equal to A(3)-

Index). L={A}. (b)

The appropriate A(3)-Simplified. The dotted line represents a path which does not exist in A(3)-

Index (c) Original data graph

(which is equal to A(4)-Index), L={R,A}. The dotted line represents the results of the query R.A.*.B (d) The appropriate A(4)-

Relevant. The dotted line represents the result of the same query on the index (the left B node is a false drop)

USING RELEVANT SETS FOR OPTIMIZING XML INDEXES

factors: the edges marking and the self edges. In

Figure 6d we can see the results of the same query

evaluated with marks. In

Figure 4c when the nodes

C6, C7, C1 were translated to “other” nodes, they

got the marking: ;1, ;1;1;2 and ;1;2;2 respectively,

so in

Figure 4d the edge between A and O has a

destination mark 1;1;2 , the edge from O to C2 has

an origin mark 1;1;2 and the edge from O to C8

an origin mark 1;2;2. Now, since 1;1;2 has no ≤’

relation with 1;2;2 when we process the query

R.A.*.B and enter the “other” node from A, we will

not be able to go to C8 and the false drop will be

removed.

6 EXPERIMENTAL STUDY

In this section we present the results of the

conducted experiments. This section layout is as

follows: first we give some background regarding

queries, the cost model, the selection of the relevant

set L and the databases used in the experiments, next

we examine the indexes size and the increase of size

due to false drops removal, afterwards we compare

the time needed to scan the indexes when processing

queries and in the last section we examine the

number of false drops.

6.1 Experimental Framework

Query classification

In our experiments we use a slightly different

classification than the one presented in (Kaushik, R.

et al.). We split the queries into 3 groups:

• Short queries which are queries built on labels

only – for example L

. It is clear that for

short and - relevant or relevant end query -

A(k)-Simplified with false drops removal and

A(k)-Relevant (respectively) are accurate.

• Simple queries which are queries that have

only one “*” located at the beginning of the

queries – for example *.L

. although when

processing these queries we use paths longer

then k, it can be easily shown that the indexes

are still accurate.

• Complex queries which have more then one

“*” or only one “*” but not as the query’s

starting label. When processing these queries

all of the indexes (including A(k)-Index) may

return false drops, so verification might be

needed.

The experiments results include false drops

verification (whenever it is need). As expected,

verification is needed for complex queries, or when

k is very small.

The cost model

We will use the cost model offered in (Kaushik, R.

et al.). The cost of evaluating a query is the number

of nodes visited in the index during automaton

execution plus the number of nodes visited in the

DB during false drops verification. Note that for

precise queries no verification is needed. The graph

size is calculated as the sum of the graph nodes and

edges.

Selecting the relevant set L

In our experiments, we randomly selected various

sets of relevant labels. There are two ways to

examine the relevant set: the percent of nodes out of

all the data graph nodes which have the relevant tags

or, the percent of the relevant tags out of all the tags

in the database. Our experiments show that the

former is a better measure to predict the indexes size

and accuracy. We also randomly selected the

relevant set, so usually the nodes will be spread all

over the graph, however, in some cases the nodes

will not be spread homogenously so the results can

have some variation, but the experiments always

show a tendency.

The Databases

In the experiments described, two XML databases

were used. The first source is the Internet Movie

Database (IMDB) (The Internet Movie Database

Ltd, “Internet Movie Database”, Available:

http://www.imdb.com) and the second is a synthetic

database generated for performing our experiments.

IMDB was selected because it represents a real life

database with many cycles (Goldman, R. and

Widom, J., 1997). The portion of the database

selected is organized around movie. The synthetic

database is a highly complex database with a lot of

irregularity that allows examining the indexes in

highly irregular conditions, where the index size is

usually very large.

Figure 5: Marking the nodes in the “other” trees, and

the appropriate edges after replacing the trees with

one node

2;2;

2;1;

;

;2;1;3

;2;2;3

;

;2;1;3

WEBIST 2005 - INTERNET COMPUTING

6.2 Index Size

The size of A(k)-Simplified and A(k)-Relevant

increases as k increases but it remains stable

compared to the A(k)-Index’s size. High variation of

the database increases the size of A(k)-Simplified

and A(k)-Relevant (compared to A(k)-Index). The

size of the indexes w.r.t. A(k)-Index is displayed in

Figure 7. The size is calculated for different values

of k, the A(k)-Simplified and A(k)-Relevant are

calculated for different L sets. The size shown in the

graph is the indexes average size over different L

sets, and as we can see A(k)-Simplified is 40%-52%

of A(k)-Index, and A(k)-Relevant is 55%-69% of

A(k)-Index. The increase of size due to false drops

removal (because of self edges addition) is displayed

in the lower figure. As expected, the increase of

A(k)-Relevant’s size is almost zero for small k

values and zero for large k values – since we

preserve the tags of incoming paths with length

smaller or equal to k, the size and complexity of the

“other” paths is reduced and therefore the number of

self edges is also reduced. In A(k)-Simplified the

size increases for larger k, because in the second

step of the building algorithm (A(k)-Index) fewer

“other” nodes merge into one index node, and so in

the fourth step (replacing the “other” trees) more

nodes are replaced and so more self edges are

formed. This trend stops at a certain k value.

6.3 Query Cost

Figure 8 shows the cost of evaluating various

queries. As expected, the queries evaluation cost for

A(k)-Simplified and A(k)-Relevant with or without

false drops removal is much smaller then evaluating

the query on A(k)-Index. Also as k reaches a certain

value, the evaluation cost stops growing, since the

indexes reach their stable state. As mentioned

earlier, the result here are the index scanning cost

plus verification cost (when needed). For complex

queries, there is always a need to verify the query

results (for all the queries). Since complex queries,

like simple queries, contain “*” (one or more) the

proportion between the A(k)-Index scanning time to

the A(k)-Simplified and A(k)-Relevant scanning

time remains quite similar to those of the simple

queries evaluation. The important factor here is the

number of false drops which causes costly

verification. Figure 9 displays the percent of false

drops for complex queries. It is clear that A(k)-

Simplified without false drops removal has more

false drops (and therefore has a costly evaluation

time). With false drops removal the number of false

drops in A(k)-Simplified is reduced by an order of

tens of percents. As expected, for A(k)-Relevant the

increase of false drops number (w.r.t. A(k)-Index) is

very small – less then 0.3% in average (actually it is

0% most of the time) – here the false drops removal

is less effective though we can still see a small

improvement in the synthetic database. We can also

see that for relevant end queries, A(k)-Relevant has

much less false drops than A(k)-Simplified, which

explains A(k)-Relevant's better results.

Figure 6: Evaluating query on an index.

Figure 7: The indexes size. In the upper figure -

comparison between the indexes and A(k)-

Index. In the

lower figure -

the size increase due to false drops

removal (self edges increase).

10%

20%

30%

40%

50%

60%

70%

80%

012345678910

Percent of A(k)-Index

A(k)-Simplified in IMDB A(k)-Relevant in IMDB

A(k)-Simplified in synthetic database A(k)-Relevant in synthetic database

99.00%

99.50%

100.00%

100.50%

101.00%

101.50%

102.00%

012345678910

Percent of indexes without

false drops removal

A(k)-Simplified in IMDB A(k)-Relevant in IMDB

A(k)-Simplified in synthetic database A(k)-Relevant in synthetic database

USING RELEVANT SETS FOR OPTIMIZING XML INDEXES

7 CONCLUSION AND FUTURE

RESEARCH

A(k)-Simplified and A(k)-Relevant are small,

efficient indexes evolved from A(k)-Index. The

indexes offer a way to reduce index size

significantly when prior knowledge of the relevant

tags exists. Though based on A(k)-Index, A(k)-

Simplified and A(k)-Relevant are flexible, and can

be modified to be based on other structured indexes,

such as 1-Index and D(k)-Index. A(k)-Simplified is

very efficient when queries are known to be based

on relevant tags only, while A(k)-Relevant gives

good results when only the ending tags are known.

Performance examination shows that the indexes

give good results while increasing the number of

false drops by a very small proportion (and usually

do not increase false drops at all). We also offered a

method, based on partial order relation, to eliminate

false drops created by nodes removal, while

increasing the size of the index by no more then

1.5%.

More work is needed to modify existing indexes

for supporting irrelevant node’s removal. It seems

appropriate to adjust bisimulation based indexes to

support exploiting relevant set declaration, and

removing irrelevant nodes. Further work is needed

to make A(k)-Simplified and A(k)-Relevant support

DB functionality such as update, insert and delete.

ACKNOWLEDGEMENT

The Idea for A(k)-Relevant originated from

discussions with Philip Bohannon.

REFERENCES

Bray, T., Paoli, J., Sperberg-McQueen, C.M., Maler, E.

and Yergeau, F. (2004, February 2) "Extensible

Markup Language (XML) 1.0 (Third Edition), W3C

Recommendation", Available:

http://www.w3.org/TR/REC-xml.

Busse, R., Carey, M., Florescu, D., Kersten, M., Schmidt,

A., Mauolescu, I., and Waas, F. (2001, April) "The

XML Benchmark Project", Available:

http://monetdb.cwi.nl/xml/index.html.

Buneman, P., Davidson, S.B., Fernandez, M.F., and Suciu,

D. (1997) 'Adding Structure to Unstructured Data',

Proceedings of ICDT.

Li, Q. and Moon, B. (2001) 'Indexing and Querying XML

Data for Regular Path Expressions', Proceedings of

VLDB.

Derose, S., Maler, E. and Orchard, D. (2001, June 27)

"XML Linking Language (XLink), version 1.0, W3C

Recommendation", Available:

http://www.w3.org/tr/xlink.

Chamberlin, D., Florescu, D. and Robie, J. (2000) 'Quilt:

An XML Query Language for Heterogeneous Data

Sources', Proceedings of WebDB.

Figure 8: Query evaluation cost (on synthetic database). The left figure –

Relevant End queries. The right figure

– Relevant queries

0.00%

20.00%

40.00%

60.00%

80.00%

100.00%

012345678910

Percent of false drops

A(k)-Index A(k)-Simplified A(k)-Relevant A(k)-Simplified with False Drops Removal A(k)-Relevant with False Drops Removal

500

1,000

1,500

2,000

2,500

3,000

012345678910

Number of nodes scanned

500

1,000

1,500

2,000

2,500

3,000

012345678910

Number of nodes scanned

Figure 9: False drops in complex queries (on IMDB). The left figure – Relevant End queries. The right figure

– Relevant queries.

0.00%

10.00%

20.00%

30.00%

40.00%

50.00%

60.00%

70.00%

80.00%

90.00%

012345678910

Percent of false drops

0.00%

5.00%

10.00%

15.00%

20.00%

25.00%

30.00%

35.00%

012345678910

Percent of false drops

WEBIST 2005 - INTERNET COMPUTING

Abiteboul, S., Quass, D., McHugh, J., Widom, J. and

Wiener, J. (1997) 'The Lorel Query Language for

Semistructured Data', International Journal on Digital

Libraries, 1(1):68-88.

Clark, J. and Derose, S. (1999, November 16) "XML Path

Language (XPath) Version 1.0, W3C

Recommendation", Available:

http://www.w3.org/TR/xpath.

Deutsch, A., Fernandez, M., Florescu, D., Levy, A., and

Suciu, D. (1999) 'A Query Language for XML',

Proceedings of the Eighth World Wide Web

Conference.

Chamberlin, D., Florescu, D., Robie, J., Simeon, J.

and Stefanescu, M. (2005, February 11) " XQuery 1.0:

An XML Query Language, W3C Working Draft",

Available: http://www.w3.org/TR/xquery.

Schenkel, R., Theobald, A. and Weikum, G., (2004)

'HOPI: An Efficient Connection Index for Complex

XML Document Collections', Proceedings of EDBT.

Goldman, R. and Widom, J. (1997) 'Dataguides: Enabling

Query Formulation and Optimization in

Semistructured Databases', Proceedings of VLDB.

Goldman, R. and Widom, J. (1999) 'Approximate

DataGuides', Proceedings of the workshop on Query

Processing for Semistructured Data and Non-

Standard Data Formats, Pages 436-445.

Chung, C. W., Min, J. K. and Shim, K. (2002), 'APEX:An

Adaptive Path Index for XML Data', Proceedings of

SIGMOD.

Milo, T. and Suciu, D. (1999) 'Index Structures for Path

Expressions', Proceedings of ICDT.

Kaushik, R., Bohannon, P., Naughton, J.F. and Shenoy, P.

(2002) 'Updates for Structure Indexes', Proceedings of

VLDB.

Kaushik, R., Bohannon, P., Naughton, J.F. and Korth, H.F.

(2002) 'Covering Indexes for Branching Path Queries',

Proceedings of ACM SIGMOD.

Kaushik, R., Shenoy, P., Bohannon, P. and Gudes, E.

(2002) 'Exploiting Local Similarity for Efficient

Indexing of Paths in Graph Structured Data',

Proceedings of ICDE.

Qun, C., Lim A. and Ong, K. W. (2003) 'D(k)-Index: An

Adaptive Structural Summary for Graph-Structured

Data', Proceedings of ACM SIGMOD.

Papakonstantinou, Y., Garcia-Molina, H. and Widom, J.

(1995) 'Object Exchange Across Heterogeneous

Information Sources', Proceedings of ICDE.

Abiteboul, S. (1997) 'Query Semi-structured Data',

Proceedings of ICDT.

McHugh, J., Widom, J., Abiteboul, S., Luo, Q. and

Rajamaran, A. (1998) 'Indexing Semistructured Data',

Technical Report, Stanford University.

Henzinger, M., Henzinger, T. and Kopke, P. (1995)

'Computing Simulations on Finite and Infinite Graphs',

Proceedings of FOCS.

Milo, T. and Suciu, D. (1998) 'Optimizing Regular Path

Expressions Using Graph Schemas', Proceedings of

ICDE.

The Internet Movie Database Ltd, "Internet Movie

Database", Available: http://www.imdb.com.

Biber, P. and Gudes, E. (2005) 'Improving Algorithms for

Indexes in XML based Databases', Master's thesis,

The Open University of Israel.

USING RELEVANT SETS FOR OPTIMIZING XML INDEXES