XML-BASED EVALUATION OF SYNTHESIZED QUERIES

Ron G. McFadyen

, Yangjun Chen

, Fung-Yee Chan

Department of Applied Computer Science, University of Winnipeg,

515 Portage Avenue, Winnipeg, Manitoba, Canada, R3B 2E9

Supported by NSERC 105709-03 (139988) (Natural Sciences and Engineering Council of Canada)

Supported by NSERC 239074-01 (242523) (Natural Sciences and Engineering Council of Canada)

Keywords: XML, business rule, query tree, query evaluation

Abstract: XML repositories are a common means for storing documents that are available through Web technologies.

As the use of XML increases, there is a need to integrate XML repositories with other data sources to

supply XML-oriented applications. In this paper, we examine documents that express business rules in

XML format, and where the triggering and instantiation of rules requires execution of database queries. In

this way, an inference process is governed by an XML document tree that controls the synthesis and

evaluation of database queries.

1 INTRODUCTION

XML and related technologies are becoming a

dominant standard for storing, managing, and

exchanging information. In its basic application,

XML is used to semantically enhance web pages

through the use of user-defined tags. This

enhancement allows one to understand the context in

which data appears. For example, XML.org was

formed in 1999 and its web pages (

XML.org, 2005)

provide a portal to XML technologies for data

exchange purpose. At the time of writing, XML.org

lists focus areas that include Human Resources and

Printing & Publishing; other focus areas such as

Defense, Insurance, and Retail are planned. XML is

being adapted for use in many industries.

In this paper, we consider documents describing

requirements or rules to be met to achieve some

designation or status. As an example, consider a

university setting where specific requirements are

set out for students to receive a degree. Typically

these documents are found in university calendars

and are expressed in natural language as illustrated

in Figure 1. This sample document presents the

requirements for graduation for a 3-Year BSc in

Geography from some university. It can be used by a

student to guide the progress of his/her studies, a

graduation officer to determine if a student can

graduate, or by a university department to publish

established requirements.

An observation shows that when applying such

requirements to student histories, we can determine

those students who can graduate. This is essentially

a process deriving new information by making

inference based on rules and facts (Business Rules

Group 2000, Ross 1997). However, unlike a general

rule-based system, the inferences here can be

deduced only in the order implicit in a document

structure. For instance, to know whether a student

can graduate, we have to check whether the student

has earned at least the required 90 credit hours,

whether the residence requirement is satisfied, and

so on. Furthermore, to determine whether the

3-Year BSc (Geography)

Graduation Requirement

90 credit hours

Residence Requirement

Degree: minimum 30 credit hours

Major: minimum 18 credit hours

General Degree Requirement

Humanities: 12 credit hours

Science: 6 credit hours

Major Requirement

Minimum 30 credit hours

Maximum 48 credit hours

Required Courses

23.202 Intro Geography I

23.203 Intro Geography II

23.331 Advanced Geography

Choice

23.205 Atmos Sci or 23.206 Earth Sci

Figure 1: Graduation Requirements

G. McFadyen R., Chen Y. and Chan F. (2005).

XML-BASED EVALUATION OF SYNTHESIZED QUERIES.

In Proceedings of the First International Conference on Web Information Systems and Technologies, pages 24-31

DOI: 10.5220/0001232100240031

 SciTePress

residence requirement is satisfied, we must check

the number of degree credit hours and the number of

major credit hours. Obviously, it is an ordered

inference process.

In addition, during the process, a series of

queries must be evaluated and each query

corresponds to some inference step.

To handle the above problem, we introduce the

concept of synthesized query tree, which is an XML

document tree, to represent a set of queries that are

evaluated along a tree structure.

The remainder of this paper is organized as

follows. Next in section 2 we describe the system

architecture. In section 3 we describe the

requirements documents and in Section 4 we

introduce the boolean and general synthesized query

trees that are required to process the documents.

Section 5 presents a short conclusion and directions

for further work.

2 SYSTEM ARCHITECTURE

In Figure 2, we present a layered architecture for

processing student graduation requests.

In the architecture, the End-user Layer manages

the interaction with the end-user and relays requests

to the Application Layer which analyses a request

and activates appropriate rules. Rule processing may

require access to XML documents and to various

other data stores. This architecture is designed for

handling end-user requests and not for managing

workflow as in the XRML architecture discussed in

(Lee and Sohn, 2003).

The use case shown in Figure 3 illustrates how a

user uses the system to determine a specific

student’s graduation status. From this, we can see

that to handle the use case, the system needs to do

the following:

1. retrieve relevant student identification

information (see Figure 3, steps 3 and 4)

2. manage rule execution (see Figure 3, steps 5

and 6)

3. manage connections to other data sources such

as XML and student history (see Figure 3, steps 3,

4, 5, and 6)

All these are the main tasks of the application

layer. In fact the Application Layer is basically an

inference engine that derives knowledge using a rule

set represented in an XML document and data from

various data stores. The application layer

implements all the operations that will be discussed

in Sections 3 and 4.

From the above discussion, we can see that the

sample document can be considered as a rule set that

will be used to determine whether a student can

graduate with a specific major. Our model assumes

that querying some data store for ancillary

information is required, but in this paper we are

concerned only with query access and not updates to

these data.

3 REQUIREMENTS DOCUMENTS

In this section, we describe the document category

we are considering and specify how the document is

coded as an XML document. To the best of our

knowledge, this document category has not been

studied elsewhere.

We consider documents that describe

requirements to be met to achieve some designation

or status, as exemplified in Figure 1. The sample

document is typical of requirement specifications

that a student must meet in order to graduate with a

specific degree. As discussed previously, to

user request

result

Figure 2: Rule Processing Architecture

End-user Layer

Application Layer

Rule Processing

Students

Histories

XML

Documents

Use Case: Obtain Student Graduation Status

Main Success Scenario

1. Graduation officer selects the 3-Year BSc (Geography)

graduation requirements page to view

2. System presents graduation requirements page

3. Graduation officer selects a student

4. System retrieves and presents student information

5. Graduation officer requests student graduation status

6. System evaluates document rules using student

history data store and displays graduation status to user

Alternate Flows

5a) The student’s status relative to a specific

requirement in the document is requested

1. Graduation officer selects a specific requirement and

requests status relative to that requirement only

2. System evaluates the specific rule and displays status

Figure 3: Student Status Use Case

XML-BASED EVALUATION OF SYNTHESIZED QUERIES

determine if a student can graduate, an inference

process is required that must adhere to the order

implicit in the document structure.

The XML version of the sample document is

shown in Figure 4. Next we describe how this

document is established from the document shown

in Figure 1.

As we know, XML documents comprise

elements and attributes, which are marked up using

tags. Therefore, when we translate a plain text like

that in Figure 1 into an XML version, tags for

elements, as well as attributes have to be defined.

Especially, to model the inference process implied in

a requirements document, the following principles

should be followed.

1. Any requirement/sub-requirement relationship is

handled as an element/sub-element relationship

in XML.

2. For each element we define the attributes:

title: each element has a title for display

purposes.

display: each element may have additional text

for display purposes.

query: the query attribute holds a database query

that will be used to determine if the

corresponding requirement is satisfied for a

specific student. Only those elements that do not

have sub-elements, have a query attribute.

expected: the result expected from the query.

comparison: the operator to use to verify the

query result is the expected result.

combining: the combining attribute is a logic

operator “and” or “or” or a function call, which

indicates how sub-requirements are combined.

Only those elements that have sub-elements

have a combining attribute.

Figure 4: XML expression of graduation requirements

<GeographyRule title= “Degree Requirement for 3-Y

ear BSc

(Geography)”,

combining = ”AND” >

<GraduationRule title=”Graduation Requirement”,

display=”90 credit hours”, query= “...”, ...>

</GraduationRule>

<ResidenceRule title = ”Residence Requirement”,

combining = ”AND” >

<DegreeRule title = ”Degree Requirement”,

display = ”minimum 30 credit hours”,

query = ”SELECT sum(creditHours)

FROM studentHistory

WHERE

studentNumber=parameterValue”,

expected=”30”,

comparison= “>=” >

</DegreeRule>

<MajorRule title=”Major”, display=”minimum 18 credit hours”,

query=”... ”, ...>

</MajorRule>

</ResidenceRule>

<GeneralRule title=”General Degree Requirement,

combining = ”AND”>

<HumanitiesRule title=”Humanities”,

display=”12 credit hours”, query=”... ”, ...>

</HumanitiesRule>

<ScienceRule title=”Science”, display=”6 credit hours”,

query=”... “, ...>

</ScienceRule>

</GeneralRule>

<MajorRule> title=”Major Requirement”

combining = ”AND”>

<MinMaxRule

display=”Minimum 30 credit hours, Maximum 48 credit hours”,

query=”... “, ...>

</MinMaxRule>

<ReqCoursesRule title=”Required Courses” ,

combining = ”AND”>

<Course

display=”23.02 Intro Geography I”, query=”...”, ...>

</Course>

<Course

display=”23.203 Intro Geography II”, query=”...”, ...>

</Course>

<Course

display=”23.331 Advanced Geography”, query=”...”, ...>

</Course>

</ReqCoursesRule>

<ChoiceRule title=”Choice”,

display=”23.205 Atmos Sci or 23.206 Earth Sci”

combining = ”OR”>

</ChoiceRule>

</MajorRule>

</GeographyRule>

We give an example of the process to construct

an XML document. Consider the Residence

Requirement. This requirement has two sub-

requirements as shown in Figure 1. So we need a

Residence element and two sub-elements for Degree

and Major in its XML version. Furthermore, the

Residence element has a title with a value of

“Residence Requirement”, but does require any

further text to be displayed and so there is no value

for the display attribute. There is no query to execute

to determine if the Residence Requirement is

satisfied, rather it is necessary to determine if all

sub-requirements are satisfied. Therefore, there is no

value for the query attribute; queries will appear in

WEBIST 2005 - INTERNET COMPUTING

its sub-requirements. Lastly, since the Residence

Requirement has sub-requirements, the combining

attribute must be “and” since both sub-requirements

must be satisfied for the Residence Requirement to

be satisfied.

We continue this example one step further by

considering the Degree Sub-requirement. This

requirement does not have sub-requirements itself

and so we do not define any sub-elements of the

Degree element. The Degree element has a title with

a value of “Degree Requirement”, and requires a

value for the display attribute for the additional text

of “minimum 30 credit hours“. The Degree

Requirement needs a value for the query attribute so

that the minimum of 30 credits can be verified

against a database of student history information.

This query requires a parameter for the student

number since the student would not be known until

the query is executed. Note that the exact function or

query expression required here depends on the

database system being used. To pass the

requirement, the result must be at least 30 and so the

expected attribute is “30” and the comparison

operator is “>=“. Finally, since the Degree

Requirement has no sub-requirements, the

combining attribute is not given any value. The

above discussion leads to the following definitions

which appear in the XML document shown in

Figure 4.

Figure 4 can be viewed as a set of rules that

require evaluation to know the graduation status of a

student. Specifically, the rules will be evaluated in a

bottom-up way. That is, to know the value of any

rule, the value of its contained rules must be made

available first. In the next section, we discuss how

such a set of rules are evaluated.

4 SYNTHESIZED QUERY TREES

In this section, we describe the evaluation of the

rules represented in an XML document. For this

purpose, we introduce the concepts of synthesized

query trees, which are implemented in our system to

control the inference process. We distinguish two

kinds of synthesized query trees. One is the so called

boolean synthesized query tree, which will be

discussed in 4.1. The other is its extended version

for handling more complicated cases, and will be

discussed in 4.2.

4.1 Boolean Synthesized Query Tree

The documents discussed in Section 3 form a single

compound rule that comprises some other sub-rules.

The evaluation of such a rule requires either for all

of its sub-rules to be true, or, for at least one sub-rule

to be true. To control the evaluation of such a rule,

as well as the execution of the queries involved, we

present the Boolean Synthesized Query Tree as

follows.

Definition 1: a boolean synthesized query tree

(BSQT) is a tree where each leaf node v is associated

with a boolean query

()

, and each internal node v

is labelled with a tag T(v), and an operator

∨∧

; and each node v is assigned a

boolean value, V(v), determined as follows:

a) for a leaf node, V(v) is true if the return value

()

is not empty; otherwise, it is false, and

b) for an internal node, with children v

, ... v

()

()θ…θ

()

In Figure 5, we show a tree which is a BSQT,

derived from the XML document shown in Figure 4.

From this, we can see that the whole process of

evaluating the corresponding rule is explicitly

specified.

We also notice that in the BSQT an internal node

is either an and-node or an or-node according to the

operator used at that node. In addition, the value of

any node depends on the values of its descendants.

To determine the value of a node v, V(v), the value

of each descendant node must be determined first.

Therefore, the function V(v) is evaluated bottom-up.

For instance, the 3-Year BSc (Geography)

Requirement is satisfied if all of Graduation

Requirement, Residence Requirement, General

<ResidenceRule title = ”Residence Requirement”,

combining = ”AND” >

<DegreeRule title = ”Degree Requirement”,

display = ”minimum 30 credit hours”,

query = ”SELECT sum(creditHours)

FROM studentHistory

WHERE

studentNumber=parameterValue”,

expected=”30”,

comparison= “>=” >

</ResidenceRule>

</DegreeRule>

...

XML-BASED EVALUATION OF SYNTHESIZED QUERIES

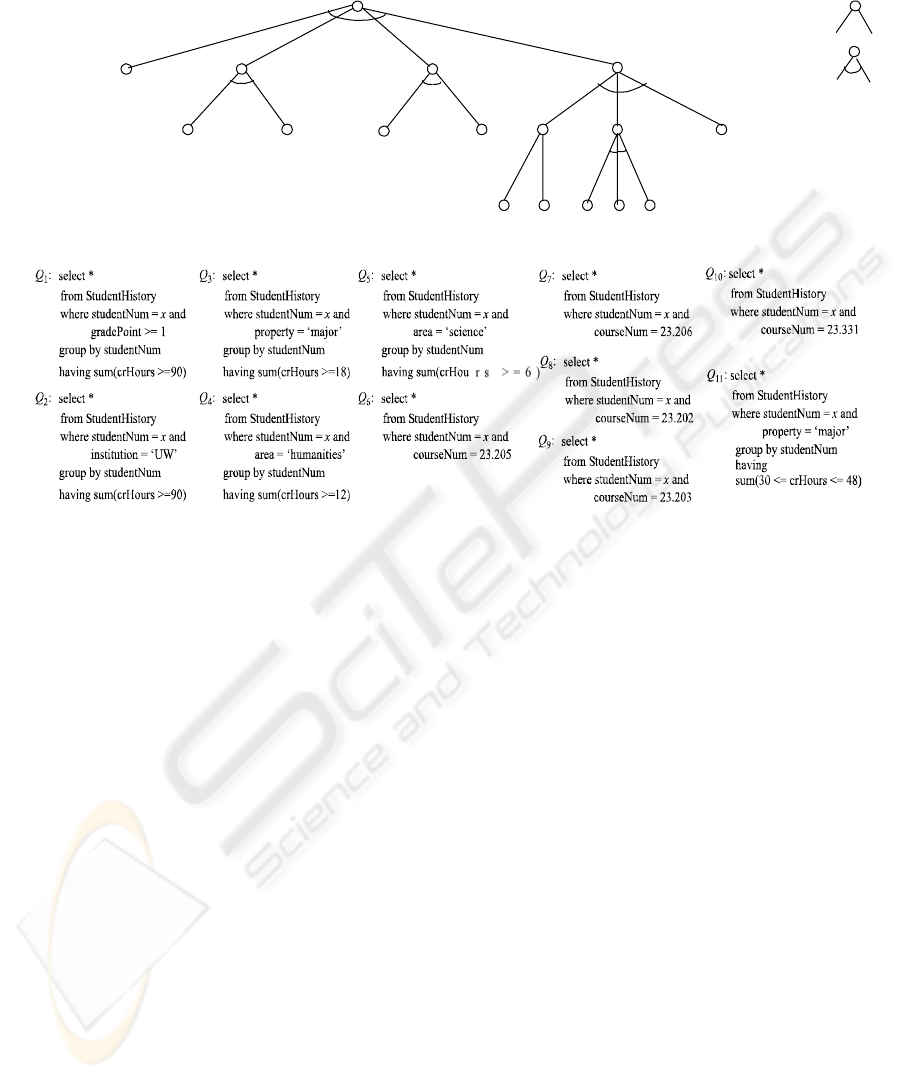
Requirement, and Major Requirement are satisfied.

Thus, the node labelled 3-Year BSc (Geography) is

an internal and-node representing a compound rule

where all sub-rules must be true for the requirement

to be satisfied. However, the node labelled Choice is

an internal or-node representing a choice a student

must make: to take one of two courses 23.205 or

23.206 (see Q

and Q

in Figure 5).

Of course, some rules do not have sub-rules; for

instance, the Degree Requirement specifies that the

student must have completed at least 30 credit hours

at the institution (see Q

in Figure 5). There is no

sub-rule this rule depends on; this rule requires the

evaluation of a query to determine if it is satisfied or

not. Degree Requirement is a leaf node in the BSQT.

A leaf node represents a simple requirement that

is not subdivided any further. In Figure 5, queries

are indicated for each leaf node. For instance, the

Graduation requirement is met if the student has at

least 90 credit hours in courses that have been

completed satisfactorily (a grade point of at least 1

in each course; see Q

in Figure 5). This can be

determined by querying an appropriate data store,

and the result is either true or false. For other leaf

nodes, similar queries would be specified. For the

purposes of this paper, we consider these queries are

explicitly coded, as they are typically done for

database applications.

Each node in the tree in Figure 5 expresses a

business rule for graduation. The tree is organized in

such a way that all data access is at leaf nodes and

each internal node organizes and accumulates the

results from its child nodes using logical and or or

operators.

When the graduation officer requests a student’s

graduation status for a degree, the graduation rules

must be evaluated bottom-up. This is accomplished

by the application layer performing a post-order

traversal of the tree. When leaf nodes are being

evaluated, a data store of student history information

must be accessed. Typically, this data store is a

relational database and SQL would be used by an

application layer to retrieve relevant information for

the officer to assess.

4.2 General Synthesized Query Tree

We now generalize our model to distributed

documents. In our exemplary requirements

document, there is a list of required courses for the

degree. Suppose the list of courses is not in this

XML document; rather, suppose the list of required

courses is stored in some data store and that the list

can only be retrieved in a query. This situation is one

where the list of required courses is maintained

separately from this XML document.

Residence

Degree

Major

General

Major

Required

Courses

Huma-

Science

Graduation

or-node:

Choice

3-Year BSc (Geography)

and-node:

Figure 5: A BSQT for graduation requirements

nities

MinMax

WEBIST 2005 - INTERNET COMPUTING

As we will discuss, this type of document

requires more expressive data manipulation, and so

we propose a more general query tree where a leaf

node may be single- or set-valued, and an internal

node may have operators other than and or or

associated with it. We define the general synthesized

query tree as below.

Definition 2: a general synthesized query tree

(GSQT) is a tree where each leaf node v is associated

with a query Q(v), which returns a value or a set of

values, and each internal node v is labelled with a

tag T(v), a function f, and each node will be assigned

a value V(v), as follows:

a) for a leaf node, its value V(v) is equal to the

return value of

()

, i.e.,

()

, and

b) for an internal node, with children v

, ... v

()

()…

(),,,()

In Figure 6, the same requirements as before are

illustrated, but we imply that the set of required

courses is obtained using a query submitted against

some data store. Here, we assume that external data

can be obtained from any available or required data

store.

Now, given that the required courses for the 3-

Year BSc (Geography) are kept elsewhere, to

determine if a student has successfully passed all

courses, the process of evaluating the requirement

has to be carried out differently from before. To

evaluate the requirement, the graduation officer must

run two queries and combine their results as we

explain next.

First, a list of courses successfully passed by the

student is obtained. Let us name this result

SuccessResult and assume this result is a relation

with two attributes: student number and course

number. Since we are considering a single student,

the same student number will appear in each tuple.

The other list obtained is a list of required courses.

Let us name this result RequiredList and assume this

result is a relation with one attribute: course number.

Note these two relations have one common attribute:

course number. The graduation officer needs to

determine if the set of courses successfully passed

includes the set of required courses. To do this, the

relational algebra division operator (Elmasri and

Navathe, 2003) should be conducted:

SuccessResult[studentNum, courseNum]

RequiredList[courseNum].

The result of this operation is a relation of one

attribute: student number. In the result, a student

number appears if the student number appears in

SuccessResult with some course numbers which

form a super-set of RequiredList. In our example, if

the student has successfully taken each required

course, then the result of division is a relation of one

tuple having the student number of that student. If

the student has not taken all of the required courses

then our result is a relation of zero tuples - an empty

relation. The division operator is difficult to explain.

It is even more difficult to express in the standard

relational language SQL and error-prone since it is

not directly supported in that language. For this

reason, the document designer may prefer a different

approach where division is directly supported. We

note that the division can be expressed simply, as

shown in Figure 6.

In Figure 7, we illustrate a subtree rooted at

Major in the GSQT for our running example, for

which various functions are required to manipulate

the values obtained from descendant nodes in the

GSQT. For instance, associated with v

, we have a

division operation while for v

, the operation is the

projection.

In the Figure, the functions f( ) and g( ) are

defined as follows:

f(x, y): if x

∈ y, returns true; otherwise, false.

g(x): if 30

≤ x ≤ 48, returns true; otherwise, false.

As with the other operations, they take the values

from the corresponding child nodes as the

parameters. We also note that each leaf node in the

tree is associated with a query, which provides the

initial values for computation. Therefore, the

evaluation of V(v) for any node is performed

bottom-up. For instance, the value of v

, V(v

), is

calculated by dividing the result of Q(v

) through

the result of Q(v

) (i.e., Q(v

) ÷ Q(v

); both of

them come from its children); V(v

) is obtained by

computing g(V(v

)), and so on.

The GSQT is similar to the concept of query

trees used for constructing query execution plans in

relational database systems (Elmasri and Navathe,

2003). We note that, however, our documents have a

number of queries and for the purpose of evaluating

sub-rules separately, it is necessary for each sub-rule

to be self contained and for its query requirement to

be expressed independently of other rules.

select all

required courses

select all

courses taken

by student s

= Q

divide Q

from external source

Figure 6: Division operation

XML-BASED EVALUATION OF SYNTHESIZED QUERIES

Furthermore, for queries in our example, several

queries access the same data and some query results

can even be derived from other queries, which

cannot be expressed in any kind of query trees.

(Finally, if this knowledge is exploited during

document/query processing, it is possible for us to

realize efficient query processing.)

In (Bonifati, Ceri and Paraboschi 2001,

Abiteboul, Benjelloun, Manolescu, Milo, and Weber

2002), distributed XML documents are considered.

In these, document queries are used to retrieve

distributed portions of an XML document. The

queries and documents in (Bonifati et al 2001,

Abiteboul et al 2002) are not the same as the

situation here since in our model the queries we are

considering are used to retrieve data from (for

example) SQL database systems.

5 CONCLUSION AND FUTURE

WORK

In this paper, we consider a kind of document, the so

called requirements document. Each document can

be considered as a single compound rule. When such

a document (e.g. BSc Graduation Requirement) is

evaluated in a certain context (e.g. for a specific

student) there will be a value generated for it. In our

example, the value generated for the document is the

graduation status for a particular student. For this

type of document, the BSQT and GSQT succinctly

represent the document evaluation and query

requirements; a simple tree traversal is required to

evaluate a document.

The BSQT and the GSQT structures can be

applied to any part of a document, and the BSQT

and GSQT could appear in multiple places of a

document. For example, the General Calendar

published by a university would have many GSQTs,

one for each degree program for each department.

We are currently developing a prototype system

which requires a complete specification of rule

processing, synthesized tree instantiation, and

connection to a database system. Concurrently, we

intend to examine other issues related to the

processing of these types of query-based documents,

such as rule markup, event-condition-action model,

Document Object Model, query optimization,

workflow, active XML documents, and

composing/assembling documents from other

documents. For example, the event-condition-action

model for rule processing can be incorporated if we

take into account the updates to the Student History

Data Store. At the end of term, when marks for a

student have been entered, the graduation

requirements document/rule processing can be

activated. As another example, a university may

offer a double major program that can be

represented as a composite requirements document

defined and assembled from existing documents.

REFERENCES

Abiteboul, S., Benjelloun, O., Manolescu I., Milo, T.,

Weber, R., 2002. Active XML: peer-to-peer data and

web services integration (demo), in Proceedings of

VLDB.

Major

Select sum(cr hrs)

Figure 7: Graduation requirements as a GSQT

select all

required courses

select all

courses taken

by student x

Q(v

) ÷ Q(v

)

select *

where course taken

is 23.205 or 23.206

by student x

from ...

from external source

V(v

) =

Q(v

):Q(

V(v

) = π

STUDENT NUM

(V(v

)) V(v

) = π

STUDENT NUM

(V(v

))

V(v

) = π

SUM

(V(v

))

V(v

) = V(v

) ∧ V(v

)

V(v

) = f(x, V(v

))

V(v

) = f(x, V(v

))

V(v

) = g(V(v

))

WEBIST 2005 - INTERNET COMPUTING

Bonifati, A., Ceri, S. and Paraboschi, S., 2001. Active

rules for XML: A new paradigm for E-services, in

VLDB Journal, 10, 39-47.

Business Rules Group, July 2000. Defining business rules:

What are they really?, 3

edition,

http://www.businessrulesgroup.org.

Elmasri, R. and Navathe, S. B., 2003. Fundamentals of

database systems, Addison-Wesley, 4

edition, ISBN

0321122267.

Lee, J. K. and Sohn, M. M., May 2003. The extensible

rule markup language, in Communications of the

ACM, 46(5).

Ross, R. G., 1997. The business rule book, Business Rule

Solutions, Houston, 2

edition, ISBN 0941049035.

XML.org, retrieved January 2005, from http://XML.org

XML-BASED EVALUATION OF SYNTHESIZED QUERIES