SECRET LOCKING: EXPLORING NEW APPROACHES TO

BIOMETRIC KEY ENCAPSULATION

Seny Kamara

Johns Hopkins University

Department of Computer Science

3400 N Charles Street, Baltimore, MD 21218, USA

Breno de Medeiros

Florida State University

Department of Computer Science

Tallahassee, FL 32306-4530, USA

Susanne Wetzel

Stevens Institute of Technology

Department of Computer Science

Castle Point on Hudson, Hoboken, NJ 07030, USA

Keywords:

Biometrics, secret sharing, secret locking, error-tolerance.

Abstract:

Biometrics play an increasingly important role in the context of access control techniques as they promise to

overcome the problems of forgotten passwords or passwords that can be guessed easily.

In this paper we introduce and provide a formal deﬁnition of the notion of secret locking which generalizes

a previously introduced concept for cryptographic key extraction from biometrics. We give details on an

optimized implementation of the scheme which show that its performance allows the system for use in practice.

In addition, we introduce an extended framework to analyze the security of the scheme.

1 INTRODUCTION

Biometrics play an increasingly important role in a

broad range of security applications. In particular,

biometrics have manifold applications in the context

of access control techniques which to date are largely

based on the use of passwords. Biometrics promise

to overcome the problems of forgotten passwords or

passwords that can be guessed easily.

Most biometric systems used in practice to date

store proﬁles of users. A user proﬁle typically consists

of a collection of measurements of the user’s physi-

cal characteristics (e.g., the user’s iris patterns or ﬁn-

gerprints) obtained during an initial enrollment phase.

Later, when a user presents herself for identiﬁca-

tion, the system performs measurements and matches

those against the database of stored user proﬁles. If a

“good” match is found, the user is identiﬁed. While

these systems protect against an online attacker, they

however, pose a considerable risk for ofﬂine attacks in

which an attacker may obtain and exploit the knowl-

edge of the stored proﬁles.

Recently, the alternative approach of biometric key

encapsulation has been proposed: instead of replac-

ing the use of passwords by means of biometrics,

passwords are “hardened” by incorporating biomet-

ric features. No user proﬁles are stored in the sys-

tem. Due to the inherent variability in biometric read-

ings, the system, however, requires a biometric fea-

ture extractor in order to reliably recover the same

(cryptographic) key from an imprecise input, i.e., to

provide “error tolerance.” In this context, a solution

based on error-correcting codes and randomness ex-

traction was developed (Juels and Wattenberg, 1999;

Juels and Sudan, 2002; Dodis et al., 2004; Boyen,

2004). An alternative line of work based on secret

sharing techniques was proposed in (Monrose et al.,

2002; Monrose et al., 2001). While the former pro-

vides an information-theoretical optimal solution for

error-tolerance, it at the same time requires a uniform

level of error-tolerance for all users alike and as such

poses signiﬁcant challenges for use in practice. In

254

Kamara S., de Medeiros B. and Wetzel S. (2005).

SECRET LOCKING: EXPLORING NEW APPROACHES TO BIOMETRIC KEY ENCAPSULATION.

In Proceedings of the Second International Conference on e-Business and Telecommunication Networks, pages 254-261

DOI: 10.5220/0001408002540261

 SciTePress

contrast, the latter allows for an individual level of

error-tolerance for each user.

In this paper we focus on extending the work in

(Monrose et al., 2002). In particular, we introduce

a formal deﬁnition of the notion of secret locking

which generalizes the concept proposed previously.

We furthermore provide an extended discussion on

the determinant-based scheme. We give details on an

optimized implementation of the scheme which show

that its performance allows the system for use in prac-

tice. In addition, we introduce an extended framework

to analyze the security of the scheme. In the original

work, the security of the determinant-based construc-

tion was proved under an idealized attack model only.

In this paper we consider arbitrary attacks. Finally,

we discuss heuristic connections between the security

of the scheme and well-known hard problems in com-

putational mathematics and coding theory.

1.1 Motivation

Using biometrics in practice poses a number of chal-

lenges, in particular when used in applications to pro-

tect resource limited devices such as cell phones or

PDAs. Ideally, these devices should obtain biometric

measurements without requiring any additional ded-

icated hardware. Currently, most portable devices

have built-in microphones, keyboards or writing pads.

As such, systems using biometrics such as voice pat-

terns, keystroke dynamics or stylus drawing patterns

are more readily deployable than systems based on

iris or retina scans. Furthermore, it should be difﬁ-

cult for an adversary to capture the user’s biometric

measurements, and in particular this counter-indicates

ﬁngerprint scans as a biometric in this regard, as ﬁn-

gerprint marks are quite easy to obtain.

Static vs. Non-static Biometrics. While static bio-

metrics capture physiological characteristics of an in-

dividual (e.g., iris or retina patterns, and ﬁngerprints),

non-static biometrics (e.g., voice patterns, keystroke

dynamics) relate to behavioral characteristics. In gen-

eral, it is harder for an attacker to capture non-static

than static biometrics, so they could prove useful for

the type of application we consider. However, non-

static biometrics have a high variability of robust-

ness from user to user: Some users have more reli-

ably reproducible feature readings than others. Con-

sequently, less error-tolerance is required to support

identiﬁcation of users with more reliably reproducible

feature readings (Doddington et al., 1998).

Biometric Key Encapsulation requires the exact

reconstruction of the underlying key, and some form

of error-tolerance must therefore be employed in or-

der to accommodate the variability in biometric read-

ings. In order for a system to accommodate different

levels of error-tolerance allowed to identify particu-

lar users, ideally it should allow for variable error-

tolerance. Alternatively, the system-wide level could

be adjusted to the worst case, i.e., the least robust

user. In (Juels and Wattenberg, 1999; Juels and Su-

dan, 2002; Dodis et al., 2004; Boyen, 2004) error-

tolerance is achieved by means of error-correcting

codes and randomness extraction. In practice, this so-

lution either requires uniformity, with the same error-

correcting code employed for all users, or the codes

need to be deﬁned on a user-by-user basis. While the

former solution suffers from the problem that the se-

curity of the system is reduced to the level of the least

robust user, the latter reveals to an attacker the code

used (and therefore the level of error-tolerance sup-

ported) upon inspection.

In contrast, the system introduced by Monrose et

al. allows for non-uniformity of robustness of a user’s

biometric characteristics. In particular, the system

hides the amount of error-tolerance required by a spe-

ciﬁc user. In other words, if the attacker has access

to the key encapsulation value, his effort to decide

how much error-tolerance the particular user required

should be roughly equal to the effort of breaking the

key encapsulation of that user.

2 RELATED WORK

There are numerous approaches described in liter-

ature to use biometrics for authentication purposes

or to extract cryptographic secrets from biometrics.

There are various systems using biometric informa-

tion during user login process (e.g., (Joyce and Gupta,

1990)). These schemes are characterized by the fact

that a model is stored in the system (e.g., of user

keystroke behavior). Upon login, the biometric mea-

surements (e.g., user keystroke behavior upon pass-

word entry) are then compared to this model. Since

these models can leak additional information, the ma-

jor drawback of these systems is that they do not pro-

vide increased security against ofﬂine attackers.

In (Soutar and Tomko, 1996), a technique is pro-

posed for the generation of a repeatable cryptographic

key from a ﬁngerprint using optical computing and

image processing techniques. In (Ellison et al., 2000),

cryptographic keys are generated based on users’ an-

swers to a set of questions; subsequently, this sys-

tem was shown to be insecure (Bleichenbacher and

Nguyen, 2000). Davida, Frankel, and Matt (Davida

et al., 1998) propose a scheme which makes use of

error-correction and one-way hash functions. The for-

mer allows the system to tolerate a limited number of

errors in the biometric reading. This approach was

generalized and improved in (Juels and Wattenberg,

SECRET LOCKING: EXPLORING NEW APPROACHES TO BIOMETRIC KEY ENCAPSULATION

255

1999) by modifying the use of error-correcting codes.

In (Monrose et al., 2002; Monrose et al., 2001),

a new approach is proposed, focusing on using key-

stroke features and voice characteristics to harden the

passwords themselves. The work improves on previ-

ous schemes in that it is the ﬁrst to offer better se-

curity against a stronger attacker. Furthermore, this

approach allows a user to reconstruct the key even if

she is inconsistent on a majority of her features. The

techniques introduced by (Ellison et al., 2000; Davida

et al., 1998; Juels and Wattenberg, 1999) respectively,

do not permit that.

Recently, a new theoretical model for extracting

biometric secrets has been developed (Juels and Su-

dan, 2002; Dodis et al., 2004; Boyen, 2004), extend-

ing the work in (Juels and Wattenberg, 1999). The

model is based on the use of population-wide met-

rics combined with (optimal) error-correction strate-

gies. While the model is provably secure and allows

for optimal constructions under certain assumptions,

it has not been empirically validated that these con-

structions are applicable to biometrics of interest in

practice.

3 SECRET LOCKING AND

SECRET SHARING SCHEMES

In the traditional setting, a secret sharing scheme

consists of a dealer, a set of participants P =

, . . . , P

}, an access structure Γ ⊆ 2

as well

as algorithms Share and Recover. In order to share

a secret s amongst the participants, the dealer uses

the algorithm Share to compute each share s

to send

to user P

. In order to reconstruct the shared se-

cret using the algorithm Recover, only those shares

are needed which correspond to authorized subsets

of participants —i.e., shares corresponding to sets in

the access structure Γ. The most well-known secret

sharing schemes are threshold schemes. While these

schemes have a simple access structure (which con-

tains all user sets of cardinality larger than a threshold

t, i.e., S ∈ Γ ⇐⇒ |S| > t), for use with biomet-

rics, we are interested in secret sharing schemes with

different properties.

The concept of a compartmented access structure

was introduced in (Simmons, 1990), and has re-

ceived attention from a number of researchers (Brick-

ell, 1989; Ghodosi et al., 1998). In a compartmented

secret sharing scheme, each user P

is assigned a level

ℓ(P

). The same level may be assigned to different

users. In order to reconstruct the secret, one share

from each level is needed. More formally, the ac-

cess structure of the compartmented secret sharing

scheme is Γ = {A ∈ 2

: A ∩ P

6= ∅}, where

= {P

∈ P : ℓ(P

) = i}.

Compartmented access structures can be used to

achieve error-tolerance in biometric key encapsula-

tion: Let φ = (φ

)

i=1,...,m

be the set of discretized

measurements

of biometric features (for instance

timing intervals between different keystrokes). Each

assumes a value in the same ﬁnite set D. For

each user U , let R

(U) ⊂ D be the range of val-

ues that are likely

to be observed by measuring φ

on user U. In order to encapsulate a key u for user U,

where the key is a random value from a ﬁnite ﬁeld F

proceed as follows. First, deﬁne a virtual participant

set P = {P

i,j

}

{i=1,...,m;j∈D}

, and assign to P

i,j

level ℓ(P

i,j

) = i. Next, use the Share algorithm for

the compartmented access structure to compute initial

shares s

′

i,j

. Finally, perturb this initial set of shares to

obtain shares s

i,j

which match the initial shares s

′

i,j

whenever j ∈ R

(U), and are set to a newly chosen

random share value otherwise. When the legitimate

user U presents herself for authentication, it is sufﬁ-

cient to measure each value φ

(U) ∈ D of the biomet-

ric feature φ

on user U, then select the share s

i,φ

(U)

from level i and apply the Recover algorithm. By

construction, the outcome is likely to be the encap-

sulated secret u. On the other hand, the same is not

likely to be the case if a different user U

′

tries to im-

personate U, as the feature values for U

′

are not likely

to align (i.e., fall in the likely range at each level) with

those of U.

The above idea can be readily applied with any ef-

ﬁcient compartmented secret sharing scheme, such

as that in (Ghodosi et al., 1998), if the target is

simply user authentication. However, as we seek

mechanisms to achieve secure key encapsulation, the

scheme must moreover have the property that an at-

tacker who has access to the set of all shares cannot

determine which shares to pick at each level. It can be

readily seen that the scheme in (Ghodosi et al., 1998)

is not secure in this sense, and therefore is not sufﬁ-

cient for our purposes.

We can abstract the previously introduced concepts

as follows: Let D be a ﬁnite set, and consider the

product set D

. We call an element (φ

)

i=1,...,m

∈

a sequence of feature values. Consider some uni-

verse U, and for each element U of the universe, and

for each feature value φ

we associate the likely range,

a subset R

(U) ⊂ D. Let ρ

= R

(U)/D be the rel-

ative size of the likely range R

(U). Let τ

(U) be

deﬁned as − log(ρ

), which equals the logarithm of

Biometric measurements are continuous values. Mea-

surements are discretized by breaking the range of the mea-

surement into equal probability ranges.

One needs repeated measurements of each biometric

feature in order to arrive at the range of likely values. Par-

ticularly with non-static biometrics this range may vary over

time. Refer to (Monrose et al., 2002) for details of a practi-

cal implementation of such a scheme.

ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS

256

the expected number of random trials before a value

for φ

(U) is chosen within U’s likely range R

(U),

among all values in D. Finally, let τ

(U).

The value τ

is the logarithm of the expected num-

ber of random trials before one produces a sequence

of likely features (for U ) by simply choosing random

sequences in D

. Clearly, τ

is a natural parameter

of the difﬁculty of guessing likely sequences for U.

Deﬁnition 1 A secure secret locking scheme is a set

of algorithms Share and Recover with the following

properties:

1. Given a compartmented participant set P =

i,j

}

{i=1,...,m;j∈D}

, where D is a ﬁnite set, and

given a secret s in F

, Share produces a collection

i,j

of shares (which are values in a set S) which

implement the access structure Γ = {A ∈ 2

: A∩

6= ∅, i = 1, . . . , m}, where P

= {P

i,j

}

j∈D

In other words, Share and Recover implement a

compartmented secret sharing scheme with levels

i = 1, . . . , m.

2. Assume that a set of shares s

i,j

originally produced

by Share has been perturbed by substituting for

i,j

a random element of S whenever j is not a

likely value for φ

(U). Then, each probabilistic al-

gorithm A, that receives as input the share set (par-

tially randomized as above), and that terminates in

polynomially many steps in τ

has negligible prob-

ability of success in recovering the original shared

secret.

Binary Features: In the following we describe some

general constructions of the secret locking concept in-

troduced in (Monrose et al., 2002). For simplicity of

argument, we assume that all features assume binary

values, i.e., D = {0, 1}, even though all schemes de-

scribed can be generalized to any ﬁnite D. In the bi-

nary case, the range of values R

(U) for a feature i

and element U is one of three possibilities, namely

{0}, {1}, or {0, 1}. In the latter we call the fea-

ture non-distinguishing for U , while in the former two

cases the feature is distinguishing.

3.1 Secret Locking Constructions

For each construction, it is sufﬁcient to provide the

algorithms Share and Recover, as the security prop-

erty is not constructive. Instead it must be veriﬁed for

each construction. We ﬁrst describe an implementa-

tion of secret locking introduced in (Monrose et al.,

2002) which is based on the well-known Shamir se-

cret sharing scheme:

Shamir Secret Sharing (SSS) is based on polyno-

mial interpolation. In general, for a random poly-

nomial f(x) over Z

of degree d − 1 and a secret

K = f(0) ∈ Z

to be shared, a share will be deter-

mined as a point on the polynomial, i.e., as the tuple

(x, f(x)). Using Lagrange interpolation, the knowl-

edge of at least d distinct shares will allow the recon-

struction of the secret K (Shamir, 1979).

In order to construct a secret locking scheme based

on SSS, it is sufﬁcient to choose f(x) as a polyno-

mial of degree m − 1 with f(0) = K. The 2m

shares {s

, s

}

1≤i≤m

of secret K are determined as

= f(2i) and s

= f(2i + 1). Consequently, any

m shares will allow for the reconstruction of the se-

cret K, and clearly one share per row will do. How-

ever, this scheme is not compartmented, but simply

a threshold scheme. Furthermore, it does not pro-

vide security in the sense of our deﬁnition if the per-

centage of distinguishing features is small (i.e., less

than 60% of the total number of features). This is

due to the fact that it is then possible to treat the sys-

tem as a Reed-Solomon list decoding problem, which

can be solved by means of a polynomial time algo-

rithms (Guruswami and Sudan, 1998).

A truly compartmented construction based on

unimodular matrix constructions is also presented

in (Monrose et al., 2002), and is the focus of our at-

tention for the remaining part of the paper.

Determinant-based Secret Locking Construction.

The determinant-based scheme introduced in (Mon-

rose et al., 2002) encapsulates a secret by means of a

set of vectors in a vector space. In general, for a se-

cret K ∈ Z

to be shared, the shares are determined

as vectors in Z

. The secret can be reconstructed by

arranging m of the shares in an m × m-dimensional

matrix and computing its determinant.

In order to construct the set of shares, initially m

vectors s

in Z

are chosen with the property that

det(s

, . . . , s

) mod p = K, the secret to be encap-

sulated. The second set of shares is then determined

by means of a unimodular transformation matrix U =

, . . . , u

) where u

∈ Z

(1 ≤ i ≤ m). The uni-

modular matrix can be efﬁciently generated by per-

muting the rows of a random, triangular unimodular

matrix: U = Π·U

′

·Π

−1

, where Π = (π

, . . . , π

) is

any permutation matrix and U

′

= (u

′

, . . . , u

′

) is an

upper-triangular matrix that has 1 for each diagonal

element and random elements of Z

above the diago-

nal. Eventually, the second set of shares is computed

as s

= Us

for 1 ≤ i ≤ m.

It can be easily seen from the way the shares are

constructed, that this scheme indeed implements a

compartmented access structure. In fact, if one share

is picked from each one of the m levels (feature),

the secret K can be reconstructed —due to the uni-

modular relation between the two shares at the same

level. However, if the two shares from the same level

are used, then the reconstructed secret is random, as

SECRET LOCKING: EXPLORING NEW APPROACHES TO BIOMETRIC KEY ENCAPSULATION

257

the unimodular relationship between the two sets of

shares is not preserved. In the following sections, we

discuss the security characteristics of this scheme, and

provide details on an optimized implementation of the

scheme with good performance proﬁle.

3.2 Security

In this section we explore some of the underlying

hard problems that are related to the security of the

determinant-based sharing scheme described above.

Note that while the construction and its analysis are

presented only for the case of binary features, similar

arguments can be presented for the general case.

First, consider the case when all features are dis-

tinguishing, and thus only one sequence of feature

values reveals the secret. By construction, all other

shares are random and cannot be combined with the

true shares to obtain any partial information about the

secret. Moreover, without further information (such

as cipher-text encrypted under the encapsulated key)

the attacker cannot distinguish when the correct secret

is reconstructed. The probability of success is there-

fore 2

−m

, where m is the total number of features.

In the presence of non-distinguishing features the

setting is different. For instance, consider the case

where the ﬁrst feature is non-distinguishing. Let φ

and φ

be two feature sequences that differ only in

the ﬁrst feature, with φ

= 0 and φ

= 1. Sup-

pose further that both feature sequences are valid

for U, i.e., lead to reconstruction of the correct se-

cret. That means that the following matrices have the

same determinant: K = det



· · · s



det



· · · s



, where φ

= φ

for i > 1. It is well-known that the determi-

nant is a multi-linear function of the matrix columns,

which implies: det



− s

· · · s



= 0

mod p. We conclude that if the ﬁrst feature is non-

distinguishing one ﬁnds a non-trivial algebraic rela-

tion on the sets of shares. The method is not construc-

tive, however, because it requires previous knowledge

of a valid sequence of values for all the other features.

In order to search for such relations systematically,

one represents the choice for the value of feature i

as a function of a boolean variable, φ

) = if x

then s

i,1

else s

i,0

. The determinant computation

may then be fully expanded as a boolean circuit, and

the equation which expresses the determinant being

equal to 0 mod p reduced to a single boolean for-

mula. Any satisfying assignment to that formula cor-

responds to a sequence of feature values which may

be a valid sequence for U , and conversely all valid

sequences for U give rise to satisfying assignments.

Since SAT approximation algorithms can generally

only handle relatively small boolean formulas (in the

thousands of variables), the complexity of this ap-

proach can be estimated by studying a relaxation of

the problem. In order to “linearize” the boolean for-

mula, we allow feature choices in the whole ﬁeld F

by putting φ

) = (1 − x

i,0

+ x

i,1

. Note that

(0) = s

i,0

and φ

(1) = s

i,1

correspond to legiti-

mate shares, while for other values in x

∈ F

there

is no natural interpretation to the meaning of φ

Linearization enables the use of the rich machinery

of computational algebra to attack the corresponding

“relaxed” problem of ﬁnding zeros of the multilin-

ear polynomial ∆(x

, . . . , x

) which represents the

determinant det(s

− s

, (1 − x

+ x

, · · · ,

(1 − x

+ x

n = 5 6

(2, 100, 25, 30.6) (2, 60, 49, 60.25)

7 8

(2, 80, 97, 120.6) (3, 60, 225, 252.3)

9 10

(3, 40, 449, 502.6) (4, 10, 961, 1017.7)

Figure 1: n = # of features. The quadruplet under n = 6

indicates that the # of distinguishing features was 2, and

∆ had a minimum of 49 and an average of 60.25 non-zero

coefﬁcients over 60 random trials.

The complexity of this zero-ﬁnding problem was

assessed by means of experiments using the symbolic

computation package MAPLE. In particular, the ex-

periments determined the number of non-zero coef-

ﬁcients of ∆(x

, . . . , x

), for 5 ≤ n ≤ 10. It was

assumed that only ⌊0.4n⌋ of the features were distin-

guishing —a conservative approach, since the fewer

distinguishing features there are, the more symmetric

the polynomial should be, and the greater the chances

are that some of its coefﬁcients evaluate to 0. The

results or the experiments are shown in Fig. 1. These

results support the security of the scheme, as the num-

ber of non-zero coefﬁcients exhibits an exponential

increase. As a consequence, this renders any alge-

braic attempts to attack the problem ineffective, and in

fact, even the best approximation algorithms known

to date to simply counting zeros (as opposed to ﬁnd-

ing them) on multilinear polynomials have linear cost

with the number of non-zero coefﬁcients (Karpinski

and Lhotzky, 1991).

4 IMPLEMENTATION

In order to implement the scheme in practice, it is not

sufﬁcient to have error-tolerance purely from the se-

cret sharing construction, as features φ

will occasion-

ally assume a value outside the likely range R

(U)

even if evaluated on the legitimate user U. We call

ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS

258

128 112 96 82 64 48 32 16

Time (s)

Matrix size

Gauss

Gauss-Bareiss

Figure 2: Time to compute determinants as a function of the matrix size. The times are averaged over 10000 runs.

such errors “noisy errors.” Unlike the natural varia-

tion of measurements within likely ranges, the vari-

ability introduced by noisy errors is not tolerated well

by the secret locking construction. In practice, we

can accommodate a few of these errors by simply ex-

ecuting an exhaustive search on a Hamming ball of

small radius d centered on the measured input se-

quence φ = (φ

(U))

i=1,...,m

. We show that with ap-

propriate optimizations, this method is practical for

small values of d, for instance d ≤ 3, which seems

more than sufﬁcient to guarantee a reasonable false

negative rate with keyboard typing patterns (Monrose

et al., 2002).

The ﬁrst optimization we made was to change the

mechanism for reconstructing the secret from the se-

lected matrix entries. Instead of insisting on sharing

the determinant —which would require working with

matrices over large ﬁnite ﬁelds F

, with log q ≥ 80

—we instead use a hash function such as SHA-1 to

process the concatenation of all matrix entries from

the distinguishing features. Recall from Section 3.2

that once a feature sequence is found with the cor-

rect values for all distinguishing features, the non-

distinguishing positions can be detected by showing

that the determinant remains unchanged if that fea-

ture value is ﬂipped. Using this modiﬁed recovery al-

gorithm we can allow the dimension of the base ﬁeld

to be made much smaller, without affecting the en-

tropy of the keyspace. In our experiments we used

= Z

8191

, which allows each matrix entry to ﬁt in

a 16-bit buffer. This also enables implementation of

all modular and matrix operations using native 32-bit

integer operations and optimized C code.

Experimental Setup. All the experiments were

conducted on a 64-bit dual 2 GHz PowerPC G5 run-

ning MacOS Server 10.3.5, with 3 GB main mem-

ory, and 4 KB virtual pages. Our implementa-

tion is in C and compiled with gcc 3.3 using the

-O3, -ffast-math, -malign-natural and

-fprefetch-loop-arrays optimization ﬂags.

(For more details on gcc optimizations see (The

GNU Project, 2005).) We note that the Apple G5 pro-

vides native support for 32-bit applications and that

all our code was compiled for a 32-bit architecture.

All arithmetic is performed in Z

∗

, where p is prime

and equals 8191 = 2

− 1. Since we are working

on a 32-bit architecture and 8191 < 2

, all elements

in Z

∗

8191

can be stored in shorts. This means that

multiplication in Z

∗

8191

will not overﬂow the size of

a regular int and that we can implement the scheme

without multi-precision arithmetic.

Computing Determinants. Given feature sequence

′

, we begin by generating all sequences within a

hamming distance e of φ

′

. We call this set β(φ

′

, e) =

{φ

∗

∈ {0, 1}

: dist(φ

∗

, φ

′

) ≤ e}. For each φ

∗

∈

β(φ

′

, e), we then compute K

′

= det(s

∗

· · · s

∗

)

and check whether K

′

= K. Since |β(φ

′

, e)| =

i=0





, we have to perform a large number of

determinant computations, and therefore it is impor-

tant to optimize the running time of determinant eval-

uation. We ﬁrst benchmarked the performance of

various determinant algorithms and implementations,

in particular Gaussian elimination and Gauss-Bareiss

(both described in (Cohen, 1993)) and compared their

performance (Fig. 2), concluding that plain Gaussian

elimination performs better in this task. We found

that a large part of the time spent was in the com-

SECRET LOCKING: EXPLORING NEW APPROACHES TO BIOMETRIC KEY ENCAPSULATION

259

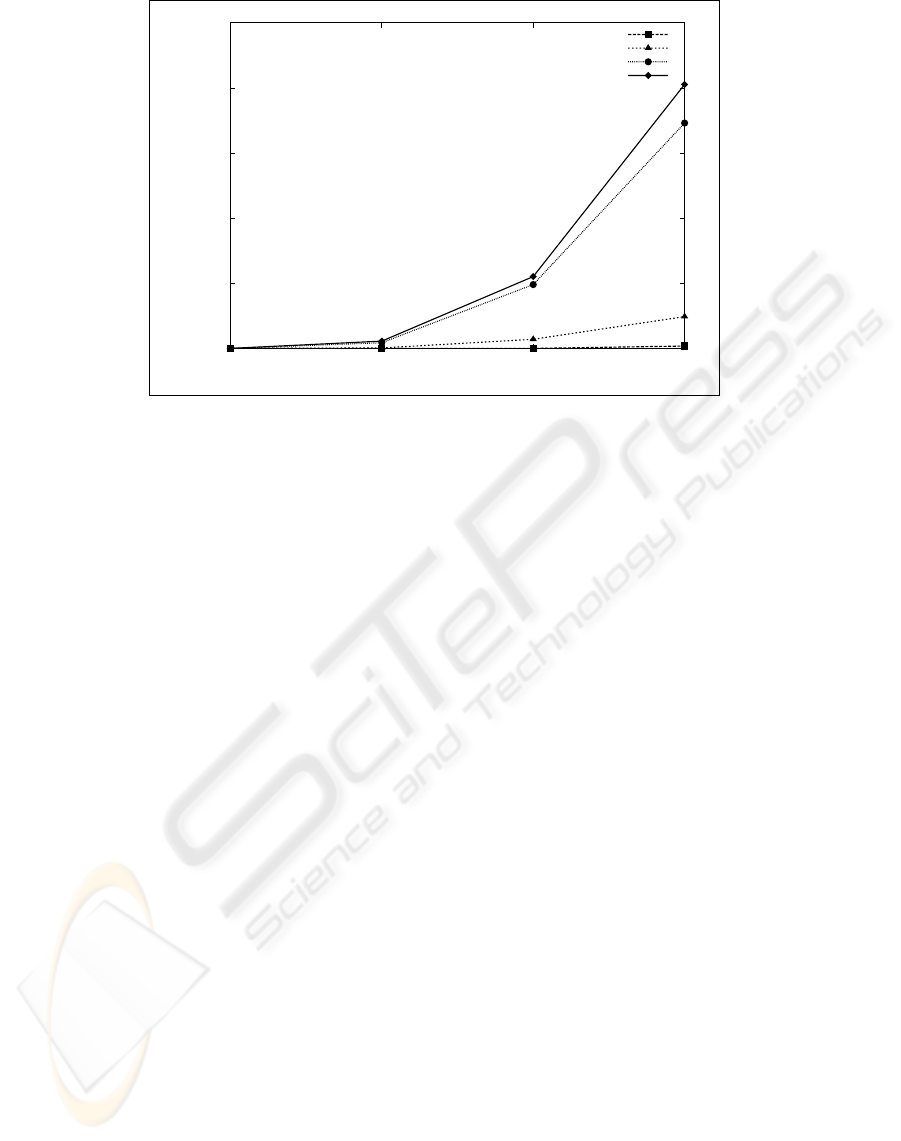
0.5

1.5

2.5

32 24 16 8

Time (s)

Feature length

e=1

e=2

e=3

e=3 (no-opt)

Figure 3: Time to generate β(φ

′

, e) and compute determinants for all its elements as a function of the feature length for

various tolerated errors. Here, 80% of φ

′

’s features are distinguishing. The no-opt line describes the time to perform the same

operations without the re-use of computation.

putation of modular inverses. Consequently, we pre-

computed all inverses in Z

∗

8191

and replaced our use

of the extended Euclidean algorithm by simple table

lookups. Since each element in Z

∗

8191

can be stored

in two bytes, the entire table can ﬁt in approximately

16 KB.

Reusing Computations. Apart from optimizing in-

dividual determinant computations we re-used in-

termediate elimination results to speed up Gaussian

elimination when several determinants are computed

in succession. Consider M

and M

, two m × m ma-

trices. During Gaussian elimination, elements in col-

umn i only affect elements in columns j > i. If the

leftmost column where M

and M

differ is i, then

the operations we perform on columns 0 through i−1

when computing det(M

) and det(M

) will be the

same, and we avoid repetition by storing the interme-

diate results. We take maximum advantage of this op-

timization by choosing an appropriate ordering when

generating all the feature sequences within the Ham-

ming ball. The results are in Fig. 3. In the case of key-

board biometrics, the number of features is approxi-

mately 15 and one noisy error must be corrected with

12 distinguishing features (numbers from (Monrose

et al., 2002)), which our implementation can compute

in a fraction of a second. A measure with twice as

much entropy, say 30 features and two noisy errors,

would also take less than half a second. These re-

sults were obtained in a relatively powerful machine

by today’s standards, however these times are sufﬁ-

ciently small that we feel conﬁdent the scheme can be

practically implemented in most current 32-bit archi-

tectures.

5 CONCLUSIONS AND FUTURE

WORK

While the security analysis in this paper does not con-

stitute a complete proof in the standard model, the

outlined heuristic connections between the security of

the scheme and well-known hard problems in compu-

tational mathematics show the difﬁculty of the under-

lying problem. The remaining open questions will be

addressed by future research. In addition, future work

includes testing of the implementation for use in the

context of other non-static biometrics (e.g., voice pat-

terns).

REFERENCES

Bleichenbacher, D. and Nguyen, P. (2000). Noisy poly-

nomial interpolation and noisy chinese remaindering.

In Advances in Cryptology—Proc. of EUROCRYPT

’2000, volume 1807 of LNCS, pages 53–69. Springer-

Verlag.

Boyen, X. (2004). Reusable cryptographic fuzzy extractors.

In Proc. of the 11

ACM Conf. on Comp. and Comm.

Secur. ACM Press.

Brickell, E. F. (1989). Some ideal secret sharing schemes.

Journal of Combinatorial Mathematics and Combina-

torial Computing, 9:105–113.

Cohen, H. (1993). A Course in Computational Algebraic

Number Theory, volume 183 of Grad. Texts in Math-

ematics. Springer-Verlag.

Davida, G. I., Frankel, Y., and Matt, B. J. (1998). On en-

abling secure applications through off-line biometric

ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS

260

identiﬁcation. In Proc. of the 1998 IEEE Symp. on

Secur. and Privacy, pages 148–157.

Doddington, G., Liggett, W., Martin, A., Przybocki, M.,

and Reynolds, D. (1998). Sheep, goats, lambs and

wolves. a statistical analysis of speaker performance

in the nist 1998 speaker recognition evaluation. In

Proc. of the 5

International Conference on Spoken

Language Processing.

Dodis, Y., Reyzin, L., and Smith, A. (2004). Fuzzy extrac-

tors and cryptography, or how to use your ﬁngerprints.

In Proc. of Adv. in Cryptology–Eurocrypt’04.

Ellison, C., Hall, C., Milbert, R., and Schneier, B. (2000).

Protecting secret keys with personal entropy. Future

Generation Computer Systems, 16:311–318.

Ghodosi, H., Pieprzyk, J., and Safavi-Naini, R. (1998). Se-

cret sharing in multilevel and compartmented groups.

In Proc. of the 3rd Australasian Conf. on Info. Se-

cur. and Privacy (ACISP’98), volume 1438 of LNCS,

pages 367–378. Springer-Verlag.

Guruswami, V. and Sudan, M. (1998). Improved decoding

of reed-solomon and algebraic-geometric codes. In

Proc. of the 39

IEEE Symp. on Found. of Comp. Sci.,

pages 28–37.

Joyce, R. and Gupta, G. (1990). Identity authorization

based on keystroke latencies. Comms. of the ACM,

33(2):168–176.

Juels, A. and Sudan, M. (2002). A fuzzy vault scheme.

In Proc. of the 2002 IEEE Internl. Symp. on Inform.

Theory, pages 480–ff.

Juels, A. and Wattenberg, M. (1999). A fuzzy commitment

scheme. In Proc. of the 6

ACM Conf. on Comp. and

Comm. Secur., pages 28–36.

Karpinski, M. and Lhotzky, B. (1991). An (ǫ, δ)-

approximation algorithm of the number of zeros of a

multi-linear polynomial over gf[q]. Technical Report

1991-8569, Uni. Bonn, Inst. f

ur Informatik, Abteilung

Monrose, F., Reiter, M. K., Li, Q., and Wetzel, S. (2001).

Cryptographic key generation from voice (extend.

abst.). In Proc. of the 2001 IEEE Symp. on Secur. and

Privacy.

Monrose, F., Reiter, M. K., and Wetzel, S. (2002). Password

hardening based on keystroke dynamics. Internl. J. of

Info. Secur., 1(2):69–83.

Shamir, A. (1979). How to share a secret. Comms. of the

ACM, 22(11):612–613.

Simmons, G. (1990). How to (really) share a secret. In

Goldwasser, S., editor, Adv. in Cryptology–Proc. of

CRYPTO’88, volume 403 of LNCS, pages p390–448.

Springer-Verlag.

Soutar, C. and Tomko, G. J. (1996). Secure private key

generation using a ﬁngerprint. In Cardtech/Securetech

Conf. Proc., volume 1, pages 245–252.

The GNU Project (1988–2005). The GNU compiler collec-

tion. http://gcc.gnu.org.

SECRET LOCKING: EXPLORING NEW APPROACHES TO BIOMETRIC KEY ENCAPSULATION

261