
ANALYTICAL STUDY OF BROADCASTING IN 802.11 AD HOC
NETWORKS
Andrey Lyakhov and Vladimir Vishnevsky
Institute for Information Transmission Problems, RAS
B. Karetny 19, Moscow, 127994, Russia
Pavel Poupyrev
ATR Adaptive Communications Research Laboratories
2-2-2 Hikaridai, Keihanna Science City, Kyoto, Japan
Keywords:
Broadcasting, IEEE 802.11, Markov models, performance study.
Abstract:
IEEE 802.11 technology becomes attractive with the implementation of various broadcast applications. For
these applications, one of the main performance indices is the mean notification time namely the interval be-
tween consecutive successful receipts of the same source’s packets. In this paper, we develop an analytical
method to study the ad hoc 802.11 network performance with broadcasting stations. The method based on a
Markov model allows the estimation of the mean notification time and the optimization of the packet genera-
tion time. The developed method has been validated by simulations and has demonstrated a high accuracy of
notification time estimation as well as the its efficiency in broadcasting optimization.
1 INTRODUCTION
IEEE 802.11 (IEEE 802.11, 1999) is one of the most
popular technologies for wireless ad hoc and mobile
networking. The fundamental access mechanism in
the IEEE 802.11 protocol is the Distributed Coordi-
nation Function (DCF), which implements the Car-
rier Sense Multiple Access with Collision Avoidance
(CSMA/CA) method.
In the majority of previous related papers, the
802.11 DCF performance was studied with unicast
transmissions: see (Bianchi, 2000; Cali et al., 2000;
Vishnevsky et al., 2002), for example. However, the
802.11 standard specifies both unicast transmissions,
and multicast or broadcast ones. Broadcasting in ad
hoc 802.11 networks is of our main interest in the pa-
per.
As an example of such broadcast applications, we
can consider the Whizbe project (Poupyrev et al.,
2002) developed in ATR, Japan. Whizbe is an appli-
cation for discovering resources such as users, prod-
uct information discounts and etc. in ad hoc networks
using broadcasting. The main goal of the application
is to provide mutual presence awareness for acquain-
tances that are in close physical proximity. Whereas
an online friend list application tells if a friend or ac-
quaintance is available for online chat, Whizbe lets
the user know if a friend or acquaintance is in physi-
cal proximity to facilitate a physical meeting or other
interaction. A number of PDAs supporting such sort
of message broadcasts and located within the same
line-of-sight area can be large and reach hundreds and
thousands (for example, in a stadium).
Another type of application, where 802.11 ad hoc
broadcasting can be successfully used, is wireless
sensor networks with distributed control. For exam-
ple,
• Wireless home temperature sensors, each of them
transmitting information to receivers of a climatic
system, fire fighting service and the home owner
work station (Cheng et al., 2002);
• Gas escape sensors in gas pipelines, where mea-
sured data are to be delivered to repair service con-
trollers. To improve reliability, several data re-
ceivers are exploited in these systems, what makes
broadcasting attractive.
In such broadcast systems, the key point is to opti-
mize the mean message generation time, that is, the
time interval separating the instances when a data
source puts its data packets into the broadcast device’s
queue. As the optimization criterion, we can con-
sider the mean notification time namely the interval
between consecutive successful receipts of the same
source’s packets. Obviously, the 802.11 DCF pecu-
liarities described below will affect the performance
index.
In the 802.11 DCF, no ARQ mechanisms are used
85
Lyakhov A., Vishnevsky V. and Poupyrev P. (2005).
ANALYTICAL STUDY OF BROADCASTING IN 802.11 AD HOC NETWORKS.
In Proceedings of the Second International Conference on e-Business and Telecommunication Networks, pages 86-91
DOI: 10.5220/0001410000860091
Copyright
c
SciTePress

with packet broadcasting. A device starts transmitting
a DATA frame containing a broadcast packet with the
following conditions:
1) The channel was free for DIFS (Distributed In-
terFrame Space) since the latest transmission in the
network;
2) The device’s backoff time has been expired;
3) There are packets to be transmitted in the de-
vice’s queue.
In particular, when a packet arrives a device ei-
ther starts the packet transmission immediately, if
the channel is free and the device is in the idle
state at the arrival time, or switches to the backoff
state otherwise. We call these immediate transmis-
sions the asynchronous ones to distinguish them from
other (synchronous) transmissions carried out after
the backoff. After passing to the backoff state, the
backoff counter is reset to the initial value b, which
is called the backoff time, measured in units of back-
off slots of duration σ, and chosen uniformly from a
set (0, . . . , W − 1). W is called the contention win-
dow and it does not depend on the number of retries
(contrary of unicast transmissions), because broadcast
transmissions are not acknowledged and hence there
are no retries at the MAC layer.
Backoff intervals are reckoned only as long as the
channel is free: the backoff counter is decreased by
one only if the channel was free for the entire previous
slot. Counting the backoff slots stops when the chan-
nel becomes busy, and backoff time counters of all
stations decrement only when the channel is sensed
idle for DIFS. When the backoff counter attains its
zero value, the station starts transmission. A collision
happens when backoff counters of two or more sta-
tions are zeroed simultaneously. All packets of sta-
tions involved in the collision are lost.
A device that has completed a packet transmission
returns to the backoff state. If the device’s queue ap-
pears to be empty at the end of the backoff time, the
device becomes idle.
Further, in Sections 2 and 3 we develop an analyt-
ical model, which considers all significant DCF fea-
tures and provides the mean notification time estima-
tion. In Section 4, we give some numerical research
results obtained by both our analytical method and
simulations, which allows us to validate the devel-
oped method. The obtained results are summarized
in Section 5.
2 ANALYTICAL MODEL
Let us consider an ad hoc 802.11 network of N sta-
tistically homogeneous stations generating broadcast
packets of the same fixed length with an identical rate
λ ≪ (Nσ)
−1
. Generation intervals are assumed to be
distributed exponentially. Every station’s queue can
contain no more than B packets. The channel is ideal,
that is, there are no noise-induced distortions. Signal
propagation time is assumed to be negligible.
The analytical model to be developed is intended
for the determination of the optimal generation rate
λ
opt
, when the mean notification time T
not
is mini-
mal.
As in (Bianchi, 2000) and (Vishnevsky et al.,
2002), let us subdivide the time of the network op-
eration into non-uniform virtual slots such that:
• Every station with non-empty queue changes its
backoff counter at the start of a virtual slot and
begins a synchronous transmission if the counter
value becomes zero.
• If a transmission happens within a given virtual
slot, the slot is ended by the DIFS closing the trans-
mission.
• If nobody transmits during σ since the current slot
beginning, this slot duration is equal to σ.
Such a virtual slot is either (a) an “empty” slot
σ in which no station transmits, or (b) a “synchro-
nous” slot when one or more stations transmit syn-
chronously or (c) an “asynchronous” slot when a sta-
tion transmits asynchronously. Note that an asynchro-
nous transmission can be considered as always suc-
cessful since, firstly, it can be performed only in a slot
when no other stations transmit synchronously (oth-
erwise it will sense the channel busy at the slot begin-
ning and defer from its transmission), and secondly,
we can neglect the probability that two or more pack-
ets arrive to queues for σ because λ ≪ (N σ)
−1
.
Following (Bianchi, 2000), we describe a station
state by the couple (i, k), where i = 0, 1 is an indi-
cator of non-empty queue and k = 0, . .., W -1 is a
backoff counter value, and a station behavior by the
Markov chain shown in Fig.1. In the chain, all transi-
tions happen at virtual slot borders.
Figure 1: Markov chain.
State (0,0) corresponds to the idle state of the con-
sidered station. In states (0, 1)...(0,W-1), the station
is in the backoff state, but its queue is empty. At last,
(1, 0),... , (1,W -1) are the states when the station’s
queue is not empty.
ICETE 2005 - WIRELESS COMMUNICATION SYSTEMS AND NETWORKS
86

Let us introduce the following notation:
P {i
2
, k
2
|i
1
, k
1
} is the probability of one-step tran-
sition from (i
1
, k
1
) to (i
2
, k
2
).
P
0
is the probability that a queue becomes empty
after completing its synchronous transmission.
P
S
is the probability that at least one packet arrives
in the considered station’s queue for a virtual slot un-
der the condition that the queue was empty at the slot
beginning. Obviously, the probability consists of two
items: P
S
= P
F
S
+ P
E
S
, where P
F
S
and P
E
S
are the
arrival probabilities for non-empty and empty slots,
respectively, under the same condition as above.
P
T
is the probability that at least one packet arrives
in the considered station’s queue for a packet trans-
mission time, including the closing DIFS.
To find stationary probabilities α (i, k) of the states
in Fig. 1, let us define non-null transition probabili-
ties:
P {1, k|1, k + 1} = 1, k ∈ [0, W − 2] : backoff
counter decrement, the queue is not empty.
P {1, k|1, 0} =
1−
P
0
W
, k ∈ [0, W − 1] : syn-
chronous transmission of the station, after which
its queue remains to be non-empty. Here,
P
0
=
P
0
e
−λDIFS
is the probability that a queue becomes
empty after completing its synchronous transmission
and keeps to be empty after DIFS closing the trans-
mission.
P {0, k|1, 0} =
P
0
W
, k ∈ [0, W − 1] : synchro-
nous transmission of the station, after which its queue
becomes empty.
P {1, k|0, k + 1} = P
S
, k ∈ [0, W − 2] : back-
off counter decrement, and a packet arrives in the sta-
tion’s empty queue.
P {0, k|0, k + 1} = 1 − P
S
, k ∈ [0, W − 2] :
backoff counter decrement, the queue remains to be
empty.
P {1, k|0, 0} =
P
F
S
+P
E
S
P
T
W
, k ∈ [0, W − 1] :
the station switches from the idle state to the backoff
state. The switch takes place, if either a packet arrives
when the channel was busy, or one more packet ar-
rives during the station’s asynchronous transmission.
P {0, k|0, 0} =
P
E
S
(1−P
T
)
W
, k ∈ [1, W − 1] : the
transition corresponds to the station’s asynchronous
transmission, after which the station’s queue is empty
and the backoff counter b = k > 0.
P {0, 0|0, 0} = 1 − P
S
+
P
E
S
(1−P
T
)
W
: there are no
packet arrivals in the queue, or the station’s asynchro-
nous transmission takes place, after which the sta-
tion’s queue is empty and the backoff counter b = 0.
Now we can determine stationary probabilities
α(i, k). Using global balance equations and the nor-
malizing condition
P
(i,k)
α(i, k) = 1, we obtain:
α (0, 0) =
1 − P
S
+
W + 1
2
× (1)
×
P
S
+
W P
2
S
1−(1−P
S
)
W
− P
E
S
(1 − P
T
)
P
0
−1
,
α(1, 0) =
W P
2
S
1−(1−P
S
)
W
− P
E
S
(1 − P
T
)
P
0
· α(0, 0),
(2)
α(0, j) = P
S
·
1 − (1 − P
S
)
W −j
1 − (1 − P
S
)
W
· α(0, 0), (3)
j = 1, . . . , W − 1,
α (1, j) =
W − j
W
[P
S
· α (0, 0) + α (1, 0)]−α (0, j) ,
(4)
j = 1, . . . , W − 1,
Let τ be the probability of the station’s synchro-
nous transmission for a virtual slot. Similarly to
(Bianchi, 2000; Cali et al., 2000), we assume that
the probability depends neither on the previous his-
tory, nor on the behavior of other stations. Obviously,
τ = α(1, 0). Moreover, the probability of synchro-
nous transmission failure due to a collision is P
C
=
1 − (1 − τ )
N−1
, and the probability of the station’s
asynchronous transmission for a virtual slot is τ
a
=
α(0, 0)P
E
S
, where P
E
S
= (1−τ )
N−1
[1−exp{−λσ}]
since we have neglected the case, when two or more
packets arrive for σ.
Let us find durations of non-empty slots:
• “Synchronous” slot: t
S
= t
P
+DIFS, where t
P
is a
DATA frame transmission time;
• “Asynchronous” slot: the mean duration is t
A
=
σ
2
+ t
P
+DIFS.
The probability P
T
that at least one packet arrives
in the station’s queue for t
S
is P
T
= 1 − exp(−λt
S
).
To find the probability P
F
S
, we need to know prob-
abilities of all possible kinds of slots under the con-
dition that the considered station does not transmit
in the slot. Under the condition, the “empty” slot
probability is Q
E
= (1 − τ − τ
a
)
N−1
, the “syn-
chronous” slot probability is Q
S
= 1 − (1 − τ)
N−1
,
and the “asynchronous” slot probability is Q
A
=
1 − Q
E
− Q
S
. So we have
P
F
S
= (Q
S
+ Q
A
) P
T
.
To complete the model definition, it remains to find
probability P
0
that a queue becomes empty after fin-
ishing the current packet service. A packet service
starts at the instance of either the packet arrival in an
empty queue or completing the transmission of the
previous packet in the queue. If a packet arrives in
an empty queue and is transmitted asynchronously,
ANALYTICAL STYDY OF BROADCASTING IN 802.11 AD HOC NETWORKS
87
we deal with the asynchronous service case, when a
packet is served for the fixed time t
P
. With synchro-
nous service, the service time is random.
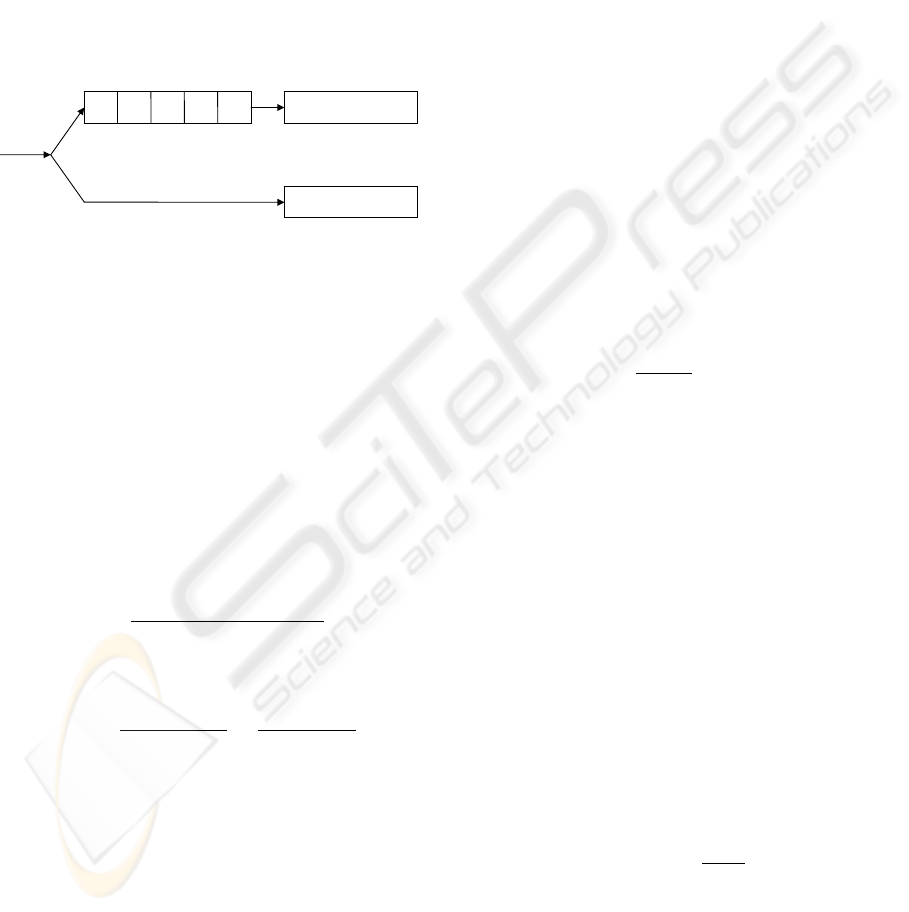
Let us describe a device’s queue change process by
the auxiliary model shown in Fig. 2. With the model,
we assume that a packet arriving at a device not en-
gaged in servicing other packets is serviced asynchro-
nously (and hence successfully) with probability p
a
.
Otherwise, the packet is put into a queue of size B.
After standing in the queue, it is serviced synchro-
nously for a random time distributed exponentially
with the average value T
S
.
Ȝ
Synchronous
transmission
Asynchronous
transmission
ʌ
0
p
a
t
P
T
S
Queue
1
B
Figure 2: Queue change process.
Under these assumptions, we can use a birth-and-
death process to describe how the length i of the syn-
chronously serviced packets queue changes. Since the
birth rate is λ
0
= (1 − p
a
) λ with i = 0 and λ with
0 < i < B, while the the death rate is 1/T
S
, we ob-
tain the following formula for the steady-state proba-
bilities:
π
i
= π
0
λ
0
λ
i−1
T
i
S
, i = 1, . . . , B. (5)
Obviously, π
B
is the probability of packet rejection
because of buffer overflow. Therefore, the probability
that a queue becomes empty after completing its syn-
chronous transmission is equal to P
0
= π
1
/(1 − π
0
).
Moreover, since
π
0
=
1
1 + (1 − p
a
)
B
P
i=1
(λT
S
)
i
, (6)
we obtain
P
0
=
1
B
P
i=1
(λT
S
)
i−1
=
1 − λT
S
1 − (λT
S
)
B
. (7)
In the next section, we will estimate the probability
p
a
and the average time T
S
of synchronous service,
as well as the main performance index T
not
.
3 ESTIMATION OF
PERFORMANCE INDICES
Let us subdivide all packets, which arrive at some sta-
tion A during all possible virtual slots identified by
couple (i, k) and are serviced synchronously, into the
following 4 categories:
1. Packets arriving for slots (1, k);
2. Packets arriving for slots (0, k > 0);
3. Packets arriving for slot (0,0), when a device dif-
ferent from A transmits;
4. Packets arriving during an asynchronous transmis-
sion of device A.
For each of the categories, we will count the aver-
age number n
i
of these packets arriving for a virtual
slot and the average number n
0
i
of these packets ar-
riving for a virtual slot in empty queue. It is easy to
show that
T
S
=
"
(T
∗
S
+ DIFS)
4
X
i=1
n
i
− n
0
i
+
4
X
i=1
T
i
S
n
0
i
#
/
/
4
X
i=1
n
i
, (8)
p
a
= τ
a
/
τ
a
+
4
X
i=1
n
0
i
!
, (9)
where
T
∗
S
=
W − 1
2
t
V S
+ t
P
and t
V S
= Q
E
σ +Q
S
t
S
+Q
A
t
A
is the average dura-
tion of a virtual slot, when the given device A does not
transmit. Moreover, T
i
S
is the average service time for
category i packets arriving in empty queue.
To estimate T
S
and p
a
, using (8) and (9), it re-
mains to find n
i
, n
0
i
and T
i
S
for each of introduced
categories. Let us do it.
Category 1. In the case, packets can arrive in
empty queue of the considered station A only for the
DIFS closing the station’s transmission and only, if
the transmitted packet was the last in the queue. So
we have
n
0
1
=
1 − e
−λ·DIFS
P
0
· α(1, 0),
n
1
= λt
V S
W −1
X
k=1
α(1, k) + λt
S
· α(1, 0),
and
T
1
S
= T
∗
S
+
DIFS
2
.
Category 2. Since only the first of packets arriving
in the queue for each of the slots can find the queue
empty, we have
n
0
2
= Q
∗
W −1
X
k=1
α(0, k),
ICETE 2005 - WIRELESS COMMUNICATION SYSTEMS AND NETWORKS
88

n
2
= λt
V S
W −1
X
k=1
α(0, k),
and
T
2
S
= t
P
+
t
V S
Q
∗
n
0
2
W −1
X
k=1
k −
1
2
α(0, k),
where
Q
∗
= Q
E
1 − e
−λσ
+ Q
S
1 − e
−λt
S
+Q
A
1 − e
−λt
A
.
Category 3. For this case, we have
n
0
3
=
Q
S
1 − e
−λt
S
+ Q
A
1 − e
−λt
A
α(0, 0),
n
3
= λ (Q
S
t
S
+ Q
A
t
A
) α (0, 0) ,
T
3
S
= T
∗
S
+
Q
S
t
S
+ Q
A
t
A
2 (1 − Q
E
)
.
Category 4. As for Category 2, in this case we
should distinguish the first of these arriving packets
and others. So
n
0
4
= P
E
S
1 − e
−λt
S
α(0, 0) = P
T
τ
a
,
n
4
= τ
a
λt
S
, T
4
S
= T
∗
S
+
t
S
2
.
Finally, taking into account of asynchronous trans-
missions, we obtain the mean notification time:
T
not
=
1
λ [π
0
p
a
+ (1 − π
0
p
a
) (1 − P
C
) (1 − π
B
)]
.
(10)
We adopt the following iterative procedure to cal-
culate this performance index.
Step 0. Define an initial value for P
0
.
Step 1. Define initial values for transmission prob-
abilities τ and τ
a
.
Step 2. Calculate, firstly, probabilities P
F
S
and P
E
S
and then the steady-state probabilities α(i, k). Us-
ing α(0, 0) and α(1, 0), calculate modified values for
transmission probabilities. If differences of initial and
modified values are greater than a predefined limit ∆
t
,
repeat this Step, using new initial values for τ and τ
a
– the half-sums of their old initial values and the mod-
ified values.
Step 3. Calculate, firstly, T
S
and p
a
, using (8) and
(9), secondly, the steady-state probabilities π
i
and
then the modified value of probability P
0
. If the dif-
ference of initial and modified values of P
0
is greater
than a predefined limit ∆
P
, return to Step 1.
Step 4. Calculate the mean notification time by
(10).
We do not prove exactly the convergence of this it-
erative technique due to its complexity. In practice,
numerous examples of adopting the technique with
various values of network and traffic parameters have
shown that this technique provides very fast conver-
gence to the solution and high speed of T
not
calcula-
tion.
4 NUMERICAL RESULTS
To validate our model, we have compared its results
with that obtained by GPSS (General Purpose Sim-
ulation System) simulations (Schriber, 1974; GPSS
World, 1998). The object of our numerical investiga-
tions was an ad hoc 802.11b (with Short Preamble)
network (IEEE 802.11b, 1999) of N statistically ho-
mogeneous stations generating broadcast packets of
the same length L. The every station’s buffer size B
was chosen equal to 100 packets. In our simulation
model, we took into account of all real features of the
802.11 MAC protocol and did not adopt the assump-
tions used in analytical modelling and described in
Section 2. In each run (it took about an hour on the
average) of the simulation model, we observed values
of the measured performance indices and stopped the
simulation when their fluctuations became quite small
(within 0.5%).
In Fig. 3 we show how the mean notification time
depends on the average generation time T
g en
=
λ
−1
with the packet length L = 1000 bytes that
corresponds to the DATA transmission time t
P
=
850 µs. The dependency has been obtained analyti-
cally (the “Math” curve) and validated by simulation
(the “GPSS” circles). In particular, the comparison
has shown a high accuracy of the analytical model:
the errors never exceed 5% with the mean notification
time estimation.
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Math
y=x
GPSS
Figure 3: Mean notification time T
not
(s) versus the average
generation time T
gen
(s) with L = 1000 bytes and N = 50:
Math – analytical method; GPSS – simulation.
The curve T
not
(T
g en
) in Fig. 3 has a clear mini-
mum at T
g en
= T
opt
g en
≈ 0.48 s. When T
g en
exceeds
T
opt
g en
, most of packets are transmitted asynchronously
(and hence, successfully) and the mean notification
time is approximately equal to T
g en
. However, in this
case there are wide gaps between packet arrivals, and
the network capacity is used ineffectively. With high
ANALYTICAL STYDY OF BROADCASTING IN 802.11 AD HOC NETWORKS
89

generation rates (T
g en
< T
opt
g en
), most of packets are
transmitted synchronously, what causes frequent col-
lisions and hence T
not
growth. Moreover, there is a
threshold (≈ 0.015 s in Fig. 3) of T
g en
, below which
the network becomes saturated and buffers are almost
always overflowed. In this saturation area, T
not
does
not change.
Fig. 4 shows dependencies T
not
(T
g en
) for various
packet lengths. It proves that the optimal generation
rate depends essentially on the packet length (as well
as on the number N of stations – these results are not
shown). Concerning the form of this dependency, it
appears that the optimal average generation time de-
pends on both the packet length and the number N of
stations almost linearly.
0 0.1 0.2 0.3 0.4
0
0.1
0.2
0.3
0.4
0.5
L=500 byte
L=1000 byte
L=2000 byte
y=x
a
b
c
Figure 4: Mean notification time T
not
(s) versus the average
generation time T
gen
(s) with N = 50 and various packet
lengths L: (a) L = 500 bytes; (b) L = 1000 bytes; (c)
L = 2000 bytes.
5 CONCLUSION
In this paper, we have developed a novel analytical
method to study the performance of an ad hoc 802.11
network of stations generating broadcast packets. The
method based on Markov models allows estimating
the main performance index of such a network: the
mean notification time namely is the interval between
consecutive successful receipts of the same source’s
packets. Using the method, we succeeded in optimiz-
ing the packet generation time to minimize the mean
notification time.
According to numerical results obtained by both
the developed method and simulations, our method
is quite exact: the errors never exceed 5% with the
notification time estimation. This method provides a
high speed of calculating the values of performance
indices, which has allowed us to perform the exhaus-
tive search of optimal packet generation time.
As a future research activity in this direction, we
propose extensions of this method to take into account
the cases when (a) the wireless channel is not ideal;
and (b) broadcasting stations can be hidden from each
other.
ACKNOWLEDGMENT
This work was partially supported by Russian Science
Support Foundation.
REFERENCES
ANSI/IEEE Std 802.11 (1999). Wireless LAN Medium Ac-
cess Control (MAC) and Physical Layer (PHY) Speci-
fications. IEEE Press, New York, 1999 edition.
Bianchi, G. (2000). Performance Analysis of the
IEEE 802.11 Distributed Coordination Function. In
IEEE Journal on Selected Areas in Communications
18(3):535-547.
Cal
´
ı, F., Conti, M., Gregory E. (2000). Dynamic Tuning
of the IEEE 802.11 Protocol to Achieve a Theoreti-
cal Throughput Limit. In IEEE/ACM Transactions on
Networking 8(6):785-799.
Vishnevsky V.M., Lyakhov A.I. (2002). IEEE 802.11
Wireless LAN: Saturation Throughput Analysis with
Seizing Effect Consideration. In Cluster Computing
5(2):133-144.
Poupyrev P., Kosuga M., Davis P. (2002). Analysis of Wire-
less Message Broadcast in Large Ad Hoc Networks of
PDAs. In Proceedings of Forth IEEE conference on
Mobile and Wireless Communications Networks, pp.
299-303.
Cheng L., Marsic I. (2002). Piecewise Network Aware-
ness Service for Wireless/Mobile Pervasive Comput-
ing. In Mobile Networks and Applications (MONET)
7(4):299-303.
Schriber, T.J. (1974). Simulation using GPSS. John Wiley
& Sons.
GPSS World (1998). www.minutemansoftware.com.
IEEE 802.11b: Supplement to ANSI/IEEE Std 802.11
(1999). (IEEE 802.11, 1999). Higher-Speed Physical
Layer Extension in the 2.4 GHz Band. IEEE Press,
New York.
ICETE 2005 - WIRELESS COMMUNICATION SYSTEMS AND NETWORKS
90
