A NOVEL REAL-TIME SELF-SIMILAR TRAFFIC

DETECTOR/FILTER TO IMPROVE THE RELIABILI

TY OF A

TCP BASED END-TO-END CLIENT/SERVER IN

TERACTION

PATH FOR SHORTER ROUNDTRIP TIME

Wilfred W. K. Lin, Allan K. Y. Wong, Richard S.L. Wu

Department of Computing, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong S.A.R.

Tharam S. Dillon

Faculty of Infornation Technology, University of Technology Sydney,Broadway, Sydney, Australia

Keywords: real-time traffic pattern detection (RTPD), stationary, asymptotically second-order self-similarity, CAB,

Gaussian property, fractal

Abstract: The self-similarity (

S ) filter is proposed for real-time applications. It can be used independently or as an

extra component for the enhanced RTPD (real-time traffic pattern detector) or E-RTPD. The

filter

basis is the “asymptotically second-order self-similarity” concept (alternatively called

statistical

OSS

2 or OSSS

2 ) for stationary time series. The focus is the IAT (inter-arrival times)

traffic. The filter is original because similar approaches are not found in the literature for detecting self-

similar traffic patterns on the fly. Different experiments confirm that with help form the

filter the FLC

(Fuzzy Logic Controller) dynamic buffer size tuner control more accurately. As a result the FLC improves

the reliability of the client/server interaction path leading to shorter roundtrip time (RTT).

1 INTRODUCTION

It is hard to harness the roundtrip time (RTT) of an

end-to-end client/server interaction path over a TCP

channel in time-critical applications. The problem is

the heterogeneity and sheer size of the Internet. If

the path error probability for retransmissions is

the average number of trials (ANT) for successful

transmission is

)1(

lim)]1([

ρρ

−

≈−

∞→

∞

−

∑

The value

encapsulates different faults and

errors, and one of them is caused by buffer overflow

along the end-to-end interaction path. There are two

levels of buffer overflows: a) system/router level

that includes all activities inside the TCP channel,

and b) user level that involves the buffer at the

receiving end. Methods to prevent network

congestion that causes router buffer overflow

include active queue management (AQM) (Braden,

1998). One effective approach to eliminate user-

level buffer overflow to improve the end-to-end path

reliability is dynamic buffer size tuning (Wong,

2002). The accuracy and stability of the tuning

process, however, are affected by the Internet traffic

patterns in terms of messages' inter-arrival times

(IAT). To resolve this problem the previous real-

time traffic pattern detector (RTPD) (Lin, 2004) was

proposed. With the detected results the dynamic

buffer size tuners can mitigate/nullify the ill effects

by traffic on system stability and performance in a

dynamic fashion. The RTPD, however, does not

detect self-similar traffic, and this leads to the

proposal of the self-similarity (

) filter in this

paper. Inclusion of the

filter into RTPD created

the enhanced RTPD (E-RTPD). It will be

demonstrated later how E-RTPD helps the Fuzzy

Logic Controller (Lin, 2004B) self-tune better on the

fly to gain more accurate and smoother user-level

dynamic buffer size tuning and shorter RTT as a

result.

The Internet involves many different client/server

interaction protocols (Lewandowski, 1998), and its

W. K. Lin W., K. Y. Wong A., S.L. Wu R. and S. Dillon T. (2005).

A NOVEL REAL-TIME SELF-SIMILAR TRAFFIC DETECTOR/FILTER TO IMPROVE THE RELIABILITY OF A TCP BASED END-TO-END

CLIENT/SERVER INTERACTION PATH FOR SHORTER ROUNDTRIP TIME.

In Proceedings of the Second International Conference on e-Business and Telecommunication Networks, pages 94-101

DOI: 10.5220/0001413000940101

 SciTePress

traffic follows the power law (Medina, 2000). Over

time the traffic in any part of the Internet may

change suddenly, for example, from LRD (long-

range dependence) to SRD (short-range

dependence) or vice versa (Willinger, 2003). Using

the Hurst (H) effect (i.e.

H (Taqqu, 2003)) as the

yardstick then

15.0

< H

is for LRD and

5.00 ≤< H

for SRD. If }1:{ ≥= lXX

a time series aggregate of size

in a stochastic

process X, its autocorrelation function (ACF)

(correleogram) is

∑

−

rlr

)(

, where

is the

autocorrelation of

and l for the aggregate level.

The ACF of LRD traffic is non-summable (i.e.

∞≈

∑

∞→

−

), but it is summable for SRD (i.e.

∞<

∑

∞→

−

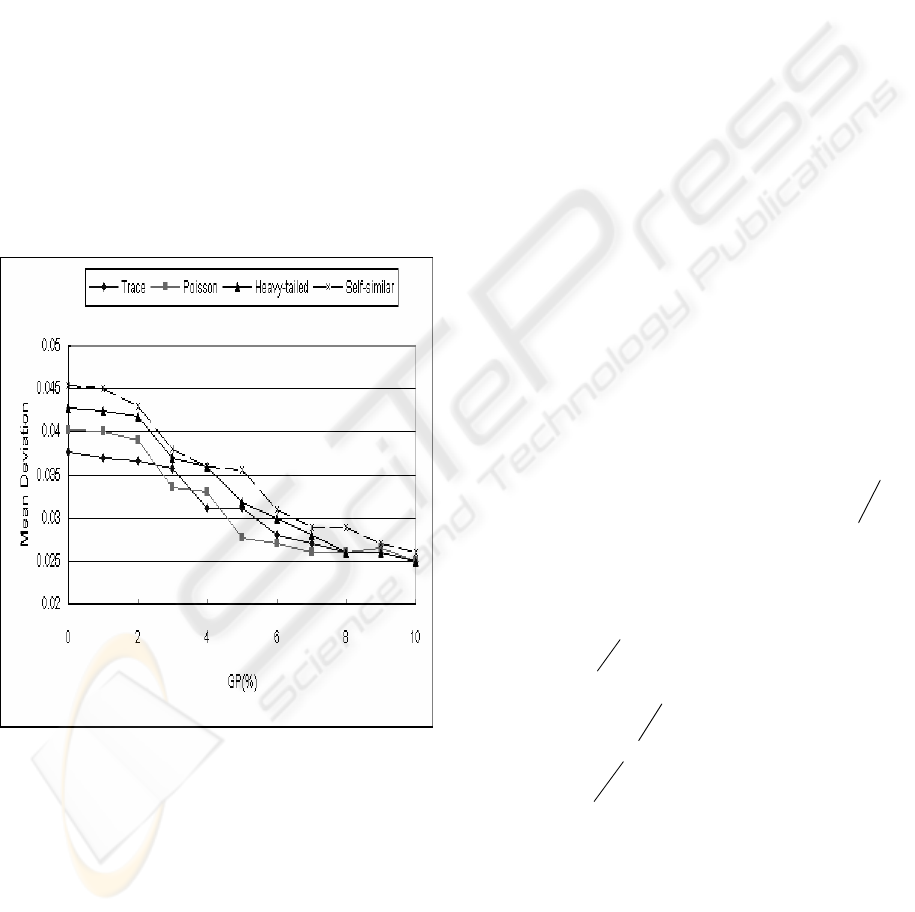
Figure 1: Internet traffic impact on FLC accuracy

It is impractical to monitor the overwhelming

number of network parameters in the Internet to

harness the client/server RTT. A practical approach

is to treat the Internet as a “black box” and measure

the end-to-end RTT to interpret the channel

behavior. This is the IEPM (Internet End-to-End

Performance Measurement (Cottrel, 1999))

approach. Any sudden changes in the IAT traffic

pattern affect the performance of applications

running on the Internet. The traffic’s ill effect on the

FLC stability and accuracy (Lin, 2004) is an

example. Figure 1 shows how the mean deviations

(MD) from the FLC steady-state reference due to

traffic changes in one deployment. Traffic self-

similarity (or self-affinity) consistently produces the

largest deviations compared to heavy-tailed and

Markovian traffic. Two objects are geometrically

similar if one is derived from another by linear

scaling, rotation or translation. The GP% (gradient

percentage) in Figure 1 is a derivative (D) control

parameter in FLC. For the same GP value different

traffic patterns produce different MD values. The

reconfigurable version of the FLC uses the RTPD to

detect a traffic pattern on the fly and utilizes the

result to neutralize traffic ill effects by choosing the

correct GP value accordingly (Lin, 2004). The

RTPD differentiates LRD from SRD and identifies

heavy-tailed traffic, but it does not detect self-

similar patterns. Combining the previous RTPD

model with the self-similarity (

S ) filter (or simply

S filter) creates the enhanced RTPD (E-RTPD),

which has the capability to identify self-similarity

and compute its dimension (D). If an object is

geometrically, recursively split into similar pieces,

then at the

iteration step the total measure of the

object is “product of the number of similar pieces

and

O ”. The parameter O is the splitting

resolution or reduction. The Cantor Set is an

example in which a line segment of interval [0,1] is

drawn as the first step (i.e.

0=K

). This line is then

manipulated by the subsequent steps: a) divide the

line into three equal portions (i.e. resolution is

)

and remove the middle portion (i.e.

), b)

remove the middle portions from the remaining two

(i.e.

), and c) repeat the last step ad infinitum.

The

iteration produces

similar line segments

of length

s )

each. The Cantor Set’s self-

similarity dimension is defined by the

formula

)

(

or alternatively

63.0]

))3log((

))2log((

[ ≈=

An object is fractal if its D value is non-integer.

Different non-converging dimension definitions

exist, the Cantor Set provides only a conceptual

basis. A stochastic process

)(tX is

H , self-

similar and fractal, provided that its two finite-

dimensional distributions ,

)(atX and )(tXa

are identical for

0>a

. That is, the following

expression holds:

A NOVEL REAL-TIME SELF-SIMILAR TRAFFIC DETECTOR/FILTER TO IMPROVE THE RELIABILITY OF A

TCP BASED END-TO-END CLIENT/SERVER INTERACTION PATH FOR SHORTER ROUNDTRIP TIME

≡)}()...(),({

21 n

atXatXatX

)}(),...({

1 n

atXatXa

;

≡ means equality and H is the scaling exponent.

2 RELATED WORK

The previous RTPD is enhanced from the traditional

R/S (rescaled adjusted statistics) approach for non-

real-time (i.e. “post-mortem”) applications. The

enhanced R/S (i.e. E-R/S) is a real-time

“

filtrationSRRTM ++ /

” package.

The

element is a micro Convergence

Algorithm (CA) or MCA implementation (Wong,

2001). The CA is the technique adopted from the

IEPM (Internet End-to-End Performance

Measurement) problem domain (Cottrel, 1999). The

MCA, which predicts the mean of a traffic

waveform quickly and accurately, operates as a

logical object to be invoked for service anytime and

anywhere by message passing. It helps the R/S

mechanism differentiates SRD from LRD on-line.

The filtration process activates an appropriate filter

to identify the exact traffic pattern; for example, the

modified QQ-plot filter identifies heavy-tailed

distributions. The main RTPD contribution is that it

can be a part of any time-critical application, which

uses it to detect traffic patterns on the fly. These

applications can then use the detected result to self-

tune for better system performance (Lin, 2004).

Similar to its R/S predecessor, the E-R/S calculates

the Hurst (H) parameter/value but on-line. The

15.0 << H

range means LRD traffic (e.g. heavy-

tailed and self-similar traces) and

5.00 ≤< H

for

SRD (short-range dependence, e.g. Markovian

traffic) (Molnar, 1999).

The traditional R/S is defined by

)var(

},...,2,1:min{},....,2,1:max{

kiWkiW

−

The parameter

W is computed as

∑

−=

XXW

)(

for i=1,2,…k, where

is the mean of.

∑

The best value for k is usually found by trial and

error, and this becomes the drawback because R/S

accuracy and speed depend on k. The R/S ratio is the

rescaled range of the stochastic process X over a

time interval k,

},...2,1:{ kiX

= . A useful R/S

feature is the log-log of

)

(≈

, which

yields the H value.

The CA operation, which is derived from the

Central Limit Theorem, is summarized by the

equations: (2.1) and (2.2). The estimated mean

M in the

i prediction cycle is based on the fixed

F (flush limit) number of data samples. The cycle

time therefore depends on the interval for collecting

the F samples. It was confirmed previously that

M has the fastest convergence for F=14 (Wong,

2001). Other parameters include: a)

1−i

is the

feedback of the last predicted mean to the current

M prediction cycle, b)

is the j

data item

sampled in the current i

cycle,

)1(,....,3,2,1

−

, and c)

is the first

data sample when the MCA had started running. In

the E-R/S,

M replaces

to yield .

∑

−=

imi

MXW

)(

This replacement makes the E-R/S more suitable for

real-time applications because the number of data

items (e.g. IAT) to calculate

W becomes

predictable (i.e.

). In real-life applications

∑

will need much longer computation

time than

M for two reasons: a)

is usually larger

than

, and b) the IAT among

X could be so

large that the product of “

and average IAT”

means a significant time delay. In an E-RTPD

implementation the E-/RS,

and filter

modules are running in parallel. The E-RTPD

execution time depends on the E-R/S module, which

has the longest execution. The Intel’s VTune

Performance Analyzer (Intel VTune, 2002) records

from the Java RTPD prototype the following

average execution times in clock cycles: 981 for E-

R/S, 250 for

, and 520 for the modified QQ-

plot filter. The novel

filter provides RTPD with

the additional capability to quickly detect self-

similar traffic on the fly.

1);2.2.(..........

);1.2(..........

≥=

−=

−

∑

imM

ICETE 2005 - GLOBAL COMMUNICATION INFORMATION SYSTEMS AND SERVICES

3 THE SELF-SIMILARITY

FILTER

LRD traffic has at two basic components: heavy-

tailed and self-similar. The proposed self-similarity

(

S ) filter differentiates heavy-tailed IAT patterns

from self-similar ones. Self-similarity in many

fractal point processes results from heavy-tailed

distributions, for example, FRP (Fractal Renewal

Process) inter-arrival times. The heavy-tailed

property, however, is not a necessary condition for

self-similarity because at least the FSNDPP

(Fractal-Shot-Noise-Driven Poisson Process) does

not have heavy-tailed property. The

S filter basis

is the “asymptotically second-order self-similarity”

concept, or simply called statistical

OSS

OSSS

2 , which associates with a sufficiently

large aggregate level or lag

in a stochastic process

X. For an aggregate

}1:{ ≥= lXX

size

in X, OSSS

2 for ∞→

means that

the associated autocorrelation function (ACF),

namely

)(lr

(for

) is proportional to

)22( H

−−

. OSSS

2 is LRD for its ACF is non-

summable, as indicated by .

=)(lr

∞=

∑

∞

−1l

The condition of “

)22(

)(

llr

−−

∝ for

∞

→

”

is mathematically equivalent to the slowly decaying

variance property. That is, the variance of the mean

of sample size

decays more slowly than

. This

phenomenon is represented by the expression:

−

∝ mXVar

)( . For a stationary OSS

process X and

15.0 <

the value of

H22 −=

should apply. Equations (3.1) and

(3.2) summarize the

OSSS

2 property and they

hold for the weaker condition in equation (3.3). The

slowly decaying variance property is clear if a log-

log plot is produced for equation (3.1). As shown by

equation (3.4),

))(log( XVar is a constant,

))(log(

XVar versus )log(m yields a straight

line with slope

− . The H value can then be

calculated by the

)

−=H

formula. The

S filter finds

for

on the fly.

The

)(

XVar calculation uses the mean value

)(

XE estimated by the

process.

)(

XE is

∑

+−=

−

mln

1)1(

conceptually, and the

key for the

S filter operation is to choose a

sufficiently large

, which is the multiples (i.e. C)

to virtually satisfy ∞→

;

FCm *

for estimating

. The detected result

is available at the

Ag time point. In Figure 2 for

example, the

result for aggregate 2 is available at

the point of

Ag .

)1.3).....((

)(

)22(

XVar

−

)2.3)....(()( krlr

∞→m

lim

)3.3)....(()( krlr

)4.3)....(log())(log())(log( mXVarXVar

−=

The process in the

S filter to calculate

is the

“continuous aggregate based (CAB)” method. The

CAB evaluates if an aggregate is stationary by

checking its Gaussian property or “Gaussianity”

(Arvotham, 2001) by the kurtosis and skewness

metrics. A symmetrical normal distribution has

perfect Gaussianity indicated by

kurtosis

and

skewness

. Statistically measured kurtosis

and skewness values are rarely perfect, and

reasonable limits can be used to indicate the

presence of a bell curve, which belongs to the

exponential family of independent stationary

increments. The

S filter follows the CAB

procedure and finds

by linear regression, and the

quality of which can be judged by the coefficient of

determination or

between 0 and 1 (Jain, 1992).

Higher

implies better quality for the linear

regression. By the predefined threshold

Th (e.g.

0.85 or 85%) the

S filter can reject a hypothesis of

self-similarity in

for

ThR < . The CAB

operation in Figure 2 works with the aggregates

lAg

in a stochastic process X along the time axis.

Assuming: a) P1, P2, and P3 are the log-log plots for

three successive aggregates based on equation (3.4),

A NOVEL REAL-TIME SELF-SIMILAR TRAFFIC DETECTOR/FILTER TO IMPROVE THE RELIABILITY OF A

TCP BASED END-TO-END CLIENT/SERVER INTERACTION PATH FOR SHORTER ROUNDTRIP TIME

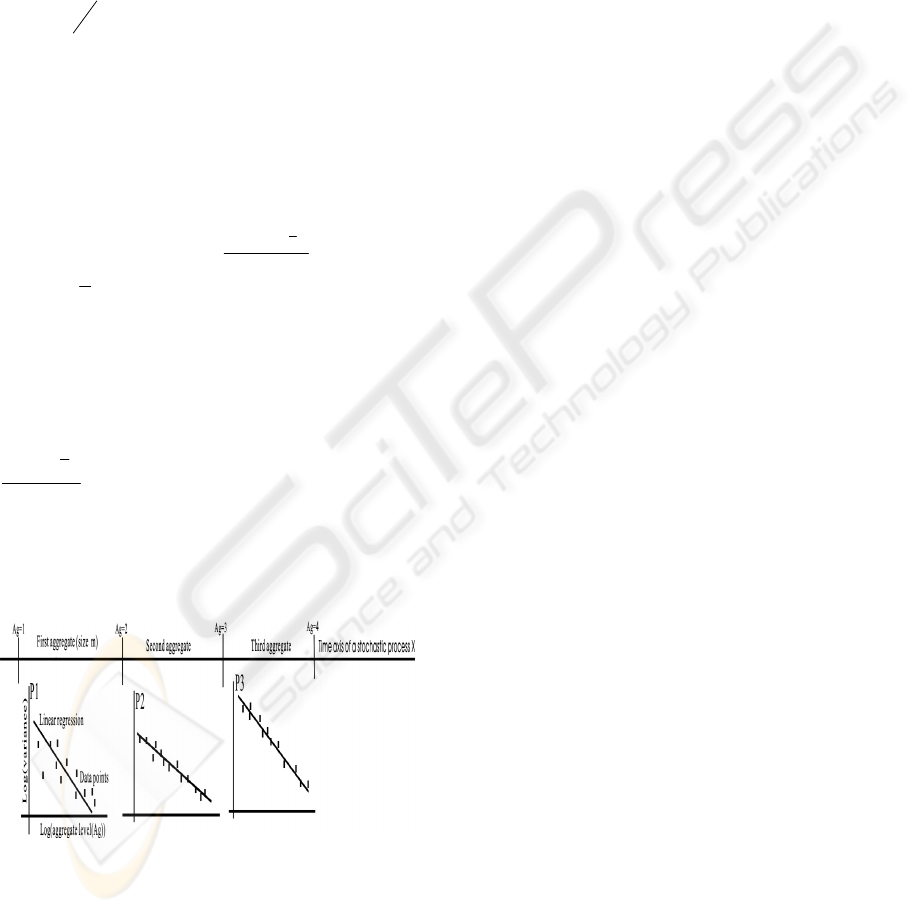
b) these plots yield different

values:

for P1

with

82.0

for P2 with

98.0

, and

for P3 with

95.0

, c) lAg = is the aggregate

level, and d)

9.0

Th , then both P2 and P3

confirms self-similar traffic but not P1 (for

ThR <

). If P2 and P3 yield very

different

values, their H values by

)

−=H

indicate different dimensions or D. The D value may

change over time due to various factors, for

example, the ON/OFF situations in the network

(Willinger, 2003). A changing D or H is a sign of

non-linearity in the stochastic process being

examined. A D/H correlation will be demonstrated,

but the focal discussion of how H or D could affect

system stability will be left out.

Skewness is represented by

(

)

)1( −

−

∑

, where

and

are the measured mean and

standard deviation respectively for the aggregate of

samples. It measures the symmetry of a bell-

shape aggregate distribution. A positive value

indicates that the bell curve skews right and the right

tail is heavier than the left one. Kurtosis is

represented by

)1(

)(

−

∑

−

, and its value decides whether the bell curve is

peaked (for positive value) or flat (or negative value)

compared to the normal distribution with

3=kurtosis

and

skewness

Figure 2: The “aggregate based (AB)” approach

4 EXPERIMENTAL RESULTS

The

S filter was verified by simulations based on

the CAB approach. The experiments were

conducted on the stable Aglets mobile agent

platform, which is designed for Internet applications.

The Aglets makes the experimental results scalable

for the open Internet. The setup for the experiments

is shown in Figure 3, in which the driver and server

are both aglets (agile applets). The driver picks a

known waveform or a pre-collected IAT trace that

may embeds different traffic patterns over time. The

pick simulates the IAT among the requests that enter

the server queue. The FLC dynamic buffer size tuner

is the test-bed for the

S filter. It adjusts the buffer

size on the fly by leveraging the current queue

length, buffer length, and detected traffic pattern.

The traffic pattern(s) that drives the IAT is also

recorded by the E-RTPD that has included the

filter. This helps matching the FLC control behavior

with the specific traffic pattern. The VTune

measures the E-RTPD's average execution time so

that its contribution to time-critical applications on

the Internet can be evaluated. Experiments with

different IAT traffic patterns were carried out. The

results conclude that the

S filter indeed detects

self-similar traffic and helps the FLC deliver more

accurate dynamic buffer size tuning. The

experimental results presented here include: self-

similarity detections, traffic and FLC accuracy, and

D/H correlation.

Table 1 summarizes seven of the many different

simulations conducted. The self-similar traces,

which simulate the inter-arrival times (IAT) for the

request into the server’s buffer being controlled by

the FLC (Figure 3), are generated by using the

Kramer’s tool (Kramer, 2002). The useful

information from the Table 1 summary is listed as

follows:

The

S filter always detect and recognizes self-

similarity in the IAT traffic as long as the network

loading or utilization

is 50% (i.e. 0.5 simulated

by the same tool) or less.

is proportional to the self-similarity dimension

(explained later with Figure 9). For

4.0>

the

traffic self-similarity scales differently as indicated

Figure 5 and 6. Our analysis indicates that this is

possibly the beginning of non-linear scaling or a

sign of possible multifractal traffic. Both Figure 5

and 6 work with

9.0

Th .

The scaling exponent H (Hurst effect) changes with

, which is inversely proportional to the IAT

length that is the “reduction/resolution” in light of

traffic. For

4.0

≤

the scaling is basically the

same (i.e. a monofractal sign). The

value in

ICETE 2005 - GLOBAL COMMUNICATION INFORMATION SYSTEMS AND SERVICES

every case (row) in Table 1 is the average of several

aggregates for the same stochastic process X.

The kurtosis and skewness are different for the

different self-similar traces. Nevertheless they

always indicate the presence of a bell curve.

Figure 3: Setup for the

S filter experiments

Figure 4: Kurtosis and skewness measurements

Figure 5:

S filter yields slope = -0.6809(β = 0.6809),

= 97.74% for

2.0=

Figure 6:

S filter yields slope = -0.4685(β = 0.4685),

= 95.97% for

5.0

Figure 7: Faster convergence of the FLC+

S filter than

the FLC working alone

Figure 8: Less MD deviation by FLC+

S than the FLC

alone

A NOVEL REAL-TIME SELF-SIMILAR TRAFFIC DETECTOR/FILTER TO IMPROVE THE RELIABILITY OF A

TCP BASED END-TO-END CLIENT/SERVER INTERACTION PATH FOR SHORTER ROUNDTRIP TIME

Figure 9: D/H correlation for Table 1

The kurtosis and skewness values for each case

(row) in Table 1 are plotted for comparison (Figure

4). These values are obviously affected by the

loading. When the loading is high (e.g. 60% and

70%) the bell curve tends to skew less but still to the

right. Meanwhile the bell curve tends to get flatter.

Comparatively the skewness of the bell curves for

the seven simulation cases in Table 1 are less than a

Weibull (

5.1=gamma ) distribution, which is

relatively more peaked (

5.4≈kurtosis

). The trend-

lines in Figure 7 for the IAT traffic trace in Figure 5

shows that the “

SFLC + filter” combination

converges much faster to given steady state than the

FLC working alone. With help from the

S filter

the FLC adjusts the GP value for the derivative (D)

control element on the fly according to the currently

detected self-similarity. As a result it produces less

MD than the FLC working alone (Figure 8). In the

experiments the FD3 tool (Sarraille, 2004), which

confirms if an image (e.g. a time series generated by

the Kramer’s tool) is really fractal and measures its

dimension D, was used. The purpose is to evaluate

the D/H correlations (Peitgen, 2004). This

correlation for Table 1 is plotted and shown in

Figure 9. It shows that if D changes suddenly, H also

rescales accordingly to indicate possible traffic

nonlinearity. In contrast, if H scales linearly, it is a

sign of monfractal traffic. The intrinsic average

S filter execution time as observed from all the

experiments is 1455 clock cycles as measured by the

Intel’s VTune Performance Analyzer. It is intrinsic

because it works with immediately available data

(without any actual IAT delay) in a trace. For a

platform of 100 mega hertz the corresponding

physical time is

)10*100/(1455

or 14.55 micro

seconds. In real-life applications the

S filter has to

collect enough IAT samples on the fly before

computing

. This sampling latency can be

significant, and therefore the success of

S filter

application depends of choosing size

for the

aggregate correctly. For example, if the average IAT

is one second,

1000

means 1000 seconds. On

the contrary for the same size

and mean IAT of 1

ms, the physical time is only one second. Therefore,

the

value for the

S filter Java prototype is a

variable rather than a chosen constant, and the

user/tester should fix the time span

instead of

collecting the fixed

samples on the fly. That is,

the number of samples (i.e.

) in an aggregate

within

depends on the IAT; shorter IAT delays

yield a larger

. Then, the

S filter works

adaptively with the

value decided by the IAT for

the “timed aggregate” based on the chosen T.

5 CONCLUSION

The novel self-similarity (

S ) filter is proposed for

real-time applications. It is based on the

“asymptotically second-order self-similarity”

concept (alternatively called statistical

OSS

OSSS

2 ) for stationary time series. As a

component in the enhanced RTPD or E-RTPD it

helps the FLC dynamic buffer tuner yield more

accurate control by detecting self-similarity in the

IAT traffic. This means improved reliability for the

client/server interaction path and shorter roundtrip

time. The

S filter is original because there is no

Table 1:

filter’(log(variance) versus log (aggregate level) to find

)

−=H

(coefficient of determination)

kurtosis skewness

0.6583 0.671 0.956 (95.6%) 0.1 (10%) 0.597045 1.180861

0.6809 0.660 0.975 (97.5%) 0.2 -0.56218 0.798282

0.6425 0.679 0.977 (97.7%) 0.3 0.40215 1.277175

0.6473 0.677 0.972 (97.2%) 0.4 -0.53386 0.861215

0.4685 0.766 0.959 (95.9%) 0.5 -0.58417 0.892037

0.3762 0.812

0.885 (88.5%) (less than

)

0.6 (rejected)

-1.01033 0.446756

0.1978

0.901

0.605 (60.5%)

0.7 (rejected)

1.16043

0.388599

ICETE 2005 - GLOBAL COMMUNICATION INFORMATION SYSTEMS AND SERVICES

100

previous examples in the literature that can detect

self-similarity in a time series on the fly. The next

step in the research is to perfect the CAB approach

by enabling it to determine the range of aggregate

size

that can produce accurate traffic detection

but without any unnecessary and significant latency

in the process.

ACKNOWLEGEMENT

The authors thank the Hong Kong PolyU and the

Department of Computing for funding the RTPD

research with grants APG51 and HJZ91.

REFERENCES

S. Arvotham, R. Riedi and R. Barabniuk, Connection-

Level Analysis and Modeling of Network Traffic,

Proc. of the IEEE/ACM Internet Measurement

Workshop, 2001

B. Braden et al., Recommendation on Queue Management

and Congestion Avoidance in the Internet, RFC2309,

April 1998

L. Cottrel, M. Zekauskas, H. Uijterwaal, and T.

McGregor, Comparison of Some Internet Active End-

to-End Performance Measurement Projects,

http://www.slac.stanford.edu/comp/net/wan-

mon/iepm-cf.html, 1999 Intel’s VTune Performance

Analyzer,

http://ww.intel.com/support/performancetools/vtune/v

R. Jain, The Art of Computer Systems Performance

Analysis – Techniques for Experimental Design,

Measurement, Simulation, and Modeling, Wiley, 1992

Kramer, Generator of Self-Similar Network Traffic,

http://wwwcsif.cs.ucdavis.edu/~kramer/code/trf_gen1.

html

S.M. Lewandowski, Frameworks for Component-based

Client/Server Computing, ACM Computing Surveys,

30(1), March 1998, 3-27

Wilfred W. K. Lin, Richard S.L. Wu Allan K. Y. Wong,

and Tharam S. Dillon, A Novel Real-Time Traffic

Pattern Detector for Internet Applications, Proc. of the

Australasian Telecommunication Networks and

Applications Conference, Sydney, Australia

(ATNAC’04), Dec 2004, 224-227

Wilfred W. K. Lin, Allan K. Y. Wong, and Tharam S.

Dillon, A Novel Adaptive Fuzzy Logic Controller (A-

FLC) to Reduce Retransmission and Service

Roundtrip Time for Logical TCP Channels over the

Internet, Proc. of the EU2004 Conference, August

2004, Japan, 942-951

A. Medina, I. Matta and J. Byers, On the Origin of Power

Laws in Internet Topologies, ACM SIGCOMM, 30(2),

2000, 18-28

Wilfred W. K. Lin, Allan K. Y. Wong, and Tharam S.

Dillon, A Novel Fuzzy-PID Dynamic Buffer Tuning

Model to Eliminate Overflow and Shorten the End-to-

End Roundtrip Time for TCP Channels, Lecture Notes

in Computer Science, Springer Verlag LNCS

Electronic Journal,

http://www.springerlink.com/index/VF155CH38XFL

LB4H

S. Molnar, T.D. Dang and A. Vidacs, Heavy-Tailedness,

Long-Range Dependence and Self-Similarity in Data

Traffic, Proc. of the 7

Int’l Conference on

Telecommunication Systems, Modelling and Analysis,

Nashville, USA,18-21, 1999

H.O.Peitgen, H.Jurgens, D.Saupe, Chaos and Fractals:

New Frontiers of Science 2

edition, Springer, 2004,

pp.686

J. Sarraille and P. DiFalco, FD3,

http://life.bio.sunysb.edu/morph/fd3.html

M.S. Taqqu, Fractional Brownian Motion and Long-

Range Dependence, in Theory and Applications of

Long-Range Dependence, P. Doukhan et al., Eds.,

Birkhuser 2003, 5-38

W. Willinger, V. Paxson, R.H. Hiedi and M.S. Taqqu,

Long-Range Dependence and Data Network Traffic,

in Theory and Applications of Long-Range

Dependence, P. Doukhan et al., Eds., Birkhuser 2003,

373-408

Allan K.Y. Wong and Joseph H.C. Wong, A Convergence

Algorithm for Enhancing the Performance of

Distributed Applications Running on Sizeable

Networks, The International Journal of Computer

Systems, Science & Engineering, vol. 16, no. 4, July

2001, 229-236

Allan K.Y. Wong, Wilfred W.K. Lin, May T.W. Ip and

Tharam S. Dillon, Genetic Algorithm and PID Control

Together for Dynamic Anticipative Marginal Buffer

Management: An Effective Approach to Enhance

Dependability and Performance for Distributed Mobile

Object-Based Real-time Computing over the Internet,

Journal of Parallel and Distributed Computing (JPDC),

vol.62, Sept. 2002, 1433-1453

A NOVEL REAL-TIME SELF-SIMILAR TRAFFIC DETECTOR/FILTER TO IMPROVE THE RELIABILITY OF A

TCP BASED END-TO-END CLIENT/SERVER INTERACTION PATH FOR SHORTER ROUNDTRIP TIME

101