A PRELIMINARY EXPLORATION OF STRIPED HASHING
A probabilistic scheme to speed up existing hash algorithms
George I. Davida, Jeremy A. Hansen
Center for Cryptography, Computer and Network Security
University of Wisconsin - Milwa
ukee, 3200 N. Cramer Street, Milwaukee, WI, 53211 USA
Keywords: hashing, MD5, probability
, SHA, striping.
Abstract: Hash algorithms generate a fixed-size output from a variable-size input. Typical algorithms will process
every byte of the input to generate their output, which, on a very large input, can be time consuming. The
hashes’ potential slowness, coupled with recently reported attacks on the MD5 and SHA-1 hash algorithms,
prompted a look at hashing from a different perspective. By generating several “striped” hashes, we may
speed up the hash verification by a factor of the chosen stripe size.
1 INTRODUCTION
When an executable program is replaced with
malicious code, the new contents will vary
dramatically from the original file. File integrity
monitoring programs like Tripwire use MD5 and
other cryptographic hash algorithms to detect the
smallest change in an executable (or other) file,
down to single bit inversions. When an MD5 hash is
calculated for the file, the entire file is read in and
sent through the algorithm in 512-byte blocks.
These blocks are taken from the file sequentially and
processed until the end of the file is reached. The
technique described by this paper achieves one
primary goal: decrease the time necessary to check
the MD5 hash for large inputs by reducing the
amount of data that is verified in each check.
The primary motivation for this scheme is a
syste
m currently in development that frequently
checks the integrity of running processes.
Calculating a complete hash of the processes’
memory spaces requires too much time, and causes
the system to slow down unnecessarily. The system
needs to be able to verify the integrity of a process,
even if it is only a partial verification, without
disrupting the standard operation of the computer.
2 THE ALGORITHMS
The concept behind the proposed algorithms is
partial hashing, which uses a subset of the input
bytes to generate the cryptographic hash. The
strength of the hash algorithm now depends on the
original algorithm as well as which bytes of the
input are chosen – an unwise choice can allow an
attacker to dodge the integrity checking altogether.
The chosen bytes should be distributed evenly across
the length of the input, so that any string of unused
bytes is of the minimum possible length.
Other algorithms use partial hashing to validate
the accuracy of individual
blocks of a file. Peer-to-
peer networks use these, for example, when each
party may only have a small part of a large shared
file, but needs to know if the blocks they currently
possess are legitimate. Implementations like THEX,
which use Merkle Hash Trees, organize these single-
block partial hashes as the leaves of a binary tree,
and then concatenate the leaf hashes to generate
intermediate hashes. These intermediate hashes are
in turn concatenated, until the root of the tree is
reached, at which point a single hash value is
returned. One of the benefits of hash trees is that the
verifying entity need only know a handful of
intermediate hashes to verify the blocks. There is a
drawback to the typical use of hash trees in that the
data being hashed (at the leaves of the tree) is in
contiguous blocks. If an attacker can replace a
single block such that the replacement hashes to the
same value as the original, the whole file can be
corrupted.
2.1 p-striped Hashing
The following algorithm is used in the interest of
choosing a subset that, instead of being blocks of
363
I. Davida G. and A. Hansen J. (2005).
A PRELIMINARY EXPLORATION OF STRIPED HASHING - A probabilistic scheme to speed up existing hash algorithms.
In Proceedings of the Second International Conference on e-Business and Telecommunication Networks, pages 364-367
DOI: 10.5220/0001414003640367
Copyright
c
 SciTePress

contiguous data, is evenly distributed over the entire
input. Given the length L of the input file, a small
number p is chosen such that p < L. A buffer of size
⎣L / p⎦ is allocated and filled, one byte at a time,
with bytes from the file at locations (p * i), where
i = 1 to ⎣L / p⎦. Finally, the hash of this buffer is
computed and stored as the p-striped hash.
The effect of this algorithm is that the hash
function only processes every p
th
byte in the file.
Therefore, any changes to the file, to remain
undetectable by the modified hash algorithm, would
have to be made in the gap of p-1 bytes between
samples. Assuming that he knew the value of p, an
attacker could work around this partial hashing by
only modifying bytes unchecked by the striped hash.
For example, if L is 30K, p may be set to 17. A
buffer of size 4388 is allocated to hold the pre-
processor’s output. This buffer is then filled with
the bytes found at 17, 34, 51, and so on – all
multiples of p – until it is completely filled. This
data is passed to the hash algorithm which produces
a cryptographic hash whose generation time is
roughly 17 times faster than the calculation of a hash
of the complete file.
This algorithm is not particularly useful on its
own. Instead, the variants that follow use the basic
ideas of the p-striped hash but are more effective.
For example, the probability that x randomly
selected contiguous corrupt bytes of the input will be
detected by this basic partial hash is only x/p. For a
p large enough to yield substantial speed gains, the
probability of detecting a modification is
unacceptably low. Algorithms that increase this
probability are described below.
2.2 p-offset-striped Hashing
Using p-striped hashing as a base, p-offset-striped
hashing adds extra “parallel” hashes by slightly
offsetting the initial position of the stripe. The
original p-striped hash is stored with those of the
offset p-striped hashes. Instead of the marginal
performance gains of a small p, this new algorithm
allows the choice of a larger p with some additional
obstacles to an attacker.
The concatenation of two such hashes could
create a hash twice as long as the typical output for
the hash algorithm. Thus, a p-offset-striped MD5
with one offset hash will generate 32 bytes of hash,
the first 16 bytes being the p-striped hash, the
second half being the offset hash. Instead of
checking both the original and the offset hashes at
the same time to ensure integrity, only one is
checked at a time to determine if a change has been
made. The hash value to verify will be chosen
randomly at the time the check is made. The
assumption made in this case of precomputing
multiple hashes is that the system verifying the
hashes will do its verification frequently enough to
ensure that it is checking both the p-striped and any
available offset hashes on a regular basis. The
decision to precompute more partial hashes becomes
a choice of how much storage space to exchange for
the speed and security of the extra hashes.
The offset, s, is chosen such that it is less than p
but not a divisor of p. A buffer of size ⎣L / p⎦ is
allocated, as with the standard p-striped hashing, and
is filled a byte at a time with data from the file at
locations
((p * i) + s) mod L
As in p-striped hashing, i ranges from 1 to ⎣L / p⎦.
Note that it is possible for a stripe to “wrap” back to
the beginning of the input given a large enough
value of s.
Choosing a variety of values for s generates
multiple parallel striped hashes. A convenient way
of generating a handful of values of s is to divide p
into equal pieces depending on how many hashes are
desired. If n hashes are desired, s can be calculated
as
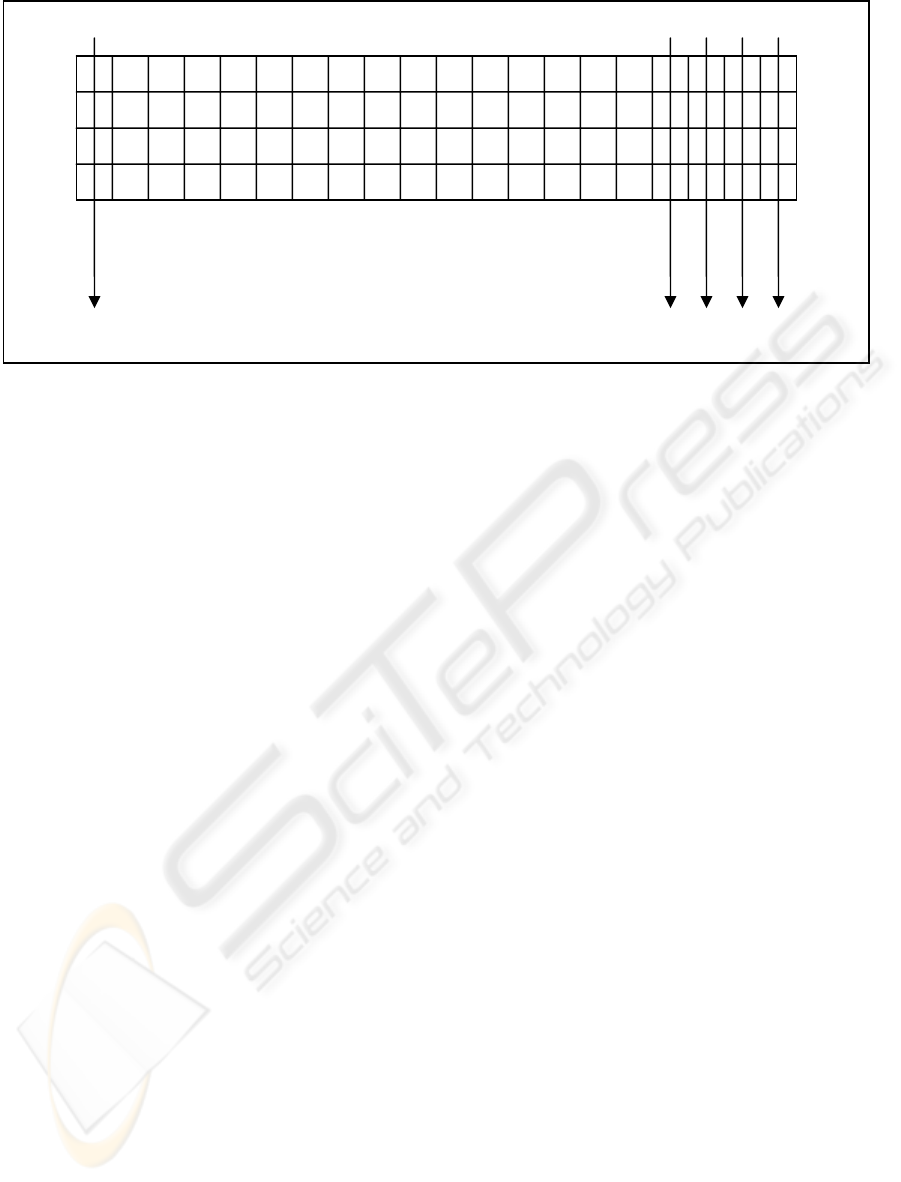
Hash 20 Hash 1 Hash 2 Hash 3 Hash 4
Figure 1: An 80-byte file with complete 20-striped offset hashing
ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS
364

s = ⎣j * (p / n)⎦
where j ranges from 0 to n-1. These values for s are
spread out evenly between 0 and p, so the length of
the gaps between what the offset hashes cover is
minimized. The first hash corresponds to the p-
striped hash, while the remaining hashes are offset.
For example, if eight hashes (that is, n = 8) that are
spread out evenly over the input are desired, and p is
101, values for s are calculated as 0, 12, 25, 37, 50,
63, 75 and 88.
In this scheme, pre-processing the input will
speed up the hash checking by a factor of p and the
calculation of the initial hashes by a factor of p/n.
Verifying each of these hashes will take
approximately the same amount of time since the
number of input bytes for each stripe is the same.
The probability that x randomly selected
contiguous corrupt bytes of the input will be
detected by the p-offset striped hash with n offsets
and s generated as described above is nx/p. This
corresponds to the same probability as if a stripe size
of p/n was chosen, and the maximum gap size is
⎡p/n⎤ - 1. The probability that a single randomly
selected hash from this collection of offset hashes
will detect these corrupt bytes is x/p, like the basic p-
striped hash.
This preprocessing algorithm weakens the
underlying cryptographic hash algorithm, since the
collection of hashes is now vulnerable to collisions.
An attacker knowledgeable of the values of p and s
could generate two inputs that produce the same
collection of striped hashes. This weakness is
eliminated with the following algorithm.
2.3 Complete Striped Hashing
If p is chosen properly with respect to L, a hash
algorithm could be devised that leaves no gaps in the
input and outputs a complete p-striped hash. That is,
the algorithm will process every byte of the input
file, but still have a tremendous improvement in
speed. If p and L are relatively prime, a scheme
similar to that of p-offset hashing can be used to
generate the striped hashes. A buffer is filled with
bytes from locations
(p * i) mod L
where i ranges from 1 to ⎣L / p⎦, but only for the first
partial hash. A second buffer is then filled with
bytes according to the above formula where i ranges
from ⎣L / p⎦ + 1 to ⎣2 * L / p⎦. Separate buffers
continue to be filled until the p
th
buffer is filled with
similar bytes, when i ranges from ⎣(p-1) * L / p⎦ + 1
to ⎣ p * L / p⎦. Each of these buffers is passed to the
hash algorithm separately, yielding p partial hashes.
This preprocessing will assign each of the L bytes of
the file to one of the hashes. Any single-byte change
to the file will be detected by one of the generated
hashes. Thus, the probability that any change in the
file will be detected by at least one of the hashes is
1. “Adjacent” hashes will detect contiguous
modified bytes. The probability that any single hash
will detect an x byte contiguous change to the file is
x/p.
The p-offset hashing scheme can also be used to
generate a “complete” set of hashes. With a stripe
size of p, the number of hashes initially computed
(described as n above) is set to the stripe size. Since
n = p, the offsets range from 0 to p-1 and every byte
of the file is covered by at least one hash, as shown
in Figure 1. Any single-byte modification can be
detected by checking all of the given hashes.
However, one of the algorithm’s assumptions, as in
p-offset striped hashing, is that the verification of
randomly chosen striped hashes is performed
frequently. Because of this assumption, the
modified hash algorithm will, with a probability
inversely proportional to p, eventually detect the
modification. Given enough integrity checks, the
modification will eventually be discovered. On
average, it will require p/2x hash verifications to
catch x invalid contiguous bytes in a complete p-
striped collection of hashes.
The decision remains as to how p should be
chosen – should it be large, so there are many
different hashes to check quickly, but lower
probability that a change will be detected? Would it
be more advantageous to choose a smaller value that
detects modifications with a higher probability but
only a marginal speedup?
2.4 p-q-striped Hashing
Instead of choosing an offset from a given p, as in p-
offset striped hashing, a separate p might be chosen,
q. The q-striped hash is generated separately from
the p-striped hash and stored like an offset hash.
With the second stripe of a different length, an
attacker would have to evade every p
th
and every q
th
byte. The probability that x randomly selected
contiguous corrupt bytes will be detected by one or
both hashes of a p-q-striped hash is
(px + qx – x2) / pq
The probability that the invalid bytes are detected in
a single check of one of the hashes, chosen
randomly is
(px + qx) / 2pq
p-q-striped hashing could be expanded to include
even more values of p, so that a p
1
-p
2
-…-p
n
-striped
hash could be constructed, depending on how many
A PRELIMINARY EXPLORATION OF STRIPED HASHING: A probabilistic scheme to speed up existing hash
algorithms
365

hash choices are desired. A similar statistical
analysis as above could be done with three hashes to
determine the probability that one or more of the
hashes detects a contiguous block of corrupt data.
This probability is
(x
3
– x
2
(p
1
+p
2
+p
3
) + x(p
1
p
2
+p
2
p
3
+p
1
p
3
)) / p
1
p
2
p
3
Similarly, on average, the probability that a single
pass of one randomly chosen striped hash will detect
the x corrupt bytes is
x(p
2
p
3
+ p
1
p
2
+ p
1
p
3
) / 3p
1
p
2
p
3
The probabilities of detection for four or more
stripes could also be calculated in the same way.
Generating the full baseline hash for a file of
length L requires processing of all L bytes. To fully
verify the hash of the same file at a later time will
require the same amount of processing, as the length
of the input will be the same. The p-q-striped hash
scheme, however, will only require
⎣L / p⎦ + ⎣L / q⎦
bytes to be hashed to generate the two partial
baseline hashes. Checking the integrity of the file
with one of the hashes requires only ⎣L / p⎦ or ⎣L / q⎦
bytes to be passed to the hash algorithm, giving an
average speedup of (p + q)/2, compared to
performing the full baseline hash.
The lengths of the contiguous bytes unchecked
by this algorithm vary from 1 to p-1. The number of
gaps of length 1 is equal to those of length 2, 3, and
so on, up to p-1. This mix of different-length gaps
makes even a knowledgeable attacker’s job of
bypassing the integrity checks extremely difficult.
As with p-offset striped hashing, a “complete”
version of p-q-striped hashing is possible. If p and q
are both relatively prime to L, hashes can be
generated by iterating past the end of the file as
described above in “Complete Striped Hashing”. In
essence, this scheme produces two complete sets of
hashes – the complete p-striped hash and the
complete q-striped hash.
3 REMARKS
One of the original purposes of hashing was to
eliminate the need to store a duplicate copy of the
file (or other input) whose integrity a system needed
to monitor – instead, the hash could be stored. The
proposed system stores more hashes and only looks
at particular parts of the input when doing a single
check. After several such checks, the input can be
validated in an equivalent way to checking the entire
input at once, but having the benefit of spreading the
integrity checking out over a period of time.
The aforementioned preprocessors serve to
speed up existing hash algorithms without
significantly sacrificing security, provided they are
implemented properly. The specific placement of
these cryptographic checks in the security system is
outside the scope of this paper, but is an area of
work-in-progress. This work is in its preliminary
stages and we are continuing to examine the issue of
cryptographic hashing of software and data to
preserve system integrity.
REFERENCES
Chapweske, J. and Mohr, G., 2003. Tree Hash EXchange
format (THEX). http://www.open-content.net
/specs/draft-jchapweske-thex-02.html
Davida, G. and Matt, B., 1985. Crypto-Secure Operating
Systems. In AFIPS Conf. Proc., Nat’l Comp. Conf.
Davida, G., Desmedt, Y., and Matt, B., 1989. Defending
Systems Against Viruses Through Cryptographic
Authentication. In Rogue Programs: Viruses, Worms
and Trojan Horses, Van Nostrand Reinhold. New
York.
Ganesan, P., Venugopalan, R., Peddabachagari, P., Dean,
A., Mueller, F., and Sichitiu, M., 2003. Analyzing and
Modeling Encryption Overhead for Sensor Network
Nodes. In Proc. 2
nd
ACM Int’l Conf. Wireless Sensor
Networks & Appl.
Hansen, J., 2005. Cryptographic Authentication of
Processes and Files to Protect a Trusted Base.
Unpublished Master’s thesis, University of Wisconsin,
Milwaukee.
Kaminsky, D., 2004. MD5 To Be Considered Harmful
Someday. http://www.doxpara.com/md5_someday.pdf
Kim, G. and Spafford, E., 1994. The Design and
Implementation of Tripwire: A File System Integrity
Checker. In Proc. 2
nd
ACM Conf. Comp. and Comm.
Security.
Menezes, A., van Oorschot, P., and Vanstone, S., 2001.
Handbook of Applied Cryptography, CRC Press. Boca
Raton, FL, 5
th
Printing.
Naor, M. and Yung, M., 1989. Universal One-Way Hash
Functions and their Cryptographic Applications. In
Proc. 21
st
Ann. ACM Symp. Theory of Comp.
Schneier, B., 1996. Applied Cryptography, John Wiley
and Sons, Inc. New York, NY, 2
nd
Edition.
Touch, J., 1995. Performance Analysis of MD5. In Proc.
ACM SIGCOMM ’95 Conf. Appl., Tech., Arch., &
Prot. for Comp. Comm.
ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS
366