A PRICING MODEL OF GPRS NETWORKS WITH WI-FI

INTEGRATION FOR “HEAVY” DATA USERS

Saravut Yaipairoj, Fotios Harmantzis, Vinoth Gunasekaran

Stevens Institute of Technology

Hoboken, NJ USA

Keywords:

Wireless Pricing, Incentive Compatible, Network Integration, 3G-like services, Self-differentiation, GPRS,

Wi-Fi.

Abstract:

As wireless services have become increasingly integrated and their demand is mounting, Wi-Fi provides an

appealing opportunity for the GSM/GPRS operators to enhance their data capability. By integrating both

networks, operators are able to provide 3G-like services. However, both networks have different data rates

and capacity, which makes pricing a challenging issue. In this paper we propose a pricing model for GPRS

networks integrated with Wi-Fi, which applies to data users with high service demand (“heavy”). Through op-

timization technique, our proposed model identiﬁes how the integration can play a signiﬁcant role in increasing

operators’ overall revenue and potentially improving the performance of GPRS networks.

1 INTRODUCTION

As wireless technologies have been emerging and im-

proving, the boundary of their applications becomes

blur. The wireless technologies, which once posi-

tioned for their own speciﬁc applications, now can

provide comparable services. For certain wireless ser-

vices, technologies being used for different applica-

tions can now be seen as alternative solutions. The ob-

vious examples are the improvement in mobility and

coverage of Wi-Fi and the increasing capacity of data

services in cellular networks. Wi-Fi has been both a

competing and a complementary technology to cellu-

lar networks (Salkintzis, 2002; Ahmavaara, 2003). It

offers fast connectivity and relatively much cheaper

services compared to 2.5G cellular networks, such as

General Packet Radio Service (GPRS). However, cov-

erage of cellular networks is much larger than that

of Wi-Fi networks. Several GPRS operators con-

sider providing Wi-Fi services along with their net-

works in order to improve their networks’ capacity

and alleviate congestion in GPRS networks. As a re-

sult, the main challenge that they would encounter is

the pricing issues of services in both networks. Tra-

ditionally, GPRS networks offer simple usage-based

pricing (Courcoubetis, 2000) for each megabyte that

users transmit over the network. On the other hand,

Wi-Fi service providers ﬁnd it more difﬁcult to come

up with a pricing plan for their service. There are

several payment options, such as a subscription fee

on monthly basis, a one-time charge per connection,

or usage-based pricing. The pricing schemes vary

among different service providers. However, most

Wi-Fi charges are based on ﬂat pricing (Anania, 1997;

boingo) such as a connection fee, which the network

charges a user per connection in one location. To alle-

viate this pricing confusion in both networks, cellular

operators have an option to integrate their networks

with the hotspots and provide a common bill to their

customers. In addition, data access over Wi-Fi is cost

effective compared to cellular networks. A cellular

base station costs over 30 times more than a Wi-Fi

hotspot (Salkintzis, 2002). Network operators would

enjoy signiﬁcant cost saving while offering broad-

band wireless services that are comparable to 3G,

namely, 3G-like services (Ahmavaara, 2003; Doufexi,

2003). With the integration of both networks, network

users, especially the ones with high service demand

(or heavy users), will be able to choose to transmit

data over either GPRS networks, (which offer wide

coverage but costly and limited transmission rate), or

Wi-Fi networks (which offer cost-effective services

and high transmission rate but limited coverage).

Network users are inherently price sensitive (Ma-

son, 1995). Using prices, the network can signal to

users, providing incentives, which inﬂuence their be-

Yaipairoj S., Harmantzis F. and Gunasekaran V. (2005).

A PRICING MODEL OF GPRS NETWORKS WITH WI-FI INTEGRATION FOR “HEAVY” DATA USERS.

In Proceedings of the Second International Conference on e-Business and Telecommunication Networks, pages 80-85

DOI: 10.5220/0001414800800085

 SciTePress

havior to choose the networks that meet their pricing

criteria (Falkner, 2000). The fact that users choose to

access networks based on prices is similar to the con-

cept of Paris Metro Pricing (PMP) (Odlyzko, 1999).

That is, the GPRS operators could promote self-

differentiation by charging different prices on those

two networks. Pricing incentive would likely to move

the network users from the congested high-priced

GPRS networks to the less congested inexpensive Wi-

Fi networks. However, PMP networks are identi-

cal networks with different prices charged to users.

GPRS and Wi-Fi networks are different in terms of

capacity and coverage. Clearly, integration between

the two networks will make the pricing problem chal-

lenging.

In this paper, we propose a simple but effective

demand-based pricing model for the integration be-

tween GPRS and Wi-Fi networks. In Section 2,

we describe the architectural overview of Wi-Fi in-

tegrated with GPRS. In the third section we propose

our optimized pricing model, followed by Section 4

where we present the results of our numerical analy-

sis. We draw our conclusions in Section 5.

2 ARCHITECTURAL OVERVIEW

OF INTEGRATION: Wi-Fi WITH

GPRS NETWORKS

Integrating GPRS and Wi-Fi gives both ubiquitous

coverage and support high data rate in strategic lo-

cations (schools, ofﬁce, airports, hotels, coffee shops

etc.). If both Wi-Fi and GPRS networks are integrated

then cellular operators are able to meet some require-

ments for 3G services. This would allow them to pro-

vide high quality data services which can be perceived

as 3G-like services. The following are two types of

integration, tight coupling architecture and loose cou-

pling architecture (Salkintzis, 2002; Oliver, 2002).

2.1 Tight Coupling architecture

In this type of architecture the Wi-Fi is connected

to the GPRS network as an alternative Radio Ac-

cess Network (Salkintzis, 2002). It is connected to

the operator’s core network. The hotspot can reuse

the GPRS infrastructure like core network resources,

subscriber databases and billing systems. The mobile

users can select their network preferences or choose

to get connected at the best available network speed.

This is all done in software and will automatically

connect them to the network of their choice. Fig. 1

illustrates the tight coupling architecture for the inte-

grated network.

MS

GPRS

RAN

GPRS Core

External Packet Data

Network

WLAN

SGSN

GGSN

HLR

SGSN

Figure 1: Tight coupling architecture for GPRS integrated

with Wi-Fi networks.

2.2 Loose Coupling Architecture

The hotspots are coupled with the GPRS network in

the operator’s IP network. So the Wi-Fi data traf-

ﬁc goes directly to the operator’s IP network, instead

of going via the GPRS core network (Oliver, 2002).

Though the Wi-Fi and cellular networks remain sep-

arate, there is a common platform for authentication,

accounting and authorization. The hot spot may be

owned by any third party carriers with roaming en-

abled via a dedicated connection between the cellular

operators and Wi-Fi providers or over an existing In-

ternet. Fig. 2 illustrates the loose coupling architec-

ture for the integrated network.

MS

GPRS

RAN

GPRS Core

External Packet Data

Network

WLAN

SGSN

GGSN

HLR

SGSN

Figure 2: Loose coupling architecture for GPRS integrated

with Wi-Fi networks.

3 PROPOSED PRICING MODEL

In our proposed model, we assume that a user is ini-

tially in the GPRS coverage and he is ready to per-

form a large ﬁle transfer. Users subscribes to both

GPRS and Wi-Fi services. There will be one com-

mon Accounting, Authentication, and Authorization

(AAA) server and billing system maintained by the

cellular operators for all integrated hotspots. Now the

user has two options: he can either perform ﬁle trans-

fer right away over GPRS network paying a higher

price, or he can search for Wi-Fi hot spots, assuming

he regularly crosses Wi-Fi networks. Once users are

in hotspot coverage, different types of hot spots would

determine if users need to pay a roaming fee (third

party hotspot case) or not (operator-owned hotspot

case). We disregard the roaming fee at this point since

ICETE 2005 - WIRELESS COMMUNICATION SYSTEMS AND NETWORKS

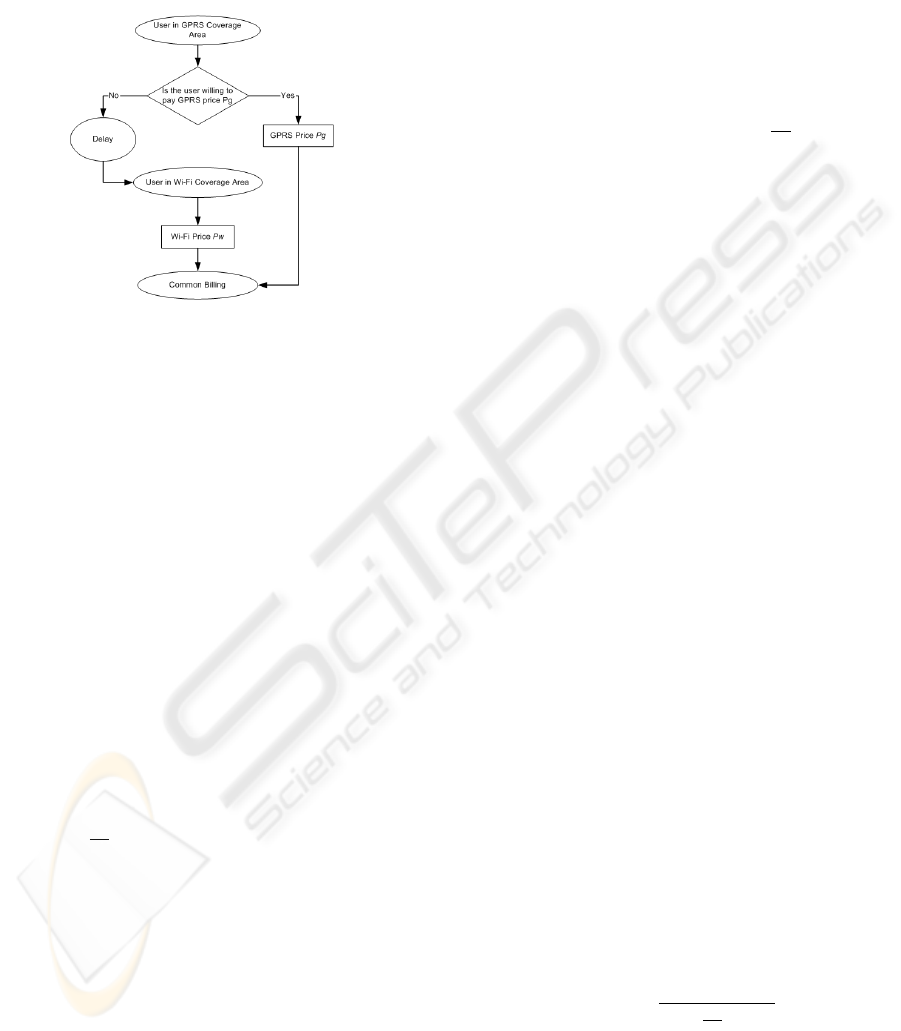
that fee is not signiﬁcant enough to contribute to the

Wi-Fi charges when compared to charges from GPRS

services. Fig. 3 illustrates a blocking diagram for the

scenario we just described.

Figure 3: Pricing Block for GPRS networks with Wi-Fi in-

tegration.

As mentioned earlier, the cost of transmitting data

over a GPRS network is quite high when compared to

Wi-Fi network. This signiﬁcant price difference be-

tween the two networks can inﬂuence the way users

use these networks. Some users may be willing to

search for a Wi-Fi network, if they need to perform

a large ﬁle transfer. Hence, price incentive can inﬂu-

ence users to use either GPRS services with higher

price tag (more convenience since the network has

larger coverage) or Wi-Fi services with lower price.

We argue that the percentage of mobile users D who

accept to be charged by GPRS networks, depends

heavily on the price ratio between the two networks

(Hou, 2001). D can be mostly inﬂuenced by the de-

mand function which is a function that characterizes

the reaction of users to changes in price. In this paper

we use the demand function that appears in (Oldyzko,

2000) since it is used for different classes of users,

that ﬁt our model. The demand function is as follows:

D = e

−(

−1)

, 0 ≤ D ≤ 1, p

≥ p

(1)

where p

is the GPRS charge and p

is the Wi-

Fi charge for each user (p

could be either operator

owned or third party owned hot spot charge). We are

interested in the case when price incentive can inﬂu-

ence decision of users. Therefore, the session volume

charged by GPRS networks must be large enough to

allow p

to be greater than p

. As we know GPRS

pricing is usage-based charges, which do not depend

on holding time but the session volume, therefore, p

is a linear function of the number of megabytes trans-

mitted over the network. For Wi-ﬁ charge, it is based

on ﬂat pricing, which is basically a connection fee.

Therefore, p

and p

can be described as follows:

= r

· v

= r

(2)

where r

is the charging rate per megabyte for the

GPRS network, r

is the connection fee of the Wi-Fi

network, and v is the session volume of data that users

transmit over the GPRS network.

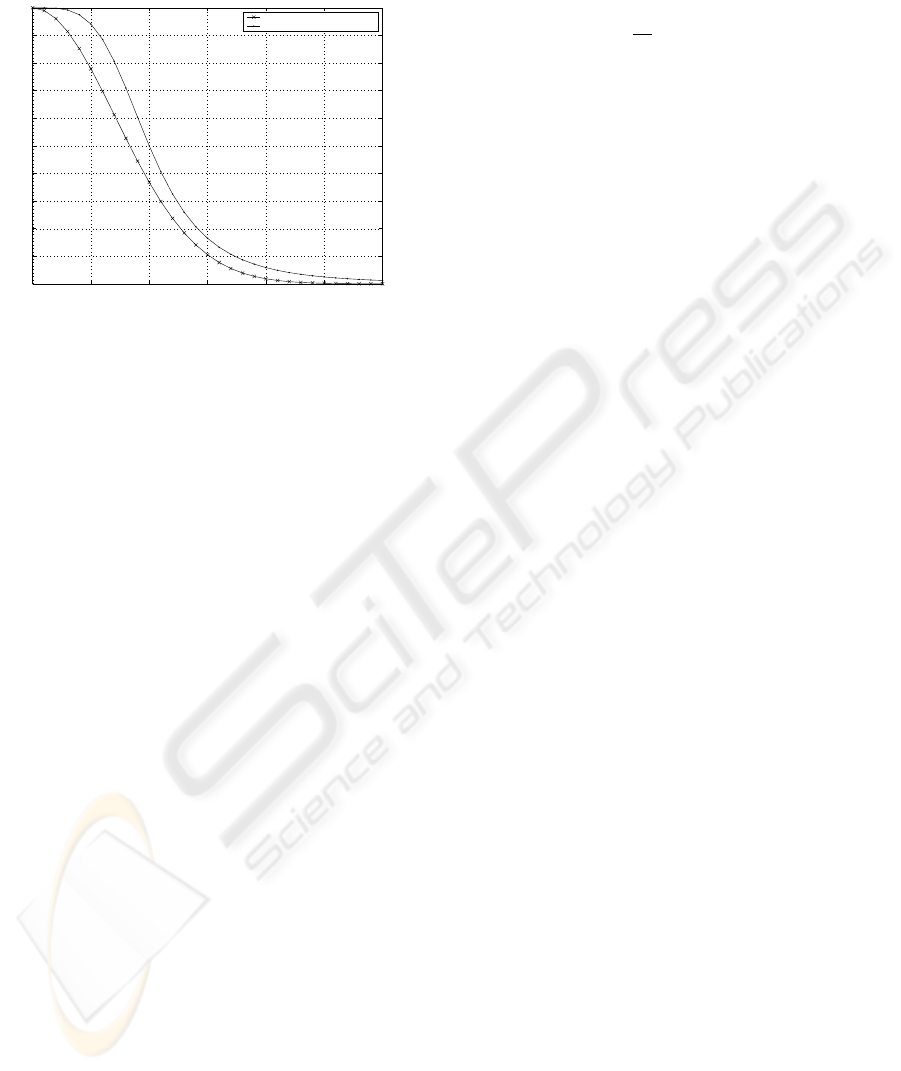
Lower curve in Fig. 4 illustrates the demand func-

tion in (1). The horizontal axis represents the price ra-

tio between GPRS and Wi-Fi charges (

− 1). This

function works quite well in our model because, ﬁrst,

the demand function begins high for small price ratio

representing the situation when users have small vol-

ume of data to transmit. The price charged by GPRS

networks would not be much different from the Wi-

Fi charge. The users have little incentive to seek for

Wi-Fi hotspots resulting in the high user demand for

GPRS usage. Then, the demand decreases rapidly as

the curve gets into a mid-range and has very narrow

tail. This part of the curve represents the increase in

GPRS charges due to the increasing session volume

from users. There is enough incentive for some users

to start migrating to Wi-Fi resulting in the reduction of

GPRS usage. For example, when the price difference

at the horizontal axis equals to one, the GPRS charge

is double the Wi-Fi charge, resulting in the GPRS de-

mand dropping to 36.79 percents.

The revenue due to integration can be determined

by the weighted sum of the revenue created by the

GPRS networks and Wi-Fi networks based on their

corresponding demand. Therefore, from equation (2),

the average revenue of the integrated network can be

determined as follows:

int

= D · (r

· v) + (1 − D) · r

(3)

Regarding the revenue gained from GPRS network

without Wi-Fi integration, the GPRS users do not

have an alternative to migrate their trafﬁc. Therefore,

the demand of users using non-integrated GPRS net-

works would be higher than equation (1). Since the

distribution of session volume in GPRS networks is

not available to us, we have to come up with a mean-

ingful demand function. This function needs to be

well above the demand function in equation (1), to

represent the higher demand of GPRS networks in the

absence of Wi-Fi. The demand function can be shown

as follows (Oldyzko, 2000):

w.o.int

1 + (

− 1)

(4)

where K is a constant. In our case, we set K equal

to p

for the purpose of ﬁtting our demand curve ac-

cording to our assumptions. That, does not mean that

w.o.int

depends on the Wi-Fi charge. By compar-

ing the revenue generated in both cases, we can gain

A PRICING MODEL OF GPRS NETWORKS WITH WI-FI INTEGRATION FOR “HEAVY” DATA USERS

some ideas about the effect of integration on the rev-

enue stream. Fig. 4 illustrates both demand functions.

0 0.5 1 1.5 2 2.5 3

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

User demand of GPRS networks (D)

Price ratio between GPRS and Wi−Fi ((P

)−1)

GPRS with Wi−Fi integration

GPRS without Wi−Fi integration

Figure 4: Demand functions.

Based on the user demand for GPRS network with-

out integration, the revenue gained from GPRS net-

work without integration is as follows:

w.o.int

= D

w.o.int

· (r

· v) (5)

In terms of performance improvement of GPRS

networks with Wi-Fi integration, we focus on the por-

tion of users’ demand that we can ofﬂoad to the Wi-ﬁ

network. Each GPRS user generates a certain amount

of session volume based on their perference. We

would need to ﬁnd prices for both GPRS and Wi-ﬁ

networks that attracts users and reduces the their de-

mand down to some target demand D. To be speciﬁc,

we will set up an optimization model to ﬁnd the opti-

mal r

and r

based on target demand D

In our optimization model, we ﬁrst set up our ob-

jective function. The most suitable objective function

would be equation (3) due to the fact that the opti-

mal r

and r

at any target demand should be able

to yield the maximum revenue for the integrated net-

works. The objective function is subjected to cer-

tain constriants which are r

, r

and D. r

and r

must be constrainted based on the competitive market

prices which the network operators should be able to

provide based on their cost analysis of their networks.

For the target demand D, it speciﬁes the portion of

data users who choose GPRS networks for their data

transmission, which represent the network operation

point of GPRS networks. Therefore,we can use D

as the constraint for trafﬁc ofﬂoad to Wi-ﬁ networks.

Hence, we can set up our objective function and its

constraints as follows:

Maximize R

int

(6)

subject to the following constraints

a ≤ r

≤ b

c ≤ r

≤ d

D = e

−(

−1)

= D

where [a, b] and [c, d] are the constraints for r

and

respectively, D

is the target demand of GPRS

users. Regarding average session volume (v), the dis-

tribution of v in GPRS networks with Wi-Fi integra-

tion is required for optimal charges in both networks.

We do not have such distribution at this point. How-

ever, in (Kilpi, 2003), Kilpi illustrates cumulative ses-

sion volume of a large number of GPRS sessions, giv-

ing an overview of typical GPRS sessions. The result

shows that the session volume for very “big” sessions

of GPRS services is hardly more than 5 MB due to

slow user speeds and structural delay of GPRS net-

works. Therefore, we would be interested in some

typical larger sessions (not more than 5 MB) that we

could use pricing mechanism to ofﬂoad them to Wi-Fi

networks. By ofﬂoading the trafﬁc to Wi-Fi, we ex-

pect that the performance of GPRS networks will be

improved signiﬁcantly (it is beyond the scope of the

paper to prove that in a rigorous manner).

4 NUMERICAL ANALYSIS

In this section, we present our preliminary results

based on the numerical analysis. We illustrate the

revenue gained from network integration and the ef-

fect of Wi-Fi connection fee on the average revenue

of the integrated networks. Furthermore, we present

the results from our optimization model which allows

us to setup the optimal prices which yield maximum

revenue at a certain target user demand. The price set-

ting attract GPRS users to migrate and reduce trafﬁc

load in GPRS networks.

4.1 Assumptions and parameters

We consider the case where users want to transmit

relatively big data session, e.g., 1 MB or more. The

large amount of users’ trafﬁc creates pricing incentive

to seek and transmit their trafﬁc onto less expensive

Wi-Fi networks. Smaller session volume (< 1 MB)

will not create enough incentive for users to look for

hot spots. We assume that pricing in GPRS networks

is usage-based at a rate of 6 dollars per megabyte.

Charging at Wi-Fi hot spots is ﬂat, where users are

charged per connection; users can transmit or receive

as much trafﬁc as they want during a connection. In

addition, we assume that users have access to Wi-Fi

hot spots, when they seek for them. The only incen-

tive that drives them to hotspots is pricing. We do not

ICETE 2005 - WIRELESS COMMUNICATION SYSTEMS AND NETWORKS

include the coverage or location of hot spots into our

pricing model.

4.2 Numerical Results

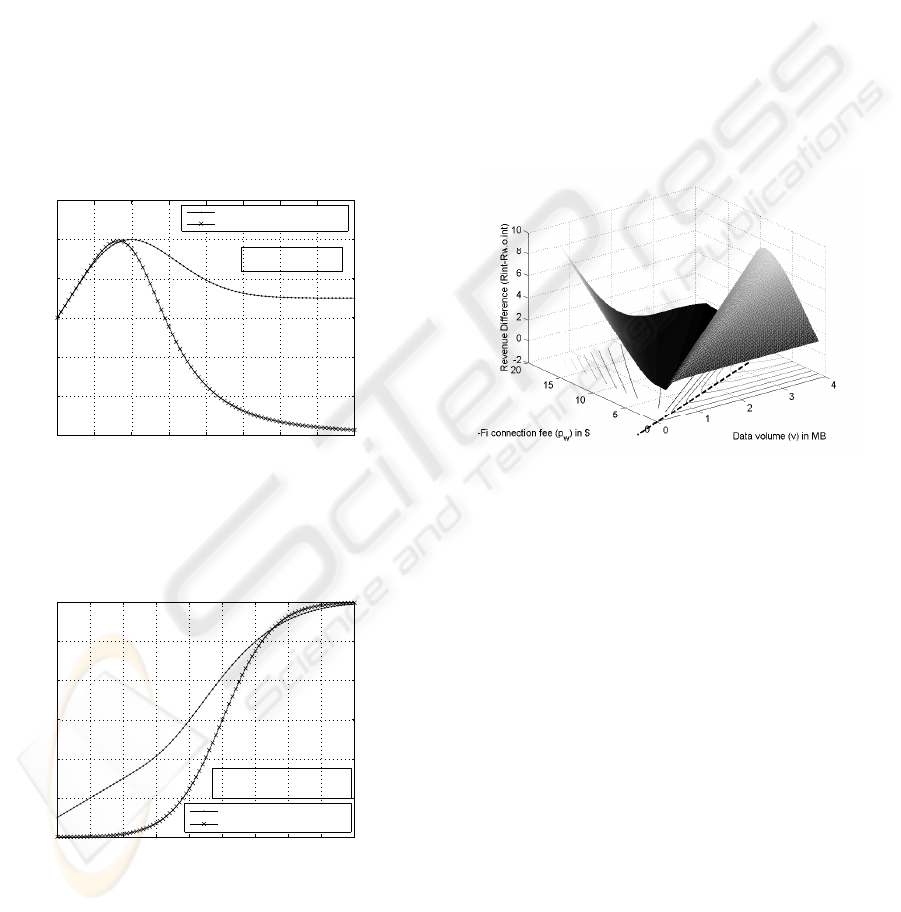
Fig. 5 shows the revenue gained from the integration

of networks determined by equation (3), versus the

average session volume. The Wi-Fi connection fee is

7 dollars per connection, regardless of the amount of

trafﬁc transmission. We can see that when data vol-

ume per connection increases, users would be inﬂu-

enced by price incentive to transmit their trafﬁc over

Wi-Fi hot spots, resulting in additional revenue. How-

ever, the revenue starts to drop at the average usage of

2 MB, since large amount of users would migrate to

inexpensive Wi-Fi hotspots causing reduction in rev-

enue.

1 1.5 2 2.5 3 3.5 4 4.5 5

Average Revenue per connection (R)

Session Volume in MB/connection (v)

GPRS with Wi−Fi Integration

GPRS without Wi−Fi Integration

= $7 per connection

Figure 5: Revenue from GPRS networks with Wi-Fi inte-

gration with respect to average session volume.

1 2 3 4 5 6 7 8 9 10

Average Revenue per Connection (R)

Wi−Fi charging rate(r

)

GPRS with Wi−Fi Integration

GPRS without Wi−Fi Integration

Average session volume is 2

Figure 6: Revenue gained from GPRS and Wi-Fi integration

with respect to the Wi-Fi connection fee.

Fig. 6 shows the average revenue gained from

GPRS integrated with and without Wi-Fi versus r

We assume that each user transmits an average of

1 MB per connection. The result shows that when

increases, the revenue for GPRS with integra-

tion is no longer higher than non-integrated GPRS;

users would continue using the GPRS network due

to high r

; there is no signiﬁcant price incentive for

them to switch to Wi-Fi. We could think of r

that

yields the largest difference between those two rev-

enue curves, which represents the best tradeoff be-

tween revenue and trafﬁc migration. Fig. 7 illus-

trates the revenue difference between equation (3) and

(5) (R

int

− R

w.o.int

) versus r

and v in a three-

dimensional plane. The contour of the plane illus-

trates the line (dash line), where every point on that

line yields the largest difference in revenue and their

corresponding r

and v. For example, at v equals to

2.2 MB, r

equals to 5 dollars representing the largest

difference in the revenue curve.

Figure 7: Difference in Revenue between GPRS integrated

with Wi-Fi and non-integrated GPRS networks.

To ofﬂoad the trafﬁc from GPRS networks to Wi-

Fi, r

and r

must be set appropriately so that the

system yields maximum revenue and attracts GPRS

users to migrate to Wi-Fi networks. Based on our as-

sumption of the demand function and the proposed

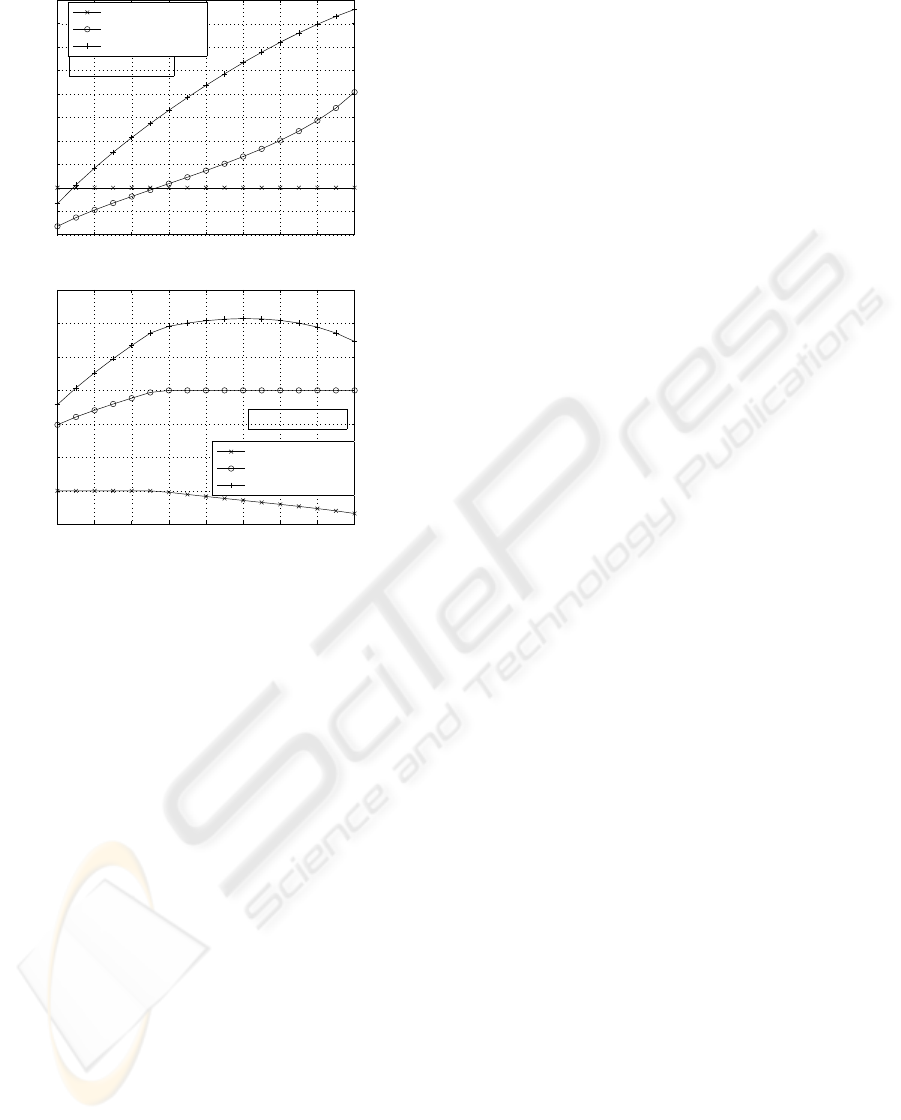
optimization model, Fig.8 illustrates charging rate of

GPRS and Wi-Fi networks as well as the revenue gen-

erated from those charges. r

and r

are subject to

constraints [1,4] and [3,10] according to the pricing

information from commercial GPRS operators and

Wi-Fi aggregators. We can see that, when average

session volume equals 2 MB, the optimal r

is at 4

dollars per MB for any target user demand D. The

maximum revenue and user demand of the integrated

network are, however, driven by r

as they increase

along with r

. For the larger session volume,i.e.,

5 MB, at D equals 0.5, r

would reach the maxi-

mum market price (10 dollars per connection). The

optimization model suggests that the GPRS operator

should reduce the GPRS charge r

in order to meet

certain user demand and maximum revenue. Hence,

based on our assumption and the optimization model,

A PRICING MODEL OF GPRS NETWORKS WITH WI-FI INTEGRATION FOR “HEAVY” DATA USERS

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

3.5

4.5

5.5

6.5

7.5

User Demand (D)

Price and Revenue ($)

GPRS charging rate (r

)

Wi−fi Connection fee (r

)

Revenue (R

int

)

Session Volume = 2MB

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

User Demand (D)

Price and Revenue ($)

GPRS charging rate (r

)

Wi−Fi Connection fee (r

)

Revenue (R

int

)

Session Volume=5MB

Figure 8: Price sets generated from optimization model and

their corresponding revenue.

we can create price sets for both GPRS and Wi-Fi

networks which allow us to migrate trafﬁc demand

between these two networks and yield maximum rev-

enue.

5 CONCLUSION

In this paper we propose a simple but effective pricing

model of GPRS networks integrated with Wi-Fi. We

propose the use of demand functions to describe the

response of users based on the prices charged in each

networks. By integrating two technologies together,

operators can attract new customers with value added

services provided by Wi-Fi networks, thereby, reduc-

ing the churn. Furthermore, the GSM/GPRS cellular

operators can delay their 3G deployments as the inte-

gration could offer 3G-like services. The integration

is not only beneﬁcial to the cellular operator but also

to third party hotspots, because it increases revenue

by increasing trafﬁc load at their hotspot networks.

Users who are not willing to pay high GPRS prices,

will eventually start utilizing the Wi-Fi network, tak-

ing advantage of the price difference. Thus, integra-

tion provides proﬁtable business strategy for both the

cellular operators and the new Wi-Fi startup compa-

nies.

To extend our study, we are investigating the distri-

bution of GPRS session volume and the estimation of

trafﬁc load migrated from GPRS to Wi-Fi.

REFERENCES

A. K. Salkintzis, C. Fors, and R. Pazhyannur (2002).

WLAN-GPRS integration for next-generation mobile

data networks. In IEEE Wireless Communications.

vol. 9, Issue. 5, October 2002, pp.112-124.

K. Ahmavaara, H. Haverinen, and R. Pichna (2003). Inter-

working architecture between 3GPP and WLAN sys-

tems. In IEEE Communications Magazine. vol.41, Is-

sue.11, November 2003, pp.74-81.

L. Anania and R. J. Solomon (1997). Flat - the mininalist

price. In L.W. McKnight and J.P. Bailey, editors, In-

ternet Economics. Cambridge, Massachusettes, 1997,

MIT Press.,pp. 91-118

J. K. MacKie-Mason and H.R. Varian (1995). Congestible

Network Resources. In IEEE Journal on Selected Ar-

eas in Communications. vol.13, issue. 7, Sep 1995,

pp.1141-1149.

M. Falkner (2000). A user’s perspective on Connection Ad-

mission Control: Integrating Trafﬁc Shaping, Effec-

tive Bandwidths and Pricing. Doctoral thesis at Car-

leton University, Ottawa, Ontario, May 12,2000.

A.M. Odlyzko (1999). Paris Metro Pricing: The minimalist

differentiatedservices solution. In Proc. Seventh IEEE

International Workshop on Quality of Service. 1999,

pp.159-161.

C. Courcoubetis, F. P. Kelly, V. A. Siris and R. Weber

(2000). A study of simple usage-based charging

schemes for broadband networks. In Telecommuni-

cations Systems. 2000, pp.323-343.

A. Doufexi, E. Tameh, A. Nix, S. Armour, A. Molina

(2003). Hotspot wireless LANs to enhance the per-

formance of 3G and beyond cellular networks. In

IEEE Communications Magazine. vol.41, Issue 7,

July 2003, pp. 58-65.

S. Oliver, and P. Poiraud (2002). Public WLAN for mobile

operators. White paper, Atcatel, 2002.

J. Hou, J. Yang, and S. Papavassiliou (2001). Integration

of Pricing with Call Admission Control for Wireless

Networks. In Proc. Vehicular Technology Conference.

vol. 3, 2001, pp.1344 -1348.

P. C. Fishburn and A. M. Oldyzko (2000). Dynamic behav-

ior of differential pricing and quality of service op-

tions for the internet. In Decision Support Systems. 28

(2000), pp. 123-136.

J. Kilpi (2003). A portrait of a GPRS/GSM session. In 18th

International Teletrafﬁc Congress. Germany, Septem-

ber 2003.

Boingo, http://www.boingo.com

ICETE 2005 - WIRELESS COMMUNICATION SYSTEMS AND NETWORKS