EFFICIENT CALL ADMISSION CONTROL FOR 3G
NETWORKS
Chernoff-Bound based CAC
Albert Mráz, Mihály Katona
Mobile Communication Laboratory, Budapest Univ. of Technology and Economics, Magyar Tudósok krt. 2., 1117 Hungary
Dr. Sándor Imre
Mobile Communication Laboratory, Budapest Univ. of Technology and Economics, Magyar Tudósok krt. 2., 1117 Hungary
Keywords: Effective bandwidth technique, Chernoff-bound, Dynamic CAC.
Abstract: In the recent years the mobile telecommunication networks have gone through on a big development. The
services of the systems have been extended very quickly, such as the number of the subscribers. The various
multimedia and Internet systems have become quickly the part of our life. This phenomenon takes effect on
mobile communication, too. The third-generation mobile networks could be the solution, which eliminate
the defects of current systems and apply good solutions concerning both access and transport system. These
3G systems are able to meet the growing user demands and the mobile Internet requirements. Our goal is to
use the scarce resources as efficiently as possible. We implemented a new, more efficient and faster call
admission control than former methods. Our algorithm is able to be adapted directly for 3G mobile
networks.
1 INTRODUCTION
The 3G mobile communication networks operate
according to Code Division Multiple Access
method. There is a major change between the
methodology of the first and second generations
mobile networks (FDMA and TDMA) in call
admission control (CAC) policy. FDMA and TDMA
networks have a hard limit for the number of
subscribers operating in the network simultaneously.
In the 3G CDMA systems there are no maximum
limits for the number of simultaneously
communicating users, because this number is
determined by the user interference. Our task is to
answer the question, whether the prescribed service
quality (QoS) is defensible when a new call request
is coming in. The main purpose is to create a call
admission control method, which can adapt
dynamically to an ever-changing mobile
environment.
We compared our method to an algorithm (Evans
and Everitt, 1999), which uses pre-calculated
effective bandwidth values which on the first hand
requires computationally complex (time-consuming)
recalculation every time when the system parameters
have been changed, and on the other hand these
values are optimized for an average network
scenario and not for a given one. Hence these values
don’t provide optimal call admission control.
We introduce a new, fast and efficient algorithm
which is able to calculate the optimal effective
capacity values for a given network scenario. Our
solution is based on the real-time estimation of the
well-known Chernoff bound (Imre, 1999).
This paper is organized as follows: In Section 2
we give an interpretation of call admission control.
In the next section we describe the ON/OFF source
model that we use. The introduction of the effective
bandwidth technique as it was written in (Evans and
Everitt, 1999) is the subject of Section 4. In section
5 we introduce the theoretical framework of CAC. In
section 6 we make a transformation of CAC method
so that it can be used in CDMA environment.
Section 7 we present the simulation results we got
and comparison between our method and the one
given in (Evans and Everitt, 1999).
66
Mráz A., Katona M. and Imre S. (2005).
EFFICIENT CALL ADMISSION CONTROL FOR 3G NETWORKS - Chernoff-Bound based CAC.
In Proceedings of the Second International Conference on e-Business and Telecommunication Networks, pages 67-73
DOI: 10.5220/0001415500670073
Copyright
c
 SciTePress

2 GEOMETRIC
INTERPRETATION OF CAC
In order to give a generalized description of call
admission procedures we introduce the following
scenario. Each mobile source is grouped into traffic
classes. Every sources in a given traffic class have
the same traffic descriptors (e.g. maximum
transmission rate, average traffic rate, etc.) and
number of active sources in the ith class is denoted
by Ni. Therefore the state of the system in every
moment can be described by a state vector
N = (N
1
, N
2
,…, N
J
), (1)
where J refers to the number of traffic classes.
Now the call admission procedure means that we
should decide whether a new call can be accepted
without violating the QoS parameter guaranteed for
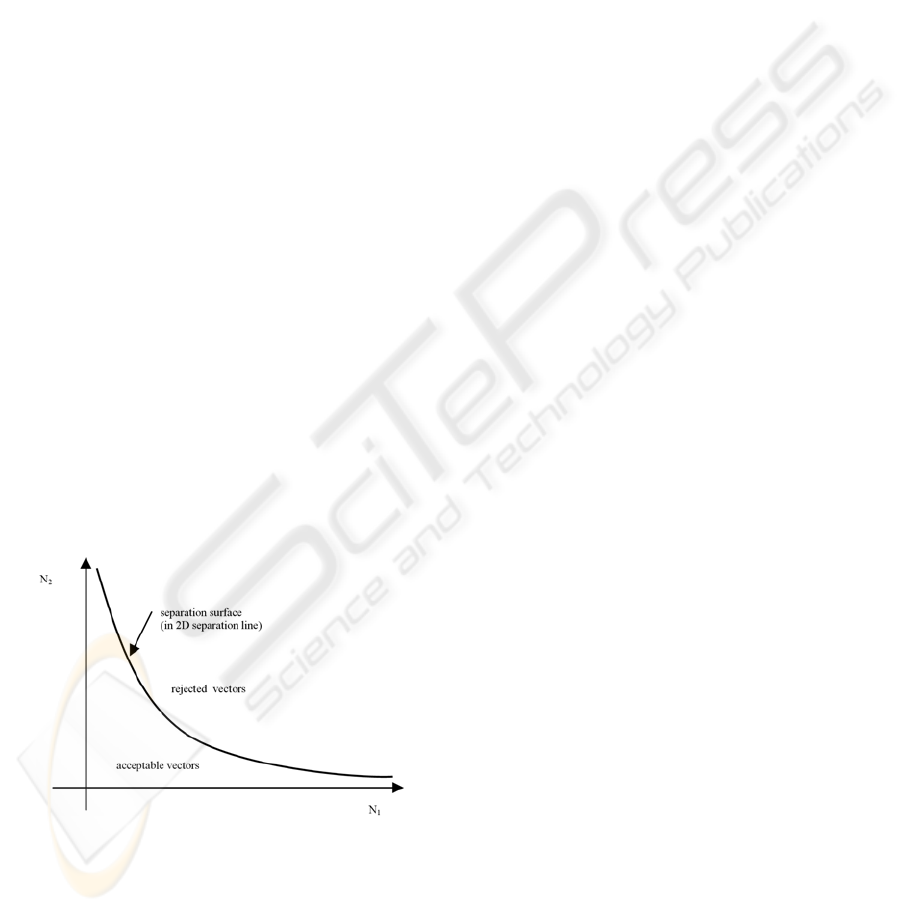
other users or not. All state vectors can be divided
into two sets (geometric interpretation at Figure 1.).
Vectors that can be accepted by the network
management without violating the traffic contracts
belong to the first (or acceptable) set and states that
must be rejected to the second (or rejected) set
V
ACCEPT
:={N:
()
γ
<> CXP
} (2)
V
REJECT
:={N:
()
γ
≥> CXP
}, (3)
where X refers to the overall traffic of the users and
C is the system capacity and
γ denotes the QoS
parameter. Therefore the task of CAC can be
regarded as a space separation problem that is to say
how to determine the surface, that separates the two
regions and how to decide whether the new traffic
state of the link is on the acceptable or rejected side
of the separation surface.
Figure 1: Geometric interpretation of CAC
Unfortunately the CAC decision cannot be
carried out directly on the basis of the theoretical
surface. First the calculation of exact separation
surface proves to be a hard task because of the high
computing complexity. Secondly the size of the
space of the theoretical surface needs enormous
large storage capacity.
3 APPLICATION OF ON/OFF
SOURCE MODEL
In order to give a simple but widespread and close
approximation of the subscribers’ data traffic we use
the ON/OFF model.
According to this model the traffic of a subscriber
is estimated by a source which has two states, either
it transmits with peak bit rate or it remains in
silence, therefore the bit rate distribution of the
ON/OFF source contains values different from zero
only at nil and at peak bit rate on the axis of bit rate.
An ON/OFF source which describes the jth
subscriber can be characterized with a peak rate (Rj
or hj) and a probability (Φj) being ON. The Φj is
known as the voice activity factor (VAFj). Then the
mean bit rate can be calculated as
jjj
VAFhm
⋅
=
(4)
4 APPLICATION OF STATIC
EFFECTIVE BANDWIDTHS
The users are grouped into traffic classes and an
effective bandwidth (Kelly, 1991), (Elwalid, 1993)
value is assigned to each type of user (class) which
is somewhere between the mean rate and the peak
rate of the variable bit rate (VBR) user. Then the
actual value of the required system bandwidth is
estimated by means of the effective bandwidth
values and the number of the users in different
classes. The effective bandwidth values are
depending on the QoS parameters and on the
stochastic behaviour of the users’ traffic as well.
Now we describe the method of the effective
bandwidth so that later we can compare it with our
method. Let
J
Z
+
denote the set of J-tuples (J refers to
the number of classes) of non-negative integers and
consider the problem of finding the set of points
(
)
J
J
ZNNN
+
∈,...,,
21
satisfying
γ −
==
≤
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
>
∑∑
eCXP
J
j
N
i
ji
j
11
(5)
where X
ji
, i = 1,…, N
j
, j = 1,…, J models the
independent random amount of resource required by
call i of class j, C is the total amount of resource
available,
γ is the quality of service requirement, and
the N
j, j = 1,..., J are the number users of each class.
Inequality (5) represents the well-known tail
distribution estimation problem, which requires the
EFFICIENT CALL ADMISSION CONTROL FOR 3G NETWORKS-Chernoff-Bound based CAC
67

convolution of large number of random variables.
Because calculation of convolution is rather time
consuming task so the theoretical amount of
resource is approximated by application of effective
bandwidth without significant calculation power.
Let replace (5) by the following inequality
CN
J
j
jj
≤
∑
=1
κ
, (6)
where κ
j
refers to the effective bandwidth of the jth
class. We remark that the effective bandwidth based
solution approximates the theoretical separation
hypersurface with a hyperplane, which is not the
optimal solution but it realizes fast call admission
decisions.
A promising way to calculate the effective
bandwidth values (κ
j
), is the Chernoff bound, which
upper bounds the tail distribution. This means that
we shall calculate the logarithmic moment
generating function (LMGF) M
j
(s), of a class j
random variable, which transforms (5) to:
γ −
=
≤
⎥
⎦
⎤
⎢
⎣
⎡
−
∑
esCsMN
J
j
jj
s
1
)(inf
. (7)
The main advantage of the Chernoff bound (Kelly,
1991), (Bucklew, 1990) lies in the optimization
parameter s, which allows to find the tightest upper
bound for the tail.
After that a network state
()
J
J
ZNNN
+
∈,...,,
21
is admissible if it satisfies (7).
In case of effective bandwidth concept a tangent
hyperplane at the point
),...,,(
**
2
*
1 J
NNN
on the
theoretical separation hypersurface can be used to
approximate the theoretical hypersurface. To
determine the coordinates of this point one needs to
calculate the optimal value of the s parameter
*
1
*
)(infarg ssCsMN
J
j
jj
s
=
⎥
⎦
⎤
⎢
⎣
⎡
−
∑
=
. (8)
Unfortunately to find the optimum value for
parameter s according to (8) requires a large amount
of computation as well, because it assumes the
knowledge of separation surface; but it have to be
determined once before starting the service and
during the operation we shall only decide whether
the inequality (6) remains valid or not.
5 DYNAMIC CHERNOFF BOUND
BASED CAC
In order to provide real-time optimization which
results faster and more effective CAC decision we
developed a Chernoff bound based call admission
control algorithm.
The following lemma has already proved in
(Billingsley, 1986):
Let X be a random variable which has expectancy
value. For all C > 0 and s > 0 real number it is true
the following inequality holds:
(
)
(
)
Cse
Xs
eCXP
⋅−
⋅
<>
)(Eln
. (9)
If we can guarantee:
(
)
γ −⋅−
<
⋅
ee
Cse
Xs
)(Eln
, (10)
then the call can be admissible according to (9).
γ
refers to the QoS parameter. We take the natural
logarithm of both sides of (10) and restructure it:
(
)
0)(Eln <+⋅−
⋅
γ Cse
Xs
(11)
On the left hand side we have the
Xs
e
⋅
random
variable logarithmic moment generating function, in
case of number of J independent source in further
simplicity it will be shown as follow (Imre, 1999)
(
)
)(Eln:)(
J
J
Xs
X
es
⋅
=Ψ
, (12)
where X is indicating the distribution function of the
total traffic for J piece of source.
For the use of the inequality (11) we have to
solve the following problems.
• We have to determine
)(s
J
X
Ψ
for the
overall traffic.
• A new method has to be find, which can
determine the optimal value
opt
J
s
of
parameter s.
5.1 Determination of the total traffic
logarithmic moment generating
function
This is known for independent random variables:
,)(E)(E
J
1
∏
=
⋅
⋅
=
j
Xs
Xs
j
J
ee
(13)
so inequality (9) can be transformed into the
following form:
()
()
,)(Eln)(Eln)(Eln)(
1
1
∑
∏
=
⋅
=
⋅
⋅
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
==Ψ
J
j
Xs
J
j
Xs
Xs
X
jj
J
J
eees
(14)
which is equal with use of:
∑
=
Ψ=Ψ
J
j
XX
ss
jJ
1
)()(
. (15)
This is a very important result, as the convolution is
converted to a sum which is a more simple
operation.
ICETE 2005 - WIRELESS COMMUNICATION SYSTEMS AND NETWORKS
68

We model the users as ON/OFF sources with
parameters (m
j
, h
j
); hence the logarithmic moment
generating function is given:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅+−==Ψ
⋅
j
OFFON
j
hs
j
j
j
j
X
j
e
h
m
h
m
sKs 1ln)(:)(
/
(16)
After the comparison of (16) with the result of (11)
and (15), the call admission control in case of
ON/OFF sources, requires the evaluation of the
following inequality:
.01ln:)(
1
<+⋅−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅+−=
∑
=
⋅
γ Cse
h
m
h
m
NsK
J
j
hs
j
j
j
j
jJ
j
(17)
5.2 Determination of the optimal
value for the Chernoff-
parameter in case of ON/OFF
sources
Gallager shown (Gallager, 1968), that the inequality
(6)
0>∃s
, where the
()
γ −⋅−
−
⋅
ee
Cse
J
Xs
)(Eln
expression is minimal and the s value is possible to
determine with derivation if
)(Emax
JJ
XCX >>
.
From this result for the inequality (11)
opt
J
s∃ if
∑∑
==
>>
J
j
j
J
j
j
mCh
11
.
To determine
opt
J
s
we have to make the derivation of
expression (13)
0
1
)('
1
=−
⋅+−
⋅
=
∑
=
⋅
⋅
C
e
h
m
h
m
em
sK
J
j
hs
j
j
j
j
hs
j
J
j
j
. (18)
Unfortunately
opt
J
s
cannot be calculated explicitly
from (18), and Gallager’s lemma also does not give
any kind of solution to determine
opt
J
s
. But it can be
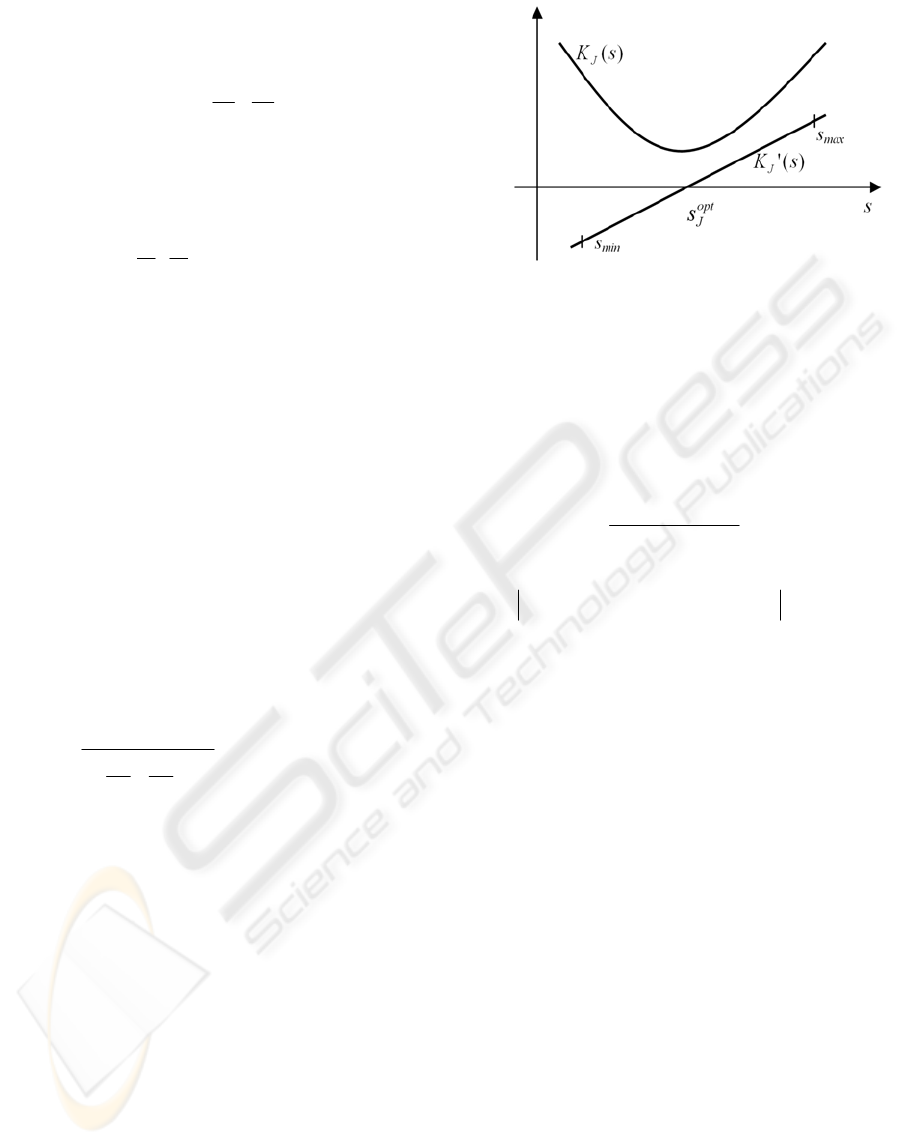
seen that
)(' sK
J
is a strictly monotonous increasing
function of s > 0. So
opt
J
s
, which can be found at the
point of intersections
)(' sK
J
. And axis s, can be
determined by the means of logarithmic search
algorithm.
Figure 2: Determination of
opt
J
s
.
Operation of the logarithmic search algorithm:
we have to define the
)]0(),0([ == iSiS
upper
J
lower
J
interval which contains the
opt
J
s , where i is the
number of iteration steps.
)]0(),0([ == iSiS
upper
J
lower
J
interval has to be
mediated:
2
)()(
)()(
iSiS
iSis
upper
J
lower
J
lower
J
median
J
−
+=
we have to calculate
))(( isK
median
JJ
))1(())(( −−=∆ isKisK
median
JJ
median
JJ
if
d
≤
∆
then )(is
median
J
approximated
opt
J
s
satisfactorily and the algorithm stops running. d
refers to the threshold of stop
if
d>
∆
then we have to calculate the value of
))((' issK
median
JJ
=
if
))((' issK
median
JJ
=
>0, then
opt
J
s
is under the
)(is
median
J
because of
)(' sK
being strictly
monotonous; we have to choose
)1( +iS
upper
J
=
)(is
median
J
,
)()1( iSiS
lower
J
lower
J
=+
if
))((' issK
median
JJ
=
<0, then
opt
J
s is above
)(is
median
J
, we have to choose
)1( +iS
lower
J
=
)(is
median
J
,
)1( +iS
upper
J
=
)(iS
upper
J
we have to return to the second step.
The logarithmic search gives a fast algorithm with a
small number of iterations, which can be run before
every new CAC decision (Imre, 1999).
EFFICIENT CALL ADMISSION CONTROL FOR 3G NETWORKS-Chernoff-Bound based CAC
69

6 CAC MODEL FOR CDMA
NETWORKS
In this section we show how to model CDMA
cellular networks from CAC point of view.
The individual sources are grouped into traffic
classes. Each user belonging to the same class has
the same mean bit rate (m) and peak bit rate (h). The
users are described with its required signal to
interference density ratio (SIDR) as well
0
I
E
b
= α
, (19)
where E
b
refers to the bit energy and I
o
is the power-
density of interference. Furthermore the sensitivity
of the mobile receivers can be characterized with
0
I
E
R
b
kk
⋅=Γ
, (20)
which has Hz dimension and R
k
refers to the peak bit
rate of the kth class.
In CDMA systems the number of communicating
subscribers in a moment is limited by the current
SIDR.
Consider the network from the perspective of a
given cell. The mobiles in this examined cell
generate the interference to the receiver and the
mobiles positioned in the neighbouring cells also
generate it. We are taking account of three different
types of cells depending on the distance from the
Base Station. The first type of cell is the originated
cell. The second type of cell is the neighbour cell of
the originated cell and the third type of cell is the
second neighbour of the originated cell (Evans and
Everitt, 1999). The major part of the interference is
generated at cell type 1, 2 and 3, the effect of that
further ones are negligible.
6.1 Chernoff parameter
transformation
The Chernoff bound calculation requires two
parameters called m and h. In order to determine
these parameters we use two-ways propagation
model [9] for simplicity reason, as it is easy to count
and implement. From (Evans and Everitt, 1999) we
got the following parameters:
Type 1 (own cell):
2
2
21
3
2
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⋅Γ=
c
kj
r
ll
h
(21)
Type 2 (first neighbour cells):
2
2
21
)3(
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⋅Γ=
c
kj
r
ll
h
(22)
Type 3 (second neighbour cell):
2
2
21
2
)323(
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⋅
⋅Γ=
cc
kj
rr
ll
h
(23)
Furthermore for each types of cells
kjj
VAFhm
⋅
=
. (24)
We create virtual new classes, which have to be
taken account by the call admission algorithm during
call admission procedure
7 SIMULATION RESULTS
We implemented a simulator program (in C++)
implementing the two call admission control
algorithms.
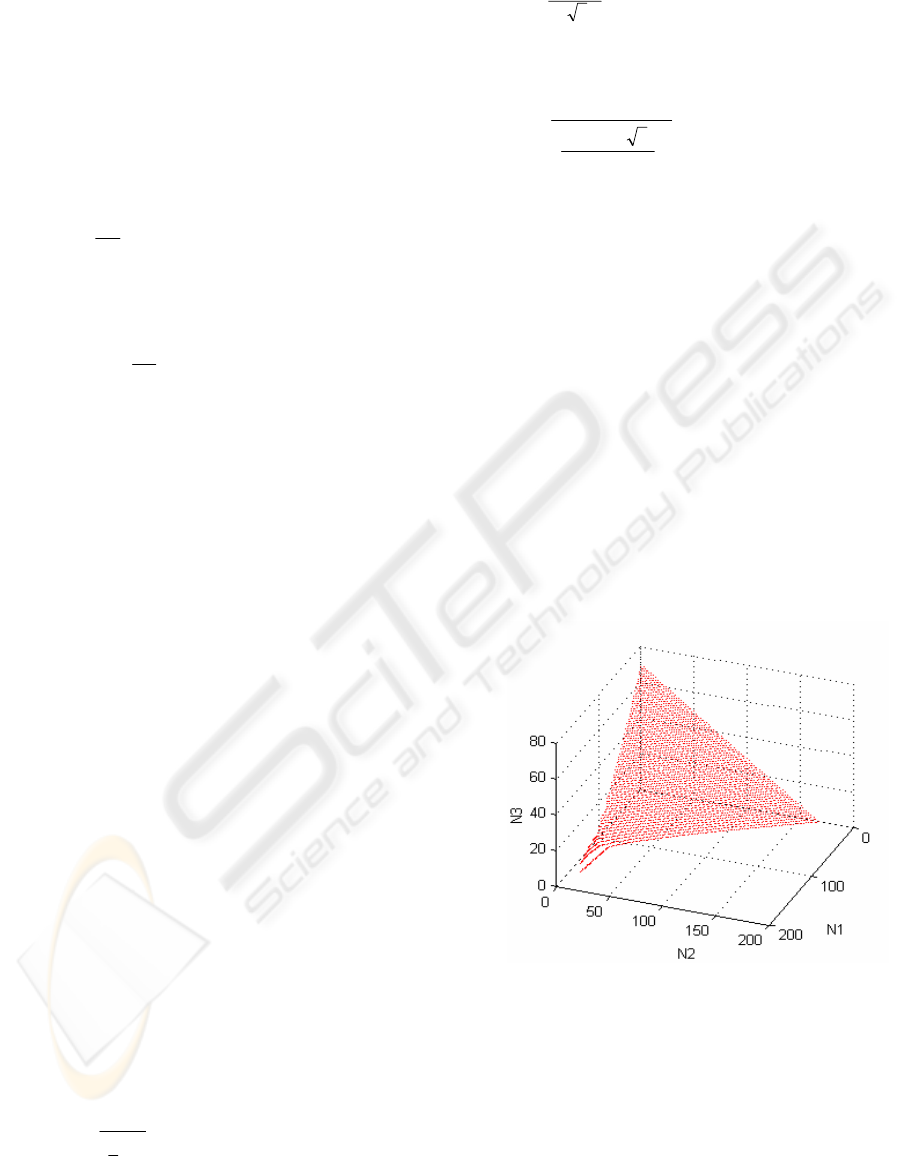
At first we show the separation surface (in 3D) of
a real network.
The network parameters are:
C=2.5 MHz; γ=2;
m
1
=20 kbps; m
2=
10 kbps; m
3=
20 kbps
h
1
=50 kbps; h
2=
100 kbps; h
2=
200 kbps
Figure 3: Separation surface in 3D.
By the second simulation (Figure 4) we watch the
number of acceptable vectors by growing subscriber
number in the neighbour cells:
The network parameters:
C=2.5 Mhz; γ=2;
h
1
= 50 kbps; h
2
= 100 kbps;
m
1
= 20 kbps; m
2
= 10 kbps;
E
b
/I
0
=7 dB; l
1
=30 m; l
2
=1 m; r
c
=50 m.
Number of calls: 1000
ICETE 2005 - WIRELESS COMMUNICATION SYSTEMS AND NETWORKS
70

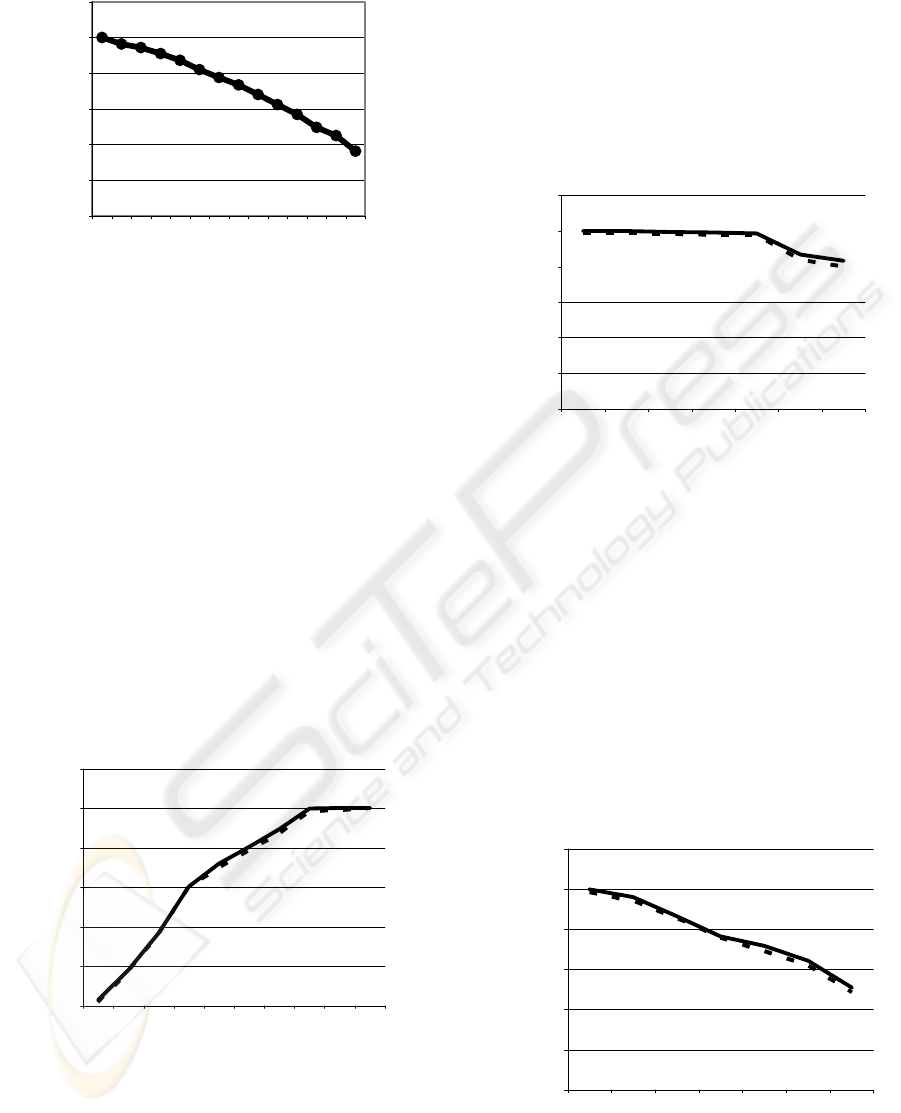
0
200
400
600
800
1000
1200
100 110 120 130 140 150 160 170 180 190 200 210 220 230
Number of interference sources
Number of acceptable calls
Figure 4: Acceptable calls by changing the number of
interference sources.
We can see that as the number of subscribers is
growing in the neighbour cells, the interference
increases, that’s why the number of the acceptable
calls falls off.
We illustrate the differences between the two call
admission control methods at the next three figures.
Continuous line denotes the results of the dynamic
call admission control. Dotted line signs the
outcome of the effective bandwidth based method.
At the first case we can observe the formation of the
acceptable calls in function of the system capacity
(C).
System parameters are:
λ
1
= 0.1; µ
1
= 0.005; λ
2
= 0.2; µ
2
= 0.002;
h
1
= 50 kbps; h
2
= 100 kbps;
m
1
= 20 kbps; m
2
= 10 kbps; e
-γ
= 10
-2
0,0000
200,0000
400,0000
600,0000
800,0000
1000,0000
1200,0000
0,2
00
0
0,6
00
0
1,0
00
0
1,4
00
0
1,6
00
0
1,8
00
0
2,0
00
0
2,5
00
0
2,6
00
0
3,0
00
0
C [MHz]
Acceptable calls
Figure 5: Number of acceptable calls by changing of C.
It’s visible, that the results of the dynamic call
admission control method are always higher than the
values of the other method as C grows.
In the second case we changed the peak bit rate of
the users in the first traffic class, and observed the
formation of the number of acceptable call requests.
System parameters:
λ
1
= 0.1; µ
1
= 0.005; λ
2
= 0.2; µ
2
= 0.002;
C=2,5 Mhz
h
1
= changing; h
2
= 100 kbps; m
1
= 20 kbps; m
2
= 10
kbps;
e
-γ
= 10
-2
0,0000
200,0000
400,0000
600,0000
800,0000
1000,0000
1200,0000
0,0500 0,0600 0,0800 0,1000 0,1500 0,5000 0,6000
h1
Number of acceptable calls
Figure 6: The number of acceptable calls by the changing
of h
1.
We can observe like in the previous case, the
dynamic method provides better and better results as
the traffic is more and more bursty.
By the last comparison simulation we changed the
time length between the call requests, which
decreases as λ
2
grows.
System parameters are:
λ
1
= 0.1; µ
1
= 0.005; λ
2
= changing; µ
2
= 0.002;
C=2,5 Mhz;
h
1
= 50 kbps; h
2
= 100 kbps; m
1
= 20 kbps; m
2
= 10
kbps;
e
-γ
= 10
-2
.
0,0000
200,0000
400,0000
600,0000
800,0000
1000,0000
1200,0000
0.2 0.25 0.3 0.35 0.4 0.45 0.6
lambda2
Number of acceptable calls
Figure 7: Number of acceptable calls by the changing of
λ
2.
EFFICIENT CALL ADMISSION CONTROL FOR 3G NETWORKS-Chernoff-Bound based CAC
71

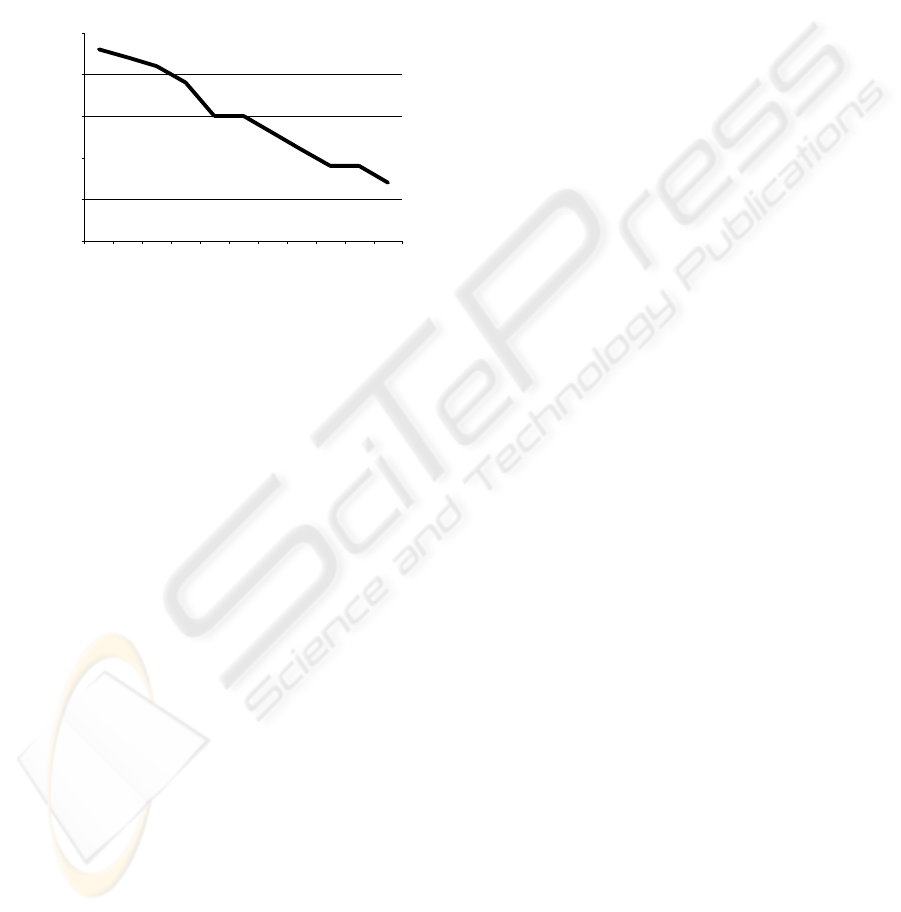
The increase of
λ
2
means, when the average call
time lengths (in the second traffic class) are
decreasing, we can observe that call requests arrive
more often, thus the number of the acceptable call
requests is smaller. The dynamic call admission
control gives more acceptable calls in this case, too.
By the running of the simulator we illustrated the
number of iteration steps, which are necessary to
calculate the value of s
opt
. The stop threshold (d) is
changing.
0,0000
5,0000
10,0000
15,0000
20,0000
25,0000
1,0
0
E-
12
1,0
0
E-11
1,0
0
E
-10
1,0
0
E-09
1,0
0
E
-08
1,0
0
E-07
1,0
0
E
-06
1,0
0
E-0
5
1
,00
E
-04
1,0
0
E-
03
1,0
0
E-02
d
Number of iteration steps
Figure 8: Number of iteration steps by different accuracy
demands.
It’s shown, that the value of d = 10
-3
– 10
-4
provides a very precise approximation to the s
opt
, in
this case the number of iteration steps is only 9, what
denotes we come relatively fast to the optimal value
of s
opt
.
8 CONCLUSION
In mobile communication systems we need more
efficient CAC method than in the former systems,
because by radio systems we can only use a very
straitened and expensive resource kit (the frequency
band). In the wire line networks this problem isn’t
important, because the capacity of the system can be
extended by switching extra links. In mobile systems
we can’t do it.
The parameters (interference, delay etc.) of the
radio channel are always changing. The effective
bandwidth based algorithm (Evans and Everitt,
1999) dismisses these effects, so its efficiency isn’t
satisfying. We can’t use the frequency band
economically with this method. In addition the CAC
method described in (Evans and Everitt, 1999) can’t
be run real time because of its large computation
demand.
We made a new CAC method, which can adopt
dynamic to the always changing network
parameters. We had to find a faster way for
calculating of the Chernoff bound. The logarithmic
search algorithm gives a fast operation to the CAC
method, so it becomes able to be run every time
when the system parameters are changing. So we
can call our new CAC method dynamic. In addition
the simulation results show that the dynamic call
admission control method gives every time more
acceptable calls than the effective bandwidth based
method.
The dynamic CAC method has two advantages. It
can adapt to the mobile environment, and accepts
more call requests than the former methods. By the
acceptance of more calls we use the very expensive
radio resources more economical.
In the future can be developed the dynamic CAC
method with more complex network and radio
channel models, because by employing of more
realistic models can we get acceptable calls, growing
the efficiency of the CAC method. Our plans are to
implement Rayleigh- or Rice-fading, or using other
traffic models than ON/OFF sources.
REFERENCES
J.S Evans and D Everitt, Effective bandwidth-based
admission control for multi-service CDMA cellular
networks, IEEE Transactions on vehicular technology
48 (1) (1999) 36-46
dr. Sandor Imre, Call Admission Control Methods in ATM
network, 1999. pp. 100
S. Imre, K. Hankó, P. Petrás, R. Tancsics, "Optimized
Effective Bandwidth Based Admission Control for
Multi-Service CDMA Cellular Networks", 10th
SoftCOM2002, October 08-11, 2002, Split, Dubrovnik
(Croatia), Ancona, Venice (Italy), Published at FESB-
Split, ISBN 953-6114-52-6, pp. 299-304
F. P. Kelly, Effective bandwidth at multi-class queues,
Queuing Systems, vol. 9, pp. 968-981, Sept. 1991
A. I. Elwalid and D. Mitra, Effective bandwidth of general
Markovian traffic sources and admission control of
high speed networks, IEEE/ACM Trans. Netw., vol. 1,
pp 329-343, June 1993.
J. A. Bucklew, Large Deviations Techniques in Decision,
Simulation and Estimation, New York: Wiley 1990.
P. Billingsley, Probability and Measure, 2
nd
ed. New York,
Wiley, 1986.
Gallager, R. G.: Information Theory and Reliable
Communication, John Wiley and Sons, 1968.
R. Kohno, R. Median, and L. B. Milstein, “Spread
spectrum access methods for wireless
communications”, IEEE Commun. Mag, Jan 1995.
ICETE 2005 - WIRELESS COMMUNICATION SYSTEMS AND NETWORKS
72