PERFORMANCE EVALUATION OF 3G CORE NETWORK
NODES
Andrey Krendzel, Jarmo Harju
Tampere University of Technology (TUT), Institute of Communications Engineering, Tampere, Finland
Sergey Lopatin
St.-Petersburg Research and Development Institute of Telecommunications (LONIIS), St.-Petersburg, Russia
Keywords: the Third Generation wireless systems, Universal Mobile Telecommunication System, Internet Protocol
Multimedia Core Network Subsystem, Fractional Brownian Motion, self-similarity.
Abstract: Wireless network planning is a very complex process, the result of which influences on the success of
network operators. A poorly planned network cannot achieve the required Quality of Service. It also
involves extra costs and fewer benefits for its network operator. Actually, wireless network planning deals
with a large number of different aspects. In this paper Core Network (CN) planning aspects for the third
generation (3G) wireless systems are discussed. The problem of performance evaluation of 3G CN nodes
for Internet Protocol Multimedia Core Network Subsystem (IM CN subsystem) is considered in details
taking into account self-similarity caused by the high variability of burstiness of multiservice traffic in 3G
wireless networks. The method for the problem solution is based on the use of FBM/D/1/W queueing
system (FBM – Fractional Brownian Motion).
1 INTRODUCTION
There has been an evolution in wireless
communications almost every ten years. The first
generation (1G) in 1980s and the second generation
(2G) mobile systems in 1990s have been oriented
mainly for providing circuit-switched (CS) services
to users. The 2G subscribers have used the rate for
data transfer up to 14 kb/s as a maximum. In 1996,
European Telecommunications Standards Institute
(ETSI) decided to enhance 2G GSM standard in
annual Phase 2+ releases that incorporate the third
generation (3G) features such as General Packet
Radio Service (GPRS) and Enhanced Data Rates for
GSM Evolution (EDGE). The data rates for users of
the systems are limited to less than several hundreds
of kb/s.
Universal Mobile Telecommunications System
(UMTS) as the 3G mobile system will be introduced
during first decade of new century. It is specified by
ETSI and the world-wide 3G Partnership Project
(3GPP) within the framework defined by the
International Telecommunication Union (ITU) and
known as International Mobile Telecommunications
- 2000 (IMT-2000). The 3G systems can support 2
Mb/s for indoor environments and at least 144 kb/s
for vehicular environments.
ETSI and 3GPP are introducing UMTS in
phases and annual releases. UMTS Rel’3
(sometimes called as Rel’99) is a 3G GSM successor
standard using the GSM Phase 2+ enhanced core
network (CN). The most important evolutionary step
toward UMTS is to introduce a packet switched core
network (PS CN) domain. The main function of the
PS CN domain is to support all services (GPRS,
WAP, etc.) provided to both GSM subscribers and
UMTS users (Kaaranen H. , et. al 2001).
The following phases after Rel’3 specify how
voice and multimedia can be supported by IP
technology. It is characterized by creating of the
Internet Protocol (IP) Multimedia Core Network
Subsystem (IM-subsystem), which comprises all PS
CN domain elements for providing
telecommunication services within UMTS Rel’4,5,6.
The IM-subsystem contains a uniform way to
maintain Voice over IP (VoIP) calls and offers a
platform to multimedia services. The examples of
IM services are voice telephony, real-time
interactive games, videotelephony, instant
97
Krendzel A., Harju J. and Lopatin S. (2005).
PERFORMANCE EVALUATION OF 3G CORE NETWORK NODES.
In Proceedings of the Second International Conference on e-Business and Telecommunication Networks, pages 98-104
DOI: 10.5220/0001415600980104
Copyright
c
 SciTePress

messaging, emergency calls, multimedia conferencing (Bale M.C. , 2001). In the UMTS
Rel’5,6 all traffic coming from Radio Access
Network (RAN) to the CN is supposed to be all IP
based (Kaaranen H. , et. al 2001).
The next step of wireless communications
evolution is the fourth generation (4G) of mobile
communication systems (the systems beyond IMT-
2000). Now it is difficult to predict when the 3G
evolution ends and the 4G really starts (Kaaranen
H. , et. al 2001). The 4G systems should offer
significantly higher bit rate than 2 Mb/s, have high
capacity with a low bit cost and be able to support
all type of telecommunication services from the
viewpoint of multimedia communications
(Y.Yamao et. al, 2000). It is supposed that on the
CN side of the 4G systems the main purpose is to
minimize changes and utilize the 3G CN elements
and the 3G CN functionality as much as possible
(Kaaranen H. , et. al 2001). The CN development is
summarized in the Table I.
There are some important features of the global
evolution process in wireless communications.
The 3G wireless systems should be designed to
support for a high-speed transfer of a large amount
of multimedia information between users. One of
the main properties of the data traffic in the 3G
systems is a large diversity depending on the profile
of services provided to 3G users. It is expected that
the traffic in the 3G systems will expand
considerably (The UMTS 3G Market Forecasts,
2002).
Table 1: Core Network development
GENERATIONS OF
WIRELESS
SYSTEMS
CORE NETWORK
DOMAINS
2G CS CN
2G phase 2 + CS CN and PS CN
3G (UMTS Rel’3) CS CN and PS CN
(enhanced 2G phase 2 +
CN)
3G (UMTS Rel’ 4) CS CN, PS CN, IM CN
3G (UMTS Rel’ 5,6) IM CN
4G IM CN
(enhanced 3G CN)
The growing data/multimedia traffic leads to
increasing the total load on network subsystem
elements. Moreover, traffic patterns generated by
3G services may be quite different from traditional
Poisson models used for circuit switched voice
traffic. When modeling packet-switched
multiservice networks it is necessary to take into
account the notion of self-similarity (M. Jiang et al.
2001), (V. Paxson, S.Floyd, 1994). Due to the high
variability of burstiness of the traffic, the use of the
classical teletraffic theory for a performance
evaluation of PS CN domain elements may give
essential faults; in particular, the network
parameters can be underestimated. Such faults are
unacceptable when IM-subsystem planning as well,
therefore, principles of the teletraffic theory cannot
be applied in this case.
Due to above reasons, the following 3G
network planning problems occur:
• the prediction problem of a demand for 3G
services;
• the estimation problem of 3G data traffic
parameters;
• the problem of the performance evaluation
of IM-subsystem nodes taking into account the
self-similar nature of the multiservice traffic.
It is seen from the Table 1 that the CN evolution
is quite temperate. From the viewpoint of functional
capabilities the enhanced CN of the 3G systems will
be able to support 4G services (Kaaranen H. , et. al
2001). So, it is expected that the 4G RAN will
undergo the main changes, from the viewpoint of
CN only resource scaling is required. For these
reason it is very important to develop solution
methods for the above-mentioned CN planning
problems. It will enable planning 3G/4G networks
in such a way that both technical and economical
advantages can be achieved when constructing and
exploiting the networks.
In this paper one of the main problems of Core
Network planning is considered in details. This is
the problem of performance evaluation of IM-
subsystem elements. This problem arises because of
the fact that the traffic generated by 3G services
may be self-similar or long-range dependent in
nature (i.e., bursty over a wide range of time
scales).
Self-similarity is observed in different
networks; in particular, in local area networks
(Willinger W. et. al, 1995), Internet (Roberts J.B.,
1998), wireless networks (M. Jiang et. al, 2001) and
others. It is shown in (R. Kalden, S. Ibrahim, 2004)
that in GPRS in the case of aggregated traffic and
also in the case of individual WAP and WEB traffic
traces, the results strongly suggest long-range
dependency (values of the Hurst parameter are
about 0.8). Besides, the packet arrival process of
WAP and WEB traffic may be considered as a class
of processes consisting of the superposition of an
infinite number of ON/OFF-sources. Through the
characterization of the sum of the covariances, it is
possible to establish a simple explicit necessary and
sufficient condition for the process to be long-range
dependent (F. Geerts, C. Blondia, 1998). It is
reasonable to suppose that self-similarity may occur
ICETE 2005 - WIRELESS COMMUNICATION SYSTEMS AND NETWORKS
98

in 3G wireless networks as well. This is in sharp
contrast to commonly made traffic modeling
assumptions, because self-similarity is
characterized by stronger dependence of a variance
from time than linear dependence (R. Kalden, S.
Ibrahim, 2004). The traffic does not smooth out in
the case of aggregation, leading to congestion
situations and packet-drops due to the burstiness of
the traffic. In the case of self-similar traffic the
applied methods for performance analysis and
network dimensioning are different from those
applied to statistically more simple traffic, which
can be modeled with Markovian processes (W.
Willinger et. al, 1997), (A. Adas, 1997). For
example, the queue tail behavior is heavy-tailed in
the case of self-similar input traffic (Norros I,
1994).
Thus, the use of the classic teletraffic theory for
a performance evaluation of packet multiservice
network elements gives essential faults, in
particular, network parameters may be
underestimated (Roberts J.B., 2001), (W. Willinger
et. al, 1994), (W. Stallings,1998). In literature
(Norros I., 1994), (Norros I., 1995), (Addie R.G. et
al.,1998) the approaches of overcoming such sort of
difficulties are considered. In our research the
results from (Norros I, 1995) concerning self-
similar multiservice traffic is developed and applied
for evaluation of probabilistic and time
characteristics of such IM-subsystem element as
Gateway GPRS Support Node (GGSN) for the
UMTS Rel’5 IM-subsystem. The method for GGSN
performance evaluation is based on using the
FBM/D/1/W queueing system.
2 UMTS Rel’5 CORE
NETWORK
ARCHITECTURE ASPECTS
The reference architecture for UMTS Rel’ 4 and
Rel’ 5 from 3GPP TR 23.821 is the same (Kaaranen
H. , et. al 2001). In the development of UMTS Rel’
5 the focus has shifted to the PC CN domain, which
has been extended with IM-subsystem
functionality. The vision of UMTS Rel’5 from the
All IP point of view taken from (Kaaranen H. , et.
al 2001) is shown in Fig. 1. As seen from Fig. 1, the
principle of allocation of data flows between end
users and GGSN leads to increasing of the load on
the network elements while approaching to GGSN.
The GGSN is the node that the most exposed to the
self-similarity influence in UMTS. The most
important events determining the load on GGSN on
the network level are arriving IP packets. Currently,
a transport technology for delivery of IP packets
to/from GGSN is not defined uniquely. For
instance, ATM may be applied as one of the
possible cases of such technology (W. Stallings,
1998).
Figure 1: Vision of UMTS Rel’ 5 (all IP)
3 THE LOAD MODEL
It is assumed that values s(t) of a random process
with interdependent increments are the total load
arrived to the node (server) in the time point t>0.
Current values s(t) in the time interval [0, t) may be
determined by the number of information units
(bytes, ATM cells, IP packets, and so on. If the
corresponding process is ordinary then an
increment is one information unit. The increments
intensity is the rate parameter
λ , 1/s. Realizations of
process s(t) are non-decreasing step functions with
increments taking place in random time points.
Let us consider a random variable
(
)
[
) tTTtsS
T
,0, ⊂
=
=
that is a sample of a random
process s(t). By definition
T
S is a sum of
interdependent identically distributed random
variables. If
0)( >>
=
TSE
T
λ
then conditions of
the central limiting theorem are fulfilled. Here,
(
)
⋅
E
is operator of statistical averaging. Accordingly,
T
S may be approximated by a Gaussian random
variable (Kleinrock L., 1976). Taking into account
abovementioned assumptions
T
S may be defined
as:
xTbTS
T
⋅+= )( λ
,
(1)
where x = N(0,1) is a normalized Gaussian random
variable with the zero mean and the unit variance,
b(T) is a variance of
T
S .
If
ttb
2
)( σ =
and t > 0 then the univariate
probabilities distribution of the process s(t)
coincides with the corresponding distribution of a
Brownian motion process or a displaced Wiener
process (Karatsas I. et. al, 1997), (Papoulis A.,
1984). Similarly, the process s(t) corresponds to a
MS
BTS BSC
ISDN
PSTN
CSPDN
U
m
Network Management (NMS)
GERAN
V
A
S
IN
CAMEL
WAP
CN PS Domain
SGSN GGSN
IP Multimedia
UE
BS RNC
Uu
UTRAN
HSS
IMCN
IP/ATM
IP/ATM
IP/ATM
I
u
MS
BTS BSC
ISDN
PSTN
CSPDN
U
m
Network Management (NMS)
GERAN
V
A
S
IN
CAMEL
WAP
CN PS Domain
SGSN GGSN
IP Multimedia
UE
BS RNC
Uu
UTRAN
HSS
IMCN
IP/ATM
IP/ATM
IP/ATM
I
u
PERFORMANCE EVALUATION OF 3G CORE NETWORK NODES
99

Poisson process if condition (1) is fulfilled when x
is a Poisson random variable and
ttb λ =)( .
It is necessary to take into account a self-
similarity notion when load modeling in packet data
networks. There are different ways of self-similarity
load modeling (W. Willinger et. al, 1997), (Norros
I. et. al, 1995), (Addie R.G. et. al, 1998). With
reference to (1) self-similarity may be taken into
account as
,15.0,)()(
22
<≤= HTTb
H
σ
(2)
where H is the Hurst parameter. Expressions (1)
and (2) specify a model of a total traffic load
arriving to a server input by a time point t=T.
4 THE QUEUEING SYSTEM
MODEL
It is assumed that s(t) arrives to the server input.
The server is modeled by queueing system with
deterministic rate C, 1/sec and the buffer size (W-1),
∞<≤ W1 . The queueing system is the stable one
because there is a stationary probability distribution
if C >
λ . In accordance with the Kendall’s notation
for queues the system is G/D/1/W (Kleinrock L.,
1975). The corresponding system may be also
defined as FBM/D/1/W (Norros I, 1995) if the
expressions (1,2) are fulfilled. Here, the FBM is a
normalized fractional Brownian motion, i.e. the
corresponding process is a strictly self-similar one.
5 THE TASK ESTIMATION
DEFINITION
When stability conditions are fulfilled the average
value of the total load arrived to the queueing input
by the time point t=T>0 is less than the queueing
system can serve for the same time interval. It
should be emphasized that the load is a random
process. Therefore, it is possible to appear an event
when the buffer will be overflow. The probability
of the event is defined by statistical properties of an
unserved traffic process that may be written as
[]
CttStV −= )(,0max)(
(3)
The introduction of operator max [0, x] in (3) is
caused by nonnegative values of an unserved load.
It is similar to the introduction of an adsorbing
barrier in the coordinate origin point for the
displaced self-similar (fractional) Wiener process.
The estimation problem is to determine values of
parameters C and W. It should be done by taking
into account the following condition. The
probability that the unserved load will be greater
than the parameter W must not exceed the preset
threshold
ε
:
[
] 10,)( <<<>
=
>
ε
ε
ε
tWtVP
(4)
6 THE TASK ESTIMATION
DEFINITION
Taking into consideration the approximation of the
random process s(t) sample by the random Gaussian
variable defined by the expressions (1,2) we have
the lower bound for the buffer saturation
probability
[
]
[
]
)(max)(
0
TxPWtVP
T
α
>≥>
>
,
(5)
where
(
)
[
]
H
TWTCT )()(
2
σλα +−= .
The expression (5) shows that the probability of
events union is not less than the probability of each
event. Taking into account that the random variable
X is the normalized displaced Gaussian random
one, the expression (5) may be transformed as
[]
[]
)2/)(exp(5.0max
2/)2/exp(max)(
2
0
2
)(
0
T
dxxWtVP
T
T
T
α
π
α
−≈
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−≥>
>
∞
>
∫
(6)
Let us take into consideration the logarithmic
function monotony for the expression that is
equivalent (4,6). Then the expression binding the
parameters C, W, λ and the buffer saturation
probability
ε
is
(
)
(
)
()
H
T
T
WTC
2
2
2
0
minln
σ
λ
ε
+−
≈−
>
(7)
The solution of the equation (7) may be found
by the parameter T differentiation and equating of
the obtained derivative with zero (Norros I, 1995).
It gives the following expression
()()
()()
()
H
T
m
T
WTC
CH
WH
T
2
2
2
0
minarg
1
σ
λ
λ
+−
=
−−
=
>
(8)
Substituting T
m
in (7) and transforming the
expression we finally get
,15.0,
)1(
ln2
1/
/1
1
1
<≤
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
+=
−
−
H
H
HW
nC
H
H
HH
ε
λ
(9)
where
λσ /
2
=n .
Substituting n, W, λ and
ε values in (9) we get
the upper bound (if H=0.8) and lower bound (if
ICETE 2005 - WIRELESS COMMUNICATION SYSTEMS AND NETWORKS
100

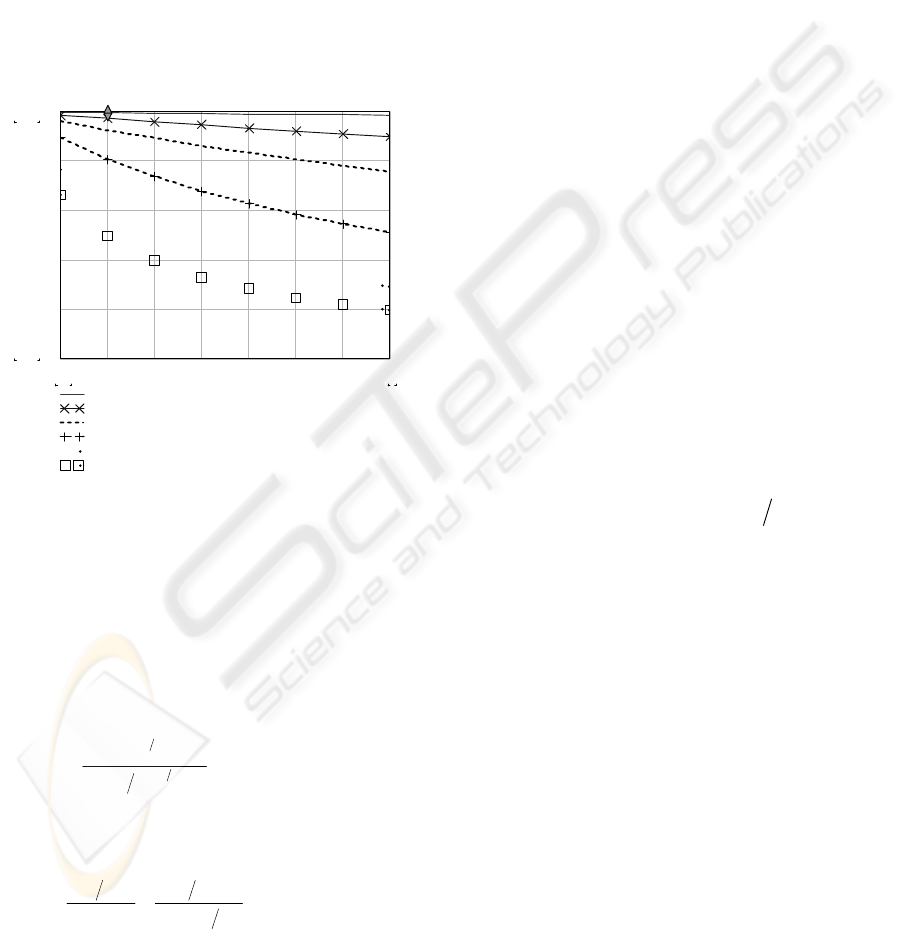
H=0.5) of the server service rate C. One of the main
parameters of queueing system is the inverse
parameter (9)
ρ = λ/ C called the utilization factor.
Fig. 2 illustrates dependences of the utilization
factor from the magnitude
λσ /
2
=n
for various
values of the Hurst parameter and the buffer
capacity W when
ε
= 10
-5
.
Trends of the curves (Fig.2) show that it is very
important to take into account the self-similarity
influence while assigning server parameters. It
should be emphasized that the area of the
dependences when n=1 and H=0.5 (as shown in
Fig.2) corresponds to the case of the Poisson arrival
process.
0.998
0.198
p1 n()
p2 n()
x1 n()
x2 n()
z1 n()
z2 n()
4
0.5 n
0.5 1 1.5 2 2.5 3 3.5 4
0
0.2
0.4
0.6
0.8
H=0.50 W=1500
H=0.50 W=200
H=0.65 W=1500
H=0.65 W=200
H=0.80 W=1500
H=0.80 W=20
0
Utilization factor
Figure 2: Self-similarity influence on the server
utilization factor
It is wise to take the value
ε
sufficiently small.
It enables to have the acceptable probability of
messages blocking arriving on the server. In this
case the server buffer will be filled partly.
For determination of the upper bound of the
average queue length in the server buffer the
expression based on results (Norros I., 1994),
(Norros I. et. al, 1995) may by used:
()
(
)
()
()
HH
H
C
C
q
−
−
−
=
1
121
max
1
/
λ
λ
(10)
The classical result for M/D/1 system may be
applied for determination of the lower bound of the
average queue length:
()
)1(2/1
2
min
C
C
C
C
q
λ
λ
λ
λ
−
−
−
=
(11)
The upper and the lower bounds for average
service time (
τ ) are determined using Little result
(Kleinrock L., 1976):
CqCq /,/
minminmaxmax
=
=
τ
τ
,
(12)
Thus, using the expressions (9-12) it is possible
to determine bounds for the probabilistic and time
characteristics of the single server under the self-
similarity load influence.
7 CASE STUDY
In this section the example illustrating the above-
presented method is considered. Since there are no
exact regulations on transport network protocols on
Serving GPRS Support Node (SGSN)-GGSN
interface at the present moment it is assumed that
ATM is used as underlying technology for delivery
of IP packets. The rate of information units (ATM
cells) arriving on SGSN is multiple (k) of 2
Mbit/sec. The parameters characterizing the server
normal functionality may be estimated by the
following way.
Let k = 20 and in average 30% of the channel
throughput is in use during the messages delivery to
SGSN. Then, the value of the intensity of ATM
cells arriving on the SGSN input is
λ ≈ 30000 s
-1
. If
a number of SGSNs connected to the GGSN is 4
then the total value of the intensity of ATM cells
arriving to GGSN input is
λ ≈ 120000 s
-1
. In
accordance with (4.8), (4.9) and (4.10) the
relationships between the GGSN server capacity,
the upper bound for average queue length in the
GGSN buffer, the upper bound for the average
service time of information units in the GGSN
buffer and the parameter n
)(
2
λσ =n
are shown
in Figures 3, 4, 5 respectively (W = 50, 200; H =
0.8;
ε = 10
-7
).
8 CONCLUSION
In this paper the influence of self-similar input on
GGSN performance in UMTS Rel’5 IM-subsystem
has been analyzed. FBM/D/1/W queueing system
for evaluation of the GGSN parameters was
applied. The submitted method enables determining
the following probabilistic and time characteristics:
•
upper and lower bounds for the GGSN
service rate;
•
upper and lower bounds for the average
queue length in the GGSN buffer;
•
upper and lower bounds for the average
service time of information units in the
GGSN buffer;
PERFORMANCE EVALUATION OF 3G CORE NETWORK NODES
101

• the server utilization.
The obtained results point to a need to take into
account self-similarity while assigning the GGSN
parameters.
As well known, when providing multimedia
services based on IP technologies one of the main
aspects is to ensure Quality of Service (QoS). From
this point of view the presented method may be
extended for performance evaluation of other IM-
subsystem elements, in particular, for on Serving
GPRS Support Node (SGSN) performance
evaluation.
0246810
1
.
10
5
1
.
10
6
1
.
10
7
W=50 H=0.8
W=200 H=0.8
n
C
Figure 3: GGSN server capacity estimating
0246 810
1
.
10
4
1
.
10
3
0.01
0.1
1
10
100
W=50 H=0.8
W=200 H=0.8
n
q (max)
Figure 4: The upper bound for average queue length in
the GGSN buffer
0246 810
1
.
10
7
1
.
10
6
1
.
10
5
1
.
10
4
1
.
10
3
0.01
0.1
W=50 H=0.8
W=200 H=0.8
n
T (max), ms
Figure 5: The upper bound for the average service time in
the GGSN buffer
REFERENCES
Kaaranen H., Ahtiainen A., Laitinen L., Naghian S.,
Niemi V. UMTS Networks. Architecture, Mobility
and Services, John Wiley & Sons, 2001.
Bale M.C. Voice and Internet multimedia in UMTS
networks, BT Technology Journal, Vol. 19, No.1,
2001.
Y.Yamao, H. Suda, N.Umeda, N. Nakajima, “Radio
access network design concept for the fourth
generation mobile communication system,” Proc.
VTC2000-Spring, vol. 3, pp. 2285-2289, 2000.
“The UMTS 3G Market Forecasts – Post September 11,
2001,” Report # 18 from the UMTS Forum, February
2002.
M. Jiang, M. Nicolic, S. Hardy, L. Trajkovic, “Impact of
self-similarity on wireless data network
performance,” ICC 2001, USA, June 2001.
K. Park, W. Willenger, “Self-Similar network traffic and
performance evaluation,” John Wiley & Sons, 2000.
R. Kalden, S. Ibrahim, “Searching for self-similarity in
GPRS”, Proceedings of the 5th anuual Passive &
Active Measurement Workshop (PAM2004), Antibes
Juan-les-Pins, France, April 19-20, 2004
V. Paxson, S.Floyd, “Wide Area Traffic: the failure of
Poisson Modeling,” Proceedings of ACM
SIGCOMM’94, 1994.
Willinger W., Taqqu M.S., Leland W.E., Wilson D.V.
Self-similarity in high-speed packet traffic: analysis
and modeling of Ethernet traffic measurements,
Statistical Science, vol. 10, no. 1, 1995, pp. 67-85.
Roberts J.B. Traffic Theory and the Internet, IEEE
Communications Magazine, January 2001, pp.94-99.
F. Geerts, C. Blondia, “Superposition of Markov sources
and long range dependence”, The 4th International
Conference on Broadband Communications (BC '98),
pp. 550-562, 1998.
W. Willinger, M.S. Taqqu, R. Sherman, D.V. Wilson,
“Self-similarity through high-variability: statistical
ICETE 2005 - WIRELESS COMMUNICATION SYSTEMS AND NETWORKS
102

analisis of Ethernet LAN traffic at the source level,”
IEEE/ACM Transactions on networking, vol. 5, no. 1,
pp. 71-86, February 1997.
A. Adas, “Traffic Models in Broadband Networks,”
IEEE Communicatios Magazine, pp. 82-89, July
1997.
Norros I. A storage model with self-similar input,
Queueing Systems, vol. 16, 1994, pp. 387-396.
W. Willinger, D. Wilson, M. Taqqu, “Self-similar traffic
modeling for high-speed networks,” ConneXions,
November 1994.
W. Stallings, “High speed networks. TCP/IP and ATM
design principles,” Upper Saddles River, NJ:
Prentice-Hall, p. 576, 1998.
Norros I. On the Use of Fractional Brownian Motion in
the Theory of Connectionless Networks, IEEE Journal
on Selected Areas in Communications, vol. 13, № 6,
August 1995, pp. 953-962.
Addie R.G., Zukerman M., Neame T.D. Broadband
Traffic Modeling: Simple Solutions to Hard
Problems, IEEE Communications Magazine, August
1998, pp. 88-95.
Kleinrock L. Queueing Systems, volume II. Computer
Applications, John Wiley & Sons, 1976
Karatsas I., and Shreve S., Brownian Motion and
Stochastic Calculus, 2nd ed, New York: Springer-
Verlag, 1997.
Papoulis A. Probability, Random Variables, and
Stochastic Processes, 2nd ed., New York, McGraw-
Hill, 1984.
Kleinrock L. Queueing Systems, volume I. Theory, John
Wiley & Sons, 1975.
Norros I., Simonian A., Virtamo J. The Benes method – a
unified approach to ATM FIFO queueing, New
Telecommunication Services for Developing
Networks, Proceedings of St. Petersburg International
Teletraffic Seminar, St. Petersburg, 25 June-2 July,
1995, pp. 431-449.
PERFORMANCE EVALUATION OF 3G CORE NETWORK NODES
103