DESIGN ISSUES FOR ELECTRONIC AUCTIONS

Jarrod Trevathan and Wayne Read

School of Mathematical and Physical Sciences

James Cook University

Hossein Ghodosi

School of Information Technology

James Cook University

Keywords:

Auction security, anonymity, authentication, price determination, payment enforcement, group signatures.

Abstract:

Extensive research has been conducted in order to improve the security and efﬁciency of electronic auctions.

However, little attention has been paid to the design issues. This paper discusses design issues and contrasts

the differing security requirements between various auction types. We demonstrate that poor design for an

electronic auction breaches the security of the system and degrades its practicality, irrespective of how se-

cure/efﬁcient the building blocks of an electronic auction are. This is accomplished by illustrating design

ﬂaws in several existing electronic auction schemes. Furthermore, we provide a solution to these ﬂaws using

a group signature scheme and give recommendations for sound auction design.

1 INTRODUCTION

An auction is an exchange mechanism whereby a

seller (or sellers) offers an item for sale and many

bidders submit bids in competition for the item. The

Auctioneer organises the auction on behalf of the

seller and accepts bids from the bidders. The Auc-

tioneer attempts to maximise the sale price for the

seller, whereas the bidders try to win the item for the

lowest price possible. An electronic auction is a cryp-

tographic protocol designed to securely and anony-

mously conduct auctions. While extensive research

has been undertaken for improving the security and

efﬁciency of electronic auctions, (see (Cachin, 1999;

Franklin and Reiter, 1996; Kikuchi et al., 1998; Naor

et al., 1999; Trevathan, 2005)), little attention has

been paid to the design issues. In this paper we

demonstrate that poor design for an electronic auc-

tion breaches the security of the system and degrades

its practicality regardless of how secure/efﬁcient the

building blocks of an electronic auction are. This

is accomplished by illustrating design ﬂaws in sev-

eral existing auction schemes. We also provide solu-

tions to these ﬂaws using a group signature scheme

and give some recommendations for sound auction

design.

This paper is organised as follows: Section 2 gives

a general background on electronic auction schemes.

Section 3 describes the security problems inherent in

conducting electronic auctions. Section 4 discusses

design issues and illustrates some major design ﬂaws

in several existing schemes. Section 5 gives some rec-

ommendations about how these ﬂaws can be ﬁxed and

suggestions regarding good auction design principles.

Section 6 provides some concluding remarks.

2 TYPES OF AUCTIONS

There are many types of auctions, including English,

Vickrey, Dutch, and Continuous Double auctions (see

Figure 2). An English auction is the most prominently

known type of auction and is commonly used in real

estate. In this auction there is one seller who offers an

item for sale. Many potential buyers submit bids in

an attempt to win the item. The winner is the highest

bidder after a given time-out period.

An alternative to this is the Vickrey auction. This

is referred to as a sealed bid, second price auction.

It is comprised of bidders submitting their bids se-

cretly during a bid submission round. The bids remain

sealed until a winner determination round, where the

Auctioneer views all of the bids and awards the auc-

tion to the highest bidder. In this auction, the win-

ner only has to pay the second highest price, i.e., the

highest losing bid. The values of all other losing bids

remain secret. In contrast, an English auction is an

open bid, ﬁrst price auction.

340

Trevathan J., Read W. and Ghodosi H. (2005).

DESIGN ISSUES FOR ELECTRONIC AUCTIONS.

In Proceedings of the Second International Conference on e-Business and Telecommunication Networks, pages 340-347

DOI: 10.5220/0001419103400347

 SciTePress



single double

sealed open

ascending descending

Vickrey English Dutch CDA

Figure 1: Taxonomy of Electronic Auction Schemes

In a Dutch or descending auction, the seller pro-

gressively lowers his/her bid until a buyer accepts.

The winner is the ﬁrst buyer to accept the seller’s of-

fer. They must pay an amount equal to this bid. In

this respect Dutch auctions have the natural property

of concealing the losing bid values. This form of auc-

tioning is also referred to as descending, as unlike an

English auction, the winning price is bid downwards

rather than up.

A further style of auction used in share markets is

a Continuous Double Auction (CDA). The aforemen-

tioned auctions have only one seller and many buyers.

CDAs on the other hand, have many buyers and many

sellers who continuously trade a particular commod-

ity. These auctions are open bid and the price can be

either ascending or descending.

Electronic auction schemes have been proposed for

all of these auction types. However, regardless of the

auctioning mechanism, all schemes consist of the fol-

lowing stages:

Initialisation: The Auctioneer sets up the auction and

advertises it (i.e., description of good, starting time,

etc).

Registration: In order to participate in the auction,

bidders must ﬁrst register with the Auctioneer (or a

registration manager). This ensures only valid bids

are made and bidders can be identiﬁed for payment

purposes. It is desirable for registration to be a one-

off procedure. When a bidder has registered they are

able to participate in any number of auctions rather

than re-registering for each new auction.

Bidding: A registered bidder computes his/her bid

and submits it to the Auctioneer. The Auctioneer

checks the bid received to ensure conformity with the

auction rules.

Winner Determination: The Auctioneer determines

the winner according to the auction rules. It is desir-

able for this process to be publicly veriﬁable.

3 AUCTION SECURITY

In recent years, many companies have emerged offer-

ing auctioning services via the Internet (e.g., eBay

and onSale

). Such sites lack security for both the

seller and the bidder and moreover require all parties

to trust the Auctioneer. Furthermore, the identities

and information relating to the participants is open to

abuse. Common problems identiﬁed include: the bid-

ders repudiating bids (i.e., they win and later decide

they don’t want to pay), the seller not delivering the

item and Auctioneer corruption by awarding the auc-

tion to someone other then the legitimate winner.

Security and anonymity has been addressed in

literature by (Cachin, 1999; Franklin and Reiter,

1996; Kikuchi et al., 1998; Naor et al., 1999;

Trevathan, 2005). Additionally, numerous auction

schemes have been proposed in an attempt to solve

the aforementioned problems. There are differing

security requirements depending on whether the

auction is sealed or open bid. However, in general,

most schemes in literature agree on the following

security goals:

Unforgeability - Bid must be unforgeable, otherwise

a bidder can be impersonated.

Non-Repudiation - Once a bidder has submitted a

bid they must not be able to repudiate having made

it. For example, if a bidder wins and does not want to

pay they might deny that they submitted the bid.

Anonymity - The bidder-bid relationship must be

http://www.ebay.com

http://www.onsale.com

DESIGN ISSUES FOR ELECTRONIC AUCTIONS

341

concealed so that no bidder can be associated with the

bid they submit.

Public Veriﬁability - There must be publicly avail-

able information by which all parties can be veri-

ﬁed as having correctly followed the auction protocol.

This should include evidence of registration, bidding

and proof of winner/loser.

Robustness - The auction process must not be af-

fected by invalid bids nor by participants not follow-

ing the auction protocol correctly.

4 DESIGN ISSUES

The main design goals discussed previously in the lit-

erature of electronic auctions include fairness, efﬁ-

cient registration, efﬁcient bidding, and efﬁcient win-

ner determination (see, for example, (Boyd and Mao,

2000; Franklin and Reiter, 1996; Naor et al., 1999;

Boyd et al., 2000; Trevathan, 2005)). Our observation

is that despite all components of an electronic auction

functioning correctly, there is still no guarantee that

the whole system works properly. In this section we

discuss several design issues that must be considered

in order to achieve a practical auction system.

4.1 Trust Issues

Auctioneer corruption is a major problem in elec-

tronic auctions. A malicious Auctioneer might inﬂu-

ence the auction proceedings in a manner inconsis-

tent with the auction rules. For example, the Auction-

eer might choose to block bids, insert fake bids, steal

payments, proﬁle bidders, open sealed bids prior to

the winner determination phase, or award the item to

someone other than the legitimate winner. Further-

more, the Auctioneer may be in collusion with some

of the bidders.

In general, all schemes can be classiﬁed according

to how they deal with this problem. We have identi-

ﬁed the following trust models:

Auctioneer Trust - This is the easiest (and the most

unacceptable) solution to the problem. It is assumed

that the Auctioneer is trustworthy and honestly

follows the protocol. This is the strategy employed

by all Internet auction sites as it easily solves many

relevant problems (e.g., security, anonymity, etc.).

However, all bidders are at the mercy of the company

running the auction.

Trusted Third Party - Since the Auctioneer is a

beneﬁciary, the assumption that it follows the auction

protocol is unrealistic. An alternative could be that

the bidders and Auctioneer provide a trusted third

party (TTP) with information so that when there is a

dispute the TTP can be called upon to resolve it (see

(Boyd et al., 2000)). However, such a setup requires

all parties to have conﬁdence in the TTP who is an

attractive security target and a bottleneck.

Threshold Trust - Threshold trust schemes protect

against a corrupt Auctioneer by distributing the role

of the Auctioneer across ℓ servers (see (Franklin and

Reiter, 1996; Sakurai and Miyazaki, 1999)). The auc-

tion can be considered secure/fair unless a threshold

t, 1 ≤ t ≤ ℓ of the Auctioneers collude. The value of

t is usually around ℓ/3.

Such a scheme is clearly better then the previous

approaches as no single party acting maliciously can

inﬂuence the auction proceedings. However, thresh-

old trust requires much communication between

bidders and the auction servers, as well as between

the auction servers themselves. Furthermore, when

the auctioning company is small, collusion among

Auctioneers is beneﬁcial to the group as a whole.

Two-Server Trust - An alternative approach to

threshold trust is to split the auctioning responsibility

among two servers owned by separate entities (see

(Cachin, 1999; Naor et al., 1999)). Here the auction

result can be trusted as long as the two entities do

not collude. Two-server trust schemes effectively

reduce the communication overhead involved in

threshold trust schemes and thus far have proven

to be computationally efﬁcient. However, if one of

the two servers decides not to co-operate, then the

auction outcome cannot be determined.

Distributed Trust - In this approach the bidders

jointly calculate the auction result without the help

of an Auctioneer. The merit of such an approach is

that collusion amongst bidders is prevented unless all

bidders are corrupt, which negates the reason for col-

luding in the ﬁrst place (see (Brandt, 2003)).

Distributed trust schemes are unrealistic as they re-

quire all bidders to participate during the winner de-

termination phase. Such an approach is not feasible

when the number of bidders is large. Furthermore,

distributed trust is not applicable to CDAs as this as-

sumes knowledge of the total number of bidders prior

to the start of bidding. In a CDA, new bidders are

entering the auction all the time. Using a distributed

bidder approach would require communicating new

information to all the auction participants every time

a new bidder registers.

4.2 Anonymity Issues

Another important criteria for the evaluation of secure

electronic protocols is anonymity. This is important

because the bidder-bid relationship must be concealed

in such a way that no bidder can be associated with the

ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS

342

bid they have submitted. There are several different

approaches to satisfy this requirement. For example,

auction protocols which utilise secure computation

for winner determination (e.g., (Kikuchi et al., 1998;

Harkavy et al., 1998) provide this facility by conceal-

ing the identity of bidders in their bids). A common

solution is to issue bidders with a pseudonym (during

registration), which they can use to submit bids. That

is, bidders register themselves (by presenting veriﬁed

identiﬁcation) and obtain a pseudonym.

Seemingly the technique of issuing pseudonyms

requires having more than one server/party on the

auction side. Otherwise, the same party issuing

the pseudonym knows the real identity of the asso-

ciated bidder, and thus learns the relationship be-

tween the bids and the bidders. On the contrary, if

the pseudonym issuer does not know the pseudonym

(e.g., it is issued by blindly signing a message), then it

cannot retrieve the real identity of a bidder in the case

of a dispute. This model essentially works as follows

(assume the two servers/parties are called S

and S

1. Bidders present their identiﬁcation to S

and obtain

a token that does not carry their ID.

2. Bidders submit the token (without revealing their

ID) to S

, who issues a pseudonym associated with

the token.

In this way, neither S

nor S

knows the relation-

ship between any real ID and the pseudonyms. The

bidder then submits his/her bid using the pseudonym.

However, in the event of a dispute S

and S

can co-

operate to determine the real ID associated with each

pseudonym.

Our observation is that, regardless of how se-

cure the anonymity issuing protocol is, the resulting

scheme is not secure if there is no separation between

the registration and the bidding phases. That is, the

registration must be performed for all bidders prior to

the commencement of bidding and the system must

not accept any bid before the registration is closed.

The following scenario explains a possible attack: A

bidder provides identiﬁcation to S

and obtains a to-

ken. Using this token, it obtains a pseudonym which

can be used for bidding. If there is no separation

between the registration and bidding phases S

can

act in a procrastinating manner by halting all future

registrations until the newly registered bidder sub-

mits his/her bid. This scenario enables S

to learn

the mapping between the bidder’s identity and his/her

pseudonym. To protect against this type of attack, the

scheme should not allow any bidding prior to the reg-

istration closing time.

Note that there are electronic auction schemes in

which it is impossible to have a separation between

the registration and the bidding phases. For example,

a CDA allows bidders to continuously submit bids at

the same time new bidders are being registered (i.e.,

the registration and bidding phases overlap). There-

fore the scheme by Wang and Leung (Wang and Le-

ung, 2004) can be broken using this procrastinating

attack.

4.3 Bid Authentication Issues

Efﬁcient winner determination is an important crite-

ria in the evaluation of electronic auction protocols.

Because of its importance, many schemes provide ev-

idence to support their claims regarding the ability of

their system to efﬁciently process bids. For example,

(Franklin and Reiter, 1996) in their highly referenced

work, claim that:

“We have implemented a prototype of our ser-

vice to demonstrate its feasibility. The perfor-

mance of this implementation indicates that our

approach is feasible using off-the-shelf worksta-

tions for auction servers, even for large auctions

involving hundreds of bids.”

The question is, what will happen if a (set of) ma-

licious bidder(s) issues too many bids? Optimisti-

cally assuming that processing each bid takes only

one second, then the winner determination process

will require a proportional amount of time (i.e., the

system is not practical). The problem is more crucial

in schemes which use secure computation (see, e.g.,

(Kikuchi et al., 1998)). They achieve anonymity by

concealing the identity of bidders in their bids. In ad-

dition, all bids are submitted anonymously. The win-

ner determination protocol opens only one bid –a bid

that contains the highest offer. If there is a tie (i.e.,

more than one bid at the highest offer), then another

round of bidding must occur. A malicious bidder can

easily cause a never ending scenario in this scheme.

For example, even if all high valued bids are opened

(which is disallowed by the protocol), the Auctioneer

cannot determine who has submitted the bid as it con-

tains a false identity. Obviously, such schemes are not

practical at all.

This problem can be avoided if the bids have

been authenticated. That is, the Auctioneer accepts

bids only from registered bidders (generally, in

all sealed-bid auctions, each bidder submits only

one bid). If the system supports anonymity of the

bidders, then it must also provide the authentication

of the corresponding pseudonym. Note that there

are schemes which check the validity of the bids

(i.e., they check whether the submitted bid satisﬁes

a predetermined structure). This is insufﬁcient,

as one may submit too many well-structured bids.

Furthermore, bid authentication must be secure about

relevant attacks. In order to illustrate the problem,

let us examine the protocol by (Boyd et al., 2000),

which supports a sealed bid auction system. This

is possibly the only auction scheme which uses bid

DESIGN ISSUES FOR ELECTRONIC AUCTIONS

343

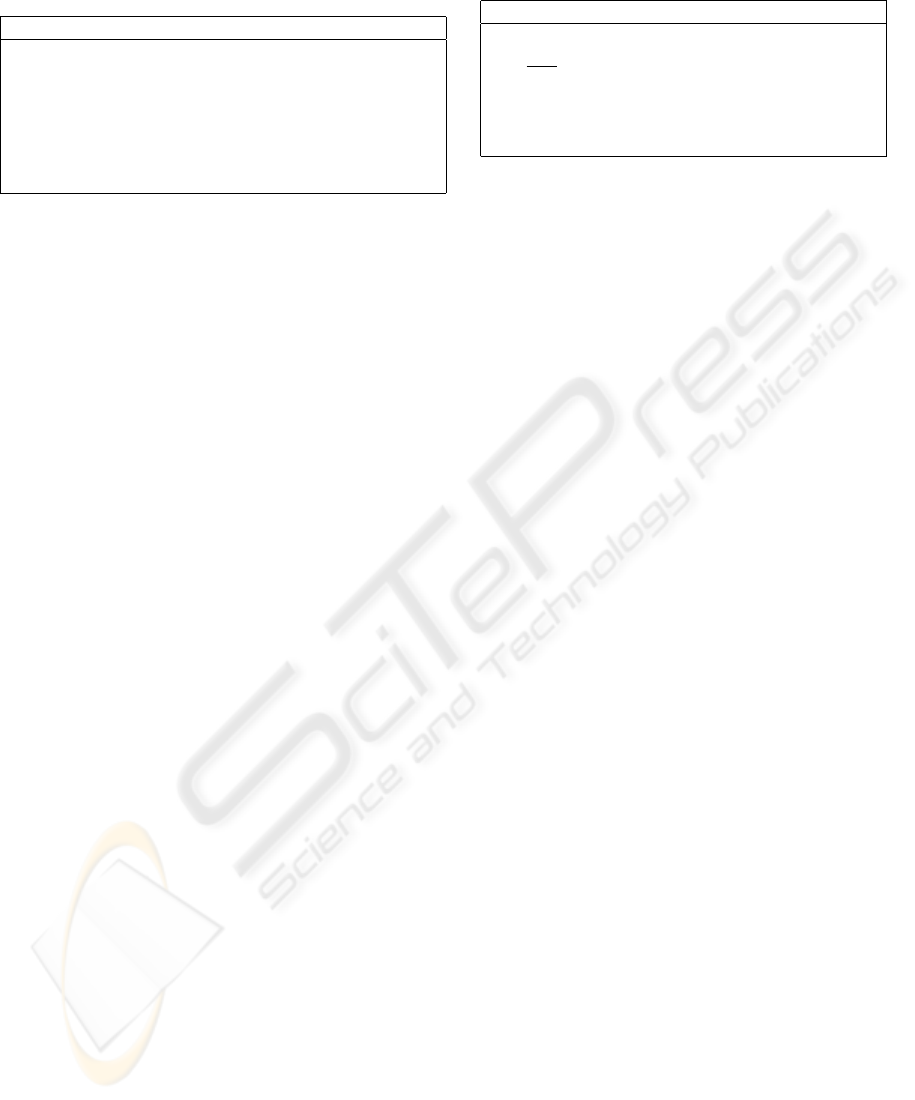
Table 1: The Sealing Protocol

Bidder Auctioneer

a, d

, d

∈

∗

S = g

, B = g

S,B

−→

←− c ∈

= d

− cx

, s

= d

− cx

= s

− bc, t

= s

− ac

−→

= (Sy

)

authentication. But, as we will show shortly, it is

subject to an impersonation attack.

System Settings in (Boyd et al., 2000) -

G is a subgroup of order q in Z

∗

, such that p = 2q +1

for sufﬁciently large prime p. There are two gener-

ators, g

, and g

, such that nobody knows log

The public keys of a bidder b

are certiﬁed to be

= g

and y

= g

Sealing Protocol in (Boyd et al., 2000) -

This is an interactive protocol between the bidder

and the Auctioneer. At the end of this protocol,

the Auctioneer will be convinced that the bidder

submitted a correct bid which can be opened at the

bid-opening phase (in their scheme, the help of the

bidder is necessary to open the bid). A bidder, b

with public keys y

= g

and y

= g

wishes

to commit himself/herself to the bid value b. The

protocol has three steps and works as shown in

Table 1.

To open the bid (at the bid-opening phase) the bid-

der should release the tuples (b, a). This tuple can

be checked with corresponding values at the bid seal-

ing protocol, and upon veriﬁcation, the value b is

the bid submitted by bidder b

. If a bidder refrains

from opening his/her bid (e.g., when he/she learns

that his/her bid is too much higher than the others),

the identity of this person can be traced and suitable

action will be taken. The idea behind this protocol is

that the tuple (S, B, c, t

, t

) is unique, and thus the

bidder is committed to the bid value b. The authors

also proposed a non-interactive version of this proto-

col (see (Boyd et al., 2000)).

Anyone that does not know the secret keys x

and

, cannot participate in, and complete the proto-

col successfully. The impersonation attack works as

shown in Table 2 (the non-interactive version is also

subject to this attack).

The consequence of this attack is that an innocent

bidder b

will be accused of not participating in the

bid opening protocol. But, in fact, nobody knows the

relevant tuple (b, a) for this case (if solving the Dis-

Table 2: The Sealing Protocol by a Malicious Bidder

Bidder Auctioneer

, t

∈

∗

S =

, B = g

S,B

−→

←− c ∈

−→

= (Sy

)

crete Logarithm problem is hard).

4.4 Price Determination Issues

Many auction schemes impose a price list on bidders

(e.g., (Harkavy et al., 1998; Sakurai and Miyazaki,

1999)). This is essentially a series of bidding points

, w

, ..., w

) where w

< w

< ... < w

which a

bidder must choose from.

The scheme by (Harkavy et al., 1998) requires bid-

ders to submit a bid value for each point in the price

list. Meaning, for each point in the price list, a bid-

der must either bid his/her id or a nullifying value.

For a price list of size k, this requires a bidder to sub-

mit k individual values. In some types of auctions

(such as CDAs), a price list may be too restrictive as

bidders require ﬂexibility in choosing their bid. In

some instances this may be down to fractions of cents.

Adding more bidding points comes at the cost of in-

creased computation and communication overhead.

So the question here is what is the correct value of

k to choose?

Moreover, two colluding bidders can continually

bid at the highest price level and cause inﬁnite rounds

of auctioning (i.e., denial of service attack). This is

a major problem with the schemes of (Harkavy et al.,

1998) and (Sakurai and Miyazaki, 1999). For exam-

ple, if the highest price in the list is k and two bidders

bid at this price, then the auction goes to a second

round of bidding. In this round the maximum value in

the price list increases to k × 2. However, both bid-

ders then bid k × 2. This then forces a third round of

bidding and the maximum value in the price list in-

creases to k × 3, etc. If the bidders continue in this

manner, the auction continues indeﬁnitely.

In addition, many schemes using a price list, also

require bidders to participate in a disavowal protocol

(e.g., (Sakurai and Miyazaki, 1999)). This requires

the bidder to engage in a protocol with the Auctioneer

to show that the bid they submitted is not for that par-

ticular price. Upon completion of disavowal for the

respective price level, the Auctioneer selects the next

price in the list and the process repeats. Unfortunately

disavowal protocols are very expensive as much com-

munication must take place to determine the winner.

ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS

344

Furthermore, if some bidders do not participate they

are instantly incriminated, or the auction process is

left in an inconsistent state.

For the reasons stated above, schemes using price

lists tend to be restrictive and are not always practical

for certain types of auctions.

4.5 Payment Issues

A major issue in electronic auction schemes is how to

enforce payment from the winning bidder(s). Previ-

ous schemes have achieved this by using digital cash

schemes. For example, Franklin and Reiter (Franklin

and Reiter, 1996) use a digital coin to represent a bid-

der’s bid. The value of the coin is equivalent to the

amount of the bid. The winner’s coin is deposited into

the seller’s bank account at the end of the protocol. In

this scheme the purpose of the coin is to prevent re-

pudiation of bids. The scheme by (Boyd et al., 2000),

uses a digital cash scheme in a similar manner. When

a bidder repudiates a bid, the identity of the bidder

can be recovered by presenting the bidder’s piece of

digital cash to the bank.

We believe that using digital cash does not sig-

niﬁcantly enhance the security of an electronic auc-

tion scheme. Instead it introduces another party (i.e.,

the bank) to the auction which must be trusted by

the participants. This complicates auction schemes

and makes it increasingly difﬁcult to analyse how se-

cure the scheme is. Franklin and Reiter (Franklin

and Reiter, 1996) claim that their scheme can provide

anonymity through the use of pseudonyms. However

even if this is done, anonymity is still dependent on

the underlying digital cash scheme.

The main goal of digital cash is to allow a spender

to engage in anonymous and untraceable transactions

with a merchant. When the spender breaks the rules

(i.e., repudiates the purchase or double spends the

cash) the only means of recourse is for the bank to re-

veal the spender’s identity. In terms of an anonymous

auction, we are only interested in revealing a bidder’s

identity when there is a dispute (i.e., bid repudiation).

Unless the bank is built into the auctioning model (as

in (Boyd et al., 2000)), other more efﬁcient mecha-

nisms for identity escrow can be used rather than dig-

ital cash schemes.

5 RECOMMENDATIONS

This section provides some suggestions of ways to

ﬁx the problems raised in the previous section and

discusses good design strategies for electronic auc-

tions. Surprisingly there already exists cryptographic

mechanisms to solve many of the problems facing

electronic auctions. However, little if any of the lit-

erature on electronic auctions has embraced this re-

search. The proposed solution comes from group sig-

nature schemes.

A group signature scheme allows members of a

group to sign messages on behalf of the group so that

no one can work out which particular user is the signer

(see (Anteniese et al., 2000)). A signature on a mes-

sage can be veriﬁed by anyone using a single public

key. When there is a dispute (i.e., someone repudiates

having signed a message) a trusted group manager can

reveal the identity of the signer of a message. Each

signature is unlinkable and no coalition of users (even

with the help of the group manager) is able to forge a

valid signature of an innocent user.

Group signatures have many desirable properties

with regard to electronic auctions. In an auction, each

bidder belongs to a group of bidders. Every bidder

has a unique signature which enables them to sign

bids anonymously. The bidders submit their bids to

the Auctioneer, who can then verify each signature

using the group’s public key. However, the Auction-

eer cannot solely be the group manager as this would

require all bidders to implicitly trust that the Auction-

eer would not reveal their identities. Instead this task

must be distributed among the Auctioneer and an-

other party (e.g., a registration manager). When there

is a dispute, both the Auctioneer and the other party

must cooperate in order to reveal the identity of whom

signed the bid in question.

In the subsections that follow, we will address each

of the design issues stated in the previous section

and describe how the properties of group signature

schemes can be employed. Throughout this section,

we develop a model for electronic auction design.

This model is not speciﬁc to any particular auction

type, but can be used as a general basis for all types

of auctions. Note that mechanisms for sealing bids

will not be discussed. Instead the model addresses

trust, anonymity, bid authentication, price ﬂexibility

and payment enforcement.

5.1 Trust

Using publicly veriﬁable protocols reduces the trust

required in the Auctioneer. This approach allows all

parties (even outsiders) to view the auction process

and they can verify that the auction outcome is cor-

rect.

Many schemes use public bulletin boards to serve

this purpose (Sakurai and Miyazaki, 1999; Boyd et

al., 2000; Wang and Leung, 2004). An Auctioneer

can post bids and auction results on the board so that

all others can verify the auction proceedings. It is as-

sumed that only the Auctioneer can write to this board

and that it is publicly accessible to all parties.

DESIGN ISSUES FOR ELECTRONIC AUCTIONS

345

Public bulletin boards have implications for sealed

bid auctions as the main requirement is to keep the

losing bids secret. However, in all sealed bid auc-

tion schemes it is inevitable that bidders learn statis-

tics about the bids submitted (i.e., highest price, bid

values, etc). Therefore, using a bulletin board is suf-

ﬁcient for sealed bid auctions, as long as the bidder-

bid relationship remains secret (i.e., bidders cannot be

linked to their bids).

However, even if publicly veriﬁable protocols are

used there is still some need to trust the Auctioneer.

In this case, the best approach is to use the two-server

trust model (see Section 4.1). This needs to be mod-

iﬁed slightly in that the second party is only required

in the case of a dispute but cannot act on his/her own

(as in the case of the TTP approach). This will be

clariﬁed in the next section.

5.2 Anonymity

To protect against the procrastinating attack described

in section 4.2, there must be complete separation be-

tween the registration and bidding stages of an auc-

tion. This means that all bidders must register prior to

the Auctioneer accepting any bids. This is a straight-

forward matter for English, Vickrey and Dutch auc-

tions as the Auctioneer can prevent the auction from

starting until all bidders have registered.

However, in CDAs it is impossible to separate the

registration and bidding stages. In this situation a

group signature scheme can be used. Group signa-

tures are unlinkable, which means that given two sig-

natures, it is impossible to tell if the same user signed

both messages. This thwarts the procrastinating at-

tack as S

can no longer determine if the signature

that they are observing belongs to the newly regis-

tered bidder or someone else. Even if S

does learn

the mapping between the newly registered bidder and

the signature on a bid, the registration manager will

not be able to link future bids to the bidder due to the

unlinkability property of the group signature.

5.3 Bid Authentication

In general, authentication protocols require consider-

able time consuming operations such as exponentia-

tion. However, there are algorithms that can be em-

ployed for performing multiple veriﬁcations in one

stage/operation (e.g., (Bellare et al., 1998)). Group

signatures are also an effective method of performing

bid authentication.

5.4 Price Determination

Bidders must be allowed ﬂexibility when choosing

their bid values. Using a group signature approach fa-

cilitates price ﬂexibility as bidders are free to choose

whatever bid values they desire. Furthermore, a group

signature scheme does not require the use of a dis-

avowal protocol. In general, designers of electronic

auctions should avoid disavowal protocols.

5.5 Payment Enforcement

As stated in Section 4.5, digital cash schemes only

serve as a non-repudiation mechanism in auctions

and makes the scheme conceptually harder to under-

stand. There are more efﬁcient identity escrow mech-

anisms other then digital cash. Again group signature

schemes are an ideal choice. When there is a dispute,

(i.e., someone repudiates a bid, or refuses to pay), the

group manager can reveal the identity of the person

that signed the bid in question. This is more efﬁcient

then a digital cash scheme and serves the same pur-

pose.

5.6 Group Signature Auction Model

This section proposes a generic auction model using a

group signature scheme. The model incorporates the

recommendations from the previous subsections. Fur-

thermore, it gives the designer ﬂexibility to use any

group signature scheme.

There are three parties in the auction:

1. A Bidder, who is interested in submitting bids for

an item offered by a seller.

2. An Auctioneer, who organises the auction, accepts

the bids and determines the winner according to the

auction rules. The Auctioneer also holds the corre-

sponding relation of the identity and a token asso-

ciated with each bidder. The Auctioneer has access

to a publicly veriﬁable bulletin board.

3. A Registrar, who takes part in a protocol in order to

complete the registration of a bidder who has ob-

tained a token from the Auctioneer. At the end of

the protocol, the bidder obtains a secret key that

enables him/her to generate signed bids in a proper

format.

Setup - The Auctioneer organises the auction (i.e., ad-

vertising and calls for auction). The Registrar sets up

the group public key and his secret key.

Registration - A user submits a request to the Auc-

tioneer to participate in the auction. The Auctioneer

veriﬁes the identity of the requestor, and issues a to-

ken that is veriﬁable by the Registrar. The user then

takes part in a protocol with the Registrar, in order

to obtain his secret key and a certiﬁcate of member-

ship in the auction. Note that the token does not carry

the real identity of the bidder, but all communication

between the Registrar and the owner of a token is au-

thenticated, and will be kept for tracing, or revealing

the identity of users associated with tokens.

ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS

346

Bidding - Using a membership certiﬁcate, a bidder

can generate anonymous and unlinkable group signa-

tures on a bid. A bidder submits a bid to the Auc-

tioneer signed using the secret key. The Auctioneer

veriﬁes the signature on the bid using the public key.

If the bid is valid, the Auctioneer posts it on the bul-

letin board.

Winner Determination - The Auctioneer determines

the auction outcome according to auction rules (i.e.,

English, Vickrey, etc.). The auction result is posted on

the bulletin and the winner can produce his/her signed

bid as evidence that they won.

Traceability - In the event of a dispute (i.e., bid

repudiation), the Auctioneer and the Registrar can

combine their information to reveal the identity of a

signer.

6 CONCLUSION

Limited attention has been paid to the design issues

of electronic auctioning schemes. This paper demon-

strated that poor auction designs breach the security

of any auction scheme irrespective of how secure the

underlying cryptographic building blocks are. Auc-

tions were examined in terms of trust, anonymity, bid

authentication, price determination and payment en-

forcement.

We have shown that many schemes proposed in lit-

erature are not practical and can be broken by exploit-

ing weakness in the fundamental design employed. A

group signature scheme can solve many of the prob-

lems in electronic auction design. However, this is not

an all-encompassing solution to all of the design is-

sues. It is insufﬁcient to rely on cryptographic mech-

anisms alone. An auction system is only secure as its

weakest component.

There still remain many pressing issues in design-

ing electronic auctions. Now the time has come for

the designers of auction schemes to step away from

the small-view approach and observe the auction sys-

tem as a whole. Designers need to analyse how each

component interacts and scrutinise whether the cryp-

tographic methods employed are really sufﬁcient for

use in electronic auction schemes.

REFERENCES

G. Ateniese, J. Camenisch, M. Joye, and G. Tsudik,

“A Practical and Provably Secure Coalition-Resistant

Group Siganture Scheme,” in Advances in Cryptol-

ogy - Proceedings of CRYPTO 2000 (M. Bellare,

ed.), vol. 1880 of Lecture Notes in Computer Science,

pp. 255–270, Springer-Verlag, 2000.

M. Bellare, J. Garay, and T. Rabin, “Fast Batch Veriﬁcation

for Modular Exponentiation and Digital Signatures,”

in Advances in Cryptology - Proceedings of EURO-

CRYPT ’98 (K. Nyberg, ed.), vol. 1403 of Lecture

Notes in Computer Science, pp. 236–250, Springer-

Verlag, 1998.

C. Boyd and W. Mao, “Security Issues for Eelctronic Auc-

tions,” tech. rep., Hewlett Packard, TR-HPL-2000,

2000.

F. Brandt, “Fully private auctions in a constant number of

rounds,” in Proceedings of the 7th Annual Conference

on Financial Cryptography (FC) (R. Wright, ed.), vol.

2742 of Lecture Notes in Computer Science, pp. 223–

238. Springer-Verlag, 2003.

C. Cachin, “Efﬁcient Private Bidding and Auctions with an

Oblivious Third Party,” in 6th ACM Conference on

Computer and Communication Security, pp. 120–127,

1999.

M. Franklin and M. Reiter, “The Design and Implementa-

tion of a Secure Auction Service,” IEEE Transactions

on Software Engineering, vol. 22, pp. 302–312, May

1996.

M. Harkavy, J. Tygar, and H. Kikuchi, “Electronic Auctions

with Private Bids,” in the 3rd USENIX Workshop on

Electronic Commerce, Aug. 1998.

H. Kikuchi, M. Harkavy, J. Tygar, “Multi-round Anony-

mous Auction Protocols,” IEEE Workshop on De-

pendable and Real-Time E-Commerce Systems,

pp. 62–69, 1998.

M. Naor, B. Pinkas, and R. Sumner, “Privacy Preserving

Auctions and Mechanism Design,” in The 1st Confer-

ence on Electronic Commerce, pp. 129–139, 1999.

K. Sakurai and S. Miyazaki, “A Bulletin-Board Based Dig-

ital Auction Scheme with Bidding Down Strategy,” in

International Workshop on Cryptographic Techniques

and E-Commerce, pages 180-187, 1999.

J. Trevathan, “Security, Anonymity and Trust in Elec-

tronic Auctions,” Association for Computing Machin-

ery, Crossroads Magazine, Spring Edition, vol. 11.3,

2005.

K. Viswanathan, C. Boyd, and E. Dawson, “A Three Phased

Schema for Sealed Bid Auction System Design,” in

Proceedings of ACISP 2000 –Australasian Confer-

ence on Information Security and Privacy (E. Daw-

son, A.Clark, and C. Boyd, eds.), vol. 1841 of Lecture

Notes in Computer Science, pp. 412–426, Springer-

Verlag (Berlin), 2000.

C. Wang and H. Leung, “Anonymity and Security in Con-

tinuous Double Auctions for Internet Retails Market,”

in the 37

Hawaii International Conference on Sys-

tems Sciences, 2004.

DESIGN ISSUES FOR ELECTRONIC AUCTIONS

347