RELIABILITY EVALUATION OF WDM NETWORKS WITH

LINK CAPACITY AND HOP CONSTRAINTS

Hehong Fan, Mingde Zhang, Xiaohan Sun

Lab of Optical Communications and Photonics, Southeast University, Nanjing, 210096, China

Keywords: network performability, WDM network, link capacity, reliability evaluation, channel-related elements,

multiple working-states object (MWSO)

Abstract: A reliability evaluation module is presented for study of WDM network reliability. In this module, WDM

networks are assumed to consist of three kinds of network elements - nodes, links and wavelength channel-

related elements. And a network performance index – network ‘function value’, was introduced here as a

quantitative representation of working-state of WDM network under certain link capacity and hop

requirements. In addition, WDM networks here are assumed to be a survivable network, which can operate

in a degradative manner against destruction and thus have multiple working-states instead of two opposite

states. The reliability evaluation module was used to analyse the reliability of a WDM network with

CERNET topology. Simulation results indicate that different link capacity requirement as well as different

working-state requirements may lead to different reliability evaluation results, and the differences will

enlarge very quickly with the increasing of network element failure rates. This implies that the study of

WDM network reliability should be performed under multiple working-states assumption and the addition

of the new network element kind - a wavelength channel-related element is necessary.

1 INTRODUCTION

The restoration techniques used in large-scale

network systems make it possible for networks to

survive in a degradative manner against destruction.

Therefore the assumption that network systems have

only two opposite working-states is not justifiable

any more. It was suggested in our former paper (Fan

Hehong et. al, 2005) that large-scale network

systems should be regarded as having multiple

working-states. Such idea has appeared in some

other studies recently, in which large complex

systems like network are deemed as multi-failure-

state systems

(Julia V. Bukowski, William M.

Goble., 2001)

, or having additional working states,

e.g. failure sectioning state

(Enrico Carpaneto et. al,

2002). Thus a network performance index is needed

for the classification of working states. Whereas not

only network connectivity

(Kent Fitzgerald et. al,

2003), (AboElFotoh et. al, 2001) but also network

performance

Ali M. Rushdi (1998). is important for

communication, a composite performance and

reliability measure for network, i.e. performability

(J. F. Meyer, 1980), (B. R. Haverkort, I. G.

Niemegeers, 1992), is worthwhile to examine.

Thereby, an index, function value, representing the

percentage of network meeting certain Qos

requirement is introduced in this paper. For WDM

networks, PLR (packet loss ratio) and delay are two

fundamental Qos indexes and has tight relationship

with link capacity and hop separately. So network

function value are calculated with link capacity and

hop constraints.

Considering that there exist such kind of

elements in WDM network whose failure affect

neither the nodes nor the entire links but certain

wavelength channels in the links, such as

transponders in OLTs (optical line terminals), a new

kind of network element is added to the traditional

elements (nodes and links) of network reliability

evaluation module, namely wavelength channel-

related elements. In this way, links in WDM

network may be up or totally down or only shrink in

capacity. The necessity of this addition is reinforced

by the fact that WDM network protection/restoration

schemes may operate in different layers, such as in

optical multiplex section (OMS) layer, which

restores the entire group of lightpaths on a link, and

the optical channel (OCh) layer, which restores only

one lightpath at a time.

In the following parts, some knowledge for

reliability of multiple working-states object

210

Fan H., Zhang M. and Sun X. (2005).

RELIABILITY EVALUATION OF WDM NETWORKS WITH LINK CAPACITY AND HOP CONSTRAINTS.

In Proceedings of the Second International Conference on e-Business and Telecommunication Networks, pages 210-215

DOI: 10.5220/0001419902100215

 SciTePress

(MWSO) as well as the reliability evaluation module

for WDM networks was introduced in the second

part. Then the algorithm of the network

performability index – function value was described

in the third part for the first time. In the fourth part

the reliability of CERNET (China Education and

Research Network) topology was studied as an

example to demonstrate the use of this module.

Finally, a conclusion will be drawn in the final part.

2 RELIABILITY EVALUATING

OF MWSO

2.1 Network performability index -

network function value

Performability index in different papers may be

different, such as service availability, frame loss

(V.Catania et. al, 1990), network delay and capacity

(Alexander A.Hagin, 1994)

etc. While communication

network systems are used to ensure all the nodes in

the network to normally communicate with each

other, here the performability index - function-value,

, was defined as the percentage of node pairs in the

network that can communicate with each other under

certain performance requirement. And the

performance requirement includes link capacity and

maximum hop of connections. In other words,

network function value represents the degree in

which the network nodes as a whole can accomplish

their required communication tasks.

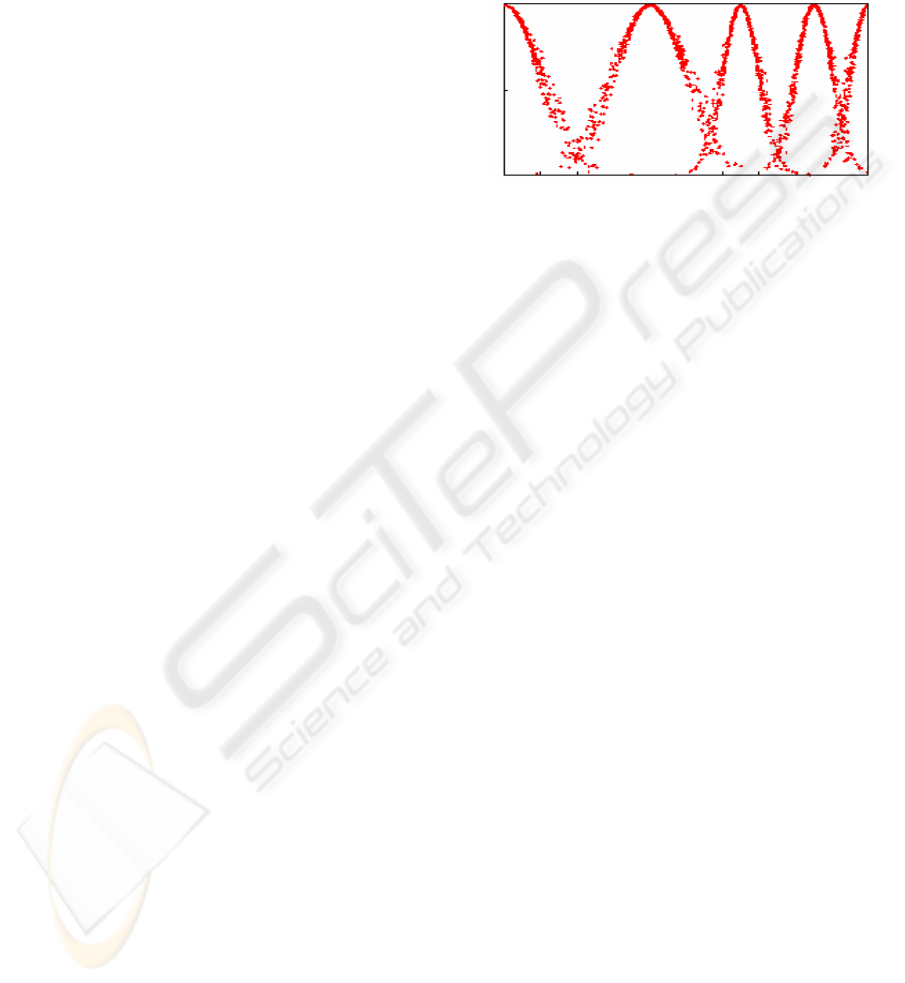
2.2 State term cloud series (STCS)

and reliability of MWSO

Whereas network function value of network can be

regarded as a quantitative representation of network

working states, it’s not necessary for us to study

network reliability according to each function value.

In other words, working states of network can be

classified to several states. As we can always use a

series of linguistic terms, such as “very good”,

“fairly good”, “medium”, “bad”, “worst” and words

alike to describe all kinds of variables, working

states of network can also be classified to several

kinds like this. Relation between the qualitative

description (working state) and the quantitative

description (v

) for working states can be explained

explicitly by Linguistic Cloud Model (LCM) (Huang

Haifeng et. al, 2001), (Li De-yi et. al, 2000). And a

series of linguistic term cloud - state term cloud

series (STCS)

(Fan Hehong et. al, 2005), as showed

in figure 1, demonstrate the qualitative description

of a variable at the full length of its defined value

area with reference to its quantitative values. With

STCS we can scientifically differentiate the multiple

working-states of network easily.

With respect to the reliability of MWSO, the

parameters should be confined by not only stated

conditions and time but also certain state linguistic

term (SLT), w. Reliability of MWSO confined by

term w is:

{

}

( ) | ( ) (1)

wfw

Rt Ptv x b=>−

Here

0,w

refers to the expected value (information

center) of word w, and b refers to the bandwidth of

its membership cloud (fuzziness of the concept).

And the availability of MWSO, A

, in time interval

between t1 and t2, is defined as the time weighted

function value percentage:

,max

( ) / ( 2 1) (2)

bff

Avdtvtt=⋅−

∫

Additionally, for repairable MWSO, useful life

under certain circumstances and repair rate was

defined as the operating time before its availability

of certain period length drops to an unacceptable

value.

2.3 Mapping form WDM network

elements to elements in the

Reliability evaluation module

WDM networks are typically consisting of OXCs

(optical crossconnects), OLTs (optical line

terminals), OADMs (optical add/drop multiplexers),

fibers and sometimes OAs (optical amplifiers)

(Rajiv

Ramaswami, Kumar Sivarajan)

. Furthermore,

transponders and optical multiplexer/demultiplexers

are two fundamental units that make up OLTs and

OADMs of parallel architectures. As transponders

operate on and affect certain wavelength channels in

the link, they may be regarded as the channel-related

elements, which affect only capacity of the related

Figure 1: Diagram of STCS.

0 20 40 60 80 100

worst bad medium good very good

(

)

RELIABILITY EVALUATION OF WDM NETWORKS WITH LINK CAPACITY AND HOP CONSTRAINTS

211

link. While OXCs and multiplexer/demultiplexers in

the OLTs and OADMs always handle all the

wavelength channels in a link together, they can be

considered as composing the nodes in the traditional

network reliability module. Different from OADMs

of parallel architectures, some OADMs are

composed of wavelength selective units in series.

This kind of OADM can be considered as being

composed of node in serial with wavelength

channel-related elements. In addition, the failure of

fibers or fiber bundles and OAs will affect all the

wavelength channels in it at the same time.

To sum up, the mapping from the WDM network

elements to the elements in the reliability evaluation

module can be implemented as follows: each

conjunction node in the topology in backbone WDM

networks, either OADM or made up of OXC and

OLTs, can be deemed as composed of a node and

channel-related elements in series; Fibers (or fiber

bundles) and sometimes OAs consist the network

links.

2.4 Reliability evaluation module for

WDM network

Based on the reliability information of the nodes,

links and channel-related elements (mainly

transponders), reliability of WDM networks can be

figured out by way of Mont Carlo simulation. The

main steps to evaluate the reliability of networks are

listed as follows:

1). Make use of the failure distribution function

knowledge of the elements, by way of Mont Carlo

method, to simulate function value, v

, under certain

link capacity and maximum connection hops

requirement, and A

of certain period length of the

network system (by Eq. (2)) changing over time.

2). Repeat step 1 to obtain the distribution of the

system’s v

and A

at different time as well as

average short period A

and useful life distribution,

confined by certain capacity and hop requirement

and SLT of STCS.

3). Reliability confined by a SLT at t can be

calculated by Eq. (1).

4). SLT to describe the system’s running state and

reliability level can be determined according to

STCS.

3 ARITHMETIC OF NETWORK

FUNCTION VALUE

Different from some former methods (K. K.

Aggarwal, 1998) which begin with the minimum

sets to calculate network capacity, we’ll begin with

the weighted adjacency matrix A=[a

]

, working-

state vector of nodes B=[b

…b

] and working-

state matrix of channel-related elements C=[c

]

the network to calculate the function value, v

, of the

network. Here, the element a

in A represent the

maximum capacity of the link directs from node i to

node j. If there isn’t a direct edge connects from

node i to node j, the link capacity from link i to link j

is regarded as 0. So the total link number is the

number of non-zero elements in A. b

(0 or 1) in B

indicates whether the node i is up or down. c

in C

refers to the channel j in link i. The total number of

node and link are separately m and n while the

maximum number of channel in each link is k. In

this method we don’t want to calculate the minimum

sets as even the minimum path may have more hops

than required.

Whereas undigraph can be transferred to digraph

easily by replacing each directionless link with a

couple of directional links in opposite direction, only

the algorithm for digraph is given below:

Step 1: For each link i, calculate the available

capacity, that is, to subtract the number of failure

channels,

∑

in it from the maximum capacity.

Step 2: current adjacency matrix,

=[ ]

ccij

Aa, can be

reckoned by delete (or set zeros) columns and arrays

in A according to the zeros in B.

Step 3: calculate the reachable matrix, R, under

certain capacity requirement for the links within h

hops of the remaining adjacency matrix, A

The reachable matrix of l hops,

() ()

=[ ]

ccij

Aa, can

be obtained from the reachable matrix of l-1 hops,

(1) (1)

=[ ]

ccij

−−

, by

Figure 2: A WDM wavelength-routing network

ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS

212

(

)

(

)

(

)

(

)

cc1c1cc

max(min( , ),...,min( , )) 3

ll l

ij i j im mj

aaaaa

−−

Thus reachable matrix R can be work out by

()

(

)

cc c

max( , ,..., ) (4)

ij ij ij ij

raaa=

As any nodes in the network are not required to

communicate with themselves, the diagonal of R is

set to be zero for further calculation.

Setp4: Two kinds of v

f,system

are defined and used

here. One kind is a normal one which is the amount

of elements in R that are no less than the required

capacity; and the other is a normalized one which

denotes the percentage of maximum minimum link

capacity of all the routes between node pairs in the

network with reference to maximum minimum link

capacity of all the routes between node pairs in the

failure-free network:

()

/ ( 1) 5

fsystem

vrmmk=×−×

∑

It can be easily figured out that the maximum

traditional function value and maximum normalized

function value of an m-node WDM network with k

channels in each link are separately

(1)mm×−

and 1.

4 APPLICATION OF THE

EVALUATION MODULE

0 1

300

1300

1000

1300

500

1300

1600

1300 1350

900

1000

650

Figure 3: topology of 10-node CERNET

To demonstrate the reliability evaluation module,

WDM network of CERNET topology is used here as

an example. The elements are supposed to follow

Weibull failure distribution in order to examine the

system reliability parameters changing with failure

rates rising. Figure 2 showed the topology of

CERNET, and the nodes in the topology, either

made up of OXC or OADM, are all assumed to

consist of node and 2x16 parallel channel-related

elements in series with connected link. The shape

parameters and location parameters of the elements

are assumed to be 3 and 0 separately. And the scale

parameters of nodes, channel-related elements

(transponders) and links are assumed to be 20000h,

50000h and 50000h, respectively. As operation of

the nodes in the WDM networks need power supply,

the reliability of such equipment is considered to be

much lower than the passive element – fiber link. In

addition, while nodes in WDM networks are larger

and more complexly configured than transponder,

scale parameters of transponders are also deemed as

larger than those of nodes. MTTR here is assumed to

be 2h. The simulation is repeated 100 times and the

time step is 96h (4 days). Every node is assumed to

have full wavelength conversion capability, so that

traffic in some failed wavelength channels can be

restored in other working or backup channels. The

maximum hops between each node pairs are limited

to 4.

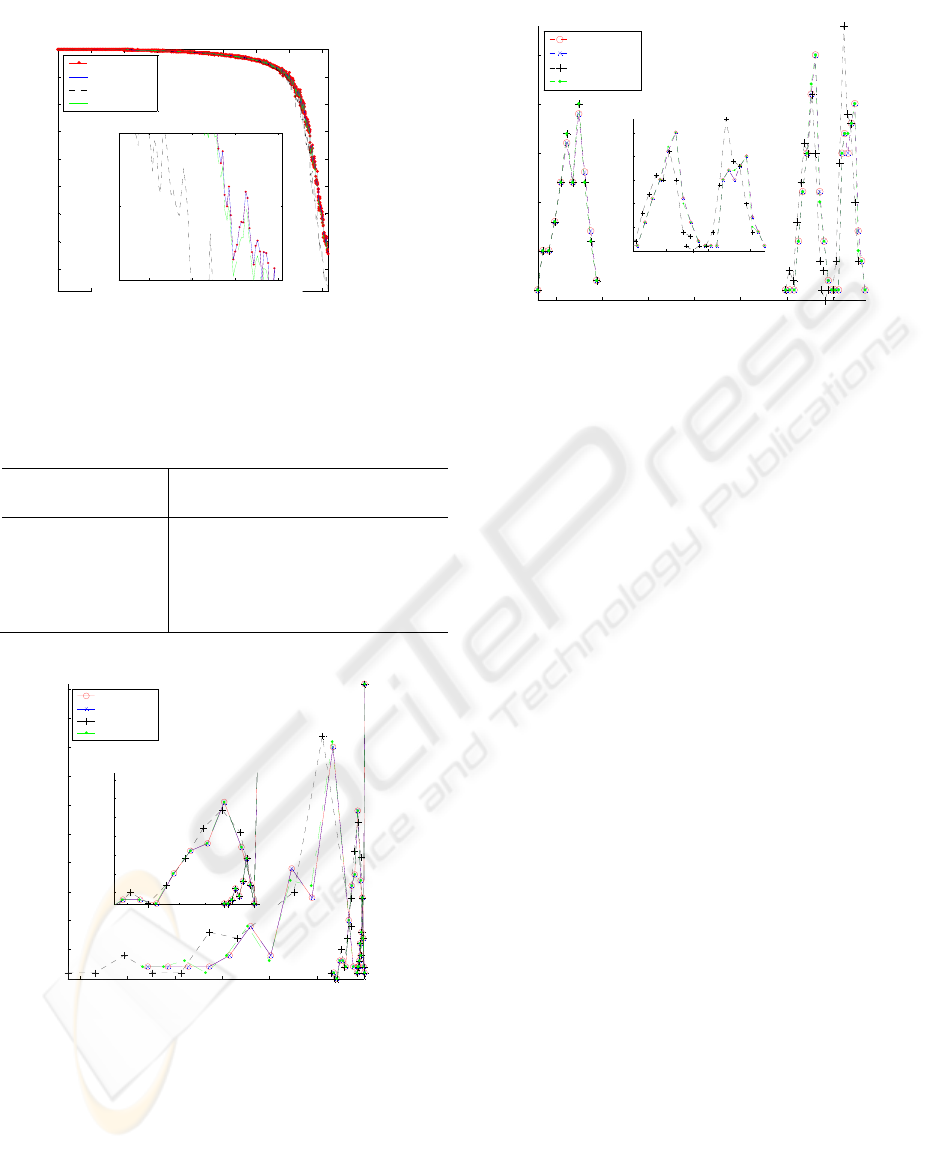
The simulation results are showed in the

following three figures. Fig (4) shows that while

there is no perceptible difference between average

availability between different link capacity demands

when failure rates are rather low, the network

availability under full channel requirements (16

channels) are lower than availability of all the other

three conditions, and the distance between them

become more and more larger with failure rates went

higher. This is further proved by the figures listed in

table 1, during which there is no difference between

different capacity requirement at 47904h, and only

0.0002 in difference between capacity requirement

of 16 channels and that of the other three at 95904h,

while the difference arise to about 0.025 after

another 47904h and finally reached 0.13 at 163104h;

the slightly lower value of normalized availability

than the availability under two lower channel

number demands, and the same value of availability

under 8 and 1 channel demands indicate that such

kind of channel demand may be easy to meet and

there’re very little chance for only a few channels

left under the element failure distribution

assumptions given above.

RELIABILITY EVALUATION OF WDM NETWORKS WITH LINK CAPACITY AND HOP CONSTRAINTS

213

2 4 6 8 10 12 14 16

x 10

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1 channel

8 channels

16channels

normalized

Figure 4: Average CERNET availability of 96h under

different link capacity requirements changing with

working time (and failure rates)

Table 1: Average CERNET availability of 96h under

different link capacity requirements at four different

working time (denote different failure rates)

Working time(h)

Capacity demand

47904 95904 143904 163104

normalized

0.9969 0.9802 0.8573 0.2550

0.9969 0.9800 0.8317 0.1199

0.9969 0.9802 0.8556 0.2441

0.4 0.5 0.6 0.7 0.8 0.9 1

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

1 channel

8 channels

16channels

normalized

Figure 5: CERNET availability distribution of 96h

changing with working time and failure rates. The three

groups of lines from left to right are separately at working

time of 47904h, 95904h and 143904h.

Figure 5 told us that when failure rates are rather

low, the short period availability concentrated near

1, but as failure rates going up, the distribution of

availability becomes widen, from 0.01 at 47904h, to

0.05 at 95904h, to about 0.6 at 143904h, which

implies that the system begun to be unstable.

2 4 6 8 10 12 14

x 10

0.05

0.1

0.15

0.2

0.25

1 channel

8 channels

16channels

normalized

Figure 6: distribution of CERNET useful life under

different capacity and SLT requirements. Performance

requirement SLTs of the line groups from left to right be

separately “perfect”, “very good” and “good”.

From figure 6 we can see that useful life become

longer and longer with SLT of network performance

become lower. What is more important is that

although the distance of availability requirement

between “perfect” (expected value is 1 and

bandwidth 0) and “very good” (expected value is 1

and bandwidth 0.05) are very small, their useful life

are far cry from similar: the average useful life of

“very good” performance requirement are almost 5

times the length of “perfect”, separately 1.30х105h

and 0.26х105h. Which have a sharp contrast with it

is that, although the distance of availability

requirement between “good” (expected at 0.85) and

“very good” are much larger than the former two,

useful life of them hasn’t that big difference. These

results show that while reliability level and useful

life increases with performability requirement

decrease, the extent that useful life increases are not

proportional to the decrease of performability

requirement. Only a very small step down from the

requirement of “perfect” will lead to a great longer

useful life but further decrease of performability

requirement will have much lower effect on

lengthening useful life.

5 CONCLUSION

Simulation results indicated that different link

capacity requirement for network may lead to

different evaluation results, especially when failure

rates are high and the differences enlarge very fast

with the increasing of failure rate; different working-

state requirements may lead to fairly different

reliability evaluation results as well: the lower the

0.95 0.96 0.97 0.98 0.99

0.05

0.1

0.15

0.2

0.25

0.3

0.35

1.54 1.56 1.58 1.6

x10

0.4

0.45

0.5

1.3 1.4 1.5

x 10

0.05

0.1

0.15

0.2

0.25

ICETE 2005 - SECURITY AND RELIABILITY IN INFORMATION SYSTEMS AND NETWORKS

214

performability requirement the higher the reliability

level, and the lengthening of useful life are not

proportional to the decrease of performability

requirement - a small step down from the

requirement of “perfect” (to “very good”) will be

enough to lengthen the network useful life

remarkably.

All these results imply that study of network

reliability should be performed under multiple

working-states assumption and the addition of the

new network element kind - wavelength channel-

related elements for reliability analysis of WDM

network is necessary.

REFERENCES

Fan Hehong, Sun Xiaohan, Zhang Mingde (2002). A novel

fuzzy evaluation method to evaluate the reliability of

FIN. Retrieved January, 2005, from Southeast

University, Library Web site:

http://www.lib.seu.edu.cn/database/disp.asp?info_id=4

Julia V. Bukowski, William M. Goble. (2001). Defining

Mean Time-to-Failure in a Particular Failure-State for

Multi-Failure-State Systems. Retrieved January, 2003,

from Southeast University, Library Web site:

http://www.lib.seu.edu.cn/database/disp.asp?info_id=4

Enrico Carpaneto, Alessandra Mosso, Andrea Ponta,

Emiliano Roggero (2002). Comparison of Reliability

and Availability Evaluation Techniques for distribution

Network Systems. Proceedings of RAMS, 563-568.

Kent Fitzgerald, Shahram Latifi, Pradip K. Srimani

(2002). Reliability Modeling and Assessment of the

Star-Graph Networks. Retrieved March, 2003, from

Southeast University, Library Web site:

http://www.lib.seu.edu.cn/database/disp.asp?info_id=4

Manzi E., Labbe M., Latouche G.., Maffioli F. (2001).

Fishman's sampling plan for computing network

reliability. Retrieved March, 2003, from Southeast

University, Library Web site:

http://www.lib.seu.edu.cn/database/disp.asp?info_id=4

AboElFotoh, H.M.F., Al-Sumait, L.S. (2001). A neural

approach to topological optimization of

communication networks with reliability constraints.

Retrieved March, 2003, from Southeast University,

Library Web site:

http://www.lib.seu.edu.cn/database/disp.asp?info_id=4

V.Catania, A. Puliafito, L. Vita (1990). Availability and

performability assessment in LAN interconnection.

Retrieved March, 2002, from Southeast University,

Library Web site:

http://www.lib.seu.edu.cn/database/disp.asp?info_id=4

Alexander A.Hagin (1994). Performability, reliability, and

survivability of communication networks: system of

methods and models for evaluation. Retrieved March,

2002, from Southeast University, Library Web site:

http://www.lib.seu.edu.cn

K. K. Aggarwal (1998). A fast algorithm for the

performance index of a telecommunication network.

Retrieved March, 2002, from Southeast University,

Library Web site:

http://www.lib.seu.edu.cn/database/disp.asp?info_id=4

Ali M. Rushdi (1998). Performance indexes of a

telecommunication network. Retrieved March, 2002,

from Southeast University, Library Web site:

http://www.lib.seu.edu.cn/database/disp.asp?info_id=4

J. F. Meyer (1980). On evaluating performabiity of

degradable computing systems. IEEE Trans. Comput.,

C-29, 720-731.

B. R. Haverkort, I. G. Niemegeers (1992). A

performability modelling tool based on the dynamic

queueing network concept. Retrieved 2002, from

Southeast University, Library Web site:

http://www.lib.seu.edu.cn

Huang Haifeng, Sun Xiaohan, Dai Wen, Zhang Mingde

(2001). Reliability analysis based on membership

cloud model in Distributed Optical fiber Industrial

network. Retrieved January, 2005, from Southeast

University, Library Web site:

http://www.lib.seu.edu.cn

Li De-yi, Di Kai-chang, Li De-ren, Shi Xue-mei (2000).

Mining Association Rules with Linguistic Cloud

Models. Retrieved March, 2001, from Southeast

University, Library Web site: http://

http://www.lib.seu.edu.cn/database/disp.asp?info_id=1

Rajiv Ramaswami, Kumar Sivarajan, Optical Networks: A

Practical Perspective. Morgan Kaufmann Publishers,

2nd edition.

RELIABILITY EVALUATION OF WDM NETWORKS WITH LINK CAPACITY AND HOP CONSTRAINTS

215