Generalizing e-Bay.NET: An Approach to
Recommendation Based on Probabilistic Computing
Luis M. de Campos, Juan M. Fern
´
andez-Luna and Juan F. Huete
Departamento de Ciencias de la Computaci
´
on e Inteligencia Artificial
E.T.S.I. Inform
´
atica, Universidad de Granada, 18071 – Granada, Spain
Abstract. In this paper, we shall present the theoretical developments related to
extending existing e-Bay.NET recommendation system in order to improve its ex-
pressiveness. In particular, we shall make them more flexible and more general
by enabling it to handle evidence items with a finer granularity so that more accu-
rate information may be obtained when user preferences are elicited. The model
is based on the formalism of Bayesian networks, and this extension requires the
design of new methods to estimate conditional probability distributions and also
a new algorithm to compute the posterior probabilities of relevance.
1 Introduction
Content-based recommendation systems (RS) [9] attempt to recommend items based
exclusively on user preferences. In a basic e-commerce application, information about
users’ tastes and preferences are either collected explicitly (using a form or question-
naire when they log in) or implicitly (using purchase records, viewing or rating items,
visiting links, taking into account membership to a certain group, etc.). All the user
information stored by the RS is known as the user profile. The main characteristic of
RSs is that not only do they return the requested information, but they also attempt to
anticipate user needs.
In [7], a probabilistic computing-based RS (e-Bay.NET) was presented. This is
a recommendation system that can be used in e-commerce applications and which is
based on Bayesian Network formalism, or ”e-buying” in the Web NETwork. By using
Bayesian networks (BN) (one of the two major paradigms of probabilistic reasoning),
we can combine a qualitative representation of the problem (which explicitly repre-
sents the dependence and independence relationships between those products, articles
or items to be recommended and the user profile) with a quantitative representation by
means of a set of probability distributions, measuring the strength of these relationships.
Given the user profile which contains user preferences about a given item, the system
recommends the most relevant products in terms of user needs, which are ranked ac-
cording to their a posteriori probability of relevance.
In order to recommend a product, our system shall take two different (but com-
plementary) situations into account which describe the product’s ability to match user
needs: firstly, the exhaustivity of the product models the extent to which the product
contains all the features required by the user; and secondly, the specificity of the prod-
uct measures the extent to which all the user needs match the product. A product might
M. de Campos L., M. Fernández-Luna J. and F. Huete J. (2005).
Generalizing e-Bay.NET: An Approach to Recommendation Based on Probabilistic Computing.
In Proceedings of the 1st International Workshop on Web Personalisation, Recommender Systems and Intelligent User Interfaces, pages 24-33
DOI: 10.5220/0001423000240033
Copyright
c
 SciTePress

therefore be exhaustive but not specific (all the product features are included in the user
preferences, but the user profile contains more preferences which are not included in
the product) and vice versa (all the features in the user profile belong to the product,
but the product is also described with many other features). The final decision will be a
combination of these two dimensions.
In this paper, we shall extend the features of e-Bay.NET, particularly those relating
to products and user need descriptions, and this involves modifying the quantitative
component of the system. e-Bay.NET [7] therefore only considers bivaluated evidence
items, i.e. each product is represented by a list of items or features which describe
it, and users express their preferences with only two alternatives: the item matches or
does not match their preferences. The purpose of this paper is to enable the system
to handle evidence items with a finer granularity in order to obtain finer information
when user preferences are elicited. In order to fulfill this objective, we must redefine
how the probability distribution is computed for each node in the Bayesian network and
reformulate the original propagation algorithm that computes the posterior probability
of relevance of each product given a user profile.
Although many other approaches to RS have been published [1,9], probabilistic
graphical models have been used in this field in different areas: BN learning algorithms
are the tools with which the user profile is built [13, 11, 14, 4]; BN-based classifiers have
also been employed in collaborative filtering [2, 10, 12]. In addition, influence diagrams
[8] have been used to deal with RS, presenting the problem as a decision task. Focusing
as it did on hierarchical domains (i.e. the items to be recommended can be grouped in a
hierarchy), this approach was considered in [6]. In this case, the model makes decisions
about which items in the hierarchy are more useful to the user.
The paper is structured in the following way: Section 2 briefly describes the e-
Bay.NET topology; Section 3 explains the new semantic for feature variables; Section
4 describes how to estimate the probability distributions that measure the strength of
the relationships; Section 5 examines how inference is carried out in order to give rec-
ommendations to the user on the application domain; Section 6 presents an example
illustrating the model; and finally, Section 7 discusses the conclusions and future lines
of research.
2 e-Bay.NET Recommendation System
Firstly, we shall briefly describe the different kinds of nodes in the underlying BN and
how they are related to each other. Figure 1 shows the proposed BN topology where,
in order to model the problem, five different sets of variables (nodes in the graph) have
been considered: feature nodes, F, which represent product features and are also the
items by which users can express their preferences; exhaustivity nodes, E, which are
used to model whether the product does or does not describe user preferences; speci-
ficity nodes, S, which are used to represent the specificity of a product to the user
profile; advisable nodes, A, which represent the final decision (i.e. whether the prod-
uct is recommended or not to the user); user profile node, U, which is a virtual node
used to represent user preferences.
25

F1 F2 F3 F4 F5
E1
F6
S1
A1
A2
U
E2 S2
Fig.1. e-Bay.NET Recommendation System.
In order to complete the BN, we must specify its topology (the arcs). In this case,
two logical implications must be represented.
i) The first set comprises the relationships which do not change over time and which
are therefore fixed in the system. These relationships are represented with solid
lines in Figure 1. Since a product is described with a fixed set of features, there
is therefore an arc from each feature node to each exhaustivity node representing
the product. With these arcs, we are expressing the fact that the exhaustivity of the
product will depend on the relevance values of the different features that comprise
it
1
. A different set of fixed relationships is used to determine whether a product
is finally recommended or not. In this case, since the final decision will depend on
both exhaustivity and specificity, for each product, we add two arcs which go from
the exhaustivity and the specificity nodes to the advisable node that represents the
product.
ii) The second set of implications is related to those relationships that depend on the
particular user preferences which are represented in the user profile. These rela-
tionships cannot be assessed until the preferences are known, and cannot therefore
be fixed a priori. These relationships are represented by dashed lines in Figure 1.
In these case, we include an arc from the user profile node to each feature used to
represent the user preferences. In addition, and in order to measure the specificity
of the i
th
product, we include an arc from a feature node to the specificity node S
i
whenever the feature belongs to the profile but has not been used to describe the
product.
The model is completed after assessment of the conditional probabilities for each
variable X
i
, P (X
i
| pa(X
i
)), with pa(X
i
) being a configuration for the variables in
the parent set of X
i
, P a(X
i
).
1
Although the topology presented implies that one feature F is marginally independent of any
other feature, this assumption (which is restrictive in some domains) could be relaxed to in-
clude relationships between evidence items [5].
26

3 Enlarging Products and User Profile Description
Since e-Bay.NET only considers bivaluated evidence items, a product is described by
means of a list of keywords matching each of its features. For instance, let us suppose
that a set of movies are the products to be recommended. In this case, the set of fea-
ture keywords used to describe the film Schindler’s list might be: concentration camp,
ghetto, Holocaust, Polish, rescue, survivor, war, Jewish, German, and Nazi. In addition,
and in order to express interest in a feature, users have two alternatives: either the item
matches or it does not match their preferences, although they can express a belief in
each feature in the profile by assigning a weight λ, with 0 ≤ λ ≤ 1, to the feature. For
instance, a user might believe that the movie he is looking for has a 0.7 probability of
being located in Poland (p(location=Poland |user needs ) = 0.7 and p(location=Not
Poland |user needs ) = 0.3), and that its subject matter is the Nazi Holocaust with a
probability of 1 (p(theme=Holoc. |user needs ) = 1.0 and p(theme=Not Holoc. |user
needs ) = 0.0).
In this paper, our objective is to enable the system to handle evidence items with
a finer granularity. With this approach, we are closer to real situations where the de-
scription of a product feature is very often not crisp. For example, we would describe a
movie by indicating that it has a high, medium or low level of romance or, in a different
domain, when describing a car we should distinguish between sports, small cars, vans,
etc.. Although in both cases, the variables RomanceLevel and CarType are associated
to domains that might be described with different values, there is some difference be-
tween them. On one hand, the set of labels used to define the variable RomanceLevel
are ordered (low < medium < high). If we classify a movie as having a high level of
romance, we are therefore also quite confident that “the level of romance in the movie is
medium” and less confident that “the movie has a low level of romance”. On the other
hand, the values taken by the variable CarType are mutually exclusive in the sense that
if a car is described as a small car it will not be described, as a van or a sports car.
Regarding the user profile, it will also be also described by means of multi-labeled
variables. For example, users can express their preferences for a movie about the Nazi
Holocaust but with a low component of comedy by considering that p(theme=Holoc.
|user needs ) = 1.0 and p (theme=Not Holoc. |user needs ) = 0.0 and that p(comedy=low
|user needs ) = 0.8, p(comedy=medium |user needs ) = 0.2 and p(comedy=high |user
needs ) = 0.0. In order to facilitate system interaction, users should also express their
preferences by means of a product list, such as “Schindler’s list” and “The Pianist”,
expressing interest in products (movies) which are similar to the ones given.
Although this generalization has no effect on the topology of the model, it does
have certain implications for the estimation of the probability distributions (see Section
4) and also for the inference process where the propagation algorithm must be reformu-
lated (see Section 5).
4 Estimating Probability Distributions
For each variable X
i
, we must estimate a family of conditional probability distributions
P (X
i
| pa(X
i
)), with pa(X
i
) being a configuration for the variables in the parent set
27

of X
i
, P a(X
i
). These probabilities will be estimated from both the database describing
the products (in the case of the fixed relationships in the BN) and the user profile (in the
case of non-fixed relationships).
Before discussing how to estimate the conditional probabilities, we shall present
some notation: a feature F
j
takes v
j
different values (labels). Given a dataset D, let D
i
be the data record describing the i
th
product and m
i
be the number of features used
to describe D
i
, i.e. D
i
= {f
l
s
,1
, f
l
r
,2
, ..., f
l
t
,m
i
} where f
l,j
represents the fact that the
feature F
j
of the product takes the l
th
-value, 1 ≤ j ≤ v
j
. Let N be the number of
products in the data set and let n
l,j
be the number of times that the l
th
value of feature
F
j
has been used to describe a product in D and let n
•,j
be the number of times that
feature F
j
is used to describe a product in D. In order to measure the importance of a
feature F
j
in the whole data set, we shall use the concept of inverted feature frequency
2
,
iff
j
, defined as
iff
j
= log((N/n
•,j
) + 1)/log(N + 1). (1)
Finally, given a product D
i
, we can define M(D
i
) =
P
F
j
∈D
i
iff
j
.
Below, we shall present guidelines for estimating the conditional probability distri-
butions, beginning with the upper nodes in the graph:
• For every feature F
j
which is a “root” node (it does not belong to the profile U),
we need to assess the a priori probability of relevance for each value l, 1 ≤ l ≤ v
j
,
i.e. p(f
l,j
). In this paper, we propose that the following values be used (although
different alternatives might be considered):
p(f
l,j
) = n
l,j
/N (2)
• Evidence features, i.e. feature nodes used to describe user needs. Since users might
use two different alternatives to express their preferences about a feature F
j
(ex-
plicitly using F
j
in the profile or by means of a set of products containing F
j
), it be-
comes necessary to combine all this information in order to determine the strength
of the feature, p(F
j
|U).
In this paper, we propose that whenever a user explicitly expresses interest in a
feature F
i
(by means of a set of λ
l
values, with 0 ≤ λ
l
≤ 1 and
P
v
j
l=1
λ
l
= 1), the
probabilities will be defined as:
p(f
l,j
|u) = λ
l
, 1 ≤ l ≤ v
j
. (3)
In addition, the feature F
j
only receives evidences since it belongs to certain prod-
ucts in the profile. Let N
j,u
be the number of products in the profile which are
described with feature F
j
and let n(f
l,j
, u) be the number of times that the l
th
value of feature F
j
has been used to describe a product in the profile. In this case,
we propose the use of
p(f
l,j
|u) = n(f
l,j
, u)/N
j,u
. (4)
2
The inverted feature frequency has the same role as the inverted document frequency in the
field of information retrieval [3].
28

• Exhaustivity nodes: in this case, each node E
i
has a binary variable associated
which takes its values from the set {e
−
i
, e
+
i
}, representing the fact that the node ei-
ther does not describe or describes exhaustively the user preferences, respectively.
The assessment of the conditional probabilities, i.e. p(e
+
i
|pa(E
i
)), ∀E
i
∈ E might
be quite difficult (and also its storage) because its size is exponential with the num-
ber of parents of E
i
(features used to describe the product). We therefore propose
modifying the canonical model used in [7] to handle multi-labeled variables, i.e.
p(e
+
i
|pa(E
i
)) =
m
E
i
X
j=1
w(f
l,j
, E
i
). (5)
where l is the value that feature F
j
takes in the configuration pa(E
i
), and w(f
l,j,
, E
i
)
are weights measuring how this l
th
value of feature F
j
describes the product, with
w(f
l,j
, E
i
) ≥ 0 and
P
F
j
∈P a(E
i
)
max
l
w(f
l,j
, E
i
) ≤ 1. Therefore, the more rel-
evant the l
th
value of feature F
j
to E
i
, the greater the probability of relevance of
E
i
.
These weights will be estimated from the dataset D and their definition will depend
on the characteristic of feature F
j
:
1. F
j
is described with a set of mutually exclusive labels: in this case, when a
product D
i
is described by means of the l
th
value of feature F
j
, we exclude the
possibility that this product could be described using a different label. It should
be noted that this situation subsumed the binary case. We therefore propose
using:
w(f
l,j
, E
i
) = iff
j
/M(E
i
) if f
l,j
∈ D
i
w(f
l,j
, E
i
) = 0 Otherwise.
(6)
2. F
j
is described with a set of ordered labels. In this case, when a label l
k
is
used to describe the feature F
k
of a product, we cannot completely discard the
capability of the other l
s
alternatives, with l
s
6= l
k
, to describe the product.
We should therefore estimate the weights by measuring how label l
s
of feature
F
j
describes product D
i
. In order to achieve this objective, we propose the
following:
w(f
l,j
, E
i
) = [1 − Distance(d(j , i), f
l,j
)] ∗ if f
j
/M(E
i
)]
(7)
where d(j, i) is the label used to describe the j
th
feature of product D
i
in the
dataset D and Distance(x, y) is a function that measures how far two labels are
in their domain so that 0 ≤Distance(x, y) ≤ 1 and Distance(x, y) = 0 if x and
y are the same label and increase with their distance in the ranking.
• Specificity nodes: these nodes are used to represent the specificity of a product to
the user profile. Each node S
i
will therefore take its values from the set {s
−
i
, s
+
i
},
representing whether the user profile does not concern or concerns the product,
respectively. Since the parent set of S
i
comprises those features F
j
which have not
been used to describe the i
th
product, a specificity node might have a great number
29

of parents, and therefore the canonical model defined in Equation 5 will be used.
p(s
−
i
|pa(S
i
)) =
m
S
i
X
j=1
w(f
l,j
, S
i
). (8)
In this case, since product D
i
has not been described with feature F
j
, the weights
w(f
l,j
, S
i
) should be defined as w(f
l,j
, S
i
) = if f
j
/M(E
i
). As a consecuence,
the greater number of feautures in the profile which have not been used to describe
product D
i
the greater p(s
−
i
|pa(S
i
)). Recall that p(s
+
i
|pa(S
i
)) = 1−p(s
−
i
|pa(S
i
)).
• For every advisable node, A
i
, p(a
+
i
|E
i
, S
i
) measures the strength of the exhaustiv-
ity and the specificity of the product in the final recommendation. This estimation
is simple since the recommendation node A
i
has only two parents, E
i
and S
i
, and
should be computed by means of:
p(a
+
i
|e
+
i
, s
+
i
) = 1, p(a
+
i
|e
+
i
, s
−
i
) = β
i
, p(a
+
i
|e
−
i
, s
+
i
) = 0, p(a
+
i
|e
−
i
, s
−
i
) = 0
(9)
with 0 ≤ β
i
≤ 1 so the lower β
i
is, the more importance we shall be giving to the
specificity node.
5 Inference
In order to provide the user with an ordered list of recommendations, we must be able to
compute the posterior probability of being recommended for every product, i.e. ∀A
i
∈
A, p(a
+
i
|u) where u stands for the corresponding configuration of the features in the
user profile U. For the computation of these values,
p(a
+
i
|u) =
X
e
i
∈E,s
i
∈S
p(a
+
i
|e
i
, s
i
, u)p(e
i
, s
i
|u).
Considering that firstly, advisable nodes, A
i
, and the user profile node, U, are in-
dependent and given that we know the values of the exhaustivity and specificity nodes,
i.e. p(A
i
|E
i
, S
i
, u) = p(A
i
|E
i
, S
i
), and secondly, for a given product, A
i
, the model
verifies that the variables E
i
and S
i
are conditionally independent given the query, i.e.
p(E
i
, S
i
|u) = p(E
i
|u)p(S
i
|u), then
p(a
+
i
|u) =
X
e
i
∈E,s
i
∈S
p(a
+
i
|e
i
, s
i
)p(e
i
|u)p(s
i
|u).
Taking the values used to define p(A
i
|E
i
, S
i
) in Equation 9, the final probability of
recommending an advisable node is therefore:
p(a
+
i
|u) = p(e
+
i
|u)[β
i
+ (1 − β
i
)p(s
+
i
|u)]. (10)
In order to recommend a product, we need to know values p(e
+
i
|u) and p(s
+
i
|u).
The following theorem (the proof is omitted due to lack of space) shows the conditions
under which these values can be computed efficiently.
30

Theorem 1: Given a user profile, U, and let E
i
and S
i
be the exhaustivity and specificity
nodes, respectively, whose conditional probability distributions can be expressed under
the conditions given by equations 5 and 8, then the exact a posteriori probabilites can
be computed by means of the following formulas, where if F
j
does not belong to profile
u, p(F
j
|u) = p(F
j
):
p(e
+
i
| u) =
m
E
i
X
j=1
v
j
X
k=1
w(f
l
k
,j
, E
i
) · p(f
l
k
,j
| u).
p(s
+
i
| u) = 1 −
m
S
i
X
j=1
v
j
X
k=1
w(f
l
k
,j
, S
i
) · p(f
l
k
,j
| u).
6 Experimental Results
To validate experimentally the proposed model we consider a set of 30 features, F =
{F
1
, . . . , F
30
}, with the first 24 taking their values in an ordered-label domain ({ Very
High (VH)> High (H) > Medium (M) > Low (L) > Very Low (VL) }) and the last
6 features taking their values in a mutually-exclusive domain {l
1
, l
2
, l
3
}. Then, a syn-
thetic data set with 300 products has been obtained by selecting randomly a mean of 14
features for each product.
In order to obtain the test profile, U, we manipulate the product descriptions using
three different criteria: (1) Removal of features belonging to the product; (2) Addition
of attributes that does not belongs to the product; (3) Modification of the label-value of
some features in the original product description.
Using each record in the test profile as input, the system performance is considered
as the ratio between the number of times that the original product is recommended as
first option to the user and the total number of products
3
. Figure 2 displays a selection
of results
4
, sufficient to show the differences in the behavior of the system in the studied
situations. In X-axis we display the different values for the parameter β (see eq. 9) and
in the Y-axis, the system performance is showed. In Figure 2 we indicate by xR, yA and
zM that the test profile has been obtained by manipulating randomly x, y and z features
(removed, added or modified, respectively) in the original data set.
From the experimental outcomes, the first conclusion is that the system has a quite
robust behaviour. Thus, in general, if we manipulate less than a half of the features
describing a product, the system recommends the correct product in all the cases. Fo-
cusing in graph (i) in Figure 2, we can conclude that when the profile contains only a
proper subset of the features describing the product, even using different labels, it is
better to consider the specificity criterion (β = 0.0). The situation changes when new
features are added to the profile (see graphs (ii) and (iii)
5
). In this case it is better to
weak the weight assigned to the specificity (by assessing greater values of β). Thus,
3
We have also used different performance measures, obtaining a similar behaviour.
4
Note that we do not show those results where the system performs properly.
5
The case in which only new features are added to the profile is not displayed because the
exhaustivity is always 1 (p(e
+
|u) = 1).
31

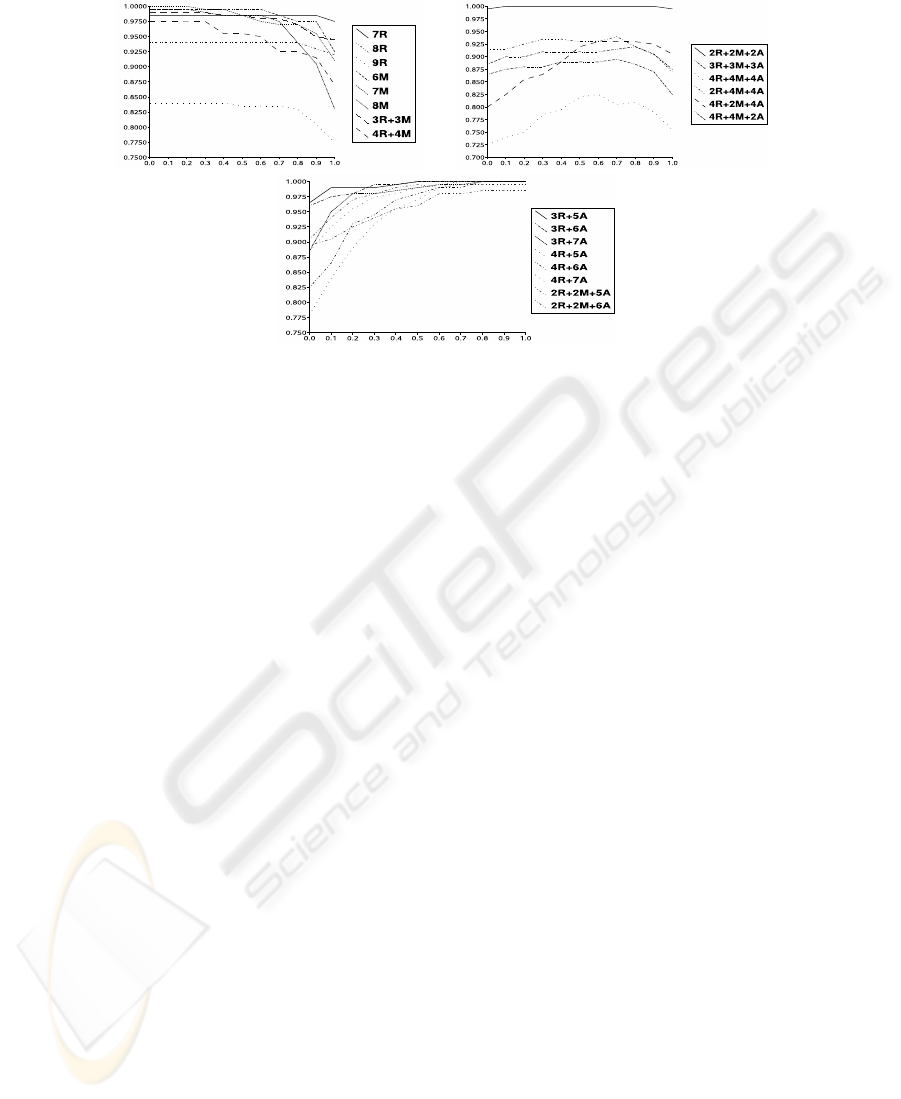
(i) (ii)
(iii)
Fig.2. Experimental results with e-Bay.Net
graph (ii) displays the results obtained with test profiles with a mixture of the different
manipulations, representing, for instance, the query of a non-expert user. In this case,
the optimal values have been obtained with β belonging to the interval [0.6, 0.8]. Fi-
nally, when the number of added features increases (the profile has more “noise”) it is
preferable not to consider the specificity criteria (β = 1) (see graph (iii)). Summing up,
we can conclude with the following rule: “the greater the confidence that we have in
the profile, the greater weights (lower beta values) should be given to the specificity
criterion”.
7 Conclusions
This paper proposes a generalization of a BN-based model for recommendation sys-
tems. With this generalization, it is possible for the system to incorporate better product
specifications and user needs. We have also provided guidelines for how to estimate
the necessary probability values. In addition, we have developed a new mechanism
for computing the posterior probabilities for efficient recommendation. Not only does
this behave intuitively, but it is also a promising alternative for recommending environ-
ments.
By way of future work, we are planning to evaluate the model with current problems
with real users in order to determine the quality of the recommendations provided and
to enable a more complex definition of the user profile. This shall also allow us to fine-
tune the system in order to improve system performance. Additionally, we propose to
extend these ideas when recommending in hierarchical domains by incorporating the
decision theory
32

Acknowledgements
This work has been supported by the Spanish Fondo de Investigaci
´
on Sanitaria, under
Project PI021147.
References
1. M. Balabanovic and Y. Shoham. 1997. Fab: Content-based, collaborative recommendation.
Communications of the ACM, 40(3):66–72.
2. J.S. Breese, D. Heckerman, and C. Kadie. 1998. Empirical analysis of predictive algorithms
for collaborative filtering. In Proc. 14th Conf. on Uncertainty in Artificial Intelligence, 43–
52.
3. R. Baeza-Yates and B. Ribeiro-Neto. Modern Information Retrieval. Addison-Wesley, Har-
low, UK, 1999.
4. C.J. Butz. 2002. Exploiting contextual independencies in web search and user profiling. In
Proc. of World Congress on Computational Intelligence, 1051–1056.
5. L.M. de Campos, J.M. Fern
´
andez-Luna, and J.F. Huete. 2003. The BNR model: Foun-
dations and performance of a Bayesian network retrieval model. International Journal of
Approximate Reasoning, 34:265–285.
6. L.M. de Campos, J.M. Fern
´
andez-Luna, and J.F. Huete. 2005. A Decision-Based Approach
for Recommending in Hierarchical Domains. Lecture Notes in Artificial Intelligence (Proc.
ECSQARU 2005), 3571:123-135.
7. L.M. de Campos, J.M. Fern
´
andez-Luna, and J.F. Huete. 2005. e-Bay.Net: Helping Users
to Buy in e-commerce Applications. Soft Computing for information access on the Web:
EUSFLAT05-LFA Conference , To appear.
8. F.V. Jensen. 2001. Bayesian Networks and Decision Graphs. Springer Verlag.
9. S. Kangas. 2002. Collaborative filtering and recommendation systems. VTT Information
Technology, Research report TTE4-2001-35.
10. K. Miyahara and J. Pazzani. 2000. Collaborative filtering with the simple Bayesian classifier.
In Proc. of the Pacific Rim Int. Conf. on Artificial Intelligence, 679–689.
11. P. Nokelainen, H. Tirri, M. Miettinen, and T. Silander. 2002. Optimizing and profiling users
on line with Bayesian probabilistic modelling. In Proc. of the NL Conference.
12. V. Robles, P. Larra
˜
naga, J.M. Pe
˜
na, O. Marb
´
an, J. Crespo, and M.S. P
´
erez. 2003. Collabora-
tive filtering using interval estimation naive Bayes. Lecture Notes in Artificial Intelligence,
2663:46–53.
13. S.N. Schiaffinoand A. Amandi. 2000. User profiling with case-based reasoning and Bayesian
network. Proc. of the Iberoamerican Conf. of Artif. Intelligence, 12–21.
14. S. Wong and C. Butz. 2000. A Bayesian approach to user profiling in information retrieval.
Technology Letters, 4(1):50–56.
33