
CLUSTERING INTERESTINGNESS MEASURES WITH POSITIVE
CORRELATION
Xuan-Hiep Huynh, Fabrice Guillet, Henri Briand
LINA CNRS FRE 2729 - Polytechnic school of Nantes university
La Chantrerie BP 50609 44306 Nantes Cedex 3, France
Keywords:
Interestingness measure, intensity of implication, cluster, objective measure, interestingness property.
Abstract:
Selecting interestingness measures has been an important problem in knowledge discovery in database. A lot
of measures have been proposed to extract the knowledge from large databases and many authors have intro-
duced the interestingness properties for selecting a suitable measure for a given application. Some measures
are adequate for some applications but the others are not, and it is difficult to capture what the best measures
for a given data set are. In this paper, we present a new approach implemented in a tool to select the groups or
clusters of objective interestingness measures that are highly correlated in an application. The final goal relies
on helping the user to select the subset of measures that is the best adapted to discover the best rules according
to his/her preferences.
1 INTRODUCTION
Many interestingness measures have been proposed
in the literature to select the most significant knowl-
edge from a large database in knowledge discovery in
database research such as support, confidence, causal
support, laplace, lift, cosine, gini-index, conviction,
loevinger, yule’s y, intensity of implication entropy’s
version, ... in order to reduce the enormous amount
of rules discovered under the form of association rules
introduced by Agrawal (Agrawal et al., 1993). Each
measure is used with its own characteristics of a given
domain of application so that it is not adequate for a
given domain of application that is strongly different.
There are two types of measures (Freitas, 1999): sub-
jective and objective. Subjective measures (Padman-
abhan and Tuzhilin, 1998) (Liu et al., 1999) depend
on the user who examines the data with his/her ex-
periences while objective measures depend only on
the data structure. The problem of finding interesting
patterns leads to the design of a suitable measure and
the definition of a set of principles or properties (Sil-
berschartz and Tuzhilin, 1996)(Gavrilov et al., 2000)
(Klemettinen et al., 1994) (Brin et al., 1997) (Bayardo
and Agrawal, 1999) (Hilderman and Hamilton, 2001)
(Tan et al., 2004). In our works, we focus on the ob-
jective interestingness measures.
The paper is organized as follows. Section 2
gives the definition and approach with the concepts
of intensity of implication. Section 3 introduces an
overview of interestingness properties proposed in the
literature and determines some mathematical relation
of the measures. Section 4 presents our approach on
cluster analysis. Section 5 gives the first results of our
works in finding the clusters of interestingness mea-
sures. Finally, we conclude and introduce some future
research works.
2 INTENSITY OF IMPLICATION
Gras (Gras, 1996) introduced the theory of statisti-
cal implication, with the concepts of examples and
negative examples (contra-example). We consider the
quality of the implication and determine this quality
with the change of negative examples.
An association rule a ⇒ b is an implication that b
tends to be true once we know a. But it is difficult to
see this case in reality. There is always some nega-
tive examples that b is false when a is true. Intensity
of implication (Gras, 1996) is a measure ϕ(a ⇒ b)
based on the probability model of association rule and
giving the user some thing interesting by considering
the effects of the number of negative examples on the
decision. Intensity of implication is also a robustness
approach for the evaluation of the data set by just tak-
248
Huynh X., Guillet F. and Briand H. (2005).
CLUSTERING INTERESTINGNESS MEASURES WITH POSITIVE CORRELATION.
In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 248-253
DOI: 10.5220/0002508502480253
Copyright
c
SciTePress
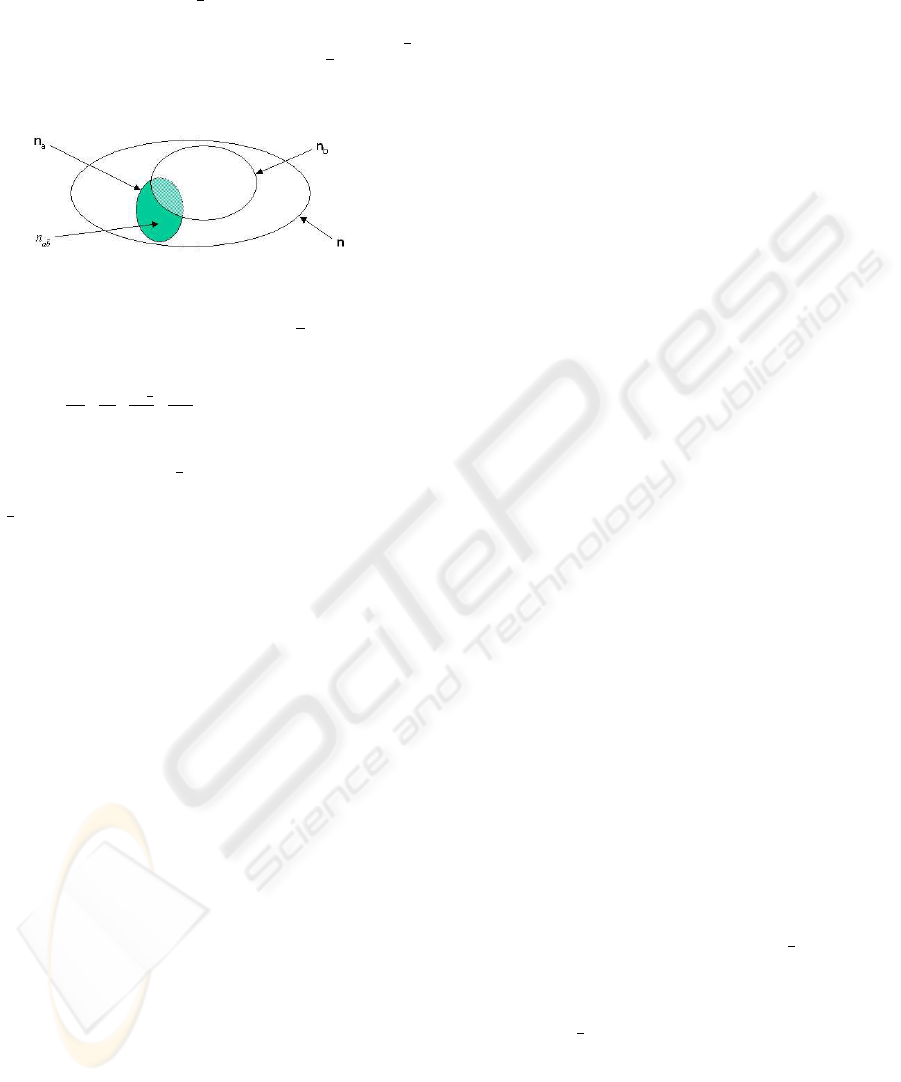
ing in account a small number of negative examples.
Each association rule a ⇒ b must be associated to 4
cardinalities (n, n
a
, n
b
, n
a
b
). More precisely, n is the
number of transactions, n
a
(resp. n
b
) the number of
transactions satisfying the itemset a (resp. b), and n
ab
is the number of transactions satisfying a∧
b (negative
examples).
Figure 1: Cardinalities of a rule a ⇒ b.
With these notions, p(a), p(b), p(a∧b), p(a∧b) are
the probabilities of the premise, conclusion, negative
examples, and examples of the rule respectively com-
puted as:
n
a
n
,
n
b
n
,
n
a
b
n
,
n
ab
n
.
With all the studied interestingness measures, we
are going to calculate as one function f with four
arguments n, n
a
, n
b
, n
a
b
. Then, all the quality mea-
sures will be transformed in terms of n, n
a
, n
b
, and
n
ab
. See Appendix A.
3 INTERESTINGNESS
PROPERTIES
Objective measure is a data-driven, domain-
independent approach to evaluate the quality of
discovered patterns. Piatetsky-Shapiro (Piatetsky-
Shapiro, 1991) proposed three principles for a
suitable rule-interest measure (RI) on a rule a ⇒ b:
(P1) RI = 0 if a and b are statistically independent;
the rule is not interesting, (P2) RI monotonically
increases with p(a ∧ b) when p(a) and p(b) remain
the same, (P3) RI monotonically decreases with p (a)
or p(b) when the rest of the parameters (p(a ∧ b) and
p(b) or p(a)) remain unchanged.
There are many authors who have extended these
principles or proposed new principles:
(Bayardo and Agrawal, 1999) concluded that the
best rules according to any interestingness measures
must reside along a support/confidence border. The
work allows for improved insight into the data and
supports more user-interaction in the optimized rule-
mining process.
(Hilderman and Hamilton, 2001) proposed five
principles for ranking summaries generated from
databases, and performed a comparative analysis of
sixteen diversity measures to determine which ones
satisfy the proposed principles. The objective of this
work is to gain some insight into the behavior that can
be expected from each of the measures in practice.
(Kononenco, 1995) analyses the biases of eleven
measures for estimating the quality of multi-valued
attributes. The values of information gain, j-measure,
gini-index, and relevance tend to linearly increase
with the number of values of an attribute.
(Tan et al., 2004) introduced twenty-one interest-
ingness measures using Pearson’s correlation and has
found two situations in which the measures may be-
come consistent with each other, namely, the support-
based pruning or table standardization are used. In
addition, he also proposed five new interestingness
properties: (1) symmetry under variable permutation,
(2) row/column scaling invariance, (3) anti-symmetry
under row/column permutation, (4) inversion invari-
ance, and (5) null invariance, to capture the utility
of an objective measure in terms of analyzing k-way
contingency tables.
Our approach is different because we consider the
data set values with the intensity of implication mea-
sure, taking into account the number of negative ex-
amples in the data sets, while the other authors have
investigated the properties of interestingness on the
basis of their own approaches, not on the data set.
Furthermore, we have found some relations in
mathematical formulae of the quality measures. This
work is useful and interesting for reducing the quan-
tity of measures. If one measure strongly depends on
the other measures, we will not consider it any more.
For example: T auxDeLiaison = Lift − 1, we will
only select Lift for both of them. See Appendix B.
4 CLUSTER ANALYSIS
4.1 Correlation
We extended the definition of similarity between two
associations patterns introduced by Tan (Tan et al.,
2004):
Let R(D) = {r
1
, r
2
, ..., r
p
} denote input data as
a set of p association rules derived from a data set
D. Each rule a ⇒ b is described by its itemsets
(a, b) and its cardinalities (n, n
a
, n
b
, n
a
b
). Let M
be the set of q available measures for our analysis
M = {m
1
, m
2
, ..., m
q
}. Each measure is a numer-
ical function on rule cardinalities: m(a ⇒ b) =
f(n, n
a
, n
b
, n
a
b
).
For each measure m
i
∈ M , we can construct a vec-
tor m
i
(R) = {m
i1
, m
i2
, ..., m
ip
}, i = 1..q, where
m
ij
corresponds to the calculated value of the mea-
sure m
i
for a given rule r
j
.
The correlation value between any two measures
m
i
, m
j
{i, j = 1..q} on the set of rules R will be cal-
culated by using a Pearson’s correlation coefficient
CLUSTERING INTERESTINGNESS MEASURES WITH POSITIVE CORREALTION
249

CC (Saporta, 1990), where m
i
, m
j
are the average
calculated values of vector m
i
(R) and m
j
(R) respec-
tively.
CC(m
i
, m
j
) =
P
p
k=1
[(m
ik
−
m
i
)(m
jk
− m
j
)]
p
[
P
p
k=1
(m
ik
−
m
i
)
2
][
P
p
k=1
(m
jk
− m
j
)
2
]
Definition 1. Strongly positive/negative correlated
measures. Two measures m
i
and m
j
are strongly pos-
itive (resp. negative) correlated to each other with re-
spect to the data set D if the correlation value between
m
i
and m
j
is greater (resp. lower) than or equal to a
threshold t
g
(resp. t
l
).
Definition 2. Uncorrelated measures. Two mea-
sures m
i
and m
j
are uncorrelated to each other with
respect to the data set D if the absolute value of the
correlation between them is lower than or equal to a
critical value t
u
.
In our experiment, we use t
g
= 0.85, t
l
= −0.85,
and t
u
= 1.960 ×
1
√
p
(a level of significance of the
test α = 0.05 for hypothesis testing) in a population
p because of their wide acceptation in the literature.
Definition 3. Positively correlated cluster. A con-
nected component of the graph that is based on the
similarity matrix in which each strongly positive cor-
relation between two measures represents an edge, it
is a positively correlated cluster.
4.2 A quick description of data and
measures used
We have applied our experiments on the rule set of
120000 association rules. The rules have been ex-
tracted from the ”Mushroom” data set by using the
Apriori algorithm (Agrawal and Srikant, 1994). The
Mushroom data set is issued from one of the categor-
ical data set from Irvine machine-learning database
repository (Blake and Merz, 1998).
In our experiment, we compared and analyzed 34
interestingness measures (see Appendix A for com-
plete definitions).
As announced, we will present some interesting re-
sults of the Mushroom data set, focusing on cluster
results.
5 FIRST RESULTS ON CLUSTER
ANALYSIS
5.1 Distributions
Frequent and inverse-cumulative histograms are in-
troduced to present the frequency of values calcu-
lated from the measures in one cluster. The minimum,
maximum, average, skewness and kurtosis values are
computed in order to allow the user to have a first view
of all the measures in the cluster (Fig. 2).
Figure 2: Distribution of one cluster from Mushroom data
set.
We have determined all the scatter plots that can be
generated from every pair of measures, and it takes
a lot of time to draw the images. Some scatter plots
(Fig. 3) are illustrated from the Mushroom data set.
Figure 3: The strongly positive correlation of one cluster
from Mushroom data set (extract).
5.2 Strongly positive correlation
The strongly positive correlations in each cluster of
the data set are introduced in order to find the most
interesting patterns according to the reason why the
measure is proposed. For example, the correlation
value between Cosine and Jaccard is 0.9673, so we
can see the correlation image is close to linear correla-
tion. But in reality, it is not true that a high correlation
value always has a linear correlation, the conclusion
also depends on the form of the image obtained (Fig.
3).
5.3 Weighted graph representation
To have an intuitive view of a cluster, a weighted
graph is introduced. A vertex is based on the mea-
sure name and an edge is the correlation value be-
tween the two measures. The value assigned for the
ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
250
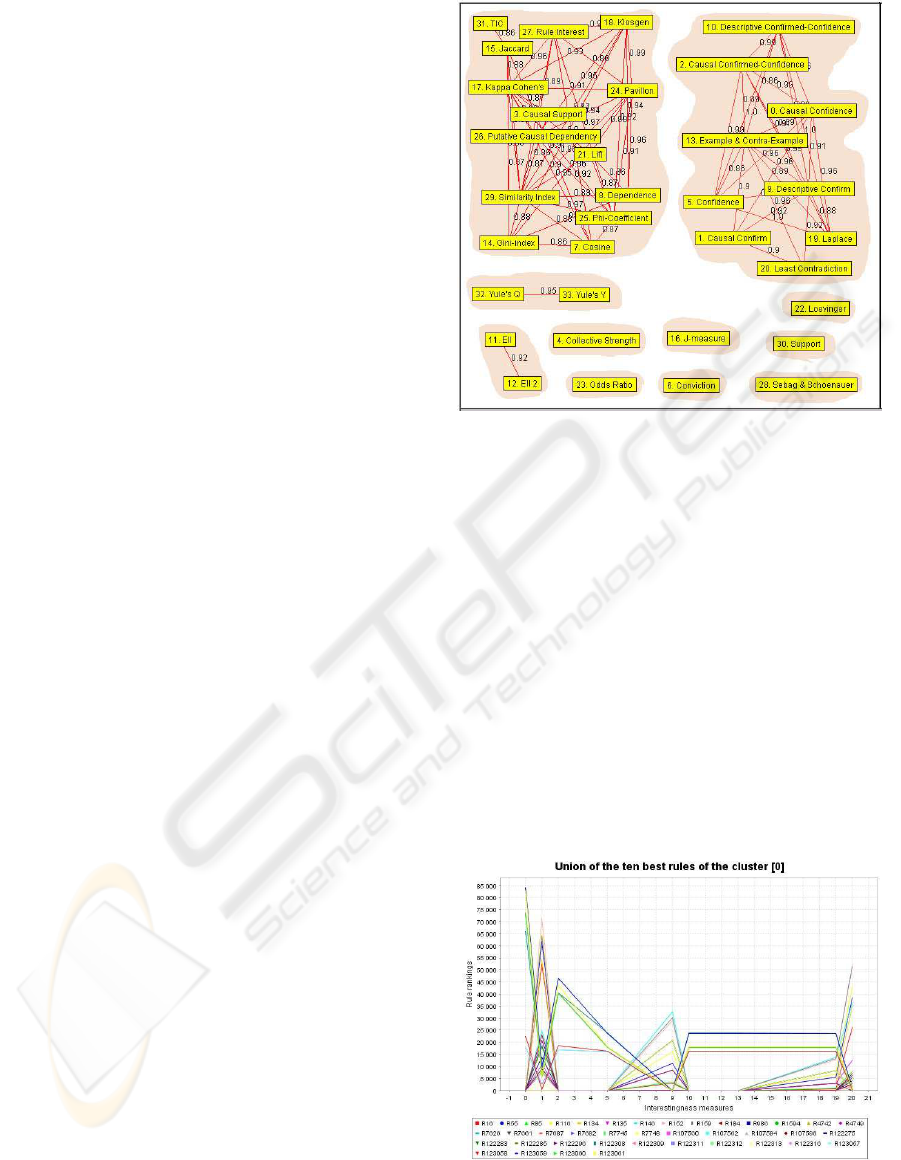
edge is given from the strongly positive correlation
value (see Fig. 4).
Based on the strongly positive correlation and con-
structed with the weighted graph, we have found
eleven positively correlated clusters (Fig. 4):
- (C0) Least Contradiction, Causal Confirm,
Laplace, Confidence, Descriptive Confirm, Exam-
ple & Contra-Example, Causal Confidence, Causal
Confirmed-Confidence, Descriptive Confirmed-
Confidence. These measures have formed the
cluster because most of these measures are issued
from confidence measure.
- (C1) Cosine, Gini-index, Phi-Coefficient, Similar-
ity Index, Dependence, Lift, Putative Causal De-
pendency, Causal Support, Kappa Cohen’s, Pavil-
lon, Jaccard, Rule Interest, TIC, Klosgen.
- (C2) Yule’s Q and Yule’s Y are the measures
that form a cluster, the same result as Tan (Tan
et al., 2004) with the effect of the second property,
row/column scaling invariance. This conclusion is
not very surprising because of our demonstration
in Section 3 these measures are functionally depen-
dent (See Appendix B for more details).
- (C3) EII and EII 2, the two entropic versions of the
measure Intensity of Implication. These two mea-
sures are issued from the change of one parame-
ter in their formula (α = 1 or α = 2) (Blanchard
et al., 2003), so this cluster is naturally and strongly
within-related.
- (C4..C10) Seven clusters with a single measure:
Collective Strength, Odds Ratio, J-measure, Con-
viction, Loevinger, Support, and Sebag & Schoe-
nauer, which are not strongly correlated to other
ones.
5.4 Best rules
5.4.1 Intersection of the ten best rules
We choose the ten best rules of each positive cluster
and give the user an overview of their intersection.
The rank of each rule is used to validate the result.
The Y-axis holds the rank of the rule for the corre-
sponding measure. Each rule is represented with par-
allel coordinates among interestingness measure val-
ues (see Fig. 5). We can see the intersection in a
horizontal line and if we obtain many rules having the
same rank value so we will print these rules with only
one line. If the user want to capture a small group
of the best rules for making their decision, he/she can
use these rules for their first choice.
Figure 4: Weighted graph from Mushroom data set.
5.4.2 Union of the ten best rules
With the same technique as above, we introduce the
union of the ten best rules in each cluster, in order to
give the user a more specific view in the cluster . The
measures have the set of highest ranks (more interest-
ing) rely on the low value of the Y-axis. With the con-
centration lines on low rank values, we can capture
3 measures: Confidence(5), Descriptive Confirmed-
Confidence (10), and Example Contra-Example (13)
that are suitable for all of the best rules in this cluster
(see Fig. 5).
Figure 5: Within-cluster union of one positive cluster from
Mushroom data set.
CLUSTERING INTERESTINGNESS MEASURES WITH POSITIVE CORREALTION
251

5.5 Clusters in relation to a selected
cluster
With the same technique used in the Section 5.4, we
introduce the two following views :
5.5.1 Union of all the clusters in relation to the
current cluster
Based on the ten best rules in the current cluster, we
draw the parallel coordinates of each rule on other
clusters. The user can see the zone that is the most
interesting with the highest value. The effect of the
ten best rules on the other clusters gives the user a
general sampling of the entire cluster. With the union
approach, many best rules may be presented and com-
pared.
5.5.2 Intersection of all the clusters in relation to
the current cluster
By decreasing the quantity of best rules in one clus-
ter, we will observe the rank distribution. The inter-
section is less interesting than the union because we
generally do not have any interesting zone. Using the
intersection in relation to the current cluster is impor-
tant when the user just finds a small set of interesting
and close rules.
6 CONCLUSION
This work has led to the implementation of a tool em-
bedding more than 8000 lines of Java codes for the
analysis of data set characteristics, quality measure
sensitivity, correlations, clustering and ranking.
We have found and identified eleven clusters from
all the quality measures studied on the Mushroom
data set. We have also proposed a way to study the
ten best rules of each cluster, the union and intersec-
tion of the ten best rules of all the cluster in relation to
the current cluster. The union of the ten best rules for
all the clusters is also presented for the user’s choice.
For the first presentation of our results, we just use
thirty four measures for implementation.
Our future research will focus on improving the
clustering of measures: (1) in designing a better sim-
ilarity measure than the linear correlation, (2) in se-
lecting the best representative measure in a cluster.
REFERENCES
Agrawal, R., Imielinski, T., and Swami, A. (1993). Mining
association rules between sets of items in large data-
bases. In Proceedings of 1993 ACM-SIGMOD Inter-
national Conference on Management of Data.
Agrawal, R. and Srikant, R. (1994). Fast algorithms for
mining association rules. In Proceedings of the 20th
VLDB Conference.
Bayardo, J. and Agrawal, R. (1999). Mining the most in-
terestingness rules. In Proceedings of the Fifth ACM
SIGKDD International Confeference On Knowledge
Discovery and Data Mining.
Blake, C. and Merz, C. (1998). UCI Repos-
itory of machine learning databases,
http://www.ics.uci.edu/∼mlearn/MLRepository.html.
University of California, Irvine, Dept. of Information
and Computer Sciences.
Blanchard, J., Kuntz, P., Guillet, F., and Gras, R. (2003).
Implication intensity: from the basic statistical defin-
ition to the entropic version. In Statistical Data Min-
ing and Knowledge Discovery. Chapman & Hall, CRC
Press.
Brin, S., Motwani, R., and Silverstein, C. (1997). Beyond
market baskets: Generalizing association rules to cor-
relation. In Proceedings of ACM SIGMOD Confer-
ence.
Freitas, A. (1999). On rule interestingness measures. In
Knowledge-Based Systems, 12(5-6).
Gavrilov, M., Anguelov, D., Indyk, P., and Motwani, R.
(2000). Mining the stock market: which measure is
best? In Proceedings of the Sixth International Con-
ference on Knowledge Discovery and Data Mining.
Gras, R. (1996). L’implication statistique - Nouvelle
m
´
ethode exploratoire de donn
´
ees. La pens
´
ee sauvage
´
edition.
Hilderman, R. and Hamilton, H. (2001). Knowledge Dis-
covery and Measures of Interestingness. Kluwer Aca-
demic Publishers.
Klemettinen, M., Mannila, H., Ronkainen, P., Toivonen, H.,
and Verkano, A. I. (1994). Finding interesting rules
from larges sets of discovered association rules. In the
Third International Conference on Information and
Knowledge Management. ACM Press.
Kononenco, I. (1995). On biases in estimating multi-valued
attributes. In Proceedings of the Fourteenth Interna-
tional Joint Conference on Artificial Intelligence (IJ-
CAI’95).
Liu, B., Hsu, W., Mun, L., and Lee, H. (1999). Finding
interestingness patterns using user expectations. In
IEEE Transactions on Knowledge and Data Mining
11(1999).
Padmanabhan, B. and Tuzhilin, A. (1998). A belief-
driven method for discovering unexpected patterns.
In Proceedings of the 4th international conference on
Knowledge Discovery and Data Mining.
Piatetsky-Shapiro, G. (1991). Discovery, analysis and pre-
sentation of strong rules. In Knowledge Discovery in
Databases. MIT Press.
Saporta, G. (1990). Probabilit
´
es, Analyse des Donn
´
ees et
Statistique. Editions Technip, Paris.
ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
252

Silberschartz, A. and Tuzhilin, A. (1996). What makes pat-
terns interesting in knowledge discovery systems. In
IEEE Transaction on Knowledge and Data Engineer-
ing (Vol. 8, No. 9).
Tan, P., Kumar, V., and Srivastava, J. (2004). Selecting the
right objective measure for association analysis. In
Information Systems 29(4).
Appendix B. Relation between measures
N
◦
Formulae
0 Laplace =
Conf idence×(n×Support+1)
n×Support+2×Con f idence
1 RuleInterest =
S upport
Conf idence
× P avillon
2 Lift =
Conf idence
Conf idence−P avillon
3 W ang =
S upport
Conf idence
× (Confidence − α)
4 Gray&Orlowska =
(Lift
k
− 1) × (Support − RuleInterest)
m
5 J − measure = Support × log
2
(Lift) + (Support
−DescriptiveConf irm) × log 2(
1
Conviction
)
6 J − measurevariant = Support × log
2
(Lift)
7 Jaccard =
S upport
S upport
Conf idence
+Conf idence−P avillon−Support
8 Loevinger = 1 −
1
Conviction
9 Consine =
S upport
√
S upport−RuleInterest
10 CausalConf irm = CausalSupport − 2 × Support+
2 × Descriptiv eConf irm
11 CausalConf irmed − Conf idence =
DescriptiveConf irmedConf idence − Conf idence+
CausalConf idence
2
12 Consine
2
= Lif t × Support
13 RuleInterestvariant = |RuleInterest|
14 T auxDeLiaison = Lift − 1
15 Y ule
′
sQ =
OddsRatio−1
OddsRatio+1
16 Y ule
′
sY =
√
OddsRatio−1
√
OddsRatio+1
17 Example&Contra − Example =
DescriptiveConf irm
Conf idence−P avillon
18 LeastContradiction =
DescriptiveConf irm
19 Klosgen =
√
Support × P avillon
20 Sebag&Schoenauer =
S upport
S upport−DescriptiveConf irm
Appendix A. Quality measures
N
◦
Interestingness Measure f(n, n
a
, n
b
, n
a
b
)
0 Causal Confidence 1 −
1
2
(
1
n
a
+
1
n
b
)n
a
b
1 Causal Confirm
n
a
+n
b
−4n
ab
n
2 Causal Confirmed-Confidence 1 −
1
2
(
3
n
a
+
1
n
b
)n
a
b
3 Causal Support
n
a
+n
b
−2n
ab
n
4 Collective Strength
(n
a
−n
a
b
)(n
b
−n
a
b
)(n
a
n
b
+n
b
n
a
)
(n
a
n
b
+n
a
n
b
)(n
b
−n
a
+2n
a
b
)
5 Confidence 1 −
n
a
b
n
a
6 Conviction
n
a
n
b
nn
a
b
7 Cosine
n
a
−n
a
b
√
n
a
n
b
8 Dependence |
n
b
n
−
n
a
b
n
a
|
9 Descriptive Confirm
n
a
−2n
a
b
n
10 Descriptive Confirmed-Confidence 1 − 2
n
a
b
n
a
11 EII (α = 1) ϕ × I
1
2α
12 EII (α = 2) ϕ × I
1
2α
13 Example & Contra-Example 1 −
n
a
b
n
a
−n
a
b
14 Gini-index
(n
a
−n
a
b
)
2
+n
2
a
b
nn
a
+
(n
b
−n
a
+n
a
b
)
2
+(n
b
−n
ab
)
2
nn
a
−
n
2
b
n
2
−
n
2
b
n
2
15 Jaccard
n
a
−n
a
b
n
b
+n
a
b
16 J-measure
n
a
−n
a
b
n
log
2
n(n
a
−n
a
b
)
n
a
n
b
+
n
a
b
n
log
2
nn
a
b
n
a
n
b
17 Kappa Cohen’s
2(n
a
n
b
−nn
ab
)
n
a
n
b
+n
a
n
b
18 Klosgen
n
a
−n
a
b
n
(
n
b
n
−
n
a
b
n
a
)
19 Laplace
n
a
+1−n
a
b
n
a
+2
20 Least Contradiction
n
a
−2n
a
b
n
b
21 Lift
n(n
a
−n
a
b
)
n
a
n
b
22 Loevinger 1 −
nn
a
b
n
a
n
b
23 Odds Ratio
(n
a
−n
a
b
)(n
b
−n
a
b
)
n
a
b
(n
b
−n
a
+n
ab
)
24 Pavillon
n
b
n
−
n
a
b
n
a
25 Phi-Coefficient
n
a
n
b
−nn
a
b
√
n
a
n
b
n
a
n
b
26 Putative Causal Dependency
3
2
+
4n
a
−3n
b
2n
− (
3
2n
a
+
2
n
b
)n
a
b
27 Rule Interest
1
n
(
n
a
n
b
n
− n
a
b
)
28 Sebag & Schoenauer 1 −
n
a
b
n
a
−n
a
b
29 Similarity Index
n
a
−n
a
b
−
n
a
n
b
n
n
a
n
b
n
30 Support
n
a
−n
a
b
n
31 TIC T I(a → b) × T I(b → a)
32 Yule’s Q
n
a
n
b
−nn
ab
n
a
n
b
+(n
b
−n
b
−2n
a
)n
a
b
+2n
2
a
b
33 Yule’s Y
(n
a
−n
a
b
)(n
b
−n
ab
)−
n
a
b
(n
b
−n
a
+n
ab
)
(n
a
−n
a
b
)(n
b
−n
ab
)+
n
a
b
(n
b
−n
a
+n
ab
)
CLUSTERING INTERESTINGNESS MEASURES WITH POSITIVE CORREALTION
253
