
SYNTHESISE WEB QUERIES
Search the Web by Examples
Vishv Malhotra, Sunanda Patro, David Johnson
School of Computing, Private Box 100, University of Tasmania, Hobart 7001 Australia
Keywords: Boolean expression, web search query, web search engine, World Wide Web, Recall and precision of query
Abstract: An algorithm to synthesise a web search query from example documents is described. A user searching for
information on the Web can use a rudimentar
y query to locate a set of potentially relevant documents. The
user classifies the retrieved documents as being relevant or irrelevant to his or her needs. A query can be
synthesised from these categorised documents to perform a definitive search with good recall and precision
characteristics.
1 INTRODUCTION
The primary contribution of the paper is an
algorithm that synthesises web search queries from
examples of text documents categorised as relevant
and irrelevant to the needs of a web searcher. The
synthesised query would locate web links to
resources relevant to the searcher as inferred from
the examples. The three primary objectives for the
algorithm are to ensure that the synthesised query
has good recall; good precision; and not the least, is
of a form and size acceptable to the intended search
engine (Sebastiani 2002, Brin and Page 1998).
The rest of this paper is organised as follows.
Sect
ion 2 gives an overview of the algorithm and
uses examples to explain and provide a context for
later sections. Sections 3, 4 and 5 describe the three
main building block of the query synthesiser. Some
of the issues arising from the algorithm and its
current implementation are discussed in the final
section.
2 PRELIMINARIES
A literal is an expression that is either a single term
or its negation. In this paper, Boolean operator NOT
(!) takes precedence over other Boolean operators.
A minterm is a sequence of literals combined by
Boolean operator AND (&). We would use Google
convention to use AND (&) as lowest precedence
and implied (not explicitly written) operator. A
sequence of minterms combined by Boolean OR (|)
operation is disjunctive normal form (DNF) of the
Boolean expression. A maxterm is a sequence of
literals combined by Boolean OR operations. A
Boolean expression is in conjunctive normal form
(CNF) if it is made of maxterms combined by
operator AND. For further information about the
Boolean expressions the reader may wish to see
(Aho and Ullman, 1992) as an excellent reference.
A se
arch query is suitably compacted
representation of a DNF Boolean expression with at
least one positive literal in each minterm. To help
presentation of the algorithms in the later sections,
we define a selection operation σ: For a set of
textual documents, D, and a search query, Q,
expression D σ Q will be used to denote a search
by query Q over set D. An operational interpretation
of expression D σ Q is as follows:
Case: Q is ter
m {doc | doc ∈ D and
term occurs in document
doc}
Case: Q is !te
rm {doc | doc ∈ D &
term does not occur in
document doc}
Case: Q is (R &
S) (D σ R)
σ S
Case: Q is (R |
S) (D σ R) ∪ (D σ S)
The current implementation of the query
syn
thesis algorithm requires the initial search query
for retrieving example relevant and irrelevant
documents to be a minterm comprising of positive
literals. In this paper, the terms in the initial query
minterm are deemed to occur in each document. A
real document may not have query terms because
search engines use, in addition to the text in the
291
Malhotra V., Patro S. and Johnson D. (2005).
SYNTHESISE WEB QUERIES - Search the Web by Examples.
In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 291-296
DOI: 10.5220/0002510202910296
Copyright
c
SciTePress
document, text near the links to the document in the
other documents to index the linked document.
For a set, S, |S| denotes its cardinality – the
number of elements in the set. For example, for a
Boolean expression BE and sets Relevant and
Irrelevant we define its precision as: precision(BE)
= |Relevant σ BE|/|Irrelevant σ BE|. The case where
denominator is 0 is handled by assigning a suitable
large value as precision.
The five main steps in the query synthesis
algorithm are:
i. Construct CNF (conjunctive normal form)
Boolean expression that selects every document
in set Relevant and rejects documents in set
Irrelevant. This expression is typically long
with many terms and Boolean operators to be
efficient and effective search queries. See
Section 3 for more details.
ii. Convert CNF Boolean expression into an
equivalent DNF Boolean expression. Remove
redundant minterms from the DNF expression.
These minterms will be called p-minterms. Step
5 would modify the p-minterms to aid
construction of an acceptable size search query.
This will be discussed further in Section 3.1.
iii. Synthesise a Boolean expression Query by
assembling a subset of minterms such that
Query selects every document in set Relevant.
Rewrite Query in a form suitable to the chosen
web search engine. Details are in Section 4.
iv. If Query is acceptable to the search engine, stop.
Boolean expression Query is the required search
query. Otherwise,
v. Derive a set of minterms from p-minterms that
supports synthesis of a better balanced search
query. Go back to step 3 to synthesise a new
candidate query. Section 5 deals with this issue.
2.1 Examples
To set a context and explain the steps in the
algorithms, some example queries are given in Table
1. These queries were run over Google search engine
to locate links to resources. A query with a single
term (naïve query) was initially generated to retrieve
documents for defining sets Relevant and Irrelevant.
Only text documents are included in these sets.
These sets are then used to synthesise a new query.
The case of query regarding rainbow needs some
further comments. In this case, the initial set
Relevant had very few (three) documents for an
effective synthesis of a query. The synthesised
query (rainbow sky) did not perform well.
However, the query synthesised from the documents
retrieved by this query proved to be a good search
query.
3 CONSTRUCT CNF BOOLEAN
EXPRESSION
The search query synthesis begins with construction
of a CNF Boolean expression that selects all relevant
documents and rejects irrelevant documents. The
Boolean expression can be constructed by repeatedly
constructing maxterms to cover all relevant
documents and reject many irrelevant documents.
Sanchez, Triantaphyllou, Chen and Liao (2002) have
reported an algorithm for maxterm construction by
endeavouring to reject the irrelevant documents that
have not been rejected by the previously constructed
maxterms. Thus, after each successive stage, the
conjunction of maxterms rejects more irrelevant
documents.
We make two important changes to the reported
algorithm to make it suitable for synthesising search
queries.
i. We construct maxterms containing only positive
literals. This conservative arrangement is
appropriate because sets Relevant and Irrelevant
do not characterise a closed world of
documents.
Table 1: Examples of queries accessed using Google search engine. Type indicates the source of the query: naïve
synthesised using the algorithm described in this paper, or a first attempt by a human.
Purpose
& Type
Search query Query
size
Relevant
accessed
Irrelevant
accessed
Information about radioactive element Radium.
Naive radium 1 19 41
Synthetic radium (((element | period) number) | ((element | metal) uranium)) 7 62 8
Human radium element radioactive 3 50 20
Information regarding rainbow that appear in sky after a rain.
Naive rainbow 1 3 52
Synthetic (rainbow sky) 2 16 48
Synthetic rainbow light (raindrop | higher | copyright | solar | (hand index dark)) 9 43 27
Human (rainbow rain color) 3 37 33
ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
292

ii. Each term (word in the example documents) is
prioritised to reflect its potential as the next
candidate term in the maxterm under
construction.
Definition
The potential of a candidate term is defined by the
number of new relevant and irrelevant documents it
selects. The potential for term t during construction
of (i+1)
st
maxterm is computed as follows
(maxterm
p
is the partially constructed (i+1)
st
maxterm):
TR = Relevant – (Relevant σ maxterm
p
);
TR
t
= TR σ t;
TIR = Irrelevant σ (maxterm
1
& …& maxterm
i
));
TIR
t
= TIR σ t;
Potential(t) =
((|TR
t
|)(|TIR|–|TIR
t
|))/((|TR|–|TR
t
|+1)(|TIR
t
|+1)).
□
An algorithm for constructing CNF Boolean
expression is shown in Figure 1. The algorithm
terminates successfully when a conjunction of
maxterms rejects every irrelevant document. The
changes made to the algorithm could, in some rare
cases, lead to a failed run of function
Build_Maxterm. If all terms in a relevant document
are also in an irrelevant document then it is not
possible to find a term for a maxterm that would
select the relevant document but would reject the
irrelevant document. It is practical to remove these
irrelevant documents from set Irrelevant. The price
for this action is a small reduction in the precision of
the synthesised query.
3.1 Eliminate Boolean Expression
Redundancies
The Boolean expressions constructed by algorithm
Build_CNF_BE frequently has too many terms for
an effective and efficient processing by the web
search engines. As an example of a constructed
Boolean query consider the case of search for
information about rainbow shown in Table 1.
Starting with query (rainbow sky) a set of 16
relevant and 48 irrelevant documents were
identified. The Boolean expression for this example
is: rainbow (raindrop | arc | prism | solar | term |
bow | hand) (air | higher | band | design | contact |
sunlight | american) (red | copyright | download |
index) (light) (water | green | board | dark).
Clearly, the query is not suitable for a Google
search.
To eliminate some redundancy the synthesised
CNF Boolean expression can be transformed into an
equivalent DNF expression using the distribution
property: A (B | C) ≡ (A B) | (A C). The application
Build_CNF_BE
Input: Relevant, Irrelevant, Original Query.
Output: BoolExp
Description: BoolExp selects all documents in set Relevant and rejects virtually all documents in set Irrelevant.
TIR := Irrelevant;
for (i := 1; TIR != {}; i++) {
Maxterm
:= Build_Maxterm(Relevant, TIR);
i
If (no Maxterm
i
possible) break;
TIR := Temp σ Maxterm
i
;
}
BoolExp := (Initial Query) & Maxterm
1
& Maxterm
2
& …;
Build_Maxterm
Input: Relevant, TIR
Output: maxterm
Description: maxterm selects every document in set Relevant and rejects some document in set TIR
TR := Relevant;
for (j := 1; TR != {}; j++) {
Candididate_terms_sorted := sort_candidates(set_of_terms_in(TR));
Term
j
:= Randomly_select_one_from_top_n(Candidate_terms_sorted);
TR := TR – (TR σ Term
j
);
}
maxterm := (Term
1
| Term
2
| …| Term
j
);
Figure 1: Algorithm to construct a Boolean expression that selects all relevant documents and reject irrelevant
documents.
SYNTHESISE WEB QUERIES: Search the Web by Examples
293

of this rule would generate 7x7x4x4=784 minterms,
each with 6 (or fewer) terms for the above example.
Equivalence of two forms of the Boolean expression
– the original CNF and the transformed DNF –
implies that each minterm would reject each
document in set Irrelevant. The set of minterms in
the DNF Boolean expression collectively select
every document in set Relevant. However, an
individual minterm may or may not select any
document in set Relevant. Minterms that do not
select any document in set Relevant are redundant
and can be removed. All but 241 minterms of the
original 748 minterms in DNF Boolean expression
for the rainbow query were removed through an
application of this rule.
We also remove those minterms from this set
that select a proper subset of relevant documents
selected by another minterm in the set. As a further
step in redundancy reduction, terms are removed
from minterms if their removal does not lead to
selection of an irrelevant document. The minterms
surviving these purges constitutes p-minterms (p
signifies precise, perfect or preferred).
4 SEARCH QUERY: MINIMUM
MINTERM COVER FOR SET
RELEVANT
A minimal set of minterms that selects each
document in set Relevant constitutes a search query.
The set of p-minterms collectively selects all
documents in set Relevant. At the same time, a
document may be selected by several minterms. For
example, the query concerning rainbow has 16
relevant documents, but has 241 p-minterms. No
more than 16 minterms are needed to select 16
documents. As the minimisation problem is in NP-
Complete, we use a heuristic to construct a minterm
cover for set Relevant.
A number of heuristics are possible to meet the
goal of keeping the size of the query small while
covering every document in set Relevant. The
Search query synthesis heuristic we use, builds
covering minterm set by selecting a minterm at a
time from the set of available minterms. A greedy
choice is made to select the minterm based on the
number of new relevant documents selected by the
minterm divided by the increase in the query size.
Apte, Damerau and Weiss (1994) have reported
a more sophisticated heuristic for a similar problem.
In their approach, an augmentation is either an
addition of a new minterm to the query or is a
substitution of a minterm in the query with another
minterm. In our heuristic, we derive similar benefits
by using a genetic algorithm approach. We construct
the query several times by starting with a randomly
selected first minterm. The query with the smallest
number of terms is affirmed as the search query.
Given a set of minterms comprising a query it is
useful to define function minimise to transform the
set into a query acceptable to Google (or some other)
search engine. We use the number of terms in this
minimised query as its size. An exact syntax of an
acceptable query for Google is not well defined.
Thus, we use a simplistic algorithm to minimise the
query representation. To construct a minimal query
from a given set of minterms the function identifies
a term that occurs most frequently in the query
minterms. The set of minterms can be partitioned
into two sets.
i. A set of minterms that do not contain the
identified term.
ii. The set of minterms that contains the term. The
term is factored out of these minterms by using
equivalence: (A B)|(A C) ≡ A (B | C).
The minimisation function is then applied
recursively to two sets to take advantage of other
terms that can be used to reduce the query size. As
an example consider the DNF expression: (radium
element number) | (radium period number) | (radium
element uranium) | (radium metal uranium). The
expression has 12 terms. The number of terms can
be reduced to 7 by the minimisation algorithm
leading the following query: radium (((element |
period) number) | ((element | metal) uranium)).
Deeply nested expressions may not be accepted by
some search engines. Consequently we would avoid
synthesising such queries.
In our experiments we noticed only a few cases
of queries with more than 10 terms when
synthesised from p-minterms. Typical query is well-
sized for the search engines. An oversize query for
the rainbow example is: rainbow ((raindrop light) |
(((higher red) | solar) water) | (bow copyright) |
(term red) | (hand index dark)).
5 FITTING QUERY TO SEARCH
ENGINE
If a synthesised query has too many terms it needs
modifications to help synthesise acceptable queries.
This issue will be discussed in this section.
Size of a query can be reduced to fit it to the
constraints of a search engine. However, it would
attract cost in terms of loss in its ability to select all
relevant documents or not being able to avoid all
irrelevant documents. If query size is reduced by
reducing its ability to select all relevant documents,
we need to perform supplementary searches to
ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
294
r
ainbow
t
erm
r
ed
rainbow solar water
rainbow higher red water
account for the documents that we might miss.
Human users tend to use this mode of search. If a
query fails to return a satisfying collection of
relevant links, the query is modified to seek other
links of interest. In contrast to human-controlled
interactive web session, the aim of a synthesised
query is to make each search comprehensive by
keeping the recall at its highest level and seek to
reduce query size by sacrificing precision. Thus, we
seek a query that meets the constraints of the search
engine and selects every document in set Relevant.
However, in addition it may select documents in set
Irrelevant. The goal is to minimise the number of
selected documents from the latter set.
For the oversized query for rainbow, the query
can be made smaller in size by removing terms (for
example) water, solar, higher or red. A term is
removed by replacing it by Boolean constant true.
The terms in the initial query are not available for
removal as such a change may alter the membership
of sets Relevant and Irrelevant. Each removal of
term from a query affects its size differently. For
example, the rainbow query will be one term smaller
if one of the terms, water, higher or red is removed
from it. It will be smaller by three terms if term
solar is removed.
A removal of a term from a minterm may cause
it to select a few irrelevant documents. Thus, there is
a lowering in minterm’s ability to reject irrelevant
documents. As an approximation, we measure the
precision of a query by the minimum precision of its
composing minterms. Consequently, query obtained
by removing term water has precision minimum
{precision(rainbow solar), precision(rainbow higher
red)}. On the other hand, if term solar is removed, it
will be precision(rainbow water). The irrelevant
documents are likely to have lower correlation
among distributions of query terms. These
observations lead us to a simple and effective
method for reducing the query size by lowering their
precision in a controlled way.
The method involves replacing two or more p-
minterms by a single minterm implied by each of the
p-minterms. The replacing minterm selects all
relevant documents selected by the replaced p-
minterms. It has fewer terms thus helping the
synthesised query to be smaller in size. However,
the query would have some lowering of its ability to
reject all irrelevant documents.
Alternately, one could attempt to create smaller
queries by defining minterms at lower precision
values by removing one or more terms from p-
minterms. However, such an approach may generate
a lot of minterms with only marginal advantage in
reducing the query size. The method suggested in
the previous paragraph is able to generate a well
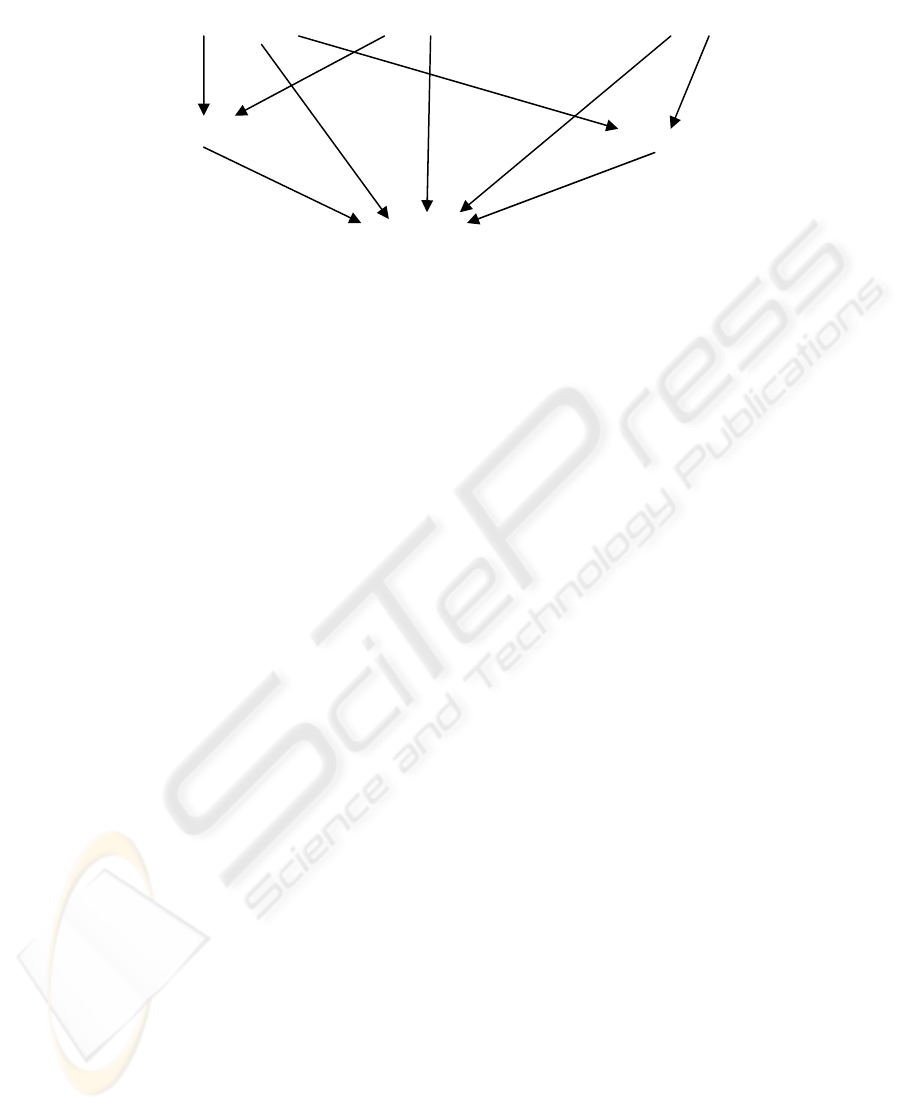
spread lattice of minterms (see Figure 2) to
synthesise query near any required precision value.
A reduction in size of a synthesised but oversize
query by removal of some terms from its minterms
must compete against other queries that may be
synthesised through similar concessions. Thus, the
query synthesis is repeated whenever minterms have
been affected by a transformation that alters their
precisions.
The rest of this section contains a series of
definitions that provide an outline of a method for
constructing sets of minterms from p-minterms. The
basic idea will be to give a method for deriving
implied minterms from the given set of p-minterms.
Next we will define a set by selecting minterms
meeting a stipulated precision property. The set will
be called a set of good minterms. An important
property of p-minterms that the set preserves is the
ability to cover all relevant documents. Thus, using
minterms in the set, one can synthesise a query at a
precision value matching the precision of the
minterms in the set. If the query turns out to be too
r
ainbow
r
ed
rainbow water
…
rainbow (Initial query)
Figure 2: A part of lattice spawned by p-minterms for rainbow query.
SYNTHESISE WEB QUERIES: Search the Web by Examples
295

large, the synthesis is repeated by constructing a new
set of good minterms at the next lower precision
level for which minterms can be found. The initial
query guarantees that the repetitions will eventually
terminate successfully; in the worst case we may
have the initial query as the best query for the
search.
Definition
Let R and S be two sets of minterms, coalesce(R, S)
is a set of minterms defined as follows:
coalesce(R,S) = {π(r,s) | r ∈R and s ∈S },
where π is defined as follows:
π(m
1
,m
2
) = m, where m is a minterm such that
m
1
⇒ m, m
2
⇒ m, and for every minterm m’
(m
1
⇒m’⇒m; m
2
⇒m’⇒m) ⇒ (m’≡m). □
Definition
Let M be a set of p-minterms. We derive set of all
useful minterms, U as follows: U = M
1
∪ M
2
…;
where M
1
= M and M
i+1
= coalesce (M
i
, M).
□
The finite size of set of terms makes it easy to
see that for some finite k, M
k
= M
k+1
. To each u ∈ U
we associate precision(u) = |Relevant σ u|/
|Irrelevant σ u|; where denominator is 0, a large
value is assigned as precision.
A set of minterms where each minterm meets a
stipulated constraint precision value is a set of good
minterms. These minterms can be used to synthesise
query at the matching precision level. Formally,
Definition
GoodMinterms(U, p) = {u∈U | precision(u)≥ p &
∀w∈U [(u ⇒ w) ⇒ ((precision(w) < p)|(u≡w))]}
□
The precision values in set U are discrete; by
progressively lowering the value one can derive a
query that meets the search engine constraints at the
best precision value possible.
6 CONCLUDING REMARKS
The paper has described a method for constructing
search query from a collection of relevant and
irrelevant text documents. The method constructs the
query by following a series of stages. Each stage is a
greed-driven heuristic to certain goals. In our
experiments, we found the greedy approach to be
adequate; there is little need to seek optimised and
perfect Boolean expressions as there are
uncertainties outside our controls. For example, the
small number of documents used to construct the
query can only define a very imprecise image of
documents and resources on the Web. Efforts spent
on matching this imperfect image would not deliver
proportionate rewards.
The method performs well when a reasonable
collection of relevant and irrelevant documents is
available. As the size of the collection increases, it
becomes better image of the resources on the Web!
Too small a size of the set does not help in synthesis
of a good quality search query. A very large
collection, on the other hand, requires additional
processing effort. Particularly, it will require more
human effort to classify the documents in the
collection. The goal of the exercise is to reduce
human effort. A set of about 10 relevant documents
with 10 to 20 irrelevant documents are generally
adequate.
The constructed queries include some unintuitive
terms. However, the queries retrieve fresh links and
are precise when used over the Web. An unintuitive
term is one that web searchers are not likely use in
queries. An unintuitive term is not a counter-
intuitive term.
The tests that we have conducted using the
algorithm to this stage have shown very good
improvements in the quality of links to resources in
comparison with the links retrieved using naïve
queries. Even in the areas well understood by a user,
the synthesised queries have performed better than
those constructed by humans. Some performance
results are available in Patro and Malhotra (2005).
REFERENCES
Aho, A.V. and Ullman, J.D., 1992. Foundations of
computer science, Computer Science Press, New
York.
Apte, C., Damerau, F.J., and Weiss, S.M., 1994.
Automated Learning of Decision Rules for Text
Categorisation, ACM Transactions on Information
Systems, 3(12). 233-251.
Brin, S. and Page, L., 1998. The anatomy of a large-scale
hypertextual web search engine, J. Computer
Networks and ISDN Systems, 30(1). 107-117.
Patro, S. and Malhotra V. 2005, Characteristics of the
Boolean web search query: Estimating success from
characteristics, http://eprints.comp.utas.edu.au:81/
Sanchez, S.N., Triantaphyllou, E., Chen, J. and Liao,
T.W., 2002. An Incremental Learning Algorithm for
Constructing Boolean Functions from Positive and
Negative Examples, Computers and Operations
Research 29(12). 1677–1700.
Sebastiani, F. 2002. Machine learning in automated text
categorization, ACM Computing Surveys, 34(1): 1-47.
ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
296
