KNOWLEDGE ACQUISITION MODELING THROUGH DIALOGUE

BETWEEN COGNITIVE AGENTS

Mehdi Yousﬁ-Monod, Violaine Prince

LIRMM, UMR 5506

161 rue Ada, 34392 Montpellier Cedex 5, France

Keywords:

Intelligent agents dialogue, tutoring systems , logical reasoning.

Abstract:

The work described in this paper tackles learning and communication between cognitive artiﬁcial agents.

Focus is on dialogue as the only way for agents to acquire knowledge, as it often happens in natural situations.

Since this restriction has scarcely been studied as such in artiﬁcial intelligence (AI), until now, this research

aims at providing a dialogue model devoted to knowledge acquisition. It allows two agents, in a ’teacher’

- ’student’ relationship, to exchange information with a learning incentive (on behalf of the ’student’). The

article ﬁrst deﬁnes the nature of the addressed agents, the types of relation they maintain, and the structure and

contents of their knowledge base. It continues by describing the different aims of learning, their realization

and the solutions provided for problems encountered by agents. A general architecture is then established and

a comment on an a part of the theory implementation is given. Conclusion is about the achievements carried

out and the potential improvement of this work.

1 INTRODUCTION

This research aims at deﬁning a set of algorithms for

knowledge acquisition through dialogue between arti-

ﬁcial cognitive agents. By cognitive agents we mean

entities possessing knowledge as well as acquisition

and derivation modes. In other words, they are able

to capture knowledge externally, and to process and

modify it through reasoning. Moreover, agents are

characterized by one or several goals. As an artiﬁ-

cial intelligence (AI) entity, each agent owns a knowl-

edge base and attempts to make it evolve either by

environment observation (reactivity) or by derivation

modes (inductive or deductive reasoning). However,

human beings as natural cognitive agents favor dia-

logue as another mean for knowledge revision. This

mean tends to consider another agent as a knowledge

source, and then to proceed to derivation (by reason-

ing). Further, the knowledge source could be ad-

dressed in order to test wether the acquisition process

has succeeded. In a nutshell, this is what happens in

tutored learning.

To simulate learning we have chosen a socratic

dialogue (’teacher’ - ’student’) where knowledge is

presented exclusively by means of a question-answer

mode of interaction. The ’student’ agent owns belief

revision mechanisms and all axioms allowing formal

reasoning. Being in the modeling process, we wished

not to overload dialogue difﬁculties with language in-

trinsic ambiguity (i.e. pure “natural language” prob-

lems) and thus speciﬁed a “keleton protocol”: mes-

sage data will be exchanged in ﬁrst-order logic. How-

ever, this has been decided only to be able to focus

on dialogue particular features; we attempt, the best

we can, to make the dialogue situation as close to a

natural human-human dialogue between a ’teacher’

and a ’student’, as possible. We assume that agents

use a common formalism concerning terms, predi-

cates and functions. Nevertheless, the ’student’ agent

may not have predicates (or functions) given by the

’teacher’ agent and so can question it on this subject

before revising its base. In this paper, we try to show

how dialogue initiates reasoning, which leads to an

increase as well as a revision of the ’student’ knowl-

edge base according to hypotheses we simulate and

revision mechanisms we deﬁne.

201

Yousﬁ-Monod M. and Prince V. (2005).

KNOWLEDGE ACQUISITION MODELING THROUGH DIALOGUE BETWEEN COGNITIVE AGENTS.

In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 201-206

DOI: 10.5220/0002512002010206

 SciTePress

2 DIALOGUE AND LEARNING: A

BRIEF DESCRIPTION OF

RELATED LITERATURE

Several papers deal with human learning via dialogue

(DA 91). Those related to computer devices usu-

ally rely on human-machine dialogue models (Bak

94; Coo 00). However, for artiﬁcial agents only, the

very few papers about communication as an acquisi-

tion mode are in the framework of noncognitive envi-

ronment like robots (AMH 96) or noncognitive soft-

ware agents. It seems that, in artiﬁcial systems, learn-

ing is often realized without dialogue.

Learning without Dialogue. There are many kind of

learning methods for symbolic agents like reinforce-

ment learning, supervised learning (sometimes us-

ing communication as in (Mat 97)), without speaking

about neural networks models that are very far from

our domain. This type of learning prepares agents

for typical situations, whereas, a natural situation in

which dialogue inﬂuences knowledge acquisition, has

a great chance to be unique and not very predictable

(RP 00).

Dialogue Models. Most dialogue models in com-

puter science (namely in AI) are based on intentions

(AP 80; CL 92), rely on the Speech Act Theory (Aus

62; Sea 69), to deﬁne dialogue as a succession of

planned comunicative actions modifying implicated

agents’ mental state, thus emphasizing the importance

of plans (Pol 98). When agents are in a knowledge ac-

quisition or transfer situation, they have goals: teach

or learn a set of knowledge chunks. However, they

do not have predetermined plans: they react step by

step, according to the interlocutor’s answer. This is

why an opportunistic model of linguistic actions is

better than a planning model. Clearly, a tutored learn-

ing situation implies a ﬁnalized dialogue (aiming at

carrying out a task) as well as secondary exchanges

(precision, explanation, conﬁrmation and reformula-

tion requests can take place to validate a question or

an answer). We have chosen to assign functional roles

(FR) to speech acts since this method, described in

(SFP 98), allows unpredictable situations modelling,

and tries to compute an exchange as an adjusment be-

tween locutors mental states. We have adapted this

method, originally designed for human-machine dia-

logue, to artiﬁcial agents.

Reasoning. Reasoning, from a learning point of view,

is a knowledge derivation mode, included in agent

functionalities, or offered by the ’teacher’ agent. Rea-

soning modiﬁes the recipient agent state, through a set

of reasoning steps. Learning is considered as the re-

sult of a reasoning procedure over new facts or pred-

icates, that ends up in engulﬁng them in the agent

knowledge base. Thus, inspired from human behav-

ior, the described model acknowledges for three types

of reasoning: deduction, induction and abduction.

Currently, our system uses inductive and deductive

mechanisms. Abduction is not investigated as such,

since we consider dialogue as an abductive bootstrap

technique which, by presenting new knowledge, en-

ables knowledge addition or retraction and therefore

leads to knowledge revision (JJ 94; Pag 96).

Last, although our system is heavily inspired from

dialogue between humans and from human-machine

dialogue systems, it differs from them with respect to

the following items :

• Natural language is not used as such and a formal-

based language is prefered, in the tradition of lan-

guages such as KIF, that are thoroughly employed

in artiﬁcial agents communication. These formal

languages prevent problems that rise from the am-

biguity intrinsic to natural language.

• When one of the agents is human, then his/her

knowledge is opaque not only to his/her interlocu-

tor (here, the system) but also to the designer of the

system. Therefore, the designer must build, in his

system, a series of “guessing” strategies, that do not

necessarily fathom the interlocutor’s state of mind,

and might lead to failure in dialogue. Whereas,

when both agents are artiﬁcial, they are both trans-

parent to the designer, if not to each other. Thus,

the designer embeds, in both, tools for communi-

cation that are adapted to their knowledge level.

The designer might check, at any moment, the state

variables of both agents, a thing he cannot do with

a human.

These two restrictions tend to simplify the problem,

and more, to stick to the real core of the task, i.e.,

controlling acquisition through interaction.

3 THE THEORETICAL

FRAMEWORK

3.1 Agents Frame

Our environment focuses on a situation where two

cognitive artiﬁcial agents are present, and their sole

interaction is through dialogue. During this relation-

ship, an agent will play the role of a ’teacher’ and

the other will momentarily act as a ’student’. We as-

sume they will keep this status during the dialogue

session. Nevertheless, role assignation is temporary

because it depends on the task to achieve and on each

agent’s skills. The ’teacher’ agent must have the re-

quired skill to teach to the ’student’ agent, i.e., to offer

unknown and true knowledge, necessary for the ’stu-

dent’ to perform a given task. Conventionally, ’stu-

dent’ and ’teacher’ terms will be used to refer, respec-

tively, to the agents acting as such. The ’teacher’ aims

ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

202

at providing a set of predetermined knowledge to the

’student’. This, naturally subsumes that agents coop-

erate.

3.2 Knowledge Base Properties

Each agent owns a knowledge base (KB), structured

in ﬁrst-order logic, so the knowledge unit is a formula.

The ’student’ can make mistakes, i.e., possess wrong

knowledge. From an axiomatic point of view, if an

agent acts as a ’teacher’ in relation to a given knowl-

edge set, then the ’student’ will consider as true every

item provided by the ’teacher’.

Each KB is manually initiated, however, its update

will be automatic, thanks to ’learning’ and reasoning

abilities. In order to simplify modelling, we only use

formulas such sa (P ), (P → Q) and (P ↔ Q). (P )

and (Q) are predicates conjunctions (or their nega-

tion) of type (p(A)) or (p(X)) (or (not(p(A))) or

(not(p(X)))), where A = {a

, a

, . . . , a

} is a set

of terms and X = {x

, x

, . . . , x

} a set of vari-

ables. For simpliﬁcation sake, we note P and Q

such predicates conjunctions. Universal quantiﬁca-

tion is implicit for each formula having at least one

variable. We consider that, to initiate learning (from

the ’student’ position), the ’teacher’ has to rely on the

’student’s previous knowledge. This constraint imi-

tates humans’ learning methods. Therefore, before

performing a tutored learning dialogue, agents must

have a part of their knowledge identical (called ba-

sic common knowledge). The ’teacher’ will be able to

teach new knowledge by using the ’student”s already

known one. However, our agents do not ’physically’

share any knowledge (their KBs are independent).

Connexity as a KB Fundamental Property. Dur-

ing learning, each agent will attempt to make its KB

as “connex” as possible.

Deﬁnition 1. A KB is connex when its associated

graph is connex. A graph G

is associated to a KB Γ

as such:

Each formula is a node. An edge is created between

each couple of formulas having the same premise

or the same conclusion or when the premise of one

equals the conclusion of the other. For the mo-

ment, variables and terms are not took into account in

premise or conclusion comparison

. Thus, in a con-

nex KB, every knowledge element is linked to every

other, the path between them being more or less long.

As the dialogic situation must be as close as possi-

ble to a natural situation, agents’ KBs are not totally

An abductive reasoning mechanism is contemplated as

a possible mean to compare a constant fact q(a) with a pred-

icate with a variable q(y). We only consider the result of a

succeeding abduction.

connex: a human agent can often, but not always, link

two items of knowledge, haphazardly taken.

Examples:

A connex KB: Γ

= {t(z) ∧ p(x) → q(y),

r(x) → q(y), s(x) → r(y), q(a), r(b)}

A non connex KB: Γ

= {t(z) ∧ p(x) → q(y),

r(x) → q(y), s(x) → u(y), q(a), u(b)}

Deﬁnition 2. A connex component (or just compo-

nent) is a connex subset of formulas in a KB.

r(b)

s(x) r(y)

t(z) p(x) q(y)

q(a)

r(x) q(y)

(a) Γ

Associated Graph

t(z) p(x) q(y)

q(a)

s(x) u(y)

u(b)

r(x) q(y)

(b) Γ

Associated Graph

Figure 1: KB Associated Graphs

Figures 1(a) and 1(b) respectively represent graphs

associated to Γ

and Γ

Theorem 1. Let A, B and C be three connex for-

mulas sets. If A ∪ B and B ∪ C are connex then

A ∪ B ∪ C is connex.

Proof. Let us assume that A∪B and B∪C is connex

and G

, G

and G

are graphs respectively associ-

ated to A, B and C. According to deﬁnition 1: A ∪ B

connex is equivalent to G

∪G

connex. Also, B∪C

connex is equivalent to G

∪G

connex. And accord-

ing to connex graph properties: G

∪ G

connex and

∪ G

connex implies G

∪ G

connex. So

A ∪ B ∪ C is connex.

Agents will not attempt to increase the number of

their connex components. However, there will be

some cases where the ’student’ will be forced to do

so. Fortunately, in some other cases, learning new

knowledge may link two connex components into a

new larger one, decreasing the components total num-

ber (according to theorem 1).

KNOWLEDGE ACQUISITION MODELING THROUGH DIALOGUE BETWEEN COGNITIVE AGENTS

203

3.3 Dialogue: Using Functional

Roles (FR)

A dialogue session is the image of a lesson. The

’teacher’ must know what knowledge to teach to the

’student’: therefore, a lesson is composed of several

elements, each of them contained in a logic formula.

The teaching agent provides each formula to the ’stu-

dent’. However, before that, the teacher waits for the

’student”s understanding (or misunderstanding) mes-

sage of the last formula. If the ’student’ doesn’t un-

derstand or is not at ease, it can just inform its in-

terlocutor of the misunderstanding or, requests a par-

ticular information bit. The FR theory, that models

exchanges in this dialogue, allows the attachment of

a role to each utterance. Both agents, when receiving

a message, know its role and can provide an adequate

answer. We assign the type knowledge to universal or

existential general logical formulas and the type in-

formation to constant-uttering answer (or question):

i.e, which value is ’true’, ’false’, or ’unknown’. Here

are the main FR types used in the our tutored learning

dialogue.

1. give-knowledge. Used to teach a knowledge and

introduce an exchange, example:

give − knowledge(cat(x) → mortal(x)):

“Cats are mortal.”

2. askfor/give-information (boolean evaluation case) :

askfor-information. Example:

askfo r − information(cat(F olley)):

“Is Folley a cat?”

give-information

. Example:

give − inf ormation(true): “Yes.”

3. give-explanation

(predicate case). Example:

give − explanation(cat(x) ↔

(animal(x) and pet(x) )): “A cat is a pet animal.”

4. say-(dis)satisfaction

: tells the other agent that the

last provided data has (has not) been well under-

stood.

There are some FR we do not use (askfor −

knowledge, askfor−explanation, askfor/give−

example, askfor/give−precision, askfor/give−

reformulation) likewise some speciﬁc uses like the

type askf or/give − inf ormation in the case of an

evaluation by a function. So FR are dialogic clauses

allowing the interpretation of exchanged formulas. A

functional role of the“ask − f or” kind implies one or

a series of clauses of the “give” type, with the possi-

bility of using another “ask − f or” type if there is a

misunderstanding. This case will bring about a clause

without argument: “say − dissatisfaction”. Only

“ask − for” type roles will lead to interpretative ax-

ioms. Other ones are behavioral startings.

3.4 Tutored Learning

3.4.1 Axioms

Our reasoning system is hypothetical-deductive, so it

allows belief revision and dialogue is the mean by

which this revision is performed. Two groups of ax-

ioms are deﬁned: fundamental axioms of the system

and those corresponding to the FR interpretation in

the system. Each knowledge chunk of each agent is

seen as an assumption.

Fundamental axioms. Our system revision axioms

include the hypothetisation axiom, hypothesis addi-

tion and retraction, implication addition, implication

retraction or modus ponens and the

reductio ad absur-

dum rule

. These are extensively described in (Man

74).

FR interpretation axioms. Interpretation axioms are

not in the ﬁrst order since they introduce clauses and

multiple values (like the “unknown” one). Our syntax

will be in the ﬁrst order, but the interpretation is not

monotonous.

• give − knowledge(A) ⇒ A ⊢ T ;

any knowledge supplied by the teacher is consid-

ered as true.

• give − information(A) ≡ Aǫ[T, F, U ];

any supplied information is a formula interpretable

in a multi-valued space.

• give − explanation(A) ≡

(give − inf ormation(P ), A ↔ P );

any explanation consists in supplying a right for-

mula, equivalent to the formula A that has to be

explained.

With T for True, F for False and U for Unknown.

3.4.2 Tutored Learning Situations

Learning can have several goals like enriching the KB

with new data, increasing the KB connexity, widening

the predicates base, understanding why some formu-

las imply others. We mainly focus on the ﬁrst one

because of its importance. In order to learn, the ’stu-

dent’ must ﬁrst understand received data. By under-

standing, we mean “not increasing the KB compo-

nents number”: the ’student’ understands a data that

is linked to at least one component of its KB. By def-

inition, we consider that a ’student’ knows a predicate

if it owns it.

3.5 Dialogue Strategy

There are several dialogue strategies depending on the

goals chosen by the learner. In this paper, being lim-

ited in scope, we consider one goal: enriching the KB

with new data (while maintaining connexity as best as

ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

204

possible), because it is the commonest. Thus we sug-

gest the appropriate common strategy: solving a mis-

understanding problem by choosing adequate ques-

tions and answers. We have adopted a technique in-

spired from the socratic teaching method.

For each predicate p

to be taught, the ’teacher’ knows

another one p

linked with p

by an implication or

an equivalence F . Therefore, to ensure that the ’stu-

dent’ understands p

thanks to p

, he will have to ask

the ’student’ if the latter knows p

. If the ’student’

knows it, then the ’teacher’ only have to give F to the

’student’. Otherwise, the ’teacher’ will ﬁnd another

formula that explains p

and so on. Once data is un-

derstood, the ’student’ may realize that some bits are

contradictory with its KB, leading to a conﬂict.

Conﬂict Management. We have studied several

types of conﬂict, those related to implications as well

as those related to facts. In this paper, we will only

present the ﬁrst one, which typically takes place when

the ’student’ has a formula (P → Q) and attempts to

learn a formula (P → not(Q)). The solution, for

the ’student’, is removing (P → Q) from its KB and

adding (P → not(Q)). It acts so because we con-

sider that this is ’teacher”s knowledge (thus true)

and so it gets the upper hand on the ’student’ one

(ﬁrst axiom). However, the conﬂict could be hidden

if the ’student’ has the next formulas: (P

→ P

), ... , (P

n−1

→ P

) and attempts to learn

→ not(P

)): the ’student’ has an equivalent to

the formula (P

→ P

). Instead of using a base-

line solution consisting in removing all the series of

implications, we opted for a more ﬂexible one which

attempts to look for a wrong implication and only re-

move this one. Indeed, removing one implication is

sufﬁcient to solve the conﬂict. The ’student’ will then

attempt to validate each implication to the ’teacher’

through an “askf or − information” request. As

soon as a wrong implication is found, the ’student’

removes it and safely adds the new one. However, if

none of the implications is neither validated nor re-

jected by the ’teacher’, the ’student’ will be forced to

remove all the series before adding the new one to

be sure to end up the conﬂict. We have studied other

implication conﬂict types that are even less easily de-

tectable, but we have not a sufﬁcient space to detail

them.

4 SYSTEM ARCHITECTURE

AND IMPLEMENTATION

The theoretical approach of section 3 has been spec-

iﬁed and partially implemented. The speciﬁcation is

general, the implementation contains some of its ele-

ments presented in section 4.2.

4.1 Architecture

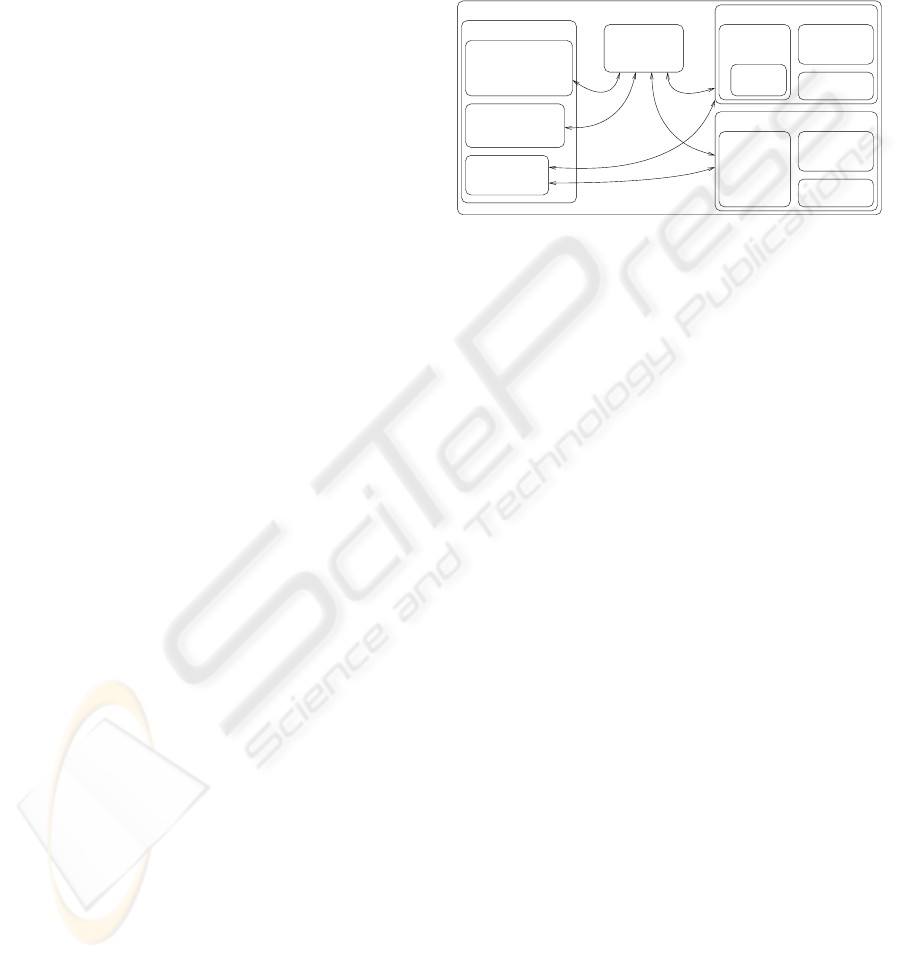
The ﬁgure 2 displays the main architecture elements

of our tutored learning system. It is composed of ﬁve

main structures: the ’teacher’, the ’student’, the FR,

the strategies and the ’World’. Each agent has a KB,

a model of itself and of its interlocutor. It can freely

...

Dialogue :

...

World

Strategies

Explain a predicate

Explain an implication

Local:

Conflicts management

Lessons :

Learning

Teaching

Student Agent

Knowledge

base

Knowledge

base

Lesson to

be taught

Teacher Agent

Model of oneself

Roles

Functional

Teacher’s Model

Student’s Model

Figure 2: The tutored learning system through dialogue be-

tween artiﬁcial cognitive agents

update them in order to make them evolve. It has an

access to strategies, for learning and teaching lessons

and to all the FR rules (seen in section 3.3).

4.2 Implementation

We have implemented a Java program to test conﬂict

solving. This programm is a basic prototype aiming

at getting experimental results of a part of our theory.

Each agent is an instance of the Thread Java class and

has a name, a knowledge base (KB) and a pointer to

• a World class (the environment at which it be-

longs),

• its possible teacher, student and interlocutor agents,

• the strategies class,

• the fonctional roles (FR) class.

The KB is made of two types of simple objects: facts

(a predicate name and a term) and implications (two

predicate names, two variables and a direction). An

exchanged message is one entry of the KB (a fact or

an implication) plus a FR type. Strategies are meth-

ods deﬁning sequential actions to perform in order

to accomplish the speciﬁc asked strategy. They can

be used directly by the agent (for lesson teaching for

example) or they can by called by their FR compo-

nent (for predicate explanation implied by a “say-

dissatisfaction” for example). The FR component is

a switch that routes the agent message to the good FR

method according to its FR type. Each FR method

uses the adequate strategies to satisfy agents.

Running the process shows that the ’student’ has

detected a conﬂict between its KB and a new data pro-

vided by the ’teacher’. He then asks the ’teacher’ to

KNOWLEDGE ACQUISITION MODELING THROUGH DIALOGUE BETWEEN COGNITIVE AGENTS

205

validate some potentially conﬂictual knowledge and

ﬁnally removes the wrong implication

5 CONCLUSION

Our system allows artiﬁcial cognitive agents, in a tu-

tored learning situation between a ’teacher’ and a ’stu-

dent’, to acquire new knowledge through sole dia-

logue. The study of such a constraint has led us to

deﬁne a notion of

connexity

for a knowledge base

(KB), allowing to assess the connection level be-

tween each element of knowledge of an agent and

so to give it a new goal: increasing its KB connex-

ity. As the dialogue situation in highly impredictable

and may follow no previous plan, we have adopted

the functional role theory to easily model dialogical

exchanges. Agents use strategies to learn new knowl-

edge and solve conﬂicts between external and internal

data. (Ang 88) tackles the problem of identifying an

unknown subset of hypothesis among a set by queries

to an oracle. Our work differs mainly in the commu-

nication mean: we use imbricated dialogues instead

of queries; and in the learning’s aim: our agents aim

at learning new formulas and increasing their KB con-

nexity instead of identifying hypothesis.

This work is a ﬁrst approach in learning by dia-

logue for cognitive artiﬁcial agents. Its aim is to de-

ﬁne a set of requirements for an advanced communi-

cation. Some paths could be explored like enriching

the KB content by new formula types or deﬁning new

dialogue strategies. Last, this type of learning could

be used in complement with others that rely on inter-

action with environment, in order to multiply knowl-

edge sources.

REFERENCES

D. Angluin: Queries and Concept Learning, Machine

Learning, Volume 2, Issue 4, ISSN:0885-6125,

Kluwer Academic Publishers, Hingham, MA, USA,

319-342, 1988.

H. Asoh, Y. Motomura, I. Hara, S. Akaho, S. Hayamizu, T.

Matsui: Acquiring a probabilistic map with dialogue-

based learning, In Hexmoor, H. and Meeden, L., ed-

itors, ROBOLEARN ’96: An Intern. Workshop on

Learning for Autonomous Robots, 11-18, 1996.

J. Allen, R. Perrault: Analyzing intention in utterances, Ar-

tiﬁcial Intelligence, 15(3), 143-178, 1980.

J.L. Austin: How to Do Things with Words, ed. J. O. Urm-

son and Marina Sbis, Cambridge, Mass: Harvard Uni-

versity Press, 1975.

Implementation details are reachable at

http : //www.lirmm.fr/ ∼ yousf i

M. Baker: A Model for Negotiation in Teaching-Learning

Dialogues, Journal of Artiﬁcial Intelligence in Educa-

tion, 5, (2), 199-254, 1994.

P. Cohen, H. Levesque: Intentions in Communication, Ra-

tional Interaction as the Basis for Communication.

Bradford Books, MIT Press, seconde dition, chap. 12,

1992.

J. Cook: Cooperative Problem-Seeking Dialogues in Learn-

ing, In G. Gauthier, C. Frasson and K. VanLehn (Eds.)

Intelligent Tutoring Systems: 5th International Con-

ference, ITS 2000 Montreal, Canada, June 2000 Pro-

ceedings, Berlin Heidelberg New York: Springer-

Verlag, 615-624, 2000.

S.W. Draper, A. Anderson: The Signiﬁcance of Dialogue

in Learning and Observing Learning, Computers and

Education, 17(1), 93-107, 1991.

J.R. Josephson, S.G. Josephson: Abductive Inference, Com-

putation, Philosophy, Technology, New York, Cam-

bridge University Press, 1994.

Z. Manna: Mathematical Theory of Computation, Interna-

tional ’student’ Edition. McGraw Hill Computer Sci-

ence Series, 1974.

M. Mataric: Using Communication to Reduce Locality in

Multi-Robot Learning, AAAI-97, Menlo Park, CA:

AAAI Press, 643-648, 1997.

M. Pagnucco: The Role of Abductive Reasoning Within the

Process of Belief Revision, Ph.D. thesis, University of

Sydney, 1996.

M. E. Pollack: Plan Generation, Plan Management, and

the Design of Computational Agents Proceedings of

the 3rd International Conference on Multi-Agent Sys-

tems, Paris, France, July, 1998.

A. Ravenscroft, R.M. Pilkington: Investigation by Design:

Developing Dialogue Models to Support Reasoning

and Conceptual Change, International Journal of Ar-

tiﬁcial Intelligence in Education, 11, (1), 273-298,

2000.

J. Searle: Speech Acts: An Essay in the Philosophy of

Language, Cambridge: Cambridge University Press,

1969.

G. Sabah, O. Ferret, V. Prince, A. Vilnat, S. Vosniadou, A.

Dimitrakopoulo, E. Papademetriou: What Dialogue

Analysis Can Tell About Teacher Strategies Related

to Representational Change, in Modelling Changes in

Understanding: Case Studies in Physical Reasoning,

Elsevier, Oxford., 1998.

ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

206