MODELS’ SPECIFICATIONS TO BUILD ADAPTATIVE MENUS
Gérard Kubryk
Laboratoire I3S/CNRS in Sophia Antipolis
Keywords: Web and audio services, requirements analysis, adaptative and customized menus, models and methods
specifications, machine learning
.
Abstract: Web engineering becomes increasingly important in the last years. WEB and audio services have to provide
the best services possible. To achieve this goal, they have to find out what the customers are doing without
altering their privacy. This paper presents two classes of models, mathematical and learning models, and
two possible ways to manage and build adaptative menus. These methods are gravity analogy, learning by
sanction reinforcement. Later on, a comparison of these two models will be made based on two criteria:
efficiency (answering time and computer load) and accuracy with customer expectation. The final step will
be to carry out psychological analysis of user activity, meaning, “what is my perception of time into and
between service consultation” to determine ways to set parameters of such a system.
1 INTRODUCTION
When a customer is accessing a WEB site or uses a
value added service, he wants to have efficient
access whereby he can access information as quickly
as possible. One way to achieve this goal is to
remember what the user has previously done and
then to offer him (in real time) a menu or an access
organization suited perfectly to his preferences
without wasting time.
Finally, for effective marketing analysis, a company
needs to know where the services are located in their
own life curve. Characterization of a customer’s
action uses age of action, length, repetitions and
time period of these repetitions. We have to ensure
user privacy and the way this information is stored.
We also have to maintain the possibility for new
services to be created and presented.
2 THE MODELS
2.1 Mathematic analysis
The problem we have to solve is an organization
problem that allows managing time on the way users
access WEB pages or data. So we need information
that we could organize like a vector to allow the
system to compute the best menu (Fig 1):
User ID
Theme
ID
these two parts are keys to access the
right vector
Date
/hour
allows all calculations
f(t)
this values is the function of time used to
calculate rank of the theme for the user
f’(t)
the derivative of the above function (the
slope of the curve) is a way to analyze the
status of the theme for the user:
- If it’s positive, high gradient slope, we
are in a period of a user’s strong interest
- If it’s positive or negative, a low
gradient slope, the user’s interest is
reducing
- If it’s negative high gradient slope, we
are in a period of a user’s poor interest
Figure 1: Vector of useful information
The system has to create a vector for each user each
time a theme is accessed.
All theme vectors for a
given user give the organization of the best possible
menu when the user re-enters the service.
X
i
f(t)
theme organization
(we define f(t) as the function allowing the
modification of
X
i
according to the time elapsed
between two accesses)
168
Kubryk G. (2005).
MODELS’ SPECIFICATIONS TO BUILD ADAPTATIVE MENUS.
In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 168-171
DOI: 10.5220/0002513201680171
Copyright
c
 SciTePress

Vector
X
i
could have two forms according to the
fact that we could have one vector for each event
(n vectors for each theme) or only one if we make a
calculation of this vector for each access (1 vector
for each theme).
In all cases, vectors must include the following
components :
• User ID
• URL or theme ID
• Time and date of event
• Duration of event
In “1 for each theme” method, we need to add the
last two components which are:
• f(t) at event time
• f’(t) at event time
This means that at each event for a “user – theme”
couple, an f(t) and an f’(t) are evaluated.
Vectors
X
i
are:
N for each theme
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
duration
hour / date
ID Theme
Id User
1 for each theme
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
(t)f'
f(t)
duration
hour / date
Id Theme
Id User
The choice between the two forms has a strong
effect on the way the system responds. In the case “n
for each theme” we have to recalculate all the strings
of events to get the final altitude and the final speed.
This could take a very long time and this time
increase at each new consultation. Therefore, we
think that the solution “1 for each theme” is more
efficient.
It is also clear (the computation is not reversible)
that “1 for each theme” allows a full guarantee of
user privacy as it is impossible to go back and get
information about previous users’ accesses.
We could use the same method to analyze a theme
or a URL. In this case, the vector becomes
:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
(t)f'
f(t)
duration
hour / date
Id Theme
There is no “user ID” as the user has no meaning in
this case. Thus, it becomes very easy (in the same
way as described above) for a provider to have a real
time analysis for a product or a theme, to know
where it is in its life’s curve, and to act on them
accordingly.
2.2 The gravity analogy
One possible f(t) function could be gravity. Gravity
is a very useful way to organize the different themes
of a WEB site. We will show that, according to user
activity, we will get a different altitude that could
suit what we are looking for. It’s also very easy to
modify parameters to have a slightly different result.
We use very basic physical laws:
• Information is defined like a “Quantum” with a
masse “M”.
• This masse receives an amount of energy and
gains a vertical speed according to the following
laws:
E =
2
1
m v
2
V
0
=
m
2
1
Ε
0
(speed equation)
P(t) = V
0
t - ½ g t
2
(altitude equation)
• Speed evolution:
V(t) = V
0
- g t
• Maximum altitude
P
m
is:
P
m
= ½
g
V
2
0
In this case, speed equation becomes:
V
r
(t) = V
0
+ V
1
-
g t
And altitude equation is :
P
r
(t) = V
0
t - ½ g t
2
+ V
1
(t
-
t
1
)
Moreover, for n quanta of energy we have for speed:
V(t) =
∑
V
=
n
0i
i
- g t
And for altitude:
P(t) =
∑
V
=
n
0i
i
(t - t
i
) - ½ g t
2
One very important consequence is that values of V
i
must be chosen in such a way that we do not have
values decreasing whatever the user activity is.
2.3 Learning analysis
Learning is another way to define the right position
of items in a menu. Different ways to introduce
learning processes into computers have been
imagined over many years. Psychology defines
processes that interact with humans and animals to
create a new aptitude, as learning. This learning
could be done in different ways. One of them is
learning by a reinforcement process which means
that a rewarded action is strengthened (becomes
more probable) and a non-rewarded action is
weakened (becomes less probable). This
reinforcement is tempered by both habit (when the
MODELS’ SPECIFICATIONS TO BUILD ADAPTATIVE MENUS
169

result is always close of the expected one), and by
surprise (when there is a very unexpected one).
Surprise increases learning.
Habituation decreases learning.
Base of proposed system is rank of item selected
by user at time « t ». These ranks are in natural order
from rank 1 to rank “n”, n is only limited by screen
used like refrence by the menu designer and by
readability rules. This means that rank difference is
negative when user goes from rank « n » toward
rank 1. What we need to know in our sytem is
previous prediction, previous user choice, difference
between them, and time difference between the two
last choices. The general formula is then:
So surprise and habituation are the 2 sides of the
same parameter named K
sa
. We say that there is
habituation when difference between predicted rank
and real rank is less than « X » and surprise when
difference is greater than « X ». (∆ > X surprise ; ∆
< X habituation ; ∆=X indifférence).
By convention factor K
sa
values are between 0 and 2
accordingtofollowing rules: 0>K
sa
>1habituation ;
K
sa
= 1 indifference ; 1 > K
sa
> 2 surprise.
P
n
= g(P
n-1
, Choice
n-1
, ∆, ∆
t
)
Reinforcement is a function of 1/ ∆
t
. A short period
between two accesses to an item means an interest to
it, we have to manage it in our formula, reinforce
system answer and increase rank of this item. We
name this parameter K
r
.
In this formula :
P = the system prediction
Choice = rank of the item selected by the user
∆ = difference between previous prediction and
the user’s choice (P
n-1
- Choice
n-1
)
The factor p(K
f
)( ∆, ∆
t
) that we name sanction takes
the following form : p(K
f
)( K
sa
∆ + K
r
∆ / ∆
t
)
∆
t
= difference between time of the last accesses
and after extraction of the common factor :
g is the function that links up these factors
The first parameter is forgetfulness (Kf). This
parameter defined how system forgets prediction.
This mean that if Kf decreases (increase
forgetfulness), user’s choice get a lot of weight. Our
formula then becomes:
p(K
f
) ∆ ( K
sa
+ K
r
/ ∆
t
)
The complet formula is:
P
n
= K
f
P
n-1
+ (1 - K
f
)Choice
n-1
+p(K
f
) ∆( K
sa
+ K
r
/ ∆
t
)
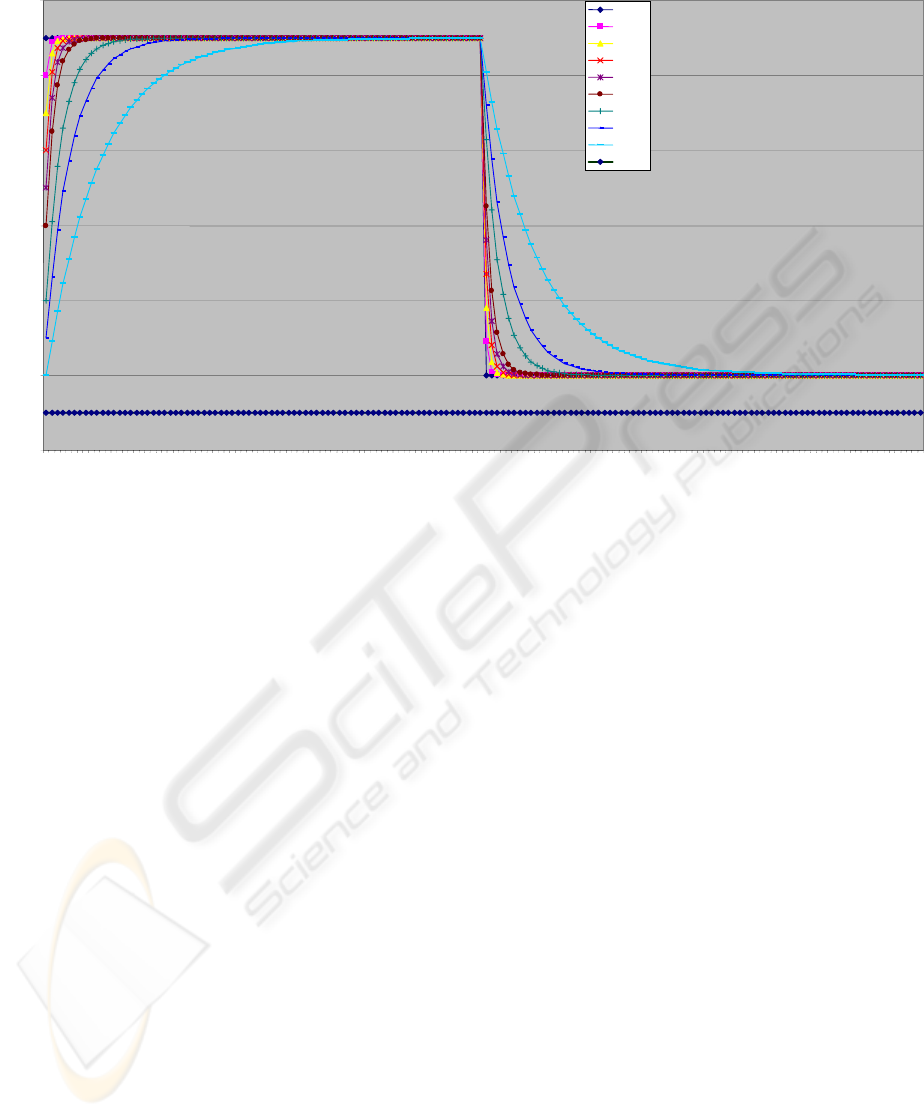
Our first simulations of the way Kf is acting gives
the following curves (Fig 2).
P
n
= K
f
P
n-1
+ (1 - K
f
)Choix
n-1
+ f( ∆, ∆
t
)
K
f
is acting in the following way :
K
f
=0 (maximum forgetfulness)
3 CONCLUSION
P
n
= Choice
n-1
+ f( ∆, ∆
t
)
System has forgotten its previous predictions and
only user’s choice modify prediction. This is
tempered by the factor f( ∆, ∆
t
).
We have now to make a full comparison of these
different models. This comparison must be based on
efficiency (time needed to respond, load on
computer, etc.) and accuracy of results. The second
step is to check psychological accuracy of the
chosen algorithm. This second step is also necessary
to define the right parameters of the chosen
algorithm and the meaning of these parameters.
K
f
=1 (no forgetfulness) : P
n
= P
n-1
+ f( ∆, ∆
t
)
System does not forget and cannot evoluate
according to user’s choice. This is tempered by the
factor f( ∆, ∆
t
).
In order to get perfect forgetfulness we need that f(
∆, ∆
t
) could also be a factor equal to 0 when Kf = 0
and when Kf = 1. This means that “f” is a curve
p(K
f
) to be defined that cut “X” axis for these 2
values. This means :
The main questions we are thinking about at this
time are:
• Is it acceptable by users to get a modified menu,
even if it is to put what they prefer at the top?
What is the risk of confusing users in this case?
How far could be the new position of an item
versus the previous one?
If K
f
= 0 then P
n
= Choice
n-1
System has completely forgotten predictions and
only user’s choice modify prediction.
• What is expected by the user regarding the
memorization of the past by the system. This
expectation must be fulfilled to satisfy the
customer.
If K
f
= 1 P
n
= P
n-1
System does not forget and cannot know evolution
according to user’s choice.
The general formula becomes :
• What is the meaning for the user of time spent
on the service. Must we increase the level of the
item according to time elapsed on the item or
give no meaning to it ?
P
n
= K
f
P
n-1
+ (1 - K
f
)Choice
n-1
+ p(K
f
)( ∆, ∆
t
)
We need now to introduce 3 more parameters first
one is surprise, the second one habituation, the last
one is reinforcement.
These factors are described by p(K
f
)( ∆, ∆
t
)
ICEIS 2005 - HUMAN-COMPUTER INTERACTION
170

• What is the meaning for the user of its
consultation period. Is importance for the user
proportional to inverse of this period ?
• What is the meaning for the user of the time
elapsed since previous consultations
• What are the laws followed by time perception.
Is it linear or is it following another law
exponential, logarithmic or a law to be found ?
• What is the value of consultation of close
themes. Must we increase levels of all the close
themes or consider that each theme is
independent ?
• What is the value of consultation of far theme.
Must we decrease levels of all the far themes or
consider that each theme is independent ?
• What is the value of preferences given at
registration by the user ?
• Do we have to give a different measure to
action according to the:
- hour in the day of user activity
- day of the week
- longer period
REFERENCES
R. Baron, M.B. Gordon, H. Paugam-Moisy, et al. , 1996.
Comparative study of three connectionist models on a
classification problem.In Ecole Normale Supérieur de
Lyon Laboratoire de l’informatique du Parralélisme,
Research report.
P Collard , 1992. L’apprentissage discriminant dans
MAGE. In Nice University / HDR.
Alessio Gaspar, Philippe Collard, 2000
Immune
Approaches to Experience Acquisition in Time
Dependent Optimization. In
Artificial Immune
Systems, Las Vegas, Pages 49-50,
Alessio Gaspar, Philippe Collard
, 2000. Two Models of
Immunization for Time Dependent Optimization.
Jones, Smith and Löf, 1998. Measurement and analysis of
Evaporation from Swimming Pool in active use. In
American Society of Heating, Refrigeration and Air
Conditionning Engineers Transactions 1998 V 104
Research #4146, pg 514 Atlanta.
M. Perkowitz ans O. Etzioni, 1998. Adaptative Web
Sites : Automatically synthetizing Web pages. In
Proceeding of the fifteen National Conference on
Artificial Intelligence.
M. Perkowitz ans O. Etzioni. Adaptative Sites :
Automatically learning from User access patterns. In
University of Washington, Department of Computer
Science, Internal report.
Marlène Villanova-Oliver, Jérôme Gensel, Hervé Martin,
2002. Progressive Access : A step toward adaptability
in Web-based informations sytems. In OOIS 2002,
LNCS 2425, 422-433.
Figure 2: Learning for different values of Kf.
-1
1
3
5
7
9
11
1 5 9
13 17 21 25 29 33 37
41 45 49 53 57 61 65 69 73 77 81
85 89 93 97
101 105 109
113
117 121 125 129 133
137 141 145 149 153
Temps
Rang
kf = 0
kf = 0,1
kf = 0,2
kf = 0,3
kf = 0,4
kf = 0,5
kf = 0,7
kf = 0,8
kf = 0,9
kf = 1
MODELS’ SPECIFICATIONS TO BUILD ADAPTATIVE MENUS
171