AUTOJOIN: PROVIDING FREEDOM FROM SPECIFYING JOINS

Terrence Mason

Iowa Database and Emerging Applications Laboratory, Computer Science

University of Iowa

Lixin Wang

Iowa Database and Emerging Applications Laboratory

University of Iowa

Ramon Lawrence

Iowa Database and Emerging Applications Laboratory, Computer Science

University of Iowa

Keywords:

Inference, Query, Interface, Schema, Ambiguity, Database.

Abstract:

SQL is not appropriate for casual users as it requires understanding relational schemas and how to construct

joins. Many new query interfaces insulate users from the logical structure of the database, but they require

the automatic discovery of valid joins. Although speciﬁc query interfaces implement join determination algo-

rithms, they are tied to the speciﬁc language and typically limited in scope or scalability. AutoJoin provides a

general solution to the query inference problem, which allows more complex queries to be executed on larger

and more complicated schemas. It enumerates query interpretations at least an order of magnitude faster than

previous methods. In addition, the engine reduces the number of queries considered ambiguous. Experimen-

tal results demonstrate that query inference can be efﬁciently performed on large, complex schemas allowing

simpler access to databases through keyword search or conceptual query languages. AutoJoin also provides

programmers with a tool to iteratively create SQL queries without requiring explicit knowledge of the structure

of a database.

1 INTRODUCTION

Despite signiﬁcant improvement in the performance

of database systems, the usability of databases has

not improved at a similar pace. Although more us-

able query interfaces, including conceptual, graphi-

cal, and keyword languages, have been developed,

they require the automatic determination of joins to

complete the queries. The lack of a consistent join de-

termination approach, which scales to large schemas,

continues to limit the capabilities of new query inter-

faces. Even worse, the size and complexity of data-

base schemas continues to grow, especially as global

schemas are constructed for integrated systems. Users

need a simpler method for querying larger and more

complicated databases.

One of the major challenges in generating SQL

queries is using joins to connect concepts or attributes

located in different tables. Constructing these joins in

SQL or through a graphical query interface is tedious,

error-prone, and not intuitive to casual users (Catarci,

2000). Recent research using keyword searches on

relational databases (Hristidis and Papakonstantinou,

2002; Balmin et al., 2004; Agrawal et al., 2002)

allows the extraction of data without any required

knowledge about the schema or metadata. These

interfaces match keywords either to the data or the

metadata of a database, which then requires the deter-

mination of the joins to relate the relations containing

the keywords.

Our goal is to produce a query inference engine that

dynamically converts an attribute-only or keyword

query to SQL. For example, consider the equivalent

keyword, conceptual and SQL queries on the TPC-H

schema shown in Figure 1. It is desirable for the query

system to automatically infer the SQL query from the

simpler keyword and conceptual queries. This allows

the creation of SQL queries without requiring explicit

knowledge of the database.

The challenge is to make query inference efﬁcient,

general, and practical for use in production databases.

The query inference system should be query language

independent to not restrict join determination to a par-

ticular query language. It also is critical that the over-

head of query inference be minimal even for very

large schemas.

Although ambiguity cannot be eliminated by a

query inference strategy (since it is inherent in the

http://www.tpc.org/tpch/

Mason T., Wang L. and Lawrence R. (2005).

AUTOJOIN: PROVIDING FREEDOM FROM SPECIFYING JOINS.

In Proceedings of the Seventh Inter national Conference on Enterprise Information Systems, pages 31-38

DOI: 10.5220/0002516100310038

 SciTePress

Keyword Query:

Part ‘United States’

Conceptual Query:

select Part.Name

where Nation.Name = ‘United States’

SQL Query:

select P.name

from part P, nation N, lineitem LI,

orders O, customer C

where N.name = ‘United States’

and P.partkey = LI.partkey

and O.custkey = C.custkey

and C.nationkey = N.nationkey

and LI.orderkey = O.orderkey

Figure 1: Equivalent Keyword, Conceptual, and Inferred

SQL Queries on TPC-H

relational schema), approaches to recognize and deal

with ambiguity are necessary to make query inference

valuable. Two speciﬁc forms of ambiguity that may

lead to multiple query interpretations are addressed.

In addition, schemas may have multiple sets of joins

that are equivalent in their semantic meaning. By

identifying and reducing these duplicate join paths to

a single core path, ambiguity is reduced.

The AutoJoin inference engine efﬁciently ex-

tends the capabilities of previous inference ap-

proaches, while maintaining independence from par-

ticular query languages or interfaces. The individual

contributions of AutoJoin are:

• An algorithm called EMO that efﬁciently con-

structs all maximal sets of lossless joins in a

schema. EMO signiﬁcantly outperforms previous

approaches that fail on large schemas.

• A method for reducing the number of ambiguous

queries by detecting and removing semantically

equivalent interpretations.

• Efﬁcient algorithms for generating query interpre-

tations at query execution time.

• An extension of the lossless join approach to gen-

erate queries with a lossy join.

• A performance study that demonstrates the ap-

proach is scalable.

The rest of this paper is organized as follows. Sec-

tion 2 provides background on query inference strate-

gies. Section 3 presents the AutoJoin inference en-

gine along with the join graph structure. Section 4 de-

scribes the overall strategy for precomputing the loss-

less join trees by the EMO algorithm. Efﬁcient join

determination algorithms are presented in Section 5.

A performance study in Section 6 shows that query

inference can be performed with minimal overhead

even for large schemas. The paper then closes with

future work and conclusions.

2 BACKGROUND

State of the art database interfaces require query in-

ference, as users should not be required to know the

schema and structure of the database queried. Key-

word searches along with natural language query-

ing require an efﬁcient, scalable, and general strat-

egy to discover joins for query execution . An ideal

query inference engine would automatically apply to

existing relational schemas without administrator in-

tervention, quickly pre-compute the necessary data

structures to minimize overhead during query execu-

tion, and return a ranked list of query interpretations

based on speciﬁcations from the query interface.

The Universal Relation provided the ﬁrst interface

which required query inference. The lossless join

property related to functional dependencies provided

the mechanism to determine the joins required to

complete the query (Maier and Ullman, 1983). If

more than one lossless interpretation exists, the in-

ferred query results in the union of all the unique loss-

less queries. In another approach, the query with the

lowest cost (Wald and Sorenson, 1984) is selected as

the inferred query. The cost function ﬁrst identiﬁes

a lossless interpretation. If lossless joins do not ex-

ist for the query, lossy joins are permitted. These two

approaches both infer a single query, while new inter-

faces require a ranked list of interpretations.

The pursuit of simpler interfaces for relational data-

bases has led to varying methods of join determina-

tion. Each keyword search interface has developed

their own algorithm to address the challenges of ﬁnd-

ing the k-lowest cost query interpretations for a set of

keywords. Discover (Hristidis and Papakonstantinou,

2002) grows all ways from a relation containing one

of the keywords with a limit on the number of joins

permitted between relations. This inefﬁciently gener-

ates extra graphs that do not contain all the keywords.

DBXplorer (Agrawal et al., 2002) identiﬁes the lo-

cation of keywords through an efﬁcient symbol table

and then infers the joins required for query interpreta-

tions by generating spanning trees. Neither approach

maintains the lossless property in their cost functions

and all computations occur at query time.

Conceptual query languages aim to hide the com-

plexity of the schema from users by mapping con-

cepts familiar to the user to the relational model.

Again, these languages require the identiﬁcation of

joins to complete the query. CQL (Owei and Navathe,

2001) uses a shortest path algorithm to ﬁnd the mini-

mum join paths between speciﬁed concepts resulting

ICEIS 2005 - HUMAN-COMPUTER INTERACTION

in a single query interpretation. Another conceptual

model (Zhang et al., 1999) requires an administrator

to semi-automatically generate and annotate a seman-

tic graph of the database and then uses a search al-

gorithm constrained by limiting both the number of

joins and interpretations generated. Natural language

interfaces (Popescu et al., 2003) map a natural lan-

guage query to concepts represented in the database,

then the joins required to connect all concepts must

be determined.

Obviously, query inference is critical to the devel-

opment of advanced user interfaces. However, each

inference system directly links their join determina-

tion algorithms to a speciﬁc query interface with a

hard-coded mapping algorithm to generate the SQL

query. These solutions are inherently not conﬁg-

urable. The goal is to isolate query inference at the

schema level away from the query interface, to focus

on the overall challenges of query inference. By solv-

ing the query inference problem in general, the Auto-

Join inference engine will allow the development of

query interfaces without the constraint of a speciﬁc

join determination algorithm.

3 ARCHITECTURE

The AutoJoin architecture consists of a pre-

processing step to identify maximal lossless joins

and a query-time inference engine to determine joins

for the query interface. In the pre-processing step,

schema information is extracted from relational data-

bases using standard API calls and stored in a generic

schema representation called a join graph. The at-

tributes and relations are optionally annotated to im-

prove names and reduce ambiguity. Next, the sys-

tem computes the maximal lossless joins and stores

all information into an XML document for future

QueryBuilder loads.

The query interface (see Figure 2) may be any text

language or graphical query tool. The query inter-

face allows the user to enter queries and then trans-

lates the user’s query into a set of nodes and edges on

the join graph. Nodes represent relations and edges

represent joins. The query interface may provide a

cost function, mapping costs to edges and nodes to

rank the interpretations. The QueryBuilder takes

this information and uses the pre-computed informa-

tion to enumerate the potential interpretations. The

Generator constructs all interpretations and passes

them to the Ranker which uses any supplied rank-

ing function to order the interpretations. Finally, the

query interface uses the Iterator to return the in-

terpretations in rank order. The query interface then

executes the queries on the database. Since the ar-

chitecture only requires the query interface to specify

Document

XML

Iterator

Loader

RankerGenerator

QueryBuilder

Query Interface

User

Database

Relational

Interpretations

Inference Request

AutoJoin QI Engine

(interpretations)

Execute queries

Figure 2: AutoJoin Architecture

the nodes of interest, the query interface has complete

control over the inference process. The key compo-

nents of the architecture are discussed in the follow-

ing sections.

3.1 Representing Joins of a Schema

The potential joins in a relational schema are repre-

sented by a directed graph called a join graph.

Deﬁnition 1 A join graph JG = (N, E) for rela-

tional database schema S is a directed graph where:

• Each relational schema R

∈ S is represented as a

node n

∈ N .

• There is a directed edge e = (n

, n

) ∈ E from

node n

(relation R

) to node n

(relation R

) if

there exists a foreign key constraint of the form

[A] ⊆ R

[B] where A and B are subsets of the

attributes of R

and R

respectively.

A join graph can be automatically built from an ex-

isting relational schema by extracting relation names

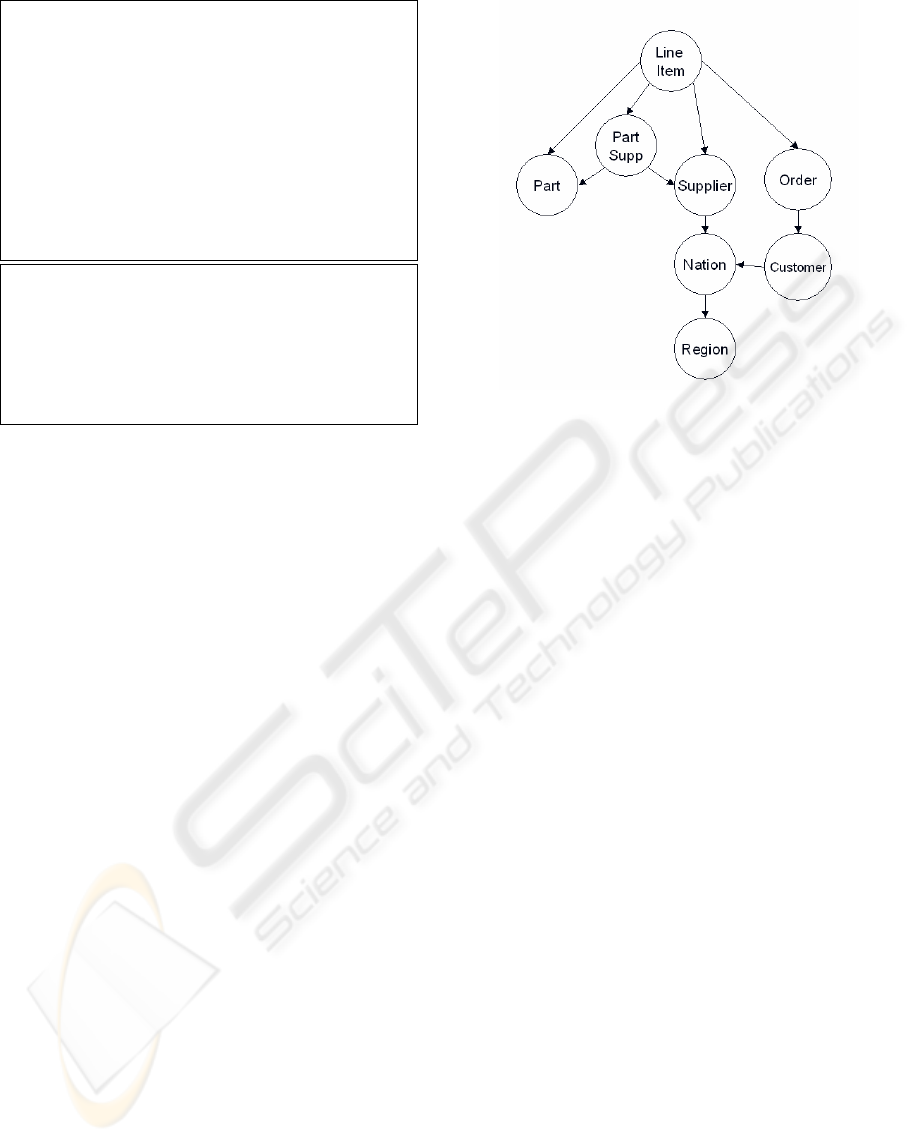
and foreign key constraints. The example TPC-H

schema used throughout this paper is in Figure 3, and

its associated join graph is in Figure 4. Joins may be

added to the join graph to identify additional potential

joins. It is possible to have multiple edges between

two nodes if there are two or more foreign keys be-

tween them. Determining the maximal set of lossless

joins reduces to the problem of ﬁnding all connected,

maximal subtrees of the join graph, as the lossless

property is captured in the direction of the edges.

We now formally deﬁne the meaning of a query,

query interpretation, and query inference.

AUTOJOIN: PROVIDING FREEDOM FROM SPECIFYING JOINS

part(partkey, name, mfgr, brand, type, size,

container, retailprice, comment)

supplier(supkey, name, address, nationkey, phone,

acctbal, comment)

partsupp(partkey,supkey,availqty,supcost)

customer(custkey,name,address,nationkey,phone,

acctbal, mktsegment,comment)

orders(orderkey, custkey, status, totalprice, orderdate,

priority, clerk, shippriority, comment)

lineitem(orderkey, partkey, supkey, linenumber, qty,

extendprice, discount, status, shipdate)

nation(nationkey, name, regionkey, comment)

region(regionkey, name, comment)

lineitem(partkey)⊆partsupp(partkey)⊆part(partkey)

lineitem(supkey)⊆partsupp(supkey)⊆supplier(supkey)

lineitem(partkey,supkey)⊆partsupp(partkey,supkey)

orders(custkey)⊆customer(custkey)

customer(nationkey)⊆nation(nationkey)

supplier(nationkey)⊆nation(nationkey)

lineitem(orderkey)⊆orders(orderkey)

nation(regionkey)⊆region(regionkey)

Figure 3: Abbreviated TPC-H Schema

Deﬁnition 2 A user query Q = (N

′

, E

′

) on a join

graph J G = (N, E) is a subgraph of J G such that

′

⊆ N and E

′

⊆ E.

For use in query inference, a user query reduces

to a set of speciﬁed nodes (relations) and edges (nat-

ural joins). A node is speciﬁed if one or more of its

attributes are required for a selection, projection, or-

dering, or grouping operation. A speciﬁed edge is a

natural join condition explicitly given by the user. The

query interface must translate the user query into the

required form.

Deﬁnition 3 A query interpretation QI = (N

′

, E

′

)

on a join graph JG = (N, E) is a connected sub-

graph of JG such that N

′

⊆ N and E

′

⊆ E.

A query interpretation is usually a tree, but may be

a graph. We use the terms join tree to represent loss-

less joins and lossy join interpretation for query in-

terpretations that include a lossy join. An ambiguous

query has multiple join trees. A query may be unam-

biguous (single join tree) even if the schema contains

ambiguity.

Deﬁnition 4 The query inference problem requires

enumerating and ranking query interpretations of a

query such that the query interpretation desired by the

user is among the highest ranked interpretations.

Previously, query inference was deﬁned as select-

ing a single interpretation for the user. This is im-

practical because a system will never be able to se-

lect the correct interpretation for every situation. We

re-formulate the query inference problem as an infor-

mation retrieval problem. The goal of query infer-

ence is to enumerate potential query interpretations

Figure 4: Join Graph for TPC-H Database

and present them to the user in order of the likelihood

that the interpretation is what the user intends. This

is similar to how a web search engine ranks pages

according to the expected value for the user. Query

inference then becomes two related problems. First,

given a subset of nodes and edges of the join graph,

the system must enumerate the possible connections

between them. Then, it will rank the interpretations

based on the speciﬁed cost function.

4 PRECOMPUTING LOSSLESS

JOINS

As the maximal sets of lossless joins depend solely on

the ambiguity inherent in the schema and not on the

input of a speciﬁc query, the maximal sets of lossless

joins for the schema are precomputed. This moves the

bulk of the computation from query time to a one time

precomputation. If there is no ambiguity in a schema,

then query inference is trivial with only one possible

interpretation for any query. AutoJoin is designed to

infer queries on schemas with ambiguity. There are

two common sources of ambiguity in schemas:

• A single relation storing an entity that plays mul-

tiple roles results in a node in the join graph with

two or more incoming edges.

• Multiple semantic relationships between entities

result in directed cycles and strongly connected

components in the join graph.

The ﬁrst source of ambiguity is common as

schemas have shared lookup tables used by multiple

relations. An example in TPC-H is Nation that serves

ICEIS 2005 - HUMAN-COMPUTER INTERACTION

the two semantic roles of storing the nation of cus-

tomers and the nation of suppliers. This form of am-

biguity arises when distinct attributes have the same

underlying domain of values. An example of the sec-

ond source of ambiguity is a database storing employ-

ees and departments where an employee has a depart-

ment and a department has a manager (which is also

an employee). These two relationships result in a di-

rected cycle between employee and department in the

join graph. The number of query interpretations is

dictated by the ambiguity inherent in the schema.

4.1 Removing Shortcut Joins

Semantically equivalent query interpretations with

distinct sets of joins may exist in a database schema.

It is critical that these equivalent joins be detected

and only the core semantic join path preserved in the

join graph, otherwise queries may be incorrectly de-

termined to be ambiguous. A shortcut join is a join

between two relations that is semantically equivalent

to a longer join path of two or more edges. This is

especially common in hierarchically structured data-

bases where the primary key of one relation contains

the primary key of its parent relation. We denote a

natural join on foreign key attributes X between two

relations R

and R

as R

⊲⊳

. To simplify the

discussion, the set of attributes X is assumed to have

the same name in both relations, although in practice

this is not required.

Deﬁnition 5 A shortcut join between two relations R

and R

is a natural join on attributes X where X ⊆

and X ⊆ R

and there exists a join path R

⊲⊳

... ⊲⊳

⊲⊳

where Z = X

and Z ⊆ X

⊆ X

n−1

... ⊆ X

A shortcut join is equivalent to the longer join path

based on functional dependencies. The functional de-

pendency R

[X] → R

of the shortcut join is equiv-

alent to R

[Y ] → T [Z] → R

since X ⊆ Y and

Z = X. Shortcut joins can be detected while build-

ing the join graph. If a relation R

has two foreign

keys on sets of attributes Y and X to relations R

and

respectively, where X ⊂ Y then the join from R

to R

on X is a shortcut join and is not added to the

join graph. Shortcut joins are maintained in a list and

are re-inserted at query-time when the shortcut join

can be used to reduce query execution times.

There are two shortcut joins in the TPC-H schema:

LineItem to Part and LineItem to Supplier. By remov-

ing these joins, the number of maximal join trees in

Figure 5 is reduced from 8 to 2 (join trees 1 and 5),

and the number of unambiguous queries increases to

26% from 8% (Figure 8). At query-time, if a query

speciﬁes only LineItem and Part, the path in the max-

imal join tree will be: LineItem-PartSupp-Part which

Figure 5: Maximal Join Trees for TPC-H Database

is replaced by the shortcut join LineItem-Part, as Part-

Supp is not required in the query.

4.2 Generating Maximal Join Trees

Previous approaches for generating maximal sets of

lossless joins (join trees) expanded in all possible di-

rections. The growing algorithm was inefﬁcient, and

often non-computable, for large graphs. Our approach

constructs the sets of joins without expanding in all

possible ways by growing maximal join trees only

from identiﬁed roots. Since lossless joins are trees,

a root of a join tree cannot be a node with an incom-

ing edge unless that node is in a strongly connected

component (SCC). The algorithm identiﬁes nodes that

have only outgoing edges or are in a strongly con-

nected component with no incoming edges from out-

side the component. Only those nodes can be roots of

maximal lossless joins. From each root, the reachable

subgraph is found by traversing directed edges and an

algorithm for calculating all spanning trees (Gabow

and Myers, 1978) of the reachable graph is used to

ﬁnd all maximal lossless joins for each subgraph. Re-

peating the process for every potential root produces

all join sets without constructing any duplicates. The

algorithm is in Figure 6.

As the number of spanning trees may be exponen-

tial (such as for a completely connected graph), the

performance of the algorithm in the worst-case is ex-

ponential. In practice, database schemas do not ex-

hibit the worst case and tend to have a reasonable

number of maximal join trees. EMO outperforms a

grow all ways approach both in time and number of

edges and nodes visited. The performance improve-

ment is because EMO does not duplicate effort and

grows only from valid roots.

The following proofs demonstrate the correctness

of the algorithm by showing that EMO generates all

maximal join trees and only valid maximal join trees.

AUTOJOIN: PROVIDING FREEDOM FROM SPECIFYING JOINS

EMO (JoinGraph dg, List maxObjs)

{

allSCC = strongly connected components of dg

rGraphs = ∅

for each scc in allSCC

if (size scc == 1 and node has no in-edges)

rGraphs = rGraphs ∪ ﬁndReachable(n);

else

for each node n in scc

if (n has no in-edges from outside scc)

rGraphs = rGraphs ∪ ﬁndReachable(n);

maxObjs = ∅

for each reachable graph g in rGraphs

maxObjs = maxObjs ∪ g.ﬁndSpanningTrees()

}

Figure 6: EMO Algorithm

Theorem 1 EMO produces all maximal join trees.

Proof: Proof by contradiction. Let A be a maximal

join tree that is not produced by EMO. Let r be the

root of A. Let C be the strongly connected component

containing r.

Case 1: If C contains only one element, then r must

have no incoming edges. Otherwise, suppose it has

incoming edge (x, r). Adding (x, r) to A will pro-

duce a bigger tree containing A. That contradicts the

fact that A is a maximal join tree. So EMO will ﬁnd

the reachable graph of r.

Case 2: If C contains more than one element, then

EMO ﬁnds the reachable graph of every node in C

with no incoming edges from outside C. If r has no

incoming edges from outside C, EMO will ﬁnd the

reachable graph of r. If r has incoming edges from

outside C, then similar to Case 1, A is not a maximal

join tree.

In either case, A is one of the spanning trees of the

reachable graph of r. Thus, A is produced by EMO.

Theorem 2 Any spanning tree produced by EMO is

a unique maximal join tree.

Proof: Proof by contradiction. Suppose A is a tree

produced by EMO, but A is not a maximal join tree.

Then A must be a subtree of some maximal join tree

B. By Theorem 1, EMO produces B.

Case 1: Suppose A and B have the same root r.

Then A and B are both spanning trees of the reach-

able graph of r. This contradicts the fact that A is a

smaller tree contained in B.

Case 2: Suppose the root rA of A is contained in

B but is not the root of B. Then rA must have an

incoming edge e = (x, rA) where x is not contained

in A. EMO would not have found the reachable graph

for rA if it had an incoming edge unless rA was in a

strongly connected component C. Edge e may be an

incoming edge from outside C or an edge within C.

If it is an edge in C, x must be in A since x would be

reachable from rA. A contradiction as x is not in A. If

e is an incoming edge from outside C, then EMO will

not produce a spanning tree of the reachable graph

from rA. Thus, A would never be produced.

5 QUERY-TIME PROCESSING

It is critical to efﬁciently translate a user query into

one or more query interpretations for the relational

database. This computation will occur for every

query, where as the determination of maximal join

trees is performed only once. The strategy involves

quickly identifying and ranking all unique lossless in-

terpretations of the user query, then if necessary gen-

erating the join possibilities with a lossy join. The al-

gorithm for generating query interpretations executes

the following steps:

• Identify the maximal join trees that contain all the

user speciﬁed nodes (and edges).

• Prune identiﬁed trees to unique query interpreta-

tions, such that all leaf nodes are speciﬁed nodes.

• If required, generate all join graphs with a single

lossy join.

• Rank interpretations by the speciﬁed cost function

or default to minimal number of edges (joins).

To minimize processing time, several performance

improvements are implemented. First, AutoJoin pre-

computes a reverse index where each relation (node)

links to all the join trees containing this node. The in-

tersection of the sets of join trees results in all of the

unique join trees for the speciﬁed nodes. Second, in-

stead of recursively pruning leaf nodes of the maximal

join tree, a minimal join tree is built by performing a

union of the paths from the least common ancestor

of all requested nodes to each requested node. The

ancestor lists are precomputed with the maximal join

trees prior to query time.

5.1 Extension to Lossy Joins

For queries that do not have a lossless interpretation

or require additional interpretations, query interpreta-

tions involving a lossy join are generated. These addi-

tional interpretations are created by the union of pairs

of maximal join trees that together contain all the re-

quested nodes and have at least one node in common.

The union of these join trees will contain one or more

nodes with more than one incoming edge. A prune

method generates all minimal interpretations with a

single lossy join. The AutoJoin inference engine gen-

erates query interpretations as a connected graph con-

ICEIS 2005 - HUMAN-COMPUTER INTERACTION

taining all of the speciﬁed nodes with a single node

having two incoming edges.

5.2 Beyond Natural Joins

The main focus of this work is on natural joins of for-

eign keys as they are the most common type of join.

However, query inference is not restricted to queries

with only natural joins. In general, any complex join

condition can be speciﬁed and the query inference en-

gine will infer any natural joins still required to com-

plete the query. A theta join is handled by merging

the two join nodes in the original join graph and up-

dating the edges. Due to EMO’s efﬁciency, it is pos-

sible to compute the maximal join trees for the mod-

iﬁed join graph and apply the regular query inference

algorithm. Maier and Ullman provide a method for

inferring queries involving tuple variables (Maier and

Ullman, 1983). Tuple variables allow one or more

relations to occur in a query multiple times, allowing

for query inference of more complicated queries. Any

query interface built on the AutoJoin inference engine

may allow the user to specify such complex queries

by specifying additional nodes and edges required to

be in the query interpretations. Query inference can

be applied to any query including ones that use sub-

queries, complex join predicates and outer joins.

6 PERFORMANCE

EXPERIMENTS

The AutoJoin inference engine is implemented in Java

and uses the JDBC API to extract schema informa-

tion. All schemas are in production use at various or-

ganizations or extracted from the Internet. The largest

schema is caBIO from the NCI Cancer Grid project

(caBIG)

which contains 149 nodes, 213 edges, and

1253 maximal join trees. The experiments were per-

formed on a 1.3 GHz AMD Athlon with 512 MB of

memory running Windows XP.

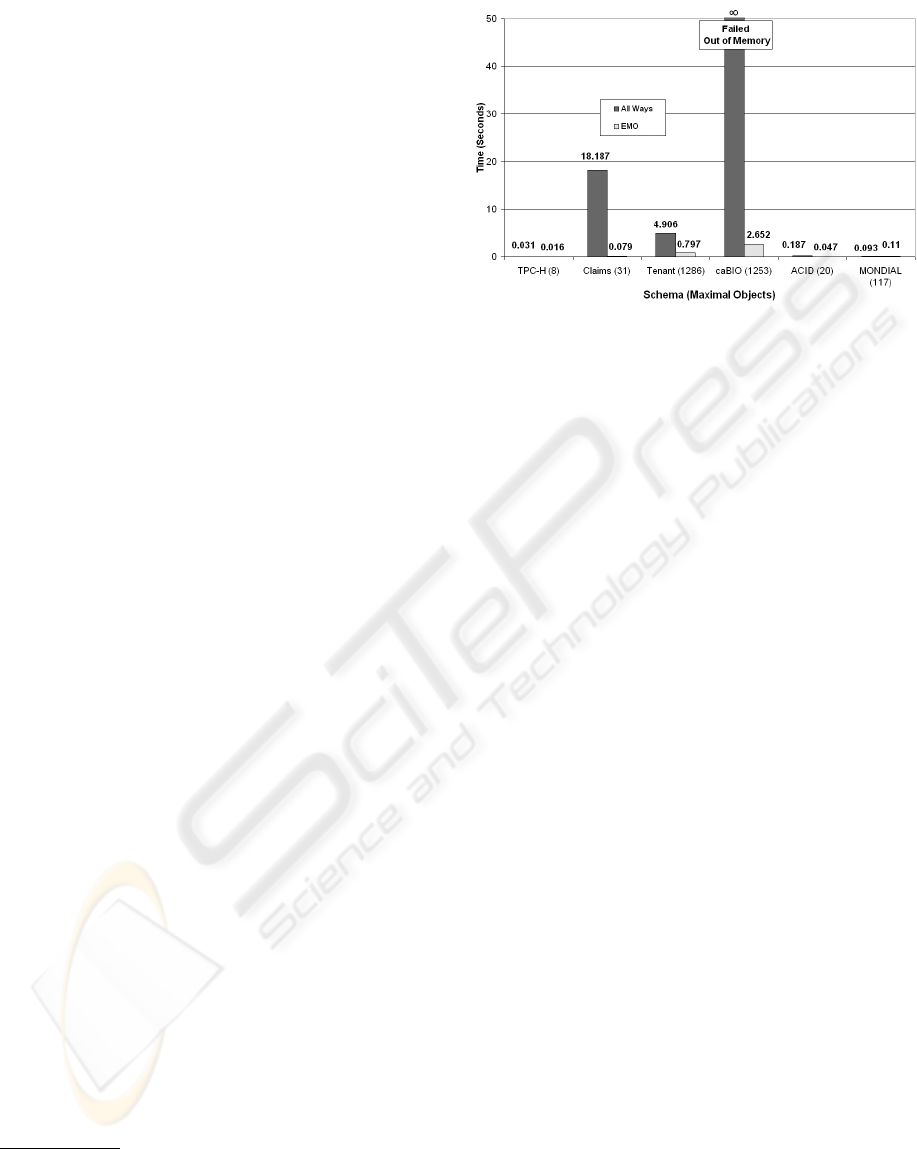
The ﬁrst experiment compares the performance of

EMO with the grow all ways approach used in (Maier

and Ullman, 1983; Semmel and Mayﬁeld, 1997; Hris-

tidis and Papakonstantinou, 2002). The results in Fig-

ure 7 show that EMO signiﬁcantly outperforms the

grow all ways approach. The grow all ways approach

is very inefﬁcient and cannot complete the caBIO

schema without running out of memory.

Both ap-

proaches are comparable for very small graphs. EMO

http://cabig.nci.nih.gov/

The grow all ways algorithm is either CPU or mem-

ory constrained depending on breadth ﬁrst or depth ﬁrst

growth. The DFS approach did not complete for the Claims

or CaBIO database.

Figure 7: Time to Compute Maximal Join Trees

outperforms on large graphs by an order of magni-

tude, which is especially important when schema evo-

lution is frequent. EMO is able to handle schemas

that could not even be processed by the existing ap-

proaches. EMO’s absolute performance is sufﬁciently

fast to support generation of maximal join trees at

query-time for almost all database schemas.

The second experiment determines how removing

shortcut joins reduces ambiguity. We use the TPC-H

schema and determine the percentage of queries that

are unambiguous before and after removing short-

cut joins. All 255 potential queries were treated as

equally likely (all queries of one table, of two tables,

etc.). Removing shortcut joins improved the number

of unambiguous queries from 8% to 26% (see Figure

8). Of the 22 benchmark TPC-H queries, removing

shortcut joins made 68% of the queries unambiguous

versus 45% originally. Several benchmark queries

contain nested subqueries. We consider a query to

be unambiguous if both the join tree for the subquery

and outer query is unambiguous. Query 5 contains

a lossy join, and two queries (7 and 8) require two

copies of Nation that must be speciﬁed by the user.

The hierarchical EDS schema shows an even greater

improvement by removing shortcut joins.

The overhead of performing query inference for

each query must be minimal. In a third experiment,

we determine the time to perform query inference on

various schemas. We calculated the average time to

infer the joins for the 22 benchmark TPC-H queries,

for all possible 255 TPC-H queries, and for two table

lossless queries in the other sample databases. As Fig-

ure 9 shows, the average query inference time is well

below 10 ms even for large schemas. Removing short-

cut joins improves the time for TPC-H. The inference

time for caBIO only slightly increases despite the sig-

niﬁcantly larger schema size. By building query in-

terpretations using least common ancestor versus re-

AUTOJOIN: PROVIDING FREEDOM FROM SPECIFYING JOINS

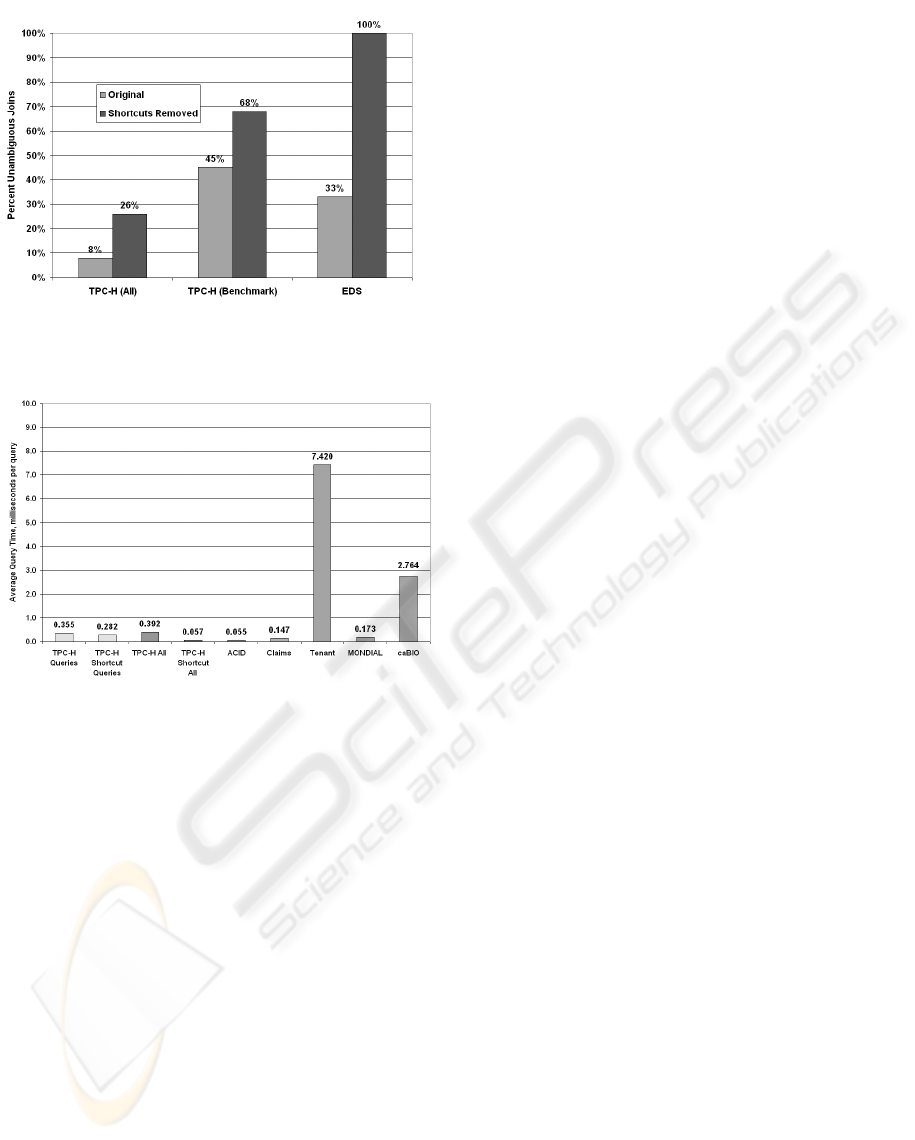
Figure 8: Reducing Ambiguity by Removing Shortcut Joins

Figure 9: Query Inference Time

cursive pruning, the average inference time decreased

from 126 ms to 2.7 ms on caBIO. The lossy join in

TPC-H query 5 is speciﬁed for this experiment. If it

was not speciﬁed, the time to compute all lossless and

one-lossy interpretations (using the strategy in Sec-

tion 5.2) was 16 ms (after removing shortcut joins).

Thus, the time to infer a query is minimal.

7 CONCLUSION

By combining the algorithms to address the chal-

lenges of query inference into a single inference en-

gine, AutoJoin provides a comprehensive tool for de-

veloping the next generation of query interfaces. In

addition, it provides a method to create SQL queries

without requiring full knowledge of the database.

Inference is possible on larger and more complex

schemas, due to the efﬁcient maximal join tree algo-

rithm EMO. By precomputing these potential joins,

the majority of computation occurs only once, prior

to query time. Identiﬁcation and removal of semanti-

cally equivalent shortcut joins reduces the number of

ambiguous queries further improving inference. Pre-

determined look up tables combined with indexing

of potential joins allows for efﬁcient identiﬁcation of

joins for each query. Numerous performance experi-

ments on diverse schemas demonstrate that the time

to infer these joins for each query is minimal. In

addition, the complexity of queries inferred exceeds

any previous individual inference method. AutoJoin

is a general inference engine conﬁgurable to speciﬁc

query interface requirements. This allows for the con-

tinued development of simpler keyword, conceptual,

and natural language query interfaces without the bur-

den of developing a scalable and efﬁcient join de-

termination algorithm. Overall, query inference is

a practical query tool to incorporate into query lan-

guages and database systems.

REFERENCES

Agrawal, S., Chaudhuri, S., and Das, G. (2002). DBX-

plorer:A System for Keyword-Based Search Over Re-

lational Databases. In IEEE ICDE, pages 5–16.

Balmin, A., Hristidis, V., and Papakonstantinou, Y. (2004).

ObjectRank:Authority-Based Keyword Search in

Databases. In VLDB, pages 564–575.

Catarci, T. (2000). What happend when Database

Researchers met Usability. Information Systems,

25(3):177–212.

Gabow, H. and Myers, E. (1978). Finding All Spanning

Trees of Directed and Undirected Graphs. SIAM Jour-

nal of Computing, 7(3):280–287.

Hristidis, V. and Papakonstantinou, Y. (2002). DIS-

COVER:Keyword Search in Relational Datbases. In

VLDB, pages 670–681.

Maier, D. and Ullman, J. (1983). Maximal Objects and the

Semantics of Universal Relation Databases. TODS,

8(1):1–14.

Owei, V. and Navathe, S. (2001). Enriching the con-

ceptual basis for query formulation through relation-

ship semantics in databases. Information Systems,

26(6):445–475.

Popescu, A., Etzioni, O., and Kautz, H. (2003). Towards a

theory of natural language interfaces to databases. In

IUI.

Semmel, R. and Mayﬁeld, J. (1997). Automated Query

Formulation using an Entity-Relationship Conceptual

Schema. Intelligent Information Systems, 8:267–290.

Wald, J. and Sorenson, P. (1984). Resolving the Query

Inference Problem Using Steiner Trees. TODS,

9(3):348–368.

Zhang, G., Meng, F., Kong, G., and Chu, W. (1999). Query

Formulation from High-level Concepts for Databases.

In User Interfaces to Data Intensive Systems.

ICEIS 2005 - HUMAN-COMPUTER INTERACTION