
THE HYBRID DIGITAL TREE: A NEW INDEXING TECHNIQUE
FOR LARGE STRING DATABASES
Qiang Xue and Sakti Pramanik
Department of Computer Science and Engineering
Michigan State University, East Lansing, MI 48824, USA
Gang Qian
Department of Computer Science
University of Central Oklahoma, Edmond, OK 73034, USA
Qiang Zhu
Department of Computer and Information Science
The University of Michigan,Dearborn, MI 48128, USA
Keywords:
Hybrid Digital tree, indexing, string databases, prefix searches, substring searches.
Abstract:
There is an increasing demand for efficient indexing techniques to support queries on large string databases.
In this paper, a hybrid RAM/disk-based index structure, called the Hybrid Digital tree (HD-tree), is proposed.
The HD-tree keeps internal nodes in the RAM to minimize the number of disk I/Os, while maintaining leaf
nodes on the disk to maximize the capability of the tree for indexing large databases. Experimental results
using real data have shown that the HD-tree outperformed the Prefix B-tree for prefix and substring searches.
In particular, for distinctive random queries in the experiments, the average number of disk I/Os was reduced
by a factor of two to three, while the running time was reduced in an order of magnitude.
1 INTRODUCTION
Electronic text (string) collections have increased dra-
matically over the last decade, from megabytes of dic-
tionaries, to gigabytes of genome sequences, to ter-
abytes of web documents. Many applications need
efficient indexing methods to process complex string
queries (e.g., substring searches) on these large string
data sets. In the past few decades, various data struc-
tures have been proposed for string indexing. They
can be divided into two categories: RAM-based and
disk-based. The first category includes digital-tree-
based (trie-based) structures, such as the Patricia trie
(Morrison, 1968), the suffix tree (McCreight, 1976;
Weiner, 1973), the suffix array (Manber and My-
ers, 1990), and the PAT tree (Gonnet et al., 1991).
The second category includes the extendible hashing
(Fagin et al., 1979), inverted files (Baeza-Yates and
Ribiero-Neto, 1999), the Prefix B-tree (Bayer and Un-
terauer, 1977), and the String B-tree (Ferragina and
Grossi, 1999).
RAM-based index structures reside in the main
memory (RAM) where string queries are performed.
Among these RAM-based structures, Patricia tries
and PAT/suffix trees are particularly effective in han-
dling relatively small amount of string data; however,
as the database size increases, it is no longer feasi-
ble to keep the trie structure in the RAM. Moreover,
because of the unbalanced structure of tries, it is inef-
ficient to store tries on disk, especially when indexes
are dynamically created (Clark and Munro, 1996; Fer-
ragina and Grossi, 1999). Therefore, we argue that
RAM-based index structures are not suitable for in-
dexing large string databases.
On the other hand, disk-based data structures can
be used for indexing large string databases. Among
these disk-based structures, hashing technology is ef-
ficient for exact string matches and inverted files are
efficient for keyword-based searches; however, they
are unsuitable for substring searches. The Prefix B-
tree is capable of indexing large and dynamic string
databases. The String B-tree (Ferragina and Grossi,
1999) uses the Patricia trie inside its internal nodes
to provide the same worst-case performance as the B-
tree (Bayer and McCreight, 1972). Since the String
B-tree stores indexed strings in a separate file, it re-
quires more disk accesses than the Prefix B-tree in
general case. These disk-based indexing techniques
115
Xue Q., Pramanik S., Qian G. and Zhu Q. (2005).
THE HYBRID DIGITAL TREE: A NEW INDEXING TECHNIQUE FOR LARGE STRING DATABASES.
In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 115-121
DOI: 10.5220/0002518501150121
Copyright
c
SciTePress
require limited RAM to conduct string queries. To
utilize the large amount of available memory, they
rely on caching mechanisms that are usually not opti-
mized for individual data structure.
In this paper, we propose the Hybrid Digital tree
(HD-tree), a novel hybrid RAM/disk-based index
structure to support efficient queries on very large
string databases. The HD-tree keeps its internal
nodes, which are similar to those in digital trees, in
the RAM to minimize the number of disk I/Os for a
string query. Its leaf nodes, which hold the suffixes of
the indexed strings, are kept on disk to maximize the
capability of the tree for indexing a large database.
It is known that traditional disk-based trees, such as
Prefix B-trees, may use the available RAM to keep
their internal nodes (i.e., caching), so that the num-
ber of disk I/Os may be reduced. However, the HD-
tree is different from this approach as follows: First,
an internal node of disk-based trees is a disk block,
which is usually several kilobytes in size, while an in-
ternal node of the HD-tree is a data structure (i.e., a
trie node), which is usually several bytes in size. Sec-
ond, the internal nodes of disk-based trees are stored
on disks and have to be read into the RAM whenever
is necessary, while all internal nodes of the HD-tree
are kept in the RAM, so that no disk I/Os are required
to access these internal nodes.
The internal nodes of a HD-tree are built on the
prefixes of indexed strings and are used to guide the
search to the leaf node(s) containing the query an-
swer(s). Unlike a traditional digital tree, the parent
of a leaf node in the HD-tree allows a set (“range”) of
multiple prefixes so that indexed strings with different
prefixes may share the same leaf node (disk block) to
improve disk utilization. Moreover, unlike the tradi-
tional concept of range, the above prefix “range” of
a node may not be “continuous”, so that strings with
a prefix within the traditional range may be stored in
a separate leaf node(s) to allow further improvements
in disk utilization.
We did extensive experiments to study the behavior
of the HD-tree under different RAM sizes for various
string queries. It was observed that for a given data-
base size, a small amount of RAM improved the per-
formance of the HD-tree significantly; however, when
the RAM size was increased beyond a certain thresh-
old point, the gain in performance became less sig-
nificant. We also conducted experiments to evaluate
the performance of the HD-tree by comparing to the
Prefix B-tree. The experimental results showed that
the HD-tree outperformed the Prefix B-tree given the
same amount of RAM.
The rest of this paper is organized as follows: the
structure and algorithms of the HD-tree are described
in Section 2; experimental results using Text RE-
trieval Conference (TREC) collections (Voorhees and
Harman, 1997) are discussed in Section 3; conclu-
sions and future work are presented in Section 4.
2 THE HD-TREE
The HD-tree incorporates and extends some indexing
strategies of the digital tree and the B
+
-tree (Comer,
1979), taking advantages of their strengths in search
performance, compression capability, and disk uti-
lization. We first introduce the notation and assump-
tions used in this paper. A string consists of a se-
ries of letters (symbols) chosen from an alphabet Σ of
size |Σ|. The letters and strings are assumed to have a
lexicographic order. Symbols from Σ are denoted by
lower-case letters (e.g., a, b, and c), while strings are
denoted by lower-case Greek letters (e.g., α, β, and
γ). ♯ is a special auxiliary symbol such that ♯ /∈ Σ
and ♯ < c for any c ∈ Σ. Given a string α=a
1
...a
n
of
length |α|=n, we call a
1
...a
i
a prefix, a
j
...a
n
a suffix,
and a
i
...a
j
a substring of α, where 1 ≤ i ≤ j ≤ n.
Given a set Ω of letters, function MAX(Ω) yields the
greatest element in Ω. The database is considered as a
set of records with the form Υ
i
=(κ
i
, Λ
i
), where κ
i
is
a unique string and Λ
i
is the descriptive information
of κ
i
, such as statistic, offset, or a pointer to another
location where the information can be found. Since
the focus of this paper is on studying the issues of
string indexing, Λ
i
is ignored in our discussion (i.e.,
not strictly distinguishing a record and a string). Fi-
nally, databases are assumed to be too large to utilize
a RAM-based index technique.
2.1 HD-tree Structure
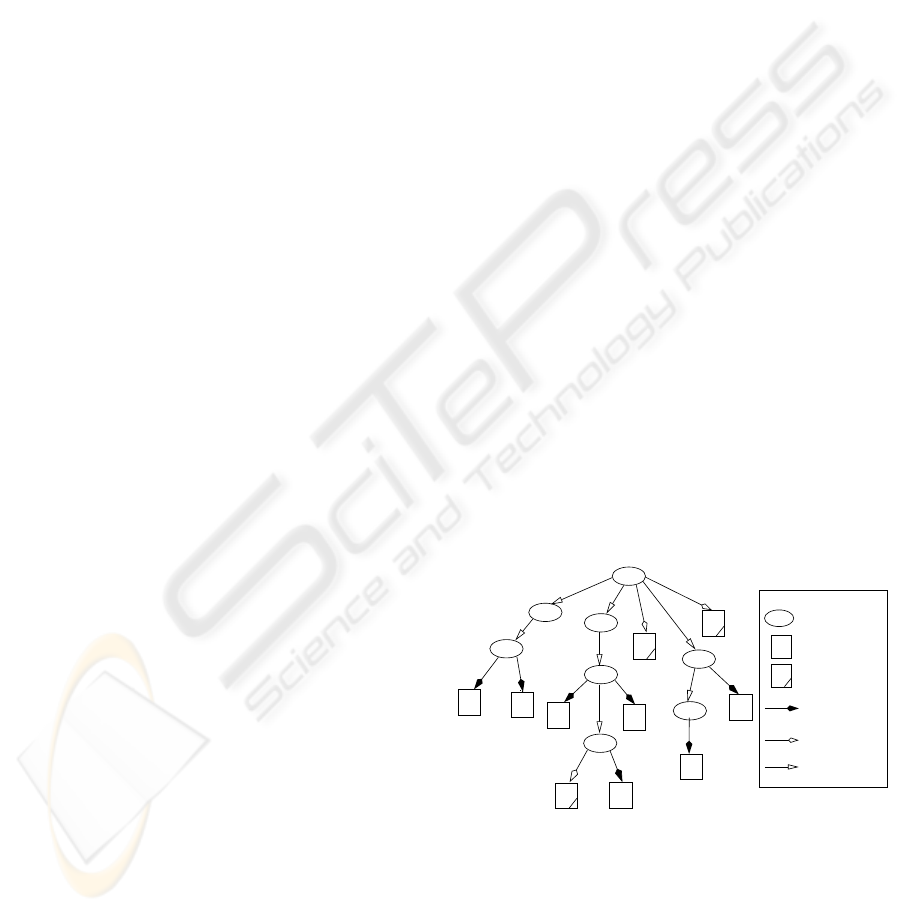
Multi−Group
Leaf node
Single−Group
Leaf node
Multi−Group
Leaf Pointer
Single−Group
Leaf Pointer
Internal
Pointer
8
14
a
b
e
9
5
a
b
e
b
b
e
c
c
d
b
e
c
d
3
15
17
18
13
11
10
7
6
1
2
d
16
4
12
Alphabet:
{a, b, c, d, e}
Internal Node
Figure 1: An HD-tree
The HD-tree is an unbalanced and ordered tree. An
internal node δ of the HD-tree contains a list of pairs
L(δ)={(a
1
, P
1
), ..., (a
m
, P
m
)}, where P
i
is a pointer
to its child node; a
i
(1 ≤ i ≤ m) is a letter from
Σ, called the label of P
i
; and a
1
< ... < a
m
, such
that the pointers are ordered according to their labels.
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
116

Leaf nodes, which are implemented as disk blocks,
contain the suffixes of indexed strings. The id-string
of a tree node is the concatenation of the labels along
the path traversing from the root to the node. The
id-string of the root is empty. Note that an HD-tree
node can be uniquely identified by its id-string. Let
ID(δ) denote the id-string of a tree node δ. In Figure
1, ID(2)=a, ID(9)=bbe, and ID(15)=db. An HD-
tree must satisfy two basic properties that determine
the proper leaf node for the indexed strings.
PROPERTY
1 For each internal node δ in an HD-tree,
ID(δ) is a common prefix of all strings contained in
any leaf node in the sub-tree with δ as the root.
Property 1 is similar to that of a digital tree; however,
the id-string of a leaf node δ
′
in an HD-tree repre-
sents one or more prefixes (prefix-set) that strings in
δ
′
may have. Let P S(δ
′
) be the prefix-set of δ
′
. If
|P S(δ
′
)|=1, all strings in δ
′
share the same prefix in
P S(δ
′
). We call such a leaf node a Single-Group Leaf
(SGL). If |P S(δ
′
)| > 1, leaf node δ
′
contains sev-
eral groups of strings, where the strings in each group
share a prefix that is different from the prefix of an-
other group. We call such a leaf node a Multi-Group
Leaf (MGL). The reason for using SGL and MGL is
to improve the disk utilization. Otherwise, some large
groups of strings may hinder the grouping of small
groups. Note that, based on Property 1, all prefixes
in PS(δ
′
) are different only at their last letters. An
internal node in an HD-tree may have three types of
pointers: (1) Internal Pointer (IP) to an internal node,
(2) Single-Group Leaf Pointer (SGLP) to an SGL, and
(3) Multi-Group Leaf Pointer (MGLP) to an MGL.
A key range in a traditional index tree, such as the
B-tree, is continuous, where no key between the two
boundaries of the range can be excluded; however, the
prefix-set (i.e., the prefix “range”) in the HD-tree may
not be continuous because one or more prefixes be-
tween the two boundaries (minimum and maximum
prefixes) of the range may be excluded. The prefix-
set P S(δ
′
) for an SGL δ
′
contains the unique pre-
fix ID(δ
′
), i.e., P S(δ
′
)={ID(δ
′
)}. For example, in
Figure 1, node 11 is an SGL where P S(11)={bbcc};
that is, all strings in this node have the common pre-
fix bbcc. It is the task of the tree-building algorithm to
determine which node is an SGL.
Unlike an SGL, where its prefix-set is directly pre-
sented by its id-string, the prefix-set of an MGL
needs to be derived as follows. Let δ
′
be an
MGL, and δ be the parent node of δ
′
containing
the list L(δ)={(a
1
, P
1
, ... , (a
k
, P
k
), ... , (a
m
, P
m
)},
where m > 0 and P
k
is the pointer to δ
′
. Let
β=ID(δ). The prefix-set of the MGL δ
′
is defined
as: P S(δ
′
)={βc | c ∈ Ω
P
k
}, where Ω
P
k
is a set of
letters obtained through the following steps:
1) Ω
′
P
k
={a
i
| (a
i
, P
i
) ∈ L(δ), a
i
< a
k
,
P
i
is an MGLP};
2) if (Ω
′
P
k
is empty ) b
′
=♯; else b
′
= MAX( Ω
′
P
k
);
3) Ω
Σ
={a | a ∈ Σ, b
′
< a≤ a
k
};
4) Ω
′′
P
k
={a
j
| (a
j
, P
j
) ∈ L(δ), b
′
< a
j
< a
k
,
P
j
is an IP or SGLP};
5) Ω
P
k
=Ω
Σ
−Ω
′′
P
k
.
For example, in Figure 1, P S(9)={bbd,bbe} and
P S(12)={bbca, bbcb, bbcd}.
PROPERTY
2 Each leaf node δ
′
in an HD-tree keeps
all the indexed strings with a prefix in its prefix-set
P S(δ
′
).
Based on the previous discussion on the prefix-set,
Property 2 of the HD-tree guarantees that any string
is placed in one and only one leaf node of an HD-tree.
Although we may logically consider that each string
is kept in a leaf node, the entire string does not have to
be stored in the leaf node physically, since the prefix
of a string can be found along the path from the root
to a leaf node. Therefore, only the suffix of a string is
stored in a leaf node.
2.2 Building the HD-Tree
To build an HD-tree, algorithms are needed for inser-
tion, deletion, and update. Due to the limitation of
space, only the insertion and its related issues are de-
scribed in this paper. Interested readers can refer to
(Xue et al., 2004) for detail algorithms.
2.2.1 Insertion Procedure
The insertion procedure is to insert a new string κ
into a given HD-tree where κ=k
1
...k
n
, k
i
∈ Σ, and
1 ≤ i ≤ n. Note that ♯ is appended at the end of a
string to distinguish the string from any id-string in
the given HD-tree. Assume the root of an HD-tree
is at level 1. Given an internal node δ at level l, k
l
is used to determine the next pointer to follow. The
insertion procedure first follows internal pointers (k
l
must equal to the label) down the tree as far as possi-
ble. It stops at an internal node δ which satisfies the
following: P S(δ)=k
1
...k
i
; and for any internal node
δ
j
in the tree, if P S(δ
j
)=k
1
...k
j
then j ≤ i. The letter
k
i+1
is then used to find a qualified leaf node (a child
of δ) according to Property 2. If no leaf node is qual-
ified, either the right-most MGL is chosen (if avail-
able) and its prefix-set is expanded, or a new MGL is
created. Finally, the suffix string k
i+1
...k
n
is stored
in the selected leaf node δ
′
. If δ
′
overflows after the
insertion, the overflow processing is invoked. For ex-
ample, in Figure 1, to insert a string bbab, δ is the
internal node 7, δ
′
is the leaf node 8, and ab is stored
in node 8. In the same way, string bbcca is stored in
node 11 as ca, string bbcab is stored in node 12 as ab.
THE HYBRID DIGITAL TREE: a new indexing technique for large string databases
117

2.2.2 Overflow Processing
In HD-trees, only suffixes of the original strings are
stored in a leaf node. These suffixes are called suffix-
strings. A suffix-group is a set of suffix-strings whose
first letters are the same (see Figure 2). If the over-
flow leaf node δ
′
(whose parent is δ
1
) is an SGL, a
new internal node δ
2
is created, the first letter of each
suffix-string in δ
′
is removed; δ
2
becomes the child of
δ
1
; δ
′
becomes the child of δ
2
(i.e., the grandchild of
δ
1
). Consequently, the tree grows to another level. If
the overflow leaf node δ
′
is an MGL, it is considered
for splitting.
caa cb cbce
dca dcc
eab edea eee
A Multi−Group Leaf
node 17
cbba cbcd
caa cbc cdd ce
cabd cac
A Single−Group Leaf
node 11
group
a
Figure 2: The SGL and the MGL
2.2.3 Splitting
When an MGL is split, the suffix-strings in δ
′
must
be moved by one suffix-group at a time. If the MGL
δ
′
is split into two whenever it overflows (SSplit), the
disk utilization is shown to be very low. In order to
improve the disk utilization, two heuristics are used
(HD-Split): (1) if the size of a suffix-group is greater
than a threshold T (we use 85% of the disk block size
in our experiments), an SGL containing this suffix-
group is formed; (2) before an overflow node is split
or after an SGL is moved out of an overflow leaf node,
suffix-groups may be moved to the qualified left or
right siblings to avoid creating a new leaf node.
2.2.4 Linked Disk Blocks
The HD-tree keeps track of the current available
RAM whenever adding or deleting an internal node.
If the RAM is available, the tree grows by creating
internal nodes through the overflow processing. Oth-
erwise, the tree stops creating new internal nodes.
Hence, if a leaf node overflows after inserting a string,
an extra disk block is linked to the original disk block
to accommodate the overflowing data. Consequently,
a search within the leaf node needs to access all linked
disk blocks. Using this approach, the HD-tree works
with any given size of RAM.
2.2.5 Queries
After an HD-tree is created, various queries can be ef-
ficiently processed using the tree. Given a database
containing strings κ
1
, ..., κ
n
, an ExactSearch(α)
retrieves κ
i
such that κ
i
=α, 1 ≤ i ≤ n; a
P ref ixSearch(α) retrieve κ
i
where α is a prefix
of κ
i
; a SubstringSearch(α) retrieves κ
i
where
α is a substring of κ
i
. Note that in the HD-
tree, ExactSearch(α) equals to P ref ixSearch(α♯)
and SubstringSearch(α) is processed by perform-
ing P refixSearch(α) among all suffix strings of
κ
1
, ..., κ
n
(Ferragina and Grossi, 1999).
3 EXPERIMENTAL RESULTS
We conducted extensive experiments to analyze the
behavior of the HD-tree and evaluate its performance.
The string databases were generated from TREC
(Voorhees and Harman, 1997). The HD-tree was im-
plemented using C++. Experiments were conducted
on a PC running Linux OS. The disk block size used
in our experiments was 4096 bytes.
Sample database WSJ1 was generated from the
TREC collection, Wall Street Journal 1991, by first
removing tags and breaking the text into segments of
5MB each, then extracting unique prefixes of the suf-
fix strings at non-space letters for every segment, and
keeping the first 32 letters if the prefix string is longer
than 32. WSJ1 can be used for keyword-based docu-
ment searches (Baeza-Yates and Ribiero-Neto, 1999)
or substring searches (Gonnet et al., 1991) depending
on the starting boundaries (either words or letters) of
the suffix strings. WSJ1 contained 15 million strings
and each string was associated with a four-byte inte-
ger as the descriptive information. The size of WSJ1
was 252MB.
Table 1: Split heuristics on disk utilization
DBSize(M B) 50 100 150 200 250
SSplit 45.7 44.8 44.6 44.5 44.1
HD-Split 65.1 63.5 63.1 62.7 62.6
Improvement 42.5 41.7 41.5 40.1 42.0
Databases: Samples from WSJ1, Table value: %
3.1 Split Heuristics
One set of experiments is to show the effectiveness
of the split heuristics for building an HD-tree. Table
1 shows the comparison of the disk utilization (using
one disk block for each leaf node) between the SSplit,
which is a B
+
tree-like approach, and the HD-Split
(see Section 2.2.3). Note that the HD-Split adopted
two heuristics to improve the disk utilization. One is
to distinguish the SGL from the MGL, which allows
the prefix range to be “non-continuous”. The other is
to move groups to left or right sibling to avoid a split,
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
118
which dynamically adjusts the prefix-set of an MGL.
It is shown that the HD-Split increases the disk uti-
lization by more than 40%, which indicates the effec-
tiveness of the grouping mechanism in the HD-Split.
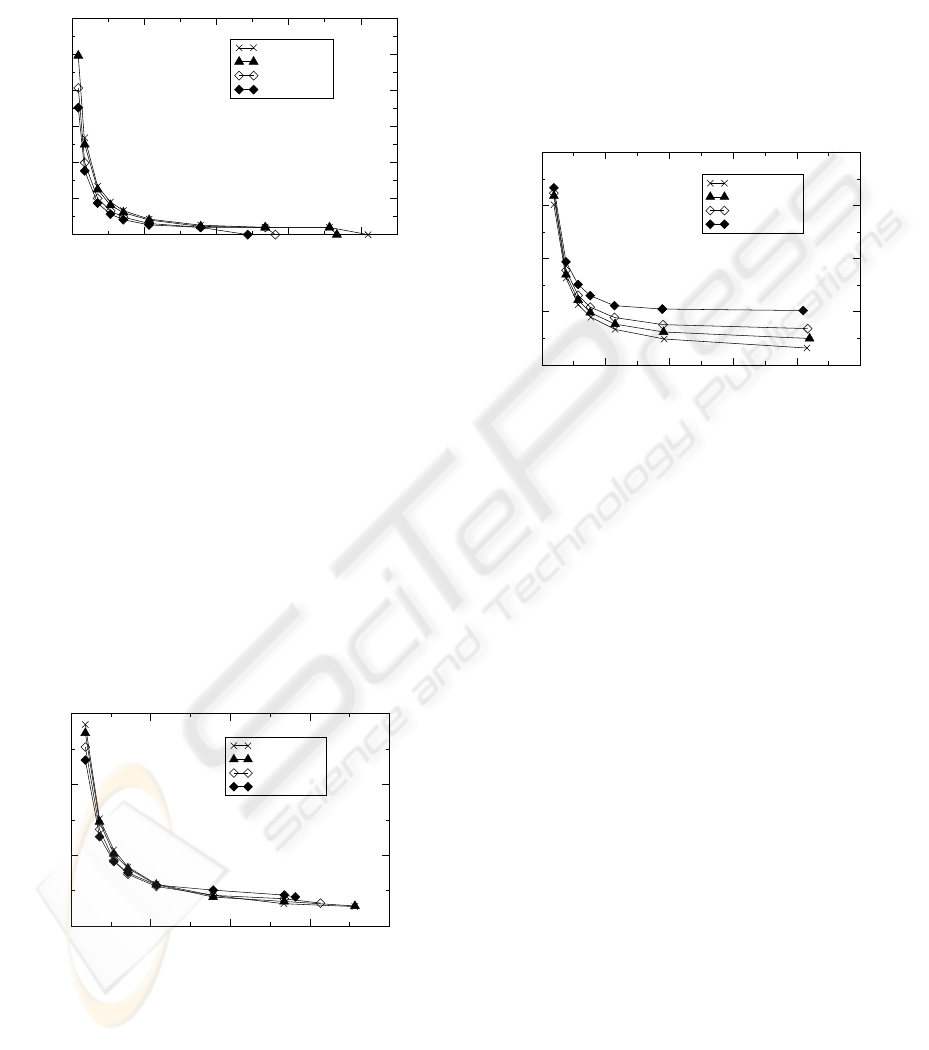
0 0.1 0.2 0.3 0.4
RAM Size as the Percentage of the Database Size
0
5
10
15
20
25
30
Average Number of Links
DB 25MB
DB 50MB
DB 150MB
DB 250MB
DBs: Samples from WSJ1
Figure 3: The relationship between the ANL and the avail-
able RAM as the percentage of the database size.
3.2 Query Performance
As described in Section 2.2.4, using linked disk
blocks, the HD-tree is scalable for any RAM size.
Figure 3 shows the relationship between the average
number of links (ANL) and the available RAM size
as the percentage of the database size (RAM/DB).
The ANL is the total number of linked disk blocks
divided by the number of linked leaf nodes. An ANL
value of zero means that each leaf node occupies one
disk block. It is shown that the ANL decreases as the
RAM/DB increases. Note that there exists a thresh-
old (where the curve becomes flat) in the figure. The
threshold is almost invariant of database sizes.
0 0.1 0.2 0.3 0.4
RAM Size as the Percentage of the Database Size
0
5
10
15
Number of Disk I/Os per Query
DB 25MB
DB 50MB
DB 150MB
DB 250MB
DBs: Samples from WSJ1
Figure 4: The relationship between the number of I/Os and
the available RAM when the answer size is fixed.
When ANL is greater than zero (i.e., the linked disk
blocks are used), the query performance of the HD-
tree is shown to be closely related to the ANL. Curves
in Figures 4 and 5, where the number of I/Os rather
than ANL is used, are similar to those in Figure 3. The
phenomenon of a threshold can be explained by the
following: because of the logarithmic nature of the
tree (i.e., lower level contains less nodes), as the HD-
tree grows, adding the same amount of the RAM (i.e.,
adding certain number of leaf nodes) has less impact
on the selectivity of the tree (i.e., the total number of
leaf nodes). Therefore, when the available RAM is
limited compared to the databases size, it is important
to allocate enough RAM at the threshold point where
the RAM is most effectively utilized.
0 0.1 0.2 0.3 0.4
0.5
RAM Size as the Percentage of the Database Size
0
5
10
15
20
Number of Disk I/Os per Query
DB 50MB
DB 100MB
DB 150MB
DB 250MB
DBs: Samples from WSJ1
Figure 5: The relationship between the number of I/Os and
the available RAM when the answer size changes.
3.3 Comparisons
In this subsection, we evaluate the performance of the
HD-tree by comparing it with that of the Prefix B-
tree. The Prefix B-tree is widely adopted by data-
base systems and has been shown to be a practical
technique for indexing large string databases. The
Prefix B-tree we used was implemented by the popu-
lar Berkeley DB (Sleepycat, 2004), which is an open
source database system. As a disk-based index struc-
ture, the Prefix B-tree does not use any memory, while
the HD-tree requires certain amount of RAM to keep
its internal nodes. For a fair comparison, we pro-
vided the same amount of RAM used by the HD-tree
for the Prefix B-tree as a cache. The caching algo-
rithm is based on the popular LRU (least-recently-
used) heuristic, which is used by almost all commer-
cial database systems because of its simplicity and ef-
fectiveness. The LRU algorithm keeps recently ac-
cessed internal nodes in the RAM to reduce the num-
ber of disk I/Os.
We first compared the disk I/Os between the HD-
tree and the Prefix B-tree using 1000 queries with dif-
ferent numbers of distinctive queries. This set of ex-
periments was designed to evaluate the effect of the
locality of the query results on the performance of the
HD-tree and the Prefix B-tree. The queries are gen-
erated as follows: (1) select a certain number of dis-
tinctive queries to form a query pool; (2) randomly
THE HYBRID DIGITAL TREE: a new indexing technique for large string databases
119
generate 1000 queries from the query pool. In one
extreme case, the 1000 queries are all the same. As
the number of distinctive queries increases, the level
of localities in the query results reduces. The other
extreme is when all 1000 queries are different.
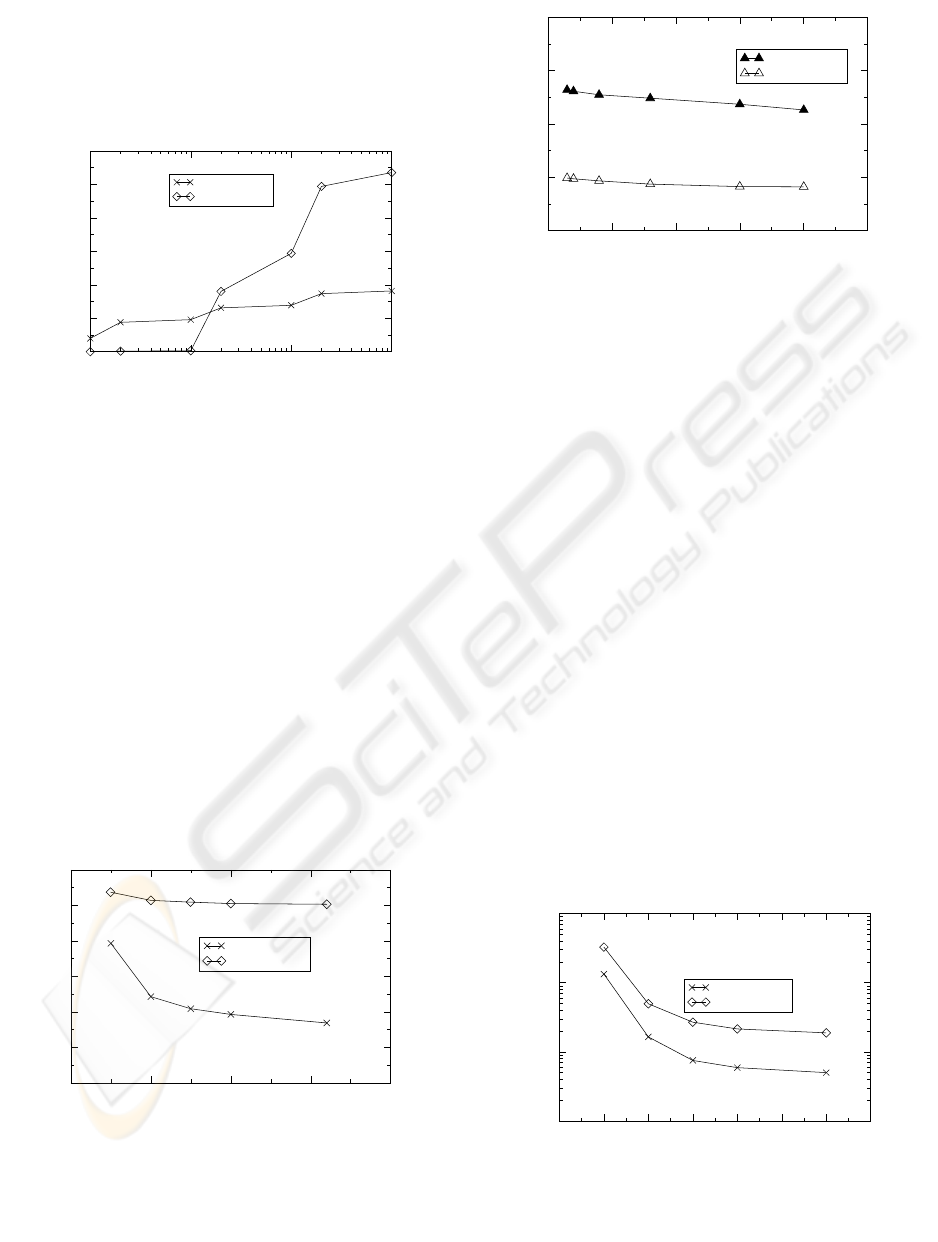
1 10 100 1000
Number of Distinctive Queries
2500
5000
7500
10000
12500
15000
Total Number of Disk I/Os
HD-tree
Prefix B-tree
Figure 6: I/O comparison for different query localities; av-
erage query length is 6.
As shown in Figure 6, the performance of the Pre-
fix B-tree is better when the number of distinctive
queries is small. However, as the number of distinc-
tive queries increases, the performance of the Pre-
fix B-tree deteriorates quickly. The two curves cross
between 10 and 20 distinct queries, where the HD-
tree starts to outperform the Prefix B-tree. For 1000
distinctive queries, the HD-tree is almost three times
better than the Prefix B-tree in term of the number
of disk I/Os. The results show that the performance
of the Prefix B-tree using the LRU caching mecha-
nism is very susceptible to the locality of the query
results. On the other hand, the HD-tree is quite robust
to different queries. We conclude that the HD-tree
performs better as queries become more different. In
the following I/O comparisons, we used 1000 random
distinctive queries.
0
500
1000
1500
2000
RAM Size (KB)
0
1
2
3
4
5
6
Number of Disk I/Os per Query
HD-tree
Prefix B-tree
Figure 7: I/O comparison for different RAM sizes; average
query string length is 8.
In Figures 7 and 8, we compare the performance of
the HD-tree and the Prefix B-tree for different RAM
sizes. In Figure 7, it is shown that the HD-tree not
0
5
10
15
20
25
RAM Size (Mb)
0
5
10
15
20
Number of Disk I/Os per Query
HD-tree
Prefix B-tree
Figure 8: I/O comparison for different RAM sizes; average
query string length is 6.
only reduces the number of I/Os, but also uses the
RAM more effectively than the caching mechanism
adopted by the Prefix B-tree. For example, as the
RAM increases from 250KB to 1.6MB, the HD-tree
reduces more than 50% of I/Os, but the Prefix B-tree
only reduces less than 20% of I/Os. For the given
database WSJ1 (252MB) and 1.6MB of RAM, the
HD-tree reaches its optimal status where each leaf
node occupies only one disk block. In Figure 8, more
RAM to the HD-tree is served as a cache which is
the same as that of the Prefix B-tree. It is shown that
the HD-tree is continually better than the Prefix B-
tree when the RAM is largely available. In Figure 9,
we compare the number of I/Os for different query
lengths. It is shown that the HD-tree performs in-
creasingly better than the Prefix B-tree as the query
string length increases. Since the Prefix B-tree uses
the same amount of RAM as that of the HD-tree to
cache internal nodes, we conclude that the hybrid
RAM/disk-based index structure (e.g., the HD-tree)
is better than the disk-based structure combined with
caching (e.g., the Prefix B-tree plus LRU caching),
especially when queries are more distinctive.
2 3 4
5 6
7
8 9
Average Query String Length
1
10
100
1000
Number of Disk I/Os per Query
HD-tree
Prefix B-tree
Figure 9: I/O comparison for different query lengths; y-axis
is in Logarithmic scale.
Finally, we compared the HD-tree with the Prefix
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
120
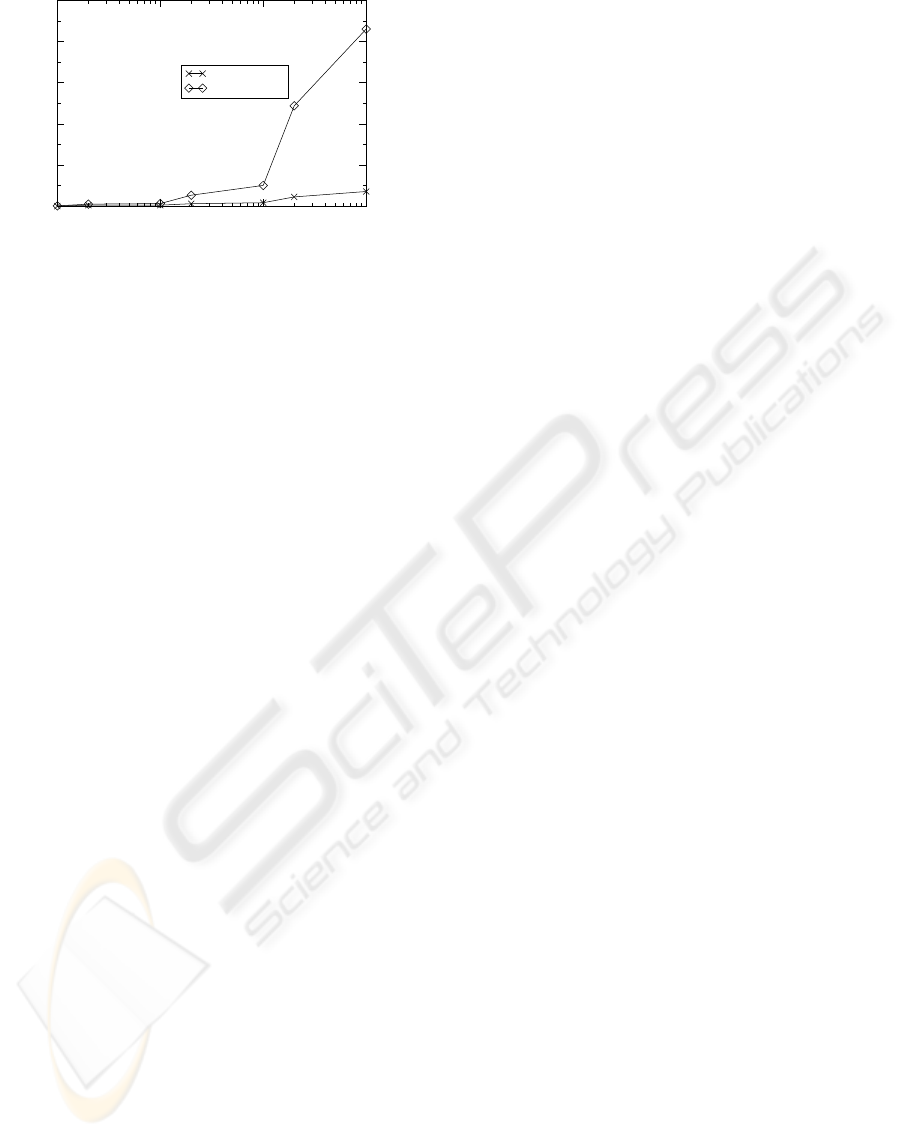
1 10 100 1000
Number of Distinctive Queries
25
50
75
100
125
Total Running Time (seconds)
HD-tree
Prefix B-tree
Figure 10: Running time comparison; average query string
length is 6.
B-tree in terms of total running time including both
the RAM processing time and the I/O time. The
experiments were conducted in the same computing
environment (a Linux PC with 512MB RAM and
1.8GHz Pentium 4 processor). Figure 10 shows the
running time of the HD-tree and the Prefix B-tree
for 1000 queries with different numbers of distinc-
tive queries. We notice that the actual running time of
the HD-tree is comparable to that of the Prefix B-tree
even when the 1000 queries are the same. The rea-
son is that with a large amount of RAM available, the
operating system provides LRU caching for the HD-
tree as well. The HD-tree is shown to be increasingly
faster than the Prefix B-tree as the number of distinc-
tive queries increases. For 1000 distinctive queries,
the HD-tree is more than one magnitude faster than
the Prefix B-tree.
4 CONCLUSION
There is an increasing demand for efficient index-
ing techniques to support various types of queries
on large string databases. Most existing string in-
dexing techniques are either RAM-based or disk-
based. RAM-based index structures are not suitable
for string matching queries on large databases when
only a limited amount of RAM is available. Disk-
based structures, on the other hand, can index large
databases but usually do not fully utilize the available
RAM.
The HD-tree is proposed as a novel hybrid
RAM/disk-based structure, taking advantage of the
strengths of both RAM-based and disk-based struc-
tures. The HD-tree not only scales well with the sizes
of the RAM and the database, but also is efficient
for various types of queries. The experimental results
show that the HD-tree outperforms the Prefix B-tree
for prefix and substring searches. For random distinc-
tive queries, the number of disk I/Os is reduced by a
factor of two to three, while the running time is re-
duced in an order of magnitude. Therefore, we con-
clude that a hybrid RAM/disk-based index structure
such as the HD-tree is promising for supporting effi-
cient searches in large string databases whose indexes
cannot fit entirely in the RAM.
REFERENCES
Baeza-Yates, R. and Ribiero-Neto, B. (1999). Modern In-
formation Retrieval. Addison Wesley Longman Pub-
lishing Co. Inc.
Bayer, R. and McCreight, E. M. (1972). Organization and
maintenance of large ordered indexes. Acta Informat-
ica, 1(3):173–189.
Bayer, R. and Unterauer, K. (1977). Prefix b-trees. ACM
Trans. Database Syst., 2(1):11–26.
Clark, D. R. and Munro, J. I. (1996). Efficient suffix trees on
secondary storage. In Proceedings of the seventh an-
nual ACM-SIAM symposium on Discrete algorithms,
pages 383–391, Atlanta, Georgia, United States. Soci-
ety for Industrial and Applied Mathematics.
Comer, D. (1979). Ubiquitous b-tree. ACM Comput. Surv.,
11(2):121–137.
Fagin, R., Nievergelt, J., Pippenger, N., and Strong, H. R.
(1979). Extendible hashing a fast access method for
dynamic files. ACM Trans. Database Syst., 4(3):315–
344.
Ferragina, P. and Grossi, R. (1999). The string b-tree: A
new data structure for string search in external mem-
ory and its applications. J. Assoc. Comput. Mach.,
46(2):236–280.
Gonnet, G. H., Baeza-Yates, R. A., and Snider, T. (1991).
Lexicographical indices for text: Inverted files vs. pat
trees. Technical Report OED-91-01, University of
Waterloo.
Manber, U. and Myers, G. (1990). Suffix arrays: a new
method for on-line string searches. In Proceedings
of the first annual ACM-SIAM symposium on Discrete
algorithms, pages 319–327. Society for Industrial and
Applied Mathematics.
McCreight, E. M. (1976). A space-economical suffix tree
construction algorithm. J. ACM, 23(2):262–272.
Morrison, D. R. (1968). Patricia practical algorithm to re-
trieve information coded in alphanumeric. J. ACM,
15(4):514–534.
Sleepycat (2004). Berkeley db. http://www.sleepycat.com/.
Voorhees, E. M. and Harman, D. (1997). Overview of the
sixth text retrieval conference (trec-6). In Proceedings
of the Sixth Text REtrieval Conference, pages 1–24.
NIST Special Publication.
Weiner, P. (1973). Linear pattern matching algorithms. In
14th Annual Symposium on Switching and Automata
Theory, pages 1–11. IEEE.
Xue, Q., Pramanik, S., Qian, G., and Zhu, Q. (2004). The
hybrid ram/disk-based index structure. Technical re-
port, Department of CSE, Michigan State University.
THE HYBRID DIGITAL TREE: a new indexing technique for large string databases
121
