IMPLEMENTATION OF A HYBRID INTRUSION DETECTION
SYSTEM USING FUZZYJESS
Aly El–Semary, Janica Edmonds, Jes
´
us Gonz
´
alez and Mauricio Papa
Center for Information Security, University of Tulsa
600 S. College Av., Tulsa, OK, 74104
Keywords:
Fuzzy logic, data mining, intrusion detection.
Abstract:
This paper describes an implementation of a fuzzy inference engine that is part of a Hybrid Fuzzy Logic
Intrusion Detection System. A data-mining algorithm is used offline to capture features of interest in network
traffic and produce fuzzy-logic rules. Using an inference engine, the intrusion detection system evaluates
these rules and gives network administrators indications of the firing strength of the ruleset. The inference
engine implementation is based on the Java Expert System Shell (Jess) from Sandia National Laboratories and
FuzzyJess available from the National Research Council of Canada. Examples and experimental results using
data sets from MIT Lincoln Laboratory demonstrate the potential of the approach.
1 INTRODUCTION
A significant challenge in providing an effective de-
fense mechanism to a network perimeter is detecting
intrusions and implementing countermeasures. Com-
ponents of the network perimeter defense capable of
detecting intrusions are referred to as Intrusion De-
tection Systems (IDS). Typically, an IDS uses boolean
logic in determining whether or not an intrusion is de-
tected. More recently, the use of fuzzy logic (Zadeh,
1984) (Zadeh, 1988) has been investigated as an alter-
native to boolean logic in the design and implementa-
tion of these systems. Fuzzy logic techniques have
been successfully employed in the computer security
field since the early 90’s (Ovchinnikov, 1994) and
provides a sound foundation to handle imprecision
and vagueness as well as mature inference mecha-
nisms using varying degrees of truth (Hosmer, 1993).
Because boundaries are not always clearly defined,
fuzzy logic can be used to identify patterns or behav-
ior variations (Gomez and Dasgupta, 2002). This is
accomplished by building an IDS that combines fuzzy
logic rules with an expert system capable of evaluat-
ing rule truthfulness. This combination results in an
IDS capable of applying fuzzy logic reasoning to in-
coming data streams. Our approach uses an optimized
deterministic algorithm together with a preprocessor
to help reduce the amount of data that needs to be an-
alyzed by the inference engine.
IDS
output
records
packets
Preprocessor
Data Miner
Fuzzy Inference
Engine
rules
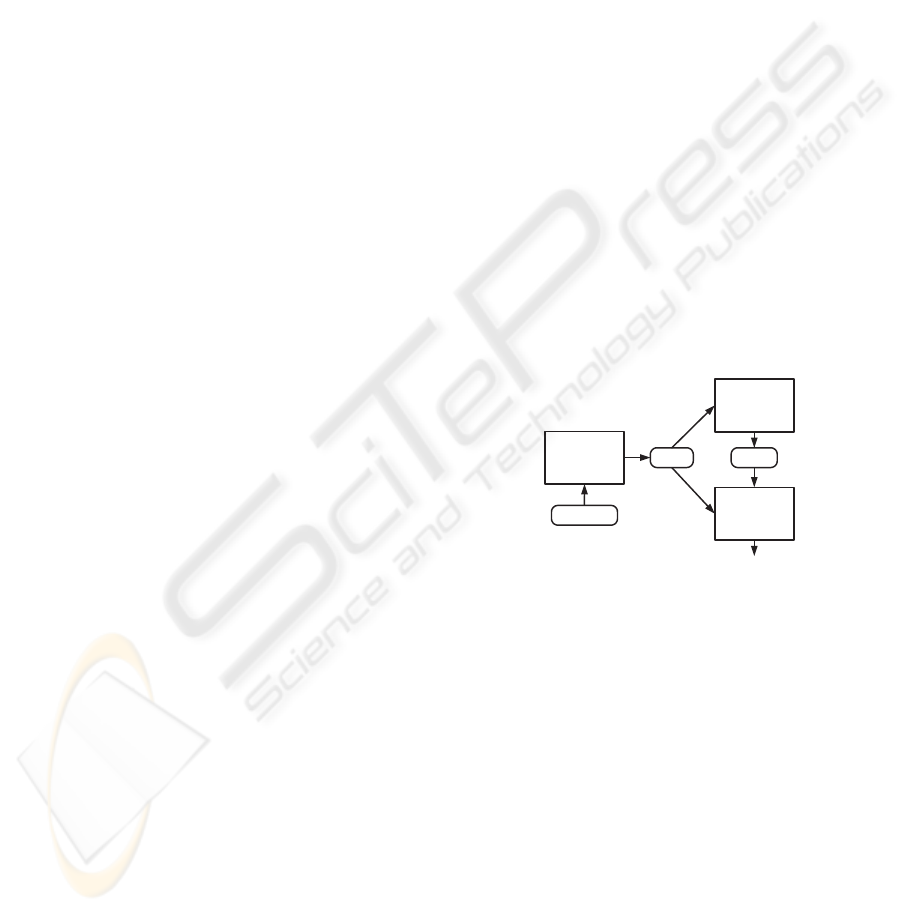
Figure 1: System Architecture
2 ARCHITECTURE
The Hybrid Fuzzy Logic IDS architecture (see Fig-
ure 1) has two modes of operation: rule–generation
and detection. When operating in the rule–generation
mode, the system processes network data and uses a
fuzzy data mining algorithm to generate rules. A sub-
set of the rules produced by the data mining algorithm
is used as a model for the input data. The detection
mode uses this rule subset for intrusion detection.
The Preprocessor is responsible for accepting raw
packet data and producing records. This component is
used in both modes and is capable of reading packets
from the wire or a tcpdump file. The output consists
of records, each containing aggregate information for
390
El–Semary A., Edmonds J., González J. and Papa M. (2005).
IMPLEMENTATION OF A HYBRID INTRUSION DETECTION SYSTEM USING FUZZYJESS.
In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 390-393
DOI: 10.5220/0002524203900393
Copyright
c
SciTePress

each packet group. Using records and concentrating
only on attributes of interest greatly helps in reducing
the amount of information used by more computation-
ally intensive components of the architecture. Specif-
ically, records (and not packets) are used by the infer-
ence engine in our system to evaluate fuzzy rules.
The Data Miner implements a variation of Kuok’s
(Kuok et al., 1998) algorithm that allows for efficient,
single-pass, record processing by partioning data into
hierarchical files to produce output rules. Candidate
rules are expressed in terms of itemsets, a grouping
of relevant attributes. In order to minimize the poten-
tially large number of candidate rules, the algorithm
uses the concept of large itemsets to maximize the ex-
pressive power of the rule. Our implementation inte-
grates the Apriori and Kuok’s algorithms and is capa-
ble of discovering association rules for binary, cate-
gorical and numerical attributes. The final output of
the algorithm is a set of fuzzy rules. Rules are ex-
pressed as a logic implication p → q where p is the
antecedent and q is the consequence.
The fuzzy inference engine implements fuzzy logic
reasoning to evaluate the truthfulness of the incoming
records against the rules produced by the Data Miner.
Its implementation is the focus of this paper and a
more detailed description follows.
3 IMPLEMENTATION
The Fuzzy Inference Engine (Figure 1) makes use
of FuzzyJess (Orchard, 2001), a rule based expert
system shell that integrates the functionality of the
FuzzyJ Toolkit (Orchard, 2001) with Jess (Friedman-
Hill, 2004). The FuzzyJ Toolkit allows the expression
of fuzzy reasoning within the Java environment and
Jess provides a Java-based rule-engine in which rules
can be applied to data.
Jess, the Java expert system shell and scripting
language developed by Sandia National Laboratories,
can be used as either a general-purpose programming
language or as a rule-engine to efficiently apply rules
to data. Rule-based expert systems developed in Jess
can be firmly linked to Java code. Jess rules allow
for reasoning about knowledge that is expressed as
facts. These facts and rules, though, cannot handle
the imprecision and uncertainty that often abounds in
real-life applications.
The National Research Council of Canada devel-
oped The FuzzyJ Toolkit, a Java API that extends
Jess to allow reasoning about some forms of uncer-
tainty through the use of fuzzy sets and fuzzy rea-
soning. Fuzzy concepts are represented in the FuzzyJ
Toolkit using the keywords FuzzyVariable, Fuzzy-
Set, and FuzzyValue. A FuzzyVariable describes
a general fuzzy concept (Zadeh, 1975). It consists
Membership
TCP
0.25
0.00
1.00
0.6 1.0
Above
Average
0.20.0
Average
Below
Average
0.70
Figure 2: Fuzzy variable
of a name (T CP ), its units (N umberofP ackets), a
range ([0, 100]), and a set of terms that describe spe-
cific fuzzy concepts for this variable. These fuzzy
terms are defined using a term name (Average or
AboveAverage) together with a fuzzy set.
A FuzzySet (Zadeh, 1965) identifies the degree of
membership of the term over the range of the fuzzy
variable. Figure 2 illustrates the use of fuzzy sets
to describe the fuzzy variable T CP over [0,1] using
three fuzzy term sets. Thus, the fuzzy variable T CP
is a measure of the number of TCP packets received
within a certain time frame. All values that T CP can
assume must fall into at least one of those fuzzy sets.
Membership functions (Zadeh, 1965) map each ob-
ject in the fuzzy set to a real number in the inter-
val [0,1]. Fuzzy membership functions are used to
evaluate degrees of membership for each category or
term. Thus, the membership function f
A
(x) produces
a value that indicates the truth value of x in the term
A. For instance, in Figure 2, f
BelowAverage
(0.2) =
70% indicates that a T CP value of 0.2 belongs to
BelowAverage with 70% certainty.
A FuzzyValue represents a specific fuzzy concept.
The logic of the expert system is expressed in terms of
FuzzyRules. A FuzzyRule holds three sets of Fuzzy-
Values representing the antecendents, consequences,
and input values of the rule. The antecedents must be
true before the rule can execute (or fire) and conse-
quences asserted. An example of a fuzzy rule is
if TCP is
Average
then SYN is
Average
For this rule to fire the T CP value needs only to
match the fuzzy concept of Average to some degree
for the antecedent to be true.
Simple fuzzy systems can be created quite easily
using the FuzzyJ Toolkit, but larger systems with a
greater number and type (fuzzy, crisp, fuzzy-crisp) of
rules suggest that a convenient way to encode many
types of applications is needed. FuzzyJess is a rule
based expert system shell that integrates the fuzzy
logic of the FuzzyJ Toolkit with Jess to provide a
more robust tool for fuzzy reasoning. The Fuzzy In-
ference Engine is implemented using FuzzyJess.
The Fuzzy Inference Engine can be used with sam-
ple offline data or live traffic. Use of sample data (read
IMPLEMENTATION OF A HYBRID INTRUSION DETECTION SYSTEM USING FUZZYJESS
391

p qfuzzy match
no fuzzy match
fuzzy match
no fuzzy match
firing
strength =
minimum
firing
strength of
p and q
firing strength = 0firing strength = 1
Figure 3: Analysis of fuzzy rules
as records) is useful to test the system and evaluate the
validity of the rule base.
The three inputs to the Fuzzy Inference Engine are
1) the configuration parameters that FuzzyJess uses
to define the FuzzyVariables; 2) the rules produced
by the Data Miner; and 3) the records, which are as-
serted as facts in FuzzyJess. The three term functions
of
Below Average, Average,
and
Above Average
were
defined for each fuzzy variable using the parameters
in the configuration file. The definitions made use
of functions within FuzzyJess as indicated:
Below
Average
: uses RightLinearFuzzySet,
Average
: uses
TrapezoidFuzzySet, and
Above Average
: uses Left-
LinearFuzzySet. The Fuzzy Inference Engine uses
FuzzyJess to determine the firing strength of each rule
applied to each fact. FuzzyJess can be configured
to use Mamdani or Larsen inference mechanisms to
compute output. The evaluation of rules (see Figure
3) begins with the analysis of the antecedent, p. The
following cases for p:
• p does not have a fuzzy match so the rule does not
apply to the record and the firing strength is one
• p does have a fuzzy match and the analysis of the
consequence q begins
Note that a fuzzy match occurs when the truth value
of the predicate is greater than zero. Similarly, the
following cases are considered for the consequence q:
• q does not have a fuzzy match and the firing
strength of the rule is zero
• q has a fuzzy match and the firing strength of
the rule is determined using Mamdani’s inference
mechanism.
Fuzzy rules, as produced by the data mining algo-
rithm, model a behavior represented by the data set
employed to run the algorithm. The output of the
Fuzzy Inference Engine is the firing strength of each
rule for a given fact. This firing strength determines
whether or not the fact satisfies the modeled behavior.
Firing strengths that have a value close to one indi-
cate that observed behavior closely follows the mod-
eled behavior, but when several facts register firing
strengths at or close to zero for a given rule, then it
is likely that a deviation from the model has been de-
tected (a potential attack).
Membership
TCP
0.00
1.00
0.157 1.0
Above
Average
0.0
Average
Below
Average
0.50
0.8750.424
Figure 4: TCP fuzzy definition
Membership
SYN
0.00
1.00
0.003 1.0
Above
Average
Average
Below
Average
0.50
0.8750.298
Figure 5: SYN fuzzy definition
4 ANALYSIS
The following examples illustrate how three records
are processed and rules evaluated by the Fuzzy Infer-
ence Engine. Consider the following rule:
if TCP is
Average
then SYN is
Average
where the
Average
membership function may be de-
fined differently for each attribute. The input records
for the Fuzzy Inference Engine contain values for
each attribute in the form of {TCP, SYN}. The first
record is {0.591, 0.372}. The Fuzzy Inference En-
gine evaluates the first record against the rule by be-
ginning with the antecedent; from Figure 4 we ob-
serve that T CP
Average
(0.591) = 0.6297. Once the
antecendent has been evaluated and has a truth value
greater than 0.0, then the consequence is evaluated:
SY N
Average
(0.372) = 0.8718 (see Figure 5). Thus,
this rule has a firing strength of 0.6297 for this record.
The second record is {0.011, 0.013}. Evalua-
tion of the antecedent shows T CP
Average
(0.011) =
0.0. Thus, the rule does not fire, the consequence
is not analyzed, and the firing strength of the rule
is 1.0 for this record. The third record is {0.266,
0.895}. Therefore, T CP
Average
(0.266) = 1.0 but
SY N
Average
(0.895) = 0.0. Thus, the truth value of
the rule for this record is 0.0.
The Fuzzy Inference Engine is used to analyze sets
of data and the training data used in our experiments
correspond to the 1999 DARPA Intrusion Detection
offline evaluation (Haines et al., 1999) data set as pro-
vided by Lincoln Laboratory (MIT, 1999). Data for
this experiment was taken during an ipsweep (pings
on multiple host addresses) attack. More specifically,
ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
392

Figure 6: Rule output detects ipsweep attack
the traffic seen from 4:00 pm to 5:00 pm of the fourth
day of the second week. The attack begins at 4:36pm.
For the next 5 minutes at least one ping request packet
is made from an outside network to each host on an
internal segment of the network. This scan drasti-
cally increases the number of ICMP packets in the
attack time interval. The Preprocessor produced ap-
proximately one record per second of data resulting
in 3570 records from all of the packets sent during
this specific time frame.
The Data Miner produced 31 rules with a 95%
confidence value when inspecting normal traffic data,
which were sent to the Fuzzy Inference Engine. Note
that since these rules model normal behavior, i.e., at-
tack traffic was not used by the Data Miner, the sys-
tem serves as an anomaly-based IDS. The Fuzzy In-
ference Engine compared each record against all of
the rules and output a listing of the firing strengths
of each rule for each record. These firing strengths
are used to determine the likelihood that an attack is
in process. It took the Fuzzy Inference Engine about
13 minutes to evaluate 3570 records against 31 rules.
Thus, it took about 13 minutes to evaluate 60 minutes
of offline data. Our current implementation is capa-
ble of handling real-time data using using time win-
dows (records) in the order of milliseconds. Clearly,
smaller time windows would result in greater Fuzzy
Inference Engine times as the number of records to
be evaluated increases.
Figure 6 shows the firing strength of Rule 2 for at-
tack data (solid line). In light grey, a count of recent
records with firing strength below a value of 0.5 is
used to provide additional feedback. It is clear from
Figure 6 that this rule evidences an attack starting
around record 2,100 (see increasing counter value).
5 CONCLUSION
FuzzyJess proved to be an invaluable tool during our
implementation of a Hybrid Fuzzy Logic Intrusion
Detection system. It saved invaluable implementation
time by providing an efficient inference engine that
could be easily integrated into our code base. Experi-
mental results show that the amount of time required
to process a relatively large number of records against
a set of rules allows this prototypical IDS to be used
in a real-time environment (for reasonably small time
windows). Optimization of the Fuzzy Inference En-
gine implementation would provide even faster analy-
sis times and quicker attack detection by opening the
door to new analysis and visualization techniques.
Future work will also concentrate on identifying sets
of relevant attributes that will allow detection of a
wide variety of attacks.
REFERENCES
Friedman-Hill, E. J. (2004). Jess, the java expert system
shell. In http://herzberg.ca.sandia.gov/jess. Sandia
National Laboratories.
Gomez, J. and Dasgupta, D. (2002). Evolving fuzzy clas-
sifiers for intrusion detection. In 3rd Annual Informa-
tion Assurance Workshop. West Point, NY.
Haines, J., Lippmann, R., Fried, D., Tran, E., Boswell, S.,
and Zissman, M. (1999). 1999 darpa intrusion detec-
tion system evaluation: Design and procedures. In
MIT Lincoln Laboratory Technical Report.
Hosmer, H. A. (1993). Security is fuzzy! applying the fuzzy
logic paradigm to the multipolicy paradigm. In 1992-
93 workshop on New Secuity Paradigms. Little Comp-
ton, RI.
Kuok, C., Fu, A., and Wong, M. (1998). Mining fuzzy as-
sociation rules in databases. In The ACM SIGMOD
Record. Vol. 27, No. 1.
MIT (1999). Lincoln laboratory data sets. In
http://www.ll.mit.edu/IST/ideval/data/1999.
Orchard, R. (2001). Fuzzy reasoning in jess: The fuzzyj
toolkit and fuzzyjess. In ICEIS 2001, 3rd Interna-
tional Conference on Enterprise Information Systems.
Setubal, Portugal.
Ovchinnikov, S. (1994). Fuzzy sets and secure computer
systems. In Workshop on New security paradigms.
Little Compton, RI.
Zadeh, L. A. (1965). Fuzzy sets. In Information and Con-
trol. Vol. 8, Num. 3.
Zadeh, L. A. (1975). The concept of a linguistic variable
and its application to approximate reasoning, parts 1,
2, and 3. In Information Sciences.
Zadeh, L. A. (1984). Making computers think like people.
In Spectrum. IEEE.
Zadeh, L. A. (1988). Fuzzy logic. In IEEE-CS Computer.
Vol. 21, Num. 4.
IMPLEMENTATION OF A HYBRID INTRUSION DETECTION SYSTEM USING FUZZYJESS
393
