
A DECISION SUPPORT SYSTEM BASED ON NEURO-FUZZY
SYSTEM FOR RAILROAD MAINTENANCE PLANNING
Michele Ottomanelli
Dept. of Environmental Engineering and Sustainable Development, Technical University of Bari
Viale del Turismo, 8 – 74100 Taranto, Italy
Mauro Dell’Orco, Domenico Sassanelli
Dept. of Highways and Transportation, Technical University of Bari, Italy
Via Orabona, 4 – 70125 Bari, Italy
Keywords: Decision Support Systems, Neuro-Fuzzy, Railroad Maintenance
Abstract: Optimization of Life Cycle Cost (LCC) in railroad m
aintenance, is one of the main goals of the railways
managers. In order to achieve the best balance between safety and operating costs, “on condition”
maintenance is more and more used; that is, a maintenance intervention is planned only when and where
necessary. Nowadays, the conditions of railways are monitored by means of special diagnostic trains: these
trains, such as Archimede, the diagnostic train of the Italian National Railways, allow to observe every 50
cm dozens of rail track characteristic attributes simultaneously. Therefore, in order to plan an effective on
condition maintenance, managers have a large amount of data to be analyzed through an appropriate
Decision Support System (DSS). However, even the most up-to-date DSSs have some drawbacks: first of
all, they are based on a binary logic with rigid thresholds, restricting their flexibility in use; additionally,
they adopt considerable simplifications in the rail track deterioration model. In this paper, we present a DSS
able to overcome these drawbacks. It is based on fuzzy logic and it is able to handle thresholds expressed as
a range, an approximate number or even a verbal value. Moreover, through artificial neural networks it is
possible to obtain more likely the rail track deterioration models. The proposed model can analyze the data
available for a given portion of rail-track and then it plans the maintenance, optimizing the available
resources.
1 INTRODUCTION
This study is addressed to tamping operation in
railways maintenance. It is compacting and forcing
the ballast against the rails and sleepers. Such an
operation is frequently carried out by railways
companies, with the exception of the new slab
tracks, where the ballast is substituted by concrete or
asphalt slab.
The aim of the tamping is to improve geometrical
p
arameters of the railway track such as alignment,
longitudinal level, super-elevation, gauge and
buckling, to reach a higher safety level of the
railway.
A variety of mechanical (a
utomated) tamping device
are available: they are able to tamp ballast under 2 or
3 sleepers at the same time, thus it is possible to
tamp up to 2200 meters of track per hour.
We have to point out that frequently repeated
t
amping operations could cause negative effect for
the ballast. In particular, with respect to the effect on
the ballast aging, each tamping cycle is equivalent to
a 20 Megatons (MGT) of cumulate traffic, due to
increasing of the finer material percentage.
During the life cycle, a given track shows three
d
ifferent phases with respect to the capacity of
preserving its original geometrical and
morphological characteristics.
For example, let us assume as track quality index a
p
arameter that shows the deterioration of the
geometrical layout, such as the standard deviation
(SD) of the track alignment. In Figure 1 such a
parameter has been connected to the traffic,
43
Ottomanelli M., Dell’Orco M. and Sassanelli D. (2005).
A DECISION SUPPORT SYSTEM BASED ON NEURO-FUZZY SYSTEM FOR RAILROAD MAINTENANCE PLANNING.
In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 43-49
DOI: 10.5220/0002524500430049
Copyright
c
SciTePress
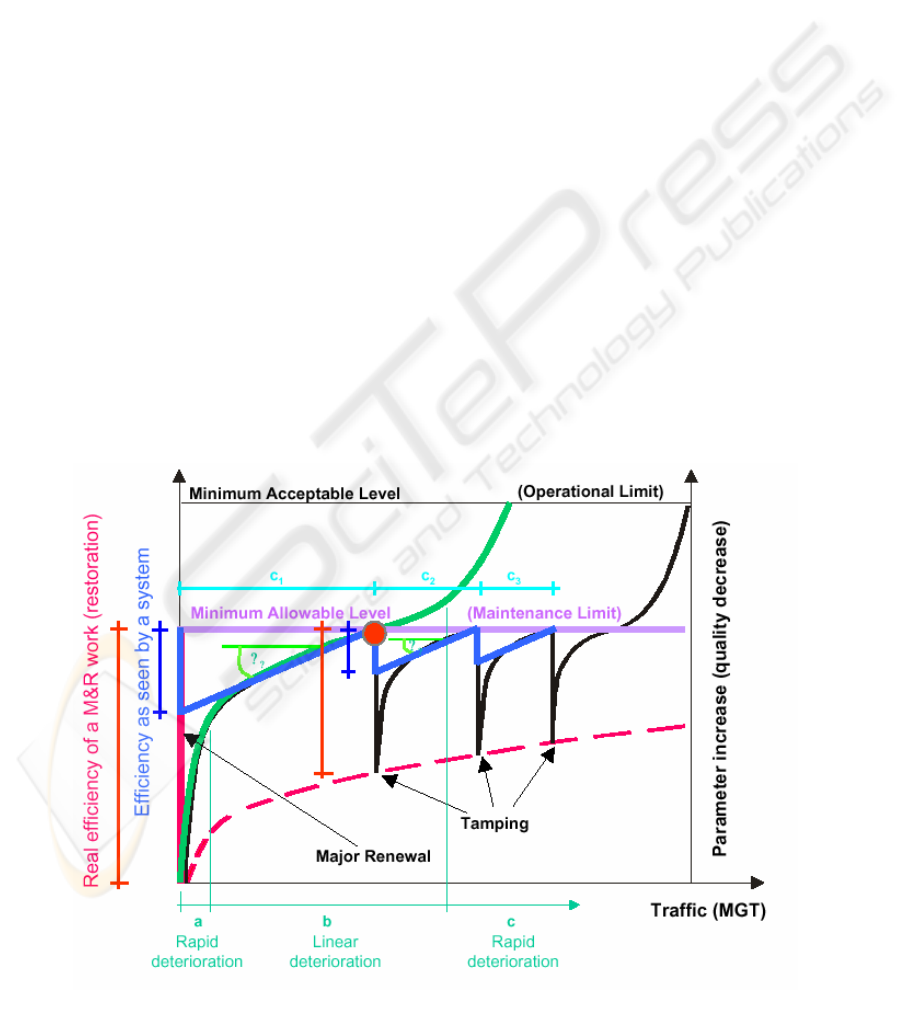
expressed in MGT of trains load, accumulated from
the track operation starting. The aging curve is made
up of three sections: two are curvilinear and one
usually is quasi-linear. The aging curve represents
the behaviour of the track when no maintenance
operations are carried out.
The first portion (a) of the curve is the youth phase
of the track and it shows a quick increase of the SD,
due to an early track settling: the higher SD value is
the lower is the ballast compactness. It is very
difficult to foresee how long the youth phase lasts
since it depends on a number of factors. Moreover,
such a phase could be affected also by the part of the
railway track we are not dealing with.
The second phase, usually known as intermediate
phase, is represented by a less than linear curve part
(b). This phase starts when the track settling is near
to be completed and, consequently, the track aging
ratio can be assumed as constant. The intermediate
phase lasts for most of the track lifetime; for this
reason and for sake of computing simplicity, a lot of
algorithms consider only this part of the track
lifetime.
The last phase (old phase) is representative of the
tracks near to the end of the life-time. This curve
section (c) shows a quick aging of the track: the
value of SD increases in approximately as in
exponential way. Generally, in order to preserve
railway safety through proper maintenance
operations, this phase should be avoided.
Dashed line in figure 1 represents the lower bound
of SD, that is the maximum improvement that can be
obtained for the track through tamping operations.
From the same figure it is possible to note that
effectiveness of tamping decreases as the aging of
the track increases; thus, starting from a certain time,
it should be more economical to renew ballast, rails
or sleepers than carrying out tamping operations
since they would become more frequent and less
effective.
Existing Decision Support Software (DSS), such as
Ecotrack, usually has the following drawbacks:
a) the phases a and c are not taken into account,
thus the aging function is assumed to be linear
for the whole life-time of the track;
b) the considered aging function is assumed to be
the same for the whole rail track;
c) such models assume as intervention thresholds
some rigid and crisp values.
Actually, the approximation imbedded in the point
1) is not suitable from the safety standpoint. In fact,
because of several different reasons such as bad
maintenance programs or problems concerning local
conditions of the superstructure or roadbed, the track
deterioration could be quicker than linear. In this
case, the thresholds should be crossed sooner than
the DSS foresaw.
In figure 2 such a situation is depicted referring to a
200m long track segment. Track alignment was
observed each 50 cm, then 400 observations are
Figure 1: Aging Function
ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
44
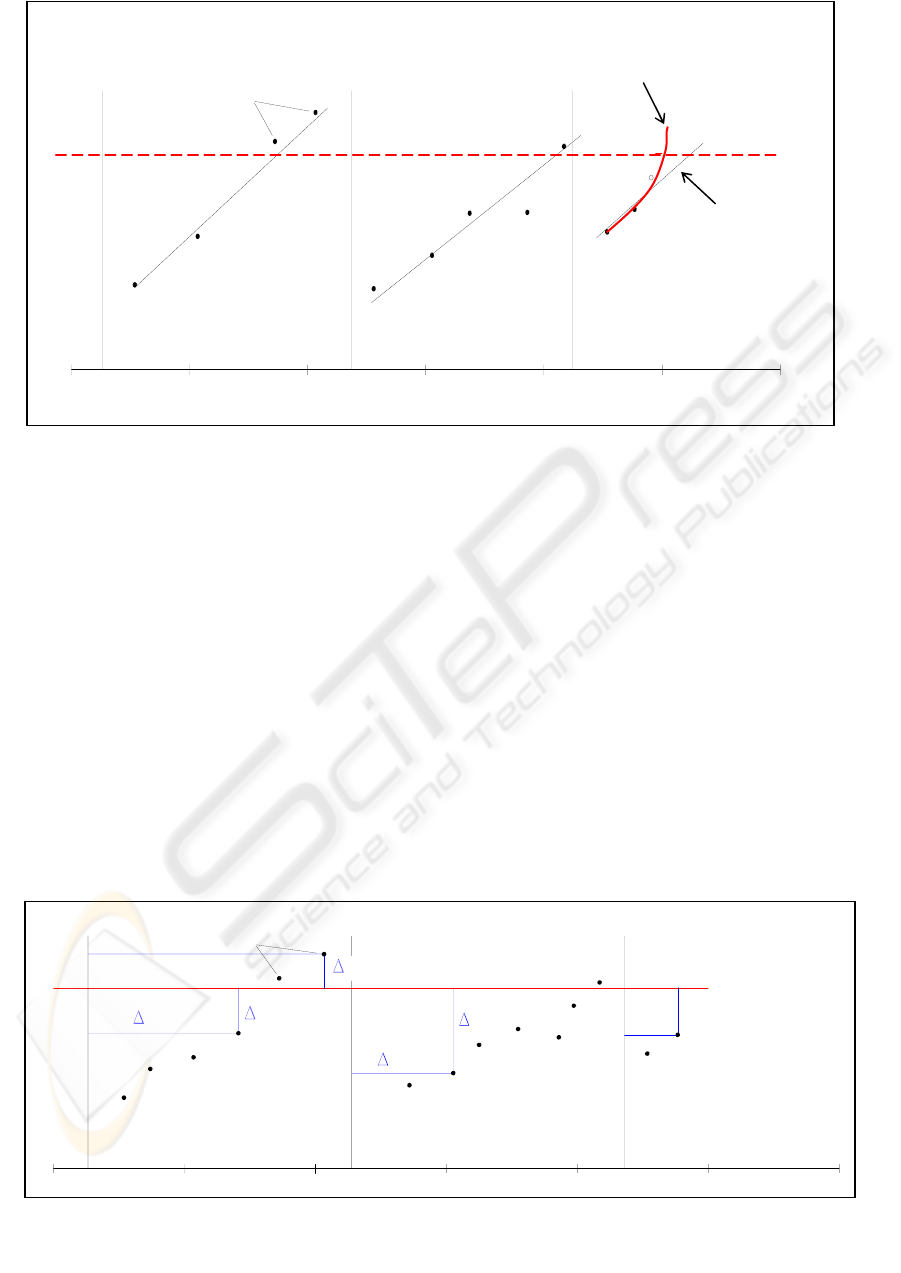
Actual trend
Above-threshold
values
T1 T2
T3
available for each segments: on the basis of the
observed values, the DSS determines the Standard
Deviation (SD). The ordinates represent the value of
SD for the alignment with respect to time. The
vertical lines T1, T2 e T3 represents the tamping that
have been carried out in the last years. The
horizontal dashed line represents the threshold value
suggested by the European Rail Research Institute
(ERRI) for the acceptability of the observed
parameter.
From the figure 2, it is possible to see that linear
extrapolation of SD can mislead, since in case the
track-segment is in its old phase -as frequently
happens in reality, the date for tamping maintenance
would be later than necessary.
Concerning the statement 2), it has to be pointed out
that different track-segments usually have different
geometrical deterioration trend and different wear
and tear of the rails, even under the same load
conditions.
European railways companies have widely verified
this issue, thus the general three-phases shape of the
aging function (figure 1) should to be adjusted for
each track-segment in order to take into account
local characteristics of the track.
The issue in the statement 3) has got conceptual
origin. Traditional DSS’s are quite rigid, since they
assume crisp values for the thresholds: as the
observed parameter exceed the threshold, the
decision rule suggests maintenance. An example of
this kind of rule could be:
IF (SDalignment > 1.4) THEN tamping
Figure 2: Example of incorrect extrapolation
1997
1999
Threshold value
2001
12
Linear trend
Reference time
T1 T2
T3
SD
(<0)
P
19981997
Over threshold values
1999
days
SD (>0)
20012000
threshold
days
2002 2003
SD
∆SD
∆days
Figure 3: Scheme of the variation of quality indexes.
A DECISION SUPPORT SYSTEM BASED ON NEURO-FUZZY SYSTEM FOR RAILROAD MAINTENANCE
PLANNING
45
This approach does not allow to take into account
how much the threshold has been exceeded; in fact,
such a DSS gives the same importance to very
different values of the SD, for example 1.4 and 3.0.
In other words, it gives the same importance when
the SD of the parameter exceeds “very slightly” or
“heavily” the given threshold.
low-medium
low
medium
medium-high
hi
g
2 METHODOLOGY
In order to overcome some of the mentioned
drawbacks of traditional DSS, in this paper we
propose a new methodology based on an Adaptive
Network-based Fuzzy Inference System (ANFIS).
Using the proposed ANFIS algorithm, it is possible
to calibrate the Membership Functions (MF) of the
Fuzzy Inference System (FIS), with reference to a
given track-segment. Subsequently, the results
obtained by the proposed model have been
compared to those obtained by using Ecotrack.
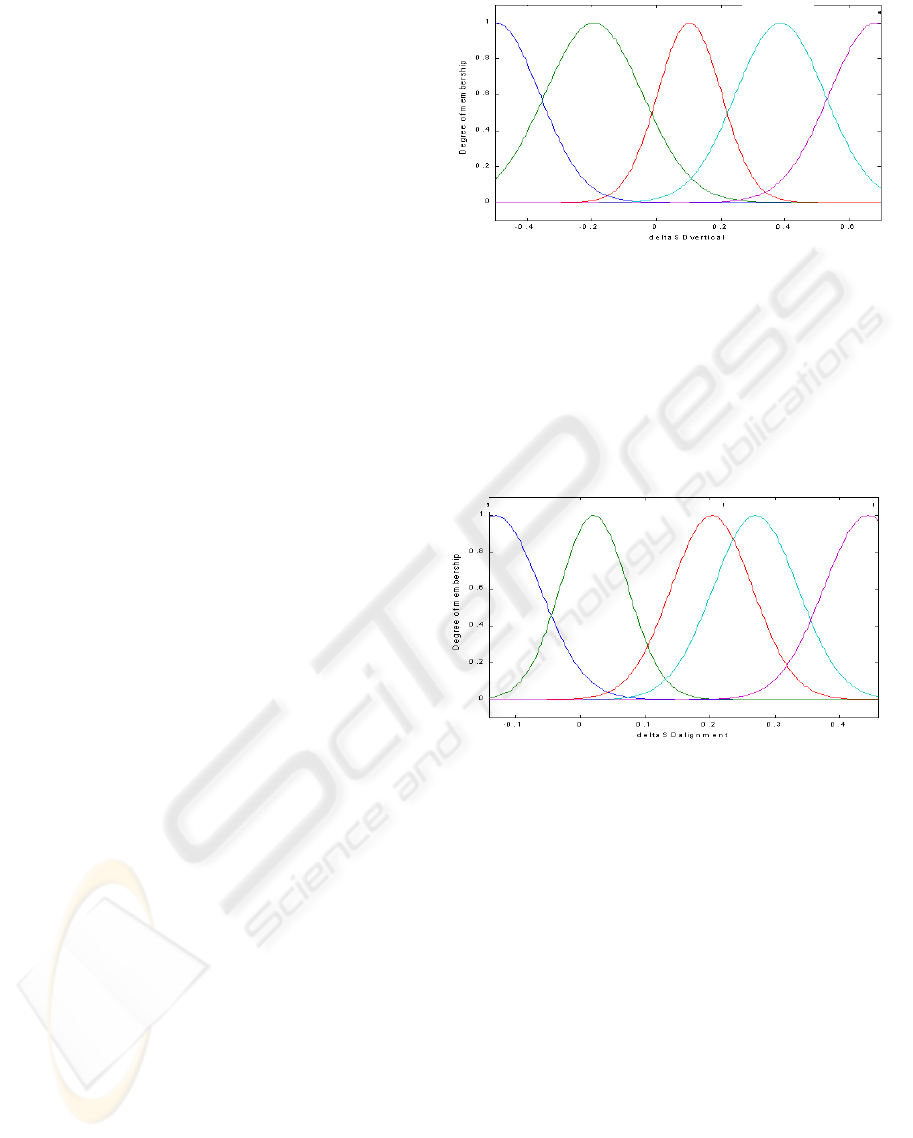
Figure 5: Membership function for ∆SDvertical
To test the robustness of the two DSS, we also
simulate some rough errors in data observation.
The FIS has been applied to 200 m long track-
segment. In figure 3 is the scheme of changes in
time of the track-segment quality indexes. The
proposed Fuzzy Inference System has been specified
with three input elements and one output element; in
particular as input elements we have considered the
SD of alignment, the SD of vertical level and the
number of days past from last tamping. As output
the FIS provides with an estimate of the date for
tamping works on the track-segment.
The Standard Deviations of the two input parameters
have been represented through the following five
Gaussian Membership Functions (MF):
low, low-medium, medium, medium-high, high.
The output is made up of singletons, indicating the
number of days, starting from the date of the
analysis, before the next tamping.
The time period “Ddays” is the number of days
between the tamping carried out straight before each
measurement and the date of the survey P, while
DSD
alignment
and DSD
vertical
are respectively the
differences between given threshold values and the
SD of alignment and the SD of longitudinal level. It
is evident that, if the threshold value is exceeded, the
differences DSD reach negative values.
Such a FIS has been calibrated through an ANFIS
algorithm: all the MFs have been calibrated by
training the Artificial Neural Network (ANN)
relevant to the FIS. The structure of the adaptive
ANN is chosen by the analyst, which chooses also
the number of MF to be associated to each input and
output. The ANN represents an analytical tool able
to learn and emulate the behaviour of a real system.
The ANN for a given time interval operates side by
side with the real system (training phase) and
modifies its characteristics until the error done is
minimised. The characteristics of the ANN of the
given ANFIS, such as input and output nodes and
the number hidden layers are relevant to the FIS.
Given a certain number of input−output pairs, the
error ε is the difference between the output value Y*
determined by the ANN and the “true” output value
Y (so-called “pattern”):
low-medium
low
medium medium-high high
Figure 4: Membership function for ∆SDalign.
ε = |Y* -Y| (1)
The characteristics of an adaptive ANN are the node
functions, which correspond to the MF of the FIS.
Those functions are to be calibrated during the
training phase. The node functions correspond to the
Membership Functions of the FIS referring to; such
a functions are calibrated during the training phase.
3 MODEL SPECIFICATION AND
CALIBRATION
To carry out the specification and calibration of the
proposed model, a 200 m long track-segment has
ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
46

been considered. The following features were
available for this segment:
– maximum speed of the railway line 140 km/h;
– laying date for all components of the track, like
ballast, rails, sleepers and fastenings, 1/1/1985;
– during the period February 1992 - July 2002, ten
measurements a year for SD alignment and SD
vertical level have been carried out;
– in the same period, three tamping have been
carried out, namely in January ‘92, August ‘96,
October 2001;
– the period from 1/1/2003 to 31/12/2007 has been
considered as planning period.
On the basis of the International Railways Union
(UIC) rules, the maximum acceptable value for SD
alignment is 1.4, while for SD vertical level is 2. In
this paper, three input and one output has been
chosen for the FIS; the output is the date of
intervention, while the input are ∆SD
alignment
,
∆SD
vertical
, ∆days, where:
– ∆SDalignment = 1.4 – measured SD alignment;
– ∆SDvertical = 2.1 – measured SD vertical
level;
– ∆days are the days past from the last tamping.
A set of 107 pairs of input- output vectors has been
used; in the table 1 a sample of the input database is
reported.
Table 1: Example of the input database
DATE SD
align.
SD
vert.
∆SD
align
∆SD
verti
∆days
15/1/92 1,23 1,78 0,17 0,32
27/1/92 TAMPING
15/2/92 0,88 1,06 0,52 1,04 18
15/3/92 0,87 1,08 0,53 1,02 48
15/4/92 0,89 1,08 0,51 1,02 78
15/5/92 0,89 1,12 0,51 0,98 108
15/7/92 0,91 1,12 0,49 0,98 168
15/8/92 0,89 1,16 0,51 0,94 198
15/9/92 0,89 1,14 0,51 0,96 228
.... .... .... .... .... ....
15/4/01 1,26 2,38 0,14 -0,28 1667
15/5/01 1,53 2,53 -0,13 -0,43 1697
15/7/01 1,52 2,5 -0,12 -0,4 1757
15/8/01 1,5 2,52 -0,1 -0,42 1787
15/9/01 1,54 2,59 -0,14 -0,49 1817
11/10/01 TAMPING
15/10/01 1 1,65 0,4 0,45 4
15/11/01 1,03 1,65 0,37 0,45 34
15/1/02 1,05 1,68 0,35 0,42 94
.. .. .. .. .. ..
15/5/02 1,09 1,78 0,31 0,32 214
15/7/02 1,11 1,84 0,29 0,26 274
This set of input vectors has been divided into two
groups:
– training vectors, used for training a neural
network, that will subsequently calibrate the
MF’s;
– checking vectors, used to check the model.
The MF’s used in our case are gaussian curves,
characterized by mean and standard deviation; the
output is a singleton.
The training results consist in calibrated MFs both
for input and output, as well as the rules of the
inference engine. In the following figures 4 and 5
the MF’s for ∆SD
alignment
and ∆SD
vertical
, respectively,
are reported. Of course, when both ∆SD
alignment
and
∆SD
vertical
are 0, the thresholds are reached; then, the
pair [0 0] as input allows to forecast when these
thresholds will be reached.
Note that not necessarily both thresholds will be
reached at the same moment. On the contrary, highly
likely this situation will never happen.
The proposed FIS uses the logical OR to get the
lowest value ∆SD as a precautionary condition. In
figure 6 are the rules of inference system obtained
by ANFIS.
4 ROBUSTNESS OF THE METHOD
TEST
A glaring mistake in measurement has been
simulated: one of the measured values has been put
over threshold, keeping hold other values. Table 2
shows the results of tests for different location of the
error; in particular, in the test 4 an error in the
second-last measure of SD of alignment has been
simulated. It is easy to see that the influence of a
measurement error on the FIS forecast is very low,
not greater than 8%. The reason is that the system
decision is based not only on a unique peak value,
but on an overall analysis of the trend, over time, of
the track parameters.
Table 2: Results of the tests
A DECISION SUPPORT SYSTEM BASED ON NEURO-FUZZY SYSTEM FOR RAILROAD MAINTENANCE
PLANNING
47
5 CONCLUSIONS
Main advantages in using such a kind of FIS are
flexibility, since thresholds are no longer crisp, and
versatility, since the forecast is carried out for each
specific track-segment and the method allows to take
into account the company policy as for maintenance.
Moreover, it is possible to use the expert knowledge,
without predefined mathematical models: in this
sense, the fuzzy inference is close to reasoning way
of railway officials and technicians.
Tamping 11 October 2001
The proposed model is also able to recognize glaring
mistakes in measurement, since it analyzes the
overall behavior of the track on the basis of the
whole body of training data. It also allows to
overcome some drawbacks of the binary logic. In
fact, without verifying the correctness of the
parameter value, according to binary logic approach
even if one value of the parameter exceed the
threshold then maintenance operations have to be
carried out.
Test
N
otes
date of
measure
SD align
SD vert.
days to
intervention
∆days %
1 reference 15-july-02 1,11 1,84 713 0
2 error on last measure 15-july-02 1,06 1,74 736 3.22
15-febr-02 1,02 2,11
3
error on fifth-last
measure
15-july-02 1,11 1,84
760 6.59
15-may-02 1,09 2,11
4
error on second-last
measure
15-july-02 1,06 1,84
765 7.29
5 error on last measure 15-july-02 1,11 2,11 718 0.70
An important difference between the two approaches
is relevant to the way of taking into account the two
considered parameters. In fact, Ecotrack considers
SD of alignment
and SD of longitudinal level
separately; then by linear extrapolation forecasts the
dates on which parameters threshold will
respectively be reached and assumes as tamping date
the closest one by applying a OR (logic) rule.
On the contrary, the FIS model consider both the
parameters at the same time: it is based on a
systemic and multicriteria approach to the
parameters values analysis. Thus, a parameters
correlation is implicitly assumed. Actually, in order
∆
SDalign=0
∆
SDvertical=0
forecast = 826
Figure 6: Rules of the fuzzy inference system
ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
48

to held higher safety level each fuzzy rule assumes
the lowest membership degree of the two parameter
by means of an AND (logic) rule.
For both the approaches a large amount of track
technical and geometrical qualitative and
quantitative data is needed and usually most of the
railways company do not have enough data.
Ecotrack assumes the available data within the
software database while the proposed FIS system the
data are used during the training phase of the ANN
and to validate the calibrated model.
Some problem to reach an effective and consistent
implementation of such a fuzzy system may occur
when there is a lack of data or when the analyst
assumes incorrect data as reliable. Actually, under
these assumptions rail track analysis is difficult
using traditional software too.
Further research will be devoted to improve the
proposed DSS. In particular, we will deal with:
– define a hierarchically higher analysis level in
order to gather homogeneous maintenance works
on adjacent track-segments; to this purpose we
are defining a Subtractive Clustering method;
– introducing new rules in order to allow the DSS
to carry out analysis when insufficient or
incorrect data are available;
– defining time-function of the track quality
indexes in order to determine a track
deterioration model closer to the theoretical one.
REFERENCES
Dell'Orco, M., Ottomanelli, M., Pace, P., Pascoschi, G.,
2002. Optimisation of Railway Maintenance Planning
Using Intelligent Decision Support Tools. In Proc. of
the 13
th
Mini-EURO Conf. on "Handling Uncertainty
in the Analysis of Traffic and Transportation Systems".
Polytechnic of Bari, 10-13, June 2002. pp. 218-223.
Bari, Italy
Esveld C., 2001. Modern Railway Track, MRT
Productions
Leung, M., Chuah, K.B., Rao Tummala, V.M., 1998. A
Knowledge–based System for Identifying Potential
Project Risks. Omega, n°5, 623 – 638
Jovanovic S., Esveld C., 2001. ECOTRACK: An objective
condition-based decision Support system for long-term
track M&R Planning directed towards reduction of
Life Cycle Costs. 7th International Heavy Haul
Conference, Brisbane, Australia
Zadeh, L.A.,1973. “Outline of a new Approach to the
Analysis of a complex Systems and Decision
Processes”. IEEE Transaction on Systems, Man and
Cybernetics, 3, pag. 28-44
Zimmermann, H. J., 1991. Fuzzy set theory and its
applications. Kluwer Academic Publisher, Dordrecht
Zoeteman, A., 2001. Maintaining the infrastructure of the
conventional railway network in the Netherlands,
State-of-the-art Report. May 2001
Miwa, M., Ishikawa, Oyama T., 2001. Modeling the
Transition Process of Railway Track Irregularity and
its Application to the Optimal Decision-Making for
Multiple Tie Tamper Operations. Railway Engineering
2000, London, July 2000
.
A DECISION SUPPORT SYSTEM BASED ON NEURO-FUZZY SYSTEM FOR RAILROAD MAINTENANCE
PLANNING
49
