
THE INDEX UPDATE PROBLEM FOR XML DATA IN XDBMS
Beda Christoph Hammerschmidt
1
, Martin Kempa
2
and Volker Linnemann
1
1
Institute of Information Systems
University of L
¨
ubeck
Ratzeburger Allee 160, D-23538 L
¨
ubeck, Germany
2
sd&m AG
software design & management
Carl-Wery-Str. 42, D-81739 M
¨
unchen, Germany
Keywords:
XML, Databases, Indexing, Updates.
Abstract:
Database Management Systems are a major component of almost every information system. In relational
Database Management Systems (RDBMS) indexes are well known and essential for the performant execution
of frequent queries. For XML Database Management Systems (XDBMS) no index standards are established
yet; although they are required not less. An inevitable side effect of any index is that modifications of the
indexed data have to be reflected by the index structure itself. This leads to two problems: first it has to be
determined whether a modifying operation affects an index or not. Second, if an index is affected, the index
has to be updated efficiently - best without rebuilding the whole index.
In recent years a lot of approaches were introduced for indexing XML data in an XDBMS. All approaches lack
more or less in the field of updates. In this paper we give an algorithm that is based on finite automaton theory
and determines whether an XPath based database operation affects an index that is defined universally upon
keys, qualifiers and a return value of an XPath expression. In addition, we give algorithms how we update our
KeyX indexes efficiently if they are affected by a modification. The Index Update Problem is relevant for all
applications that use a secondary XML data representation (e.g. indexes, caches, XML replication/synchro-
nization services) where updates must be identified and realized.
1 INTRODUCTION
The Extensible Markup Language (XML) has be-
come the standard data format for exchanging infor-
mation in information systems. XML is an easy and
flexible way to express semistructured data - inde-
pendent from platforms, programming languages and
operating systems. The increasing usage of XML
data demands the connection between XML tech-
nology and database management systems, because
the latter provide a fast, robust, and application in-
dependent way of storing and accessing data. In
recent years a multitude of native XML Database
Management Systems (XDBMS) were introduced by
commercial vendors (e.g. Tamino (Sch
¨
oning, 2001),
Xindice (Apache, )) and research projects (e.g. Natix
(Fiebig et al., 2002), InfonyteDB (Infonyte GmbH,
2003), Timber (Jagadish et al., 2002)). Like in re-
lational DBMS indexes are adopted to decrease the
execution time of frequent queries and may increase
the performance of an XDBMS up to factor 100,000
for realistic scenarios compared to a query execution
without any index. In contrast to relational DBMS,
where indexes and index structures are well known
since decades, indexes in XDBMS are still an active
field of research with no standards established yet. In
RDBMS only atomic values of specified columns are
reflected in an index; XML indexes have to cover both
the structure of the data and the values of elements.
A lot of approaches have been introduced in recent
years dealing with indexes for querying XML data.
The problem of updating an index is a minor focus
of most publications. If at all, the authors describe
how their data structure can be updated from a tech-
nical point of view. To the best of our knowledge,
the problem whether an XML index i is affected by a
modifying operation o is never faced before. We call
this problem the XML Index Update Problem (XIUP).
For expressing updates we have to select which
nodes (elements, attributes, or content) in the given
XML data have to be modified. XPath (World Wide
Web Consortium (W3C), ) is a selection language for
such a purpose. Due to space restriction we cannot
give an introduction to XPath. All examples in this
paper are given in the abbreviated syntax of XPath.
XPath itself cannot be used to modify the XML data.
27
Christoph Hammerschmidt B., Kempa M. and Linnemann V. (2005).
THE INDEX UPDATE PROBLEM FOR XML DATA IN XDBMS.
In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 27-34
DOI: 10.5220/0002524600270034
Copyright
c
SciTePress

Therefore a language like XUpdate (e.g. (XML:DB
XUpdate Working Group , )) is needed to express up-
date operations. XUpdate statements contain XPath
expressions to identify the nodes to be modified.
In this paper we assume that an index is selective;
i.e. it is defined to accelerate a specific query and
not all queries in general. Index approaches that are
not selective (e.g. Strong DataGuides (Goldman and
Widom, 1997)) reflect the whole XML data and may
lead to exhaustive space consumption. Additionally,
every modifying database operation affects the
non-selective index leading to an update. Therefore,
the Index Update Problem for non-selective indexes
is trivial. More about the characteristics of selective
and non-selective index approaches can be found in
previous works (B.C.Hammerschmidt et al., 2004a;
B.C.Hammerschmidt et al., 2004b). We motivate the
XIUP by two examples that operate on data from the
DBLP computer science bibliography project (Ley,
2001). The full DBLP data consists of approximately
500,000 publications, mainly articles, inproceedings
and books. The root node is called dblp and is the
parent node of the different publications.
Example: The index i
1
is defined to accelerate
XPath expressions of the shape of query q
1
:
q
1
= / dblp / book [ au thor = ’x ’ ]
Index i
1
indexes all book elements by the value of
their author child which is interpreted as a key for
this query. In our index approach KeyX all keys are
stored in a search tree offering logarithmic retrieval
time. Thus, if an authors name is given, we find the
corresponding books efficiently.
The XUpdate operation o
1
deletes all books that are
written by the author Kempa.
o
1
= <xupdate:remove
s e l e c t =/ dblp / book [ author = ’Kempa ’ ] >
</ xupdate:remove>
Obviously one can see that the index i
1
is affected by
o
1
because after executing o
1
there is no book author
’Kempa’ anymore in the data. The key ’Kempa’ has
to be removed from the index to keep it consistent.
At first glance, it seems easy to determine the
affection by comparing the contained XPath ex-
pressions which are equal in this example. But
because XPath expressions may contain more
complex navigational steps the decision can become
more difficult; this is shown in the following example.
Example: Index i
2
indexes all child elements
of the dblp element which have a title child that
is used as key.
q
2
= / dblp / ∗ [ t i t l e = ’x ’ ]
The modifying operation o
2
deletes all children of
all article elements.
o
2
= <xupdate:remove
s e l e c t =/ dblp / a r t i c l e / ∗ />
</ xupdate:remove>
First, one can remark that the contained XPath ex-
pressions are not equal. Second, without any schema
information like a DTD or XMLSchema we do not
know if the dblp element is allowed to have an
article element and that the article element
may have a child named title. Due to the wild-
card operator (*) it is not sufficient to perform a string
comparison of both XPath fragments. With one or
more descendant axis (//) this problem becomes even
more complex.
In this work we define the XML Index Update Prob-
lem (XIUP) formally and introduce an efficient algo-
rithm solving the XIUP for a fragment of XPath con-
taining node tests, the child axis (/), the descendant
axis (//), wildcards(*) and qualifiers ([]) without the
NOT operator. This class is called XP
{[],∗,//}
. The
algorithm calculates the intersection of two XPath ex-
pressions and checks its emptiness. For the more gen-
eral XPath fragment XP
{[],∗,//,NOT }
containing the
operator NOT in qualifiers the XIUP is still decidable
but becomes NP complete leading to inefficient al-
gorithms with exponential runtime in the worst case.
Further, we present algorithms for updating the key-
oriented XML index (KeyX).
The remainder of this paper is organized as follows:
In Section 2 we introduce and formalize an abstract
definition of an index structure for XML data. Sec-
tion 3 defines the XML Index Update Problem and re-
duces it to the Intersection Problem of XPath expres-
sions. Finite automata that calculate the emptiness of
the intersection are introduced in this section. In Sec-
tion 4 we present the implementation of updates in
KeyX. We survey related work in Section 5 and con-
clude the paper in Section 6.
2 INDEX AND UPDATE
DEFINITION
This paper focusses on selective indexes like the In-
dexFabrics (Cooper et al., 2001), APEX (Chung et al.,
2002) or our index approach called KeyX. Indexes
that are non-selective (e.g. Strong DataGuide (Gold-
man and Widom, 1997)) are indexing the whole XML
data. Therefore they are affected by every modifying
operation. This leads to a trivial XIUP. Non-selective
indexes perform best for read-only applications but
fail when changes occur frequently.
In order to define indexes we have to define XPath
based path expressions first. In this work we distin-
guish between simple and general path expressions.
Definition 1: Simple Path Expression:
A simple path expression p
s
for a given alphabet Σ
of element and attribute names is defined as follows:
p
s
::= p
s
/p
s
| p
s
//p
s
| ∗ | n | .
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
28

with / denoting the child axis, // the descendant axis,
∗ an arbitrary element and n a specific element with
the label n ∈ Σ; . is the current node. The set of all
simple path expressions is denoted by P
s
.
Based on the definition of simple path expressions
we define general path expressions which may
include key comparisons and qualifiers:
Definition 2: General Path Expression
A general path expression p for the XPath fragment
XP
{[],∗,//}
is defined as follows:
p ::= p/p | p//p | p[q]∗ | ∗ | n | .
q ::= p | p AND p | p OR p | n op v
r ::= = | < | > | <= | >=
v ::= string | int | float
where string, int, and float are string, integer and
float literals.
The path expressions of XP
{[],∗,//}
may have
structural qualifiers (sometimes called predicates)
and qualifiers with value comparisons. We call the
latter keys because the can be compared to keys in
relational indexes.
The grammar for the XPath fragment
XP
{[],∗,//,NOT }
has an additionally NOT oper-
ator in the rules for q.
The XIUP is relevant for any index approach.
We focus on our general KeyX definition. An
adoption to other index approaches can be made
easily because an index is defined universally upon
keys, qualifiers and one return value.
Example: For instance, the XPath query
q
3
= / dblp / ∗ [ author = ’Kempa ’ AND
year >2002][ is bn ]
selects all elements below dblp that match a given
author name and a range of year values. Addi-
tionally, the selected elements must have at least one
child named isbn. Because we have value compar-
isons for the author and year we call them keys.
The keys can be stored in an index’s data structure
optimized for fast key retrieval. Qualifiers may have
any value, only their existence is requested (here
isbn). Therefore, the value of qualifiers can be
ignored. The return value path is the path to the
elements that are selected by the XPath expression.
Definition 3: Index Declaration
Formally, a selective index i is defined as a triple
i = (K, Q, v) where K is a list of absolute simple
path expressions ∈ P
s
, referring to the key nodes.
Q a list of absolute simple path expressions ∈ P
s
,
referring to the qualifier nodes and v ∈ P
s
is a simple
path to the value nodes.
The path expressions to the keys, qualifiers and
the return value are extracted from a given XPath
expression using the extraction function described
in (B.C.Hammerschmidt et al., 2004a).
Example: The following index declaration de-
fines an index suited for the query q
3
:
i
3
= (
K = [ / dblp / ∗ / author , dblp / book / year ] ,
Q = [ / dblp / ∗ / isbn ] ,
v = dblp /∗
)
In general, a selective index covers all queries with
a result set being a subset of the path expression
that defines the index. For instance, the index i
3
may also be used to answer the following query
q
4
= /dblp/book[author=’Beda’][isbn]
because the result set of q
4
is a subset of q
3
. Details
about containment (subset) of XPath expressions can
be found in (Miklau and Suciu, 2004).
Because relevant keys can be found in logarithmic
time the linear process of comparing each element
that is referenced by the key path is avoided.
Because one selective index covers only a limited
number of queries we need a set of indexes to sup-
port a real application. The problem of finding a good
set of indexes for a given set of querying and modi-
fying database operations is part of the previous pub-
lication (B.C.Hammerschmidt et al., 2004b) dealing
with this so called Index Selection Problem. Queries
that are not covered by any index must be evaluated
conventionally by the XPath engine of the underlying
XDBMS.
Whenever a modifying operation adds or removes
an element or the content value of an element that is
referenced by at least one of the paths defining the in-
dex, an update of the index may be necessary to keep
index and original data consistent. For instance, if we
add a first isbn node to a book having already an
author and a year the index i
q
3
has to add this
new book because it is now in the result set of q
3
.
3 THE XML INDEX UPDATE
PROBLEM
In this section we introduce the XML Index Update
Problem (XIUP) and reduce it to the Intersection
Problem of two XPath expressions.
An index i covers a query q if the nodes returned
by the index structure are the same as the nodes re-
turned by the database itself. Because the index is
defined upon a return value and a set of keys and a
set of qualifiers, the index may be out-dated if one
of these nodes have changed. The key of an index
is a structural and a content property. Therefore we
have to update the index if a key appears, disappears
or its value changes. Qualifiers and the return values
THE INDEX UPDATE PROBLEM FOR XML DATA IN XDBMS
29

are only structural properties, the modification of their
values does not touch the index.
The index is affected by a modifying operation
if the path expressions defining the keys, qualifiers
or the return value selects at least one node that is
selected by the path expression of the modifying
operation. Formally, this means that the intersection
of the path expressions is not empty.
Definition 4: Affection
The affection of two XPath expressions p and p
′
∈
XP
{[],∗,//}
is defined as follows:
{ ∃ t ∈ T | p(t) ∩ p
′
(t) 6= ∅ }
with ∅ denoting the empty set. T denotes the set of all
XML data - any XML document that is well formed
is in T . p(t) with t ∈ T is the set of nodes of t
that is returned by the evaluation of p . We denote
Mod(p) ∈ T the set of all XML data where p returns
a non-empty result set.
Informally, the affection asks if there can be an
arbitrary XML document so that p and p
′
share at
least one node in their result sets. Actually, we are
not interested in that document but only if one may
exist or not. We determine the existence of such a
document by the use of finite automaton theory. A fi-
nite automaton is defined by its states and transitions.
See (Hopcroft et al., 2001) for details about finite
automaton theory. We give a procedure to create
finite automaton for simple path expressions before
we present the algorithm which checks affection.
Definition 5: Automaton for Mod(p)
We build an automaton A accepting Mod(p) as
follows:
A is a tuple (Q,Σ, σ, q
0
, F ) with Q = NODES(p)
a set of states, Σ a finite alphabet consisting of all
element names. σ is a function Q × Σ → Q
defining the set of transitions. q
0
is the initial state
whereas F is the set of final states. For each node
x ∈ NODES(p) with a child y, A has a transition
(y;
′
x
′
) → x with
′
x
′
∈ Σ the label of the node x. If
the label of x is a wildcard (*) then any symbol ∈ Σ
is valid for the transition. For every descendant edge
e from node x to node y, A has a transition (y;
′
∗
′
)
→ y. These transitions lead to a nondeterministic
automaton. The terminal state is ROOT(p).
Example: The simple XPath expression
q
5
= /a/ ∗ //c//d leads to an automaton A with
Q = {q
a
,q
∗
,q
b
,q
c
,q
0
} and σ = {t
0
... t
5
} with
t
0
= (q
0
;’d’) → q
d
,
t
1
= (q
d
;’*’) → q
d
,
t
2
= (q
d
;’c’) → q
c
,
t
3
= (q
c
;’*’) → q
c
,
t
4
= (q
c
;’*’) → q
∗
and finally
t
5
= (q
∗
;’a’) → q
a
.
The initial state is q
0
, q
a
is the one
final state. Please note that the tran-
sitions are not deterministic (e.g. t
3
,
t
4
). The automaton for this example
is illustrated in the Figure on the right
hands side.
q
a
a
*
c
d
*
*
q
*
q
c
q
d
Because we regard the intersection of simple path
expressions with all nodes having one child at maxi-
mum we can use standard finite automaton theory to
calculate the existence of an intersection. The more
complex tree automaton theory usually applied for
processing XML is not required. The following al-
gorithm checks the affection of two path expressions:
1. create automaton A accepting Mod(p);
2. create automaton A
′
accepting Mod(p
′
);
3. create product autom. B acc. Mod(p) ∩ Mod(p
′
);
4. < q
0
A
× q
0
A
′
> = initial state of B;
5. < q
F
A
× q
F
A
′
> = final state of B;
6. CLOS = transitive closure of < q
0
A
× q
0
A
′
>
7. if ( < q
F
A
× q
F
A
′
>∈ CLOS) return true;
else return false;
Figure 1: Pseudo code of the affection algorithm
In Step 1 the algorithm creates an automaton A ac-
cepting all XML data where p returns non-empty re-
sult sets . Analogue, Step 2 creates an automaton A
′
for path p
′
. In Step 3 the product automaton B of A
and A
′
is created. B accepts all XML data where both
path expressions p and p
′
evaluate to a non-empty re-
sult set. Informally, one can say that B simulates the
simultaneous execution of A and A
′
accepting if and
only if both automata are accepting.
If this is the case, at least one node of the XML data
is selected by both p and p
′
and the index defined over
p is affected by p
′
and must therefore be updated.
In the last steps of the algorithm it is checked if there
is a path from the initial state to a final state of B by
calculating the transitive closure of the initial state of
B. Please note that the emptiness of the intersection is
a property of the product automaton. It is determined
without processing any concrete XML input
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
30

Algorithm: Update a KeyX index for an Insert operation
Input: 1. KeyX index with declaration x = (K
p
, Q
p
, v
p
)
2. Insert operation with node i
n
and path i
p
Output: The KeyX index x is updated concerning i
n
.
Method: 1. if isAffected(k
i
p
− i
p
, i
′
p
) with i
′
p
∈ path(i
n
) and k
i
p
∈ K
p
then
/* the Insert operation may contain an indexed key value */
repairKeys(x, i
n
, i
p
)
2. if isAf fected(q
i
p
− i
p
, i
′
p
) with i
′
p
∈ path(i
n
) and q
i
p
∈ Q
p
then
/* the Insert operation may contain a qualifier */
repairQualif ier(x, i
n
, i
p
)
3. if isAf fected(v
p
− i
p
, i
′
p
) with i
′
p
∈ path(i
n
) then
/* the Insert operation may contain an indexed return value */
repairV alues(x, i
n
, i
p
)
Figure 2: Update algorithm of KeyX for an Insert operation
Algorithm: Repair Keys after Insert operation
Pre: Insert operation may contain new indexed key value
Input: 1. KeyX index with declaration x = (K
p
, Q
p
, v
p
)
2. Insert operation with node i
n
and path i
p
Output: The keys of KeyX index x are updated concerning i
n
.
Method: Foreach father node f
n
∈ root(db).query(i
p
) to be inserted in do
1. Foreach key value node k
i
n
∈ i
n
.query(k
i
p
− f
p
) do // k
i
n
is a new partial key
(a) Foreach key value node K
n
∈ k
i
n
.query(K
p
− k
i
p
) do // K
n
is the key of k
i
n
i. add return value node to index with x.add(K
c
, r
n
) and r
n
∈ K
n
.query(v
p
− K
p
)
if r
n
∈ x.returnV alues(K
n
)
Figure 3: Repair algorithm for keys after an Insert operation
4 UPDATE ALGORITHM FOR
KeyX
This section introduces the update algorithm for the
KeyX data structure for the insert operation. The
algorithms for the replace and delete operations are
omitted here for space reasons and are defined analo-
gously. Every replace operation can be expressed by
a delete operation followed by an insert operation.
The section is finished by presenting performance
measurements of our implementation for the KeyX
index system.
Algorithms updating the index structure
The algorithms presented in this section make use
of some further methods and operations introduced
first. The operation
′
−
′
from the path interface can
be applied to two simple paths p
1
− p
2
. It returns the
path from a node with path p
2
to a node with path p
1
.
The operation is extended for a tuple of paths as first
or second parameter. In this case it returns a tuple of
difference paths. The method path applied to a node
n returns a list of the paths to all sub-nodes of n.
Additionally a method is needed to navigate to a path
expression from a given context node. This is realized
by method query. With n.query(p) the path p is
evaluated concerning the context node n. The result
of this method is a list of nodes. Further, the method
add and returnV alues from the interface of the
KeyX implementation are used. With x.add(K
c
, r
n
)
a return node r
n
can be added to the key value entry
K
c
in index x. The method x.returnV alues(K
n
)
returns the return values of the key nodes K
n
taking
the qualifiers of the index declaration into account.
Generally all identifier with subscript p represents the
path of a node, with subscript n the node itself and
with subscript c the content of the node.
Now the update algorithm for an KeyX index
concerning an insert operation can be presented in
Figure 2.
In a first step the algorithm determines if a node
is inserted which relate to an indexed key value, in-
dexed qualifier node, or to an indexed return value
node. If one of these cases is true the belonging key
value nodes are extracted from the database and in-
serted with the relevant return value nodes into the
index.
THE INDEX UPDATE PROBLEM FOR XML DATA IN XDBMS
31
Algorithm: Repair Values after Insert operation
Pre: Insert operation may contain new values
Input: 1. KeyX index with declaration x = (K
p
, Q
p
, v
p
)
2. Insert operation with node i
n
and path i
p
Output: KeyX index x is updated for new values concerning i
n
.
Method: Foreach father node f
n
∈ root(db).query(i
p
) to be inserted in do
1. Foreach return value node r
n
∈ i
n
.query(v
p
− f
p
) do // r
n
is a possible new return value
(a) Foreach key value node K
n
∈ r
n
.query(K
p
− v
p
) do // K
n
is the key of r
n
i. add return value node to index with x.add(K
c
, r
n
) if r
n
∈ x.returnV alues(K
n
)
Figure 4: Repair algorithm for values after an Insert operation
The algorithm is sound and complete for the XPath
fragment XP
{[],∗,//}
because excluding qualifiers
cannot be expressed in this class.
The more general class XP
{[],∗,//,NOT }
allows to
express qualifiers in p and p
′
that cannot be fulfilled
simultaneously. For instance, if p = /a[b] and
p
′
= /a[N OT (b)] it is obvious that there can be no
element a having a child b and no child b at the same
time. In this case, the algorithm is still complete
but not sound meaning that an index affection is
indicated where it is not the case. A redundant index
update is effected.
A sound and complete algorithm in general cannot be
as efficient because the XIUP for the XPath fragment
XP
{[],∗,//,NOT }
is NP hard (the NP-complete
problem 3SAT can easily be reduced to the XIUP
by attaching child nodes representing the clauses
from 3SAT to one root node). The proof of the
NP-completeness of the XIUP is beyond the scope of
this paper.
Measurements:
In order to judge our approach we measured the
performance of the algorithm in Figure 2. KeyX
and the algorithms of this paper are done in Java.
We performed all tests on a Pentium 4 with 2.66
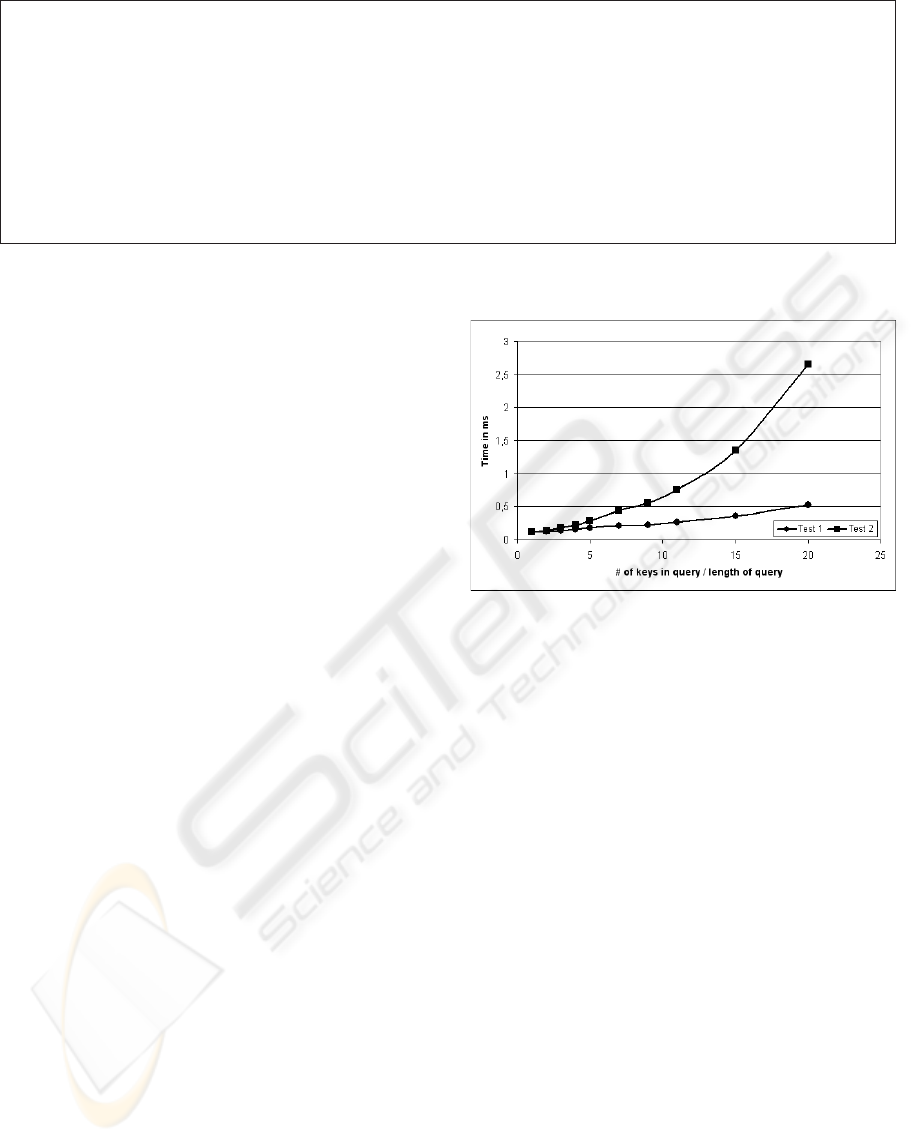
Ghz and 1 Gb main memory. In Test 1 we increased
the number of keys in the index’s definition. As
the diagram in Figure 5 shows the execution time
increases linearly. When increasing the number of
keys and the length of the path expressions defining
the index the execution time increases quadratically;
this is shown in the second graph.
Even for very complex indexes with more than 20
keys and path expressions of the length about 20 the
XIUP can be solved in less than 3 milliseconds. When
an index is affected the underlying index structure has
to be updated by inserting/removing a key or updating
the reference of the return value. Compared to a total
rebuild of an index which may take minutes for tra-
versing the whole XML data this approach is a major
improvement. For applications that frequently update
Figure 5: Measurements of the Index Affection algorithm
an XML database (e.g. orders in an online shop) the
approach offers a suitable index system.
5 RELATED WORK IN
INDEXING XML
In recent years a multitude of approaches for indexing
XML were introduced. One common approach to
index the structure of semistructured data are the so
called structural summaries. One early approach are
the Strong DataGuides (Goldman and Widom, 1997)
providing a general index structure to accelerate
path expressions starting at the root. References to
elements that are reached by the same path expression
are summarized in one node of the DataGuide. The
creation of a DataGuide can be compared to the trans-
formation of a nondeterministic finite state machine
to a deterministic one by the fusion of equivalent
states. DataGuides differ significantly from indexes
in RDBMS: Instead of accelerating specific queries
very efficiently they try to improve the evaluation of
path expressions in general. In contrast to indexes in
RDBMS where indexes are selected by the database
administrator, structural summaries in XDBMS are
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
32

permanently enabled and thus not selective.
The idea of the DataGuide is extended in sev-
eral works. The problem of non-selective and large
DataGuides is faced in the work of Kaushik et
al (Kaushik et al., 2002) introducing a selective
structural summary.
The same problem motivates the Adaptive Path Index
(APEX) (Chung et al., 2002) from Chung et al. APEX
is a specific structural index optimized for frequent
queries ignoring the values of elements. Therefore, it
is less efficient for queries containing a key.
Structural summaries are the main data structure or
part of further works, including the Forward-and-
Backward-Index (Abiteboul et al., 1999) the T-Index
(Milo and Suciu, 1999) (with the special cases
1-Index and 2-Index), the D(K)-Index (Chen et al.,
2003), HOPI (Schenkel et al., 2004) and others (Barg
and Wong, 2003; Halverson et al., 2003; Kaushik
et al., 2004; Weigel et al., 2003). Although some
of the work discuss how to update the index’s data
structure none of them explain how an affection is
determined.
Numbering schemes (e.g. (Grust, 2002; H. Jiang and
H. Lu and W. Wang and B. Ooi, 2003)) map each
element of the XML data to one or more numbers that
are mostly determined by post/preorder XML-tree
traversing algorithms. The numbers are used for a
faster retrieval of relationships between elements. For
some numbering schemes a change in the structure
means a recalculation of each assigned number -
this can cost as much as rebuilding the total index.
This problem is faced in the work (Kha et al., 2001)
proposing a numbering schema that is optimized for
updates leading to less number recalculation when
the XML data is modified. Again, none of these
paper faces the XIUP.
The Index Fabric (Cooper et al., 2001) is a bal-
anced tree structure storing the encoded paths from
the root to each node and its values. Therefore, the
Index Fabric support queries with keys and qualifiers.
The data structure of the Index Fabric - a Patricia
trie - can be updated easily like any other search
tree. But the question whether an index is affected
by a modifying operation is not mentioned by the
authors. Our index approach KeyX can be compared
with the index Fabric. Compared to the Index Fabric
KeyX supports more query types including multi-key
queries and range queries.
Approaches that uses an underlying relational
DBMS to store and index XML (e.g. (Bauer et al.,
2003)) have in common that they can reuse existing
and performant implementations of the relational
world. However, XML queries have to be mapped
to SQL queries leading to many expensive Join
operations if a multi-key query is executed. This
lead to performance degradation compared to native
XDBMS.
Recapitulating, a lot of XML index approaches
where introduced in the past. Early approaches
even have underlying data structures that cannot be
updated efficiently. Recent approaches use updatable
data structures but - to the best of our knowledge -
we are the first that present an algorithm that detects
if an existing index must be updated in order to keep
it consistent.
6 CONCLUSION
In this paper we defined the XML Index Update Prob-
lem (XIUP) and proposed an efficient algorithm solv-
ing the XIUP for the XPath fragments of the class
XP
{[],∗,//}
. We showed that the XIUP for more gen-
eral XPath expressions is NP complete but the algo-
rithm is still identifies all required index updates. The
XIUP is relevant for all approaches that try to index
XML data. To the best of our knowledge we are the
first who pay attention to the XIUP and introduced an
efficient algorithm.
Future work will deal with efficient algorithms
finding a (sub-)optimal sound-and-complete ap-
proximation for XPath fragments of the class
XP
{[],∗,//,NOT }
. A major constraint is that any ap-
proximation has to be completed in order to identify
required index updates and to keep the index and the
data consistent.
ACKNOWLEDGMENTS
We would like to thank Konstantin Ens for imple-
menting the intersection automata and the update al-
gorithms for our KeyX index structure in the scope of
his student research project.
REFERENCES
Abiteboul, S., Suciu, D., and Buneman, P. (1999). Data on
the Web: From Relations to Semistructured Data and
XML. Morgan Kaufmann, USA, 1st edition edition.
Apache. Xindice. URL: http://xml.apache.org/
xindice/.
Barg, M. and Wong, R. (2003). A fast and versatile path
index for querying semistructured data. In Proceed-
ings of the 8th International Conference on Database
THE INDEX UPDATE PROBLEM FOR XML DATA IN XDBMS
33

Systems for Advanced Applications (DASFAA 2003),
Kyoto, Japan.
Bauer, M. G., Ramsak, F., and Bayer, R. (2003). Multidi-
mensional mapping and indexing of xml. In Proceed-
ings of the 10th BTW Conference: Datenbanksysteme
f
¨
ur Business, Technologie und Web, volume 26 of LNI,
pages 305–323, Leipzig, Germany. GI.
B.C.Hammerschmidt, Kempa, M., and Linnemann, V.
(2004a). On the index selection problem applied to
key oriented xml indexes. Technical report, A-04-
09, Institute of Information Systems, University of
L
¨
ubeck.
B.C.Hammerschmidt, Kempa, M., and Linnemann, V.
(2004b). A selective key-oriented xml index for the in-
dex selection problem in xdbms. In Proceedigns of the
15th International Conference on Database and Ex-
pert Systems Applications - DEXA ’04, volume 3180
of Lecture Notes in Computer Science, pages 273–
284, Zaragoza, Spain.
Chen, Q., Lim, A., and Ong, K. W. (2003). D(k)-index:
an adaptive structural summary for graph-structured
data. In Proceedings of the 2003 ACM SIGMOD con-
ference, San Diego, California, USA, pages 134 – 144,
San Diego, California, USA.
Chung, C., Min, J., and Shim, K. (2002). Apex: an adap-
tive path index for xml data. In Proceedings of the
2002 ACM SIGMOD Conference, Madison, Wiscon-
sin, USA, pages 121–132. ACM Press.
Cooper, B. F., Sample, N., Franklin, M. J., Hjaltason, G. R.,
and Shadmon, M. (2001). A fast index for semistruc-
tured data. In Proceedings of 27th International Con-
ference on Very Large Data Bases, Roma, Italy. Mor-
gan Kaufmann.
Fiebig, T., Helmer, S., Kanne, C.-C., Moerkotte, G., Neu-
mann, J., Schiele, R., and Westmann, T. (2002).
Anatomy of a native xml base management system.
VLDB Journal, 11(4).
Goldman, R. and Widom, J. (1997). Dataguides: Enabling
query formulation and optimization in semistructured
databases. In VLDB’97, Proceedings of 23rd Interna-
tional Conference on Very Large Data Bases, pages
436–445. Morgan Kaufmann.
Grust, T. (2002). Accelerating xpath location steps. In
Proceedings of the 2002 ACM SIGMOD Conference,
Madison, Wisconsin, USA, pages 109–120.
H. Jiang and H. Lu and W. Wang and B. Ooi (2003). XR-
Tree: Indexing XML Data for Efficient Structural
Join. In Proceedings of the 19th International Con-
ference on Data Engineering (ICDE), pages 253–263,
Bangalore, India.
Halverson, A., Burger, J., Galanis, L., Kini, A., Krishna-
murthy, R., Rao, A. N., Tian, F., Viglas, S. D., Wang,
Y., Naughton, J. F., and DeWitt, D. J. (2003). Mixed
mode xml query processing. In VLDB’03, Proceed-
ings of 29rd International Conference on Very Large
Data Bases, pages 225–236, Berlin, Germany.
Hopcroft, J. E., Motwani, R., and Ullman, J. D. (2001). In-
troduction to Automata Theory, Languages, and Com-
putation. Addison Wesley Publishing Company.
Infonyte GmbH (2003). Infonyte DB. URL: http://
www.infonyte.com.
Jagadish, H., Al-Khalifa, S., Lakshmanan, L., Nierman, A.,
Paparizos, S., Patel, J., Srivastava, D., and Wu, Y.
(2002). Timber: A native xml database. Technical
report, University of Michigan, USA.
Kaushik, R., Bohannon, P., Naughton, J. F., and Korth,
H. F. (2002). Covering indexes for branching path
queries. In Proceedings of the ACM SIGMOD con-
ference, Madison, Wisconsin, USA.
Kaushik, R., Krishnamurthy, R., Naughton, J. F., and Ra-
makrishnan, R. (2004). On the integration of structure
indexes and inverted lists. In Proceedings of the ACM
SIGMOD conference, Paris, France, pages 779 – 790.
ACM Press.
Kha, D. D., Yoshikawa, M., and Uemura, S. (2001). An
XML indexing structure with relative region coordi-
nate. In 2001, I. C. S., editor, Proceedings of the 17th
International Conference on Data Engineering (ICDE
2001), pages 313–320, Heidelberg, Germany.
Ley, M. (2001). Digital Bibliography & Library Project.
URL: http://dblp.uni-trier.de. Computer
Science Bibliography.
Miklau, G. and Suciu, D. (2004). Containment and equiva-
lence for a fragment of xpath. J. ACM, 51(1):2–45.
Milo, T. and Suciu, D. (1999). Index structures for path ex-
pressions. In Proceedings of Database Theory - ICDT
’99, 7th International Conference, volume 1540 of
Lecture Notes in Computer Science, pages 277–295,
Jerusalem, Israel. Springer.
Schenkel, R., Theobald, A., and Weikum, G. (2004). Hopi:
An efficient connection index for complex xml docu-
ment collections. In Proceedings of the 9th Interna-
tional Conference on Extending Database Technology
(EDBT), volume 2992 of Lecture Notes in Computer
Science, pages 237–255.
Sch
¨
oning, H. (2001). Tamino - a dbms designed for xml. In
Proceedings of the 17th International Conference on
Data Engineering, pages 149–154, Heidelberg, Ger-
many. IEEE Computer Society.
Weigel, F., Meuss, H., Bry, F., and Schulz, K. U. (2003).
Content-Aware DataGuides for Indexing Large Col-
lections of XML Documents. Technical Report PMS-
FB-2003-14, Institute of Informatics, University of
Munich.
World Wide Web Consortium (W3C). XML Path Lan-
guage (XPath). URL: http://www.w3.org/TR/
xpath.
XML:DB XUpdate Working Group . XUpdate - XML
Update Language. URL: http://xmldb-org.
sourceforge.net/xupdate.
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
34
