ANALYTICAL AND EXPERIMENTAL EVALUATION OF
STREAM-BASED JOIN
Henry Kostowski
Department of Computer Science, University of Massachusetts - Lowell
Lowell, MA 01854
Kajal T. Claypool
Department of Computer Science, University of Massachusetts - Lowell
Lowell, MA 01854
Keywords:
Data Streams, Continuous Queries, Join, Main Memory Joins.
Abstract:
Continuous queries over data streams have gained popularity as the breadth of possible applications, ranging
from network monitoring to online pattern discovery, have increased. Joining of streams is a fundamental issue
that must be resolved to enable complex queries over multiple streams. However, as streams can represent
potentially infinite data, it is infeasible to have full join evaluations as is the case with traditional databases.
Joins in a stream environment are thus evaluated not over entire streams, but on specific windows defined on
the streams. In this paper, we present windowed implementations of the traditional nested loops and hash join
algorithms. In our work we analytically and experimentally evaluate the performance of these algorithms for
different parameters. We find that, in general, a hash join provides better performance. We also investigate
invalidation strategies to remove stale data from the window buffers, and propose an optimal strategy that
balances processing time versus buffer size.
1 INTRODUCTION
The proliferation of the Internet, the Web, and sensor
networks have fueled the development of applications
that treat data as a continuous stream, rather than as
a fixed set. Telephone call records, stock and sports
tickers, streaming data from medical instruments, and
data feeds from sensors are examples of streaming
data. As opposed to the traditional database view
where data is fixed (passive) and the queries consid-
ered to be active, in these applications data is consid-
ered to be the active component, and the queries are
long-standing or continuous. Recently, a number of
systems have been proposed (Babu and Widom, 2001;
Motwani et al., 2003; Babcock et al., 2002; Carney
et al., 2002; Chen et al., 2000) to address this para-
digm shift from traditional database systems to now
meet the needs of query processing over streaming
data.
Many of the proposed data stream management
systems (DSMSs)(Babu and Widom, 2001; Motwani
et al., 2003; Babcock et al., 2002; Chen et al., 2000)
are based on relational databases, with suitable mod-
ifications to handle streaming data. Typically in a
DSMS, the streaming data is given by tuples that fol-
low a fixed schema. Given this perspective, a stream
is similar to an infinitely extended relational table in
the sense that the table is never closed and can al-
ways be extended in the future. Queries against such
streams are composed of stream operators that at-
tempt to preserve as much as possible the semantics of
the familiar relational operators. However, the poten-
tially infinite nature of data streams poses difficulties
in both the definition of the semantics of such stream
operators as well as their implementation. One of the
key challenges is therefore to provide stream opera-
tors with well-defined semantics that nevertheless do
not require infinite storage and resources to compute
their results.
There are two basic approaches for providing se-
mantics for stream operators. The first approach is
to compute summary information. A data stream
is queried to produce a statistical summary of the
data seen so far. New data increments the statisti-
cal summary and can then be thrown away. The sec-
ond approach is to compute exact results while at the
same time limiting the memory resources required for
the computation. This approach adds a time win-
dow to the definition of query operators so that only
data falling within the time window produces results.
When data falls outside the window it can be dis-
carded since by definition it cannot produce any new
154
Kostowski H. and T. Claypool K. (2005).
ANALYTICAL AND EXPERIMENTAL EVALUATION OF STREAM-BASED JOIN.
In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 154-161
DOI: 10.5220/0002526701540161
Copyright
c
 SciTePress

results. However, to efficiently answer a query and to
provide scalability of user queries a query optimizer
must be able to analyze and compare the cost of the
different implementations of these windowed stream
operators. Towards that end, in this paper we provide
an analytical and experimental comparison of two im-
plementations of a windowed join operator.
The windowed join operator computes the join be-
tween two streams A and B, with windows windowA
and windowB respectively, using timestamps to limit
the possible matches. A tuple from stream A,
t
A
, with timestamp time(t
A
), may join with an
earlier tuple from stream B, t
B
, with timestamp
time(t
B
), only if time(t
A
) − time(t
B
) <
windowB. The symmetric statement holds with t
A
and t
B
interchanged. Based on this definition, the
window join is well-defined provided the tuples are
processed in order of their timestamps. If a tuple’s
timestamp is given by time-of-arrival at the join input
then the total order requirement is fulfilled.
In this paper we examine the performance char-
acteristics of two implementations, namely the win-
dowed nested-loops and the windowed hash, of a win-
dowed join operator. We use an evaluation metric
based on a rate-based cost model that can be used
by the query optimizer to determine the best plan
for evaluating a query over streaming data(Viglas and
Naughton, 2002). The cost model incorporates the
costs for the three fundamental steps that compose
each algorithm, namely scan, invalidation and inser-
tion. For a tuple t
A
arriving on stream A, scan is the
cost of scanning the stream B buffer for a match. In-
sertion is the cost of inserting the tuple t
A
into stream
A’s window buffer, and invalidation is the cost of re-
moving the expired tuples from the window buffers.
A tuple is considered to be expired if it’s time-stamp
falls outside the defined window for its stream. For
each step we posit an average time per tuple cost and
combine this cost with the rates of the inputs to derive
a formula for the total processing cost. In this paper,
we derive the cost formulas for each of the algorithms
and compare them to the experimental measurements.
However, the cost model considers only the time
cost of the join algorithms, and not the memory re-
sources utilized by each of the algorithms. For scala-
bility of stream operators, where resource contention
can be a primary issue, such an analysis is essential.
In our work we consider four invalidation strategies,
namely invalidation of tuples at scan time, invalida-
tion of all buffers at once, and the invalidation of only
the buffers that are actually probed. For each of these
invalidation strategies we present an analytical model
to evaluate both their processing cost as well their
effect on memory utilization. We show experimen-
tally that the best choice is likely to be to invalidate a
bucket only when it is probed or scanned. The invali-
dation requirement of the join operators as discussed
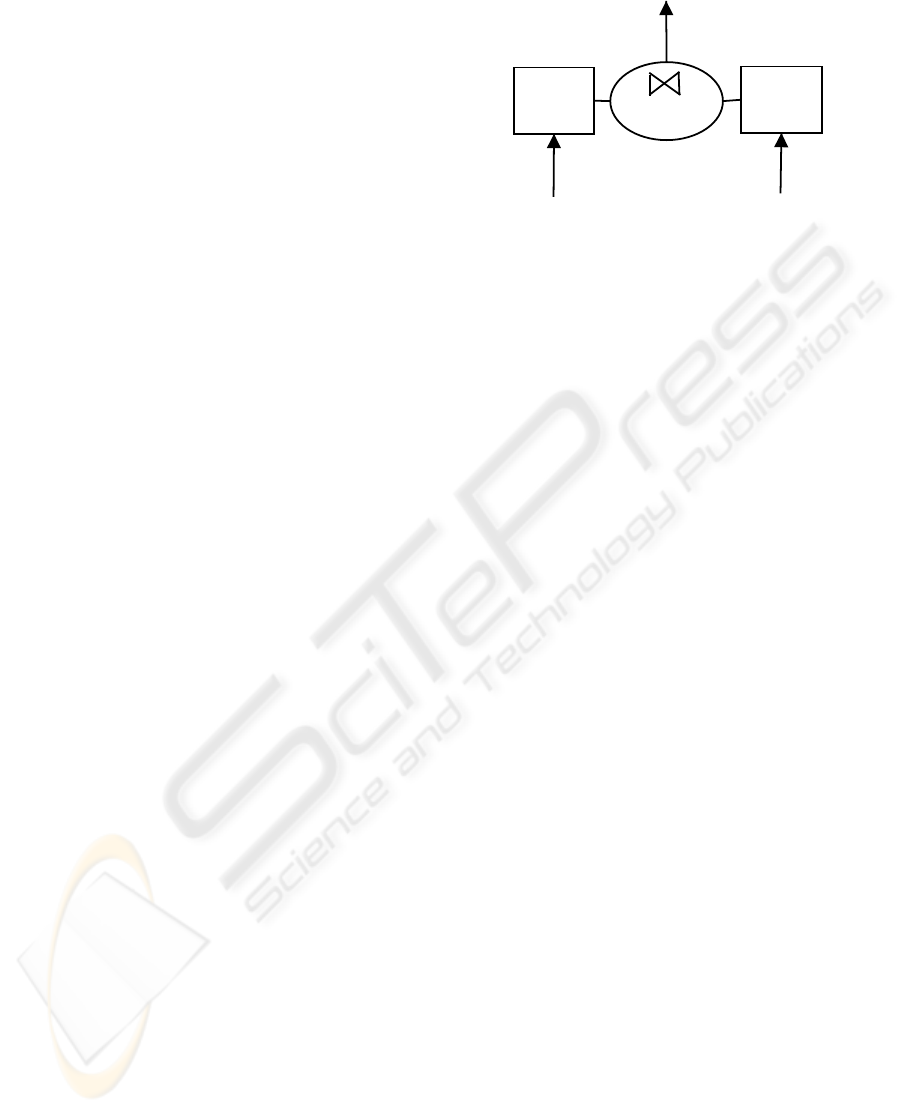
Window
Buffer
A
Window
Buffer
B
Window Join
Operator
Input
Stream B
Input
Stream A
Output
Stream
Figure 1: The Window Join Operator.
here can be easily extended to other windowed stream
operators.
Roadmap. The rest of the paper is organized as
follows. Section 2 presents an overview of the two
windowed join algorithms. In Sections 3 and 4 we
present our analysis and experimental results. We
conclude in Section 6.
2 WINDOWED JOIN
ALGORITHMS
In this section, we present windowed versions of two
widely used join algorithms, namely the nested loops
and the hash join algorithms(Ullman and Widom,
1997). In the windowed version, timestamps are as-
signed to tuples as they arrive for processing on either
of the windowed join’s two inputs. Both windowed
algorithms, WNL (windowed nested loops) and WHJ
(windowed hash join), share a common structure as
shown in Figure 1. Here, there are two input streams.
Each input stream has a buffer that holds (at least)
one window’s worth of tuples. We term the stream
on which a tuple arrives the arrival stream, and we
call the other stream the opposite stream. Whenever
a tuple arrives on one stream, the opposite stream’s
window buffer is probed to check for matching join
attributes. The tuple is then placed in the arrival
stream’s window buffer. Invalidation of stale tuples
in a window buffer can be performed at probe time,
when a tuple arrives on the opposite stream, or at
insertion time, when a tuple arrives on the arrival
stream.
Windowed Nested Loops Join. In the WNL algo-
rithm, the window buffer of each stream is given by a
circular buffer structure ordered by arrival time stamp.
When a tuple t
A
arrives on one of the streams, say
stream A, the tuples in the opposite stream’s (stream
B’s) window buffer (B) are first checked for expired
ANALYTICAL AND EXPERIMENTAL EVALUATION OF STREAM-BASED JOIN
155

tuples. The remaining tuples in the window buffer B
are then scanned to match, based on the join attribute,
with the arriving tuple. The newly arrived tuple t
A
is inserted at the head of arrival stream’s (stream A)
window buffer (A). Lastly, theexpired tuples at the tail
of the window buffer A are removed. This last step is
optional from the point of view of the semantics of
the window join. That is, failure to remove these ex-
pired tuples will not produce erroneous results since
they will also be expired when a new tuple arrives to
be processed on the opposite stream (stream B). Note
that this property is solely due to the assumed correct
arrival ordering property of tuple timestamps. How-
ever, failure to expire these tuples will cost in memory
resources, which could be significant depending on
the relative arrival rates of the two streams. Figure 2
outlines the windowed nested loops join algorithm.
WNL (Stream A, Stream B) {
event: (tuple arrives on stream A) do {
while (bottom tuple in buffer B expired) do
remove bottom tuple from buffer B;
for each (tuple in buffer B) do
if match then form join tuple and output;
insert (tuple) on head of buffer A;
//next step is optional
while (tail tuple in buffer A expired)
remove tail tuple from buffer A;
}
}
Figure 2: Windowed Nested Join Algorithm.
Windowed Hash Join. For the Windowed Hash
join, the window buffer of each stream is divided into
hash buckets based on the join attributes. When a tu-
ple t
A
arrives on stream A, it is hashed to the corre-
sponding bucket of the opposite stream’s (stream B)
window buffer. Expired tuples in this bucket are re-
moved, and the bucket is then scanned for matches.
The arriving tuple t
A
is hashed into the correct hash
bucket of the arrival stream’s window buffer A and
(again optionally) the bucket is scanned for expired
tuples. The hash buckets are individually arranged
as circular buffers in order of time stamp to facili-
tate checking for expired tuples. Figure 3 outlines the
windowed hash join algorithm.
Invalidation Strategies. Both join algorithms dis-
cussed in this paper must remove expired tuples from
the buffer about to be scanned before the scan phase
to ensure that the presence of stale tuples does not
produce erroneous results. This is the first remove
step in the algorithms given in Figures 2 and 3. In
WHJ (Stream A, Stream B) {
event: (tuple arrives on stream A) do {
compute hash(tuple.joinAttributes)
retrieve handle to corres. hashbucket B;
//next steps use the circular buffer structure of
// each hash bucket
while (tail tuple in hash bucket B expired) do
remove tail tuple from hash bucket B;
for each (tuple in hashbucket B) do
if match then form join tuple and output;
retrieve handle to corres. hashbucket A
insert (tuple ) into hashbucket A
//next step is optional
while (tail tuple in hashbucket A expired)
remove tail tuple from hashbucket A;
}
}
Figure 3: Windowed Hash Join Algorithm.
addition to this required remove step, additional re-
move steps may be employed to delete expired tuples
as soon as possible in order to decrease buffer sizes.
For example, in the case of the windowed hash join
(nested loops can be considered a windowed hash join
with only one hash bucket), we can check and remove
expired tuples in the insertion buffer prior to the in-
sertion phase. This is indicated by the second remove
step in the algorithms given in Figure 2 and 3. Addi-
tionally, each remove step in the windowed hash join
algorithm may also scan all other buckets to remove
stale data before it can accumulate. Based on our im-
plementation using circular buffers, stale tuples can
only exist at the bottom of the circular buffer. Thus,
the cost of invalidation of a hash bucket is the product
of the tuple invalidation cost and the number of stale
tuples in the buffer. The added cost of scanning all
the buckets is the cost of scanning at least the bottom
tuple in each bucket.
3 ANALYTIC COST MODEL
In this section we present a cost model, based on the
average cost metric introduced by Viglas et al.(Viglas
and Naughton, 2002), to evaluate the total process-
ing costs of the two join algorithms described in Sec-
tion 2. While Viglas et al.(Viglas and Naughton,
2002) focus on the output rate of a stream operator, an
important quantity for a query optimizer to calculate
in order to guarantee a certain result rate, we focus on
the scalability of the operators. Towards that end we
analyze the average cost per unit time of the join op-
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
156

erator. We also look at the effect of the invalidation
strategies on the use of memory resources.
3.1 Total Processing Cost
In general, the average cost per unit time of the join
operator is given by the average cost of processing
one tuple on one input multiplied by the input rate.
For each operator the half-cost, that is, the theoreti-
cal cost to process one of the input streams, is com-
puted first. Then the total cost, the cost to process
both input streams, given by the sum of the two half-
costs is calculated. We assume that the operators are
symmetric in their inputs to simplify the cost formu-
las. For the windowed nested loops join this total cost
Cost(WNL)
total
, is given as:
C(W NL)
total
= 2 ∗ Cost(W NL)
half
where Cost(WNL)
half
= λ
A
(C
t
). Here, λ
A
is the
rate of arrival of the tuples on stream A; and C
t
is the
cost to handle one tuple and is given as:
C
t
=
λ
B
λ
A
C
inv alidate
+ T
B
λ
B
C
scan
+ C
insert
Here λ
B
is the rate of arrival of tuples on stream B,
C
inv alidate
is the cost of invalidating tuples in the win-
dow buffer B of the stream B. Recall that invalidation
is the garbage collection of the expired tuples from the
buffers of the input streams. A tuple is considered to
be expired if it’s time-stamp falls outside the defined
window for its stream. The term T
B
is the size in sec-
onds of the window on the stream B input, C
scan
the
cost of scanning the tuples in the window buffer B for
a match, and C
insert
is the cost of inserting a tuple into
the window buffer A of the stream A. The factor
λ
B
λ
A
gives the average number of buffer tuples that need
to be invalidated upon arrival of a tuple on stream A.
Thus, under the symmetry assumption (in particular
that the insertion, invalidation, and scan costs are the
same on both inputs), the total cost of computing a
join for tuples arriving on the two streams A and B is
as given in Equation 1.
C(W NL)
total
= (λ
A
+ λ
B
)(C
inv alidate
+ C
insert
)
+λ
A
λ
B
(T
A
+ T
B
)C
scan
(1)
Similarly, the total cost of evaluating the join of two
streams A and B using a windowed hash join algo-
rithm is given as the sum of its two half-costs. For
a windowed hash join, the half cost, C(W HJ)
half
is
given as:
C(W HJ)
half
= λ
A
(
λ
B
λ
A
C
inv alidate
+
T
B
λ
B
N
B
C
scan
+ C
insert
)
where N
B
is the number of hash buckets on stream
B’s side. The total cost for a windowed hash join is
given as:
C(W HJ)
total
= (λ
A
+ λ
B
)(C
inv alidate
+ C
insert
)
+
λ
A
λ
B
N
B
(T
A
+ T
B
)C
scan
(2)
Equation 1 and 2 show that both the algorithms,
windowed nested loops (WNL) and the windowed
hash join (WHJ), have the same overall functional de-
pendence on the input rates. In particular, holding
one of the input rates fixed, the average cost per unit
time depends linearly on the input rate of the second
stream. This similarity is not unexpected when we
consider that the hash join algorithm with only one
bucket is nearly the same as the nested loops algo-
rithm. The most significant difference between the
two algorithms is that the hash join algorithm needs
to scan only a fraction of the buffered tuples resid-
ing in one bucket, and therefore, should have supe-
rior performance when the number of buckets is large,
whereas the nested loops algorithm needs to scan the
entire buffer.
3.2 Invalidation Costs
A key aspect of the windowed join operator, and for
that matter any windowed operator, is the invalidation
of the tuples that fall outside the window. Eventually,
the stale data that falls outside the window must be
removed in order to preserve system resources and to
ensure correct results. In the steady state, the rate of
tuples falling outside the window should on average
be equal to the rate of new tuples entering the system.
Therefore, the invalidation strategies for windowed
algorithms differ only in when they invalidate and not
in the rate at which they invalidate. Approaches for
invalidating stale tuples range from greedy to lazy
strategies. Greedy strategies attempt to remove stale
tuples as soon as possible, whereas lazy strategies de-
lay removal until an appropriate time.
In the case of the windowed hash join algorithm
invalidation occurs at the arrival time of a tuple on
an input. The greedy approach is to invalidate every
bucket at this time, while the lazy approach is to in-
validate only the bucket about to be probed. The
greedy approach ensures optimal memory usage since
no stale tuples are allowed to accumulate between ar-
rivals. The lazy approach allows stale tuples to build
up in a bucket until that bucket is probed. In gen-
eral, the average number of tuples that build up in a
bucket is the product of the time interval between in-
validations and the rate that tuples enter that bucket. If
invalidation occurs only at probe time, then the num-
ber of stale tuples that build up in buffer B is λ
B
/λ
A
as the time between probes is the time between the
ANALYTICAL AND EXPERIMENTAL EVALUATION OF STREAM-BASED JOIN
157

arrivals on stream A, N
B
/λ
A
, and the rate that tu-
ples enter the bucket λ
B
/N
B
. Here N
B
is the num-
ber of hash buckets for stream B. Thus, significant
accumulation of stale tuples occurs only if the rate
of the probe stream is small compared to the rate of
the arrival stream. An intermediate strategy is to in-
validate a bucket at both probe time and at insertion
time. Since the rate of either insertion or probe is the
sum of the individual rates, the average number of
stale tuples that accumulate between invalidations is
λ
B
/(λ
A
+ λ
B
), implying that large buildups of stale
tuples should not occur even if the rates of the streams
differ considerably.
The time cost of invalidation itself depends on the
algorithm. For our implementation of the windowed
hash join, the circular buffer structure of the hash
bucket results in efficient invalidation as stale tuples
can accumulate only at the bottom of the buffer. Thus,
the total number of comparisons needed is 1 + N
stale
as at least one comparison is needed with the first
non-stale tuple. The term N
stale
denotes the number
of stale tuples. The higher time cost of the optimal
greedy invalidation strategy is the cost of performing
at least one comparison with a tuple in every bucket.
The trade-off between greedy and lazy invalidation is
thus one of space versus time.
4 EXPERIMENTAL EVALUATION
In this section, we present our experimental evalu-
ation of the two join algorithms, windowed nested
loops (WNL) join and the windowed hash (WHJ)
join.
4.1 Experimental Setup and
Methodology
The windowed nested loops join and hash join algo-
rithms were implemented in C++ and evaluated on
Dell 2.0 GHz Pentium 4 workstation with 512MB
of memory. A batch of tuples was prepared and
processed en mass and the total processing time mea-
sured. The size of a batch is determined directly to
simulate the desired input rate. All tests were per-
formed for a batch of 60 seconds worth of tuples and a
time window of 30 seconds for both inputs. Only the
last 30 seconds worth of tuples were timed in order
to allow the buffers to reach steady-state conditions.
For the comparison measurements, the selectivity of
the join was set to 0.01 and the number of hash buck-
ets set to a corresponding value of 100. In addition
to the total processing cost, the effect of tuning the
hash bucket algorithm to match the selectivity to the
number of hash buckets was measured. Finally, the
effectiveness of invalidation strategies with respect to
memory and processing time were also measured.
4.2 Performance Measurements
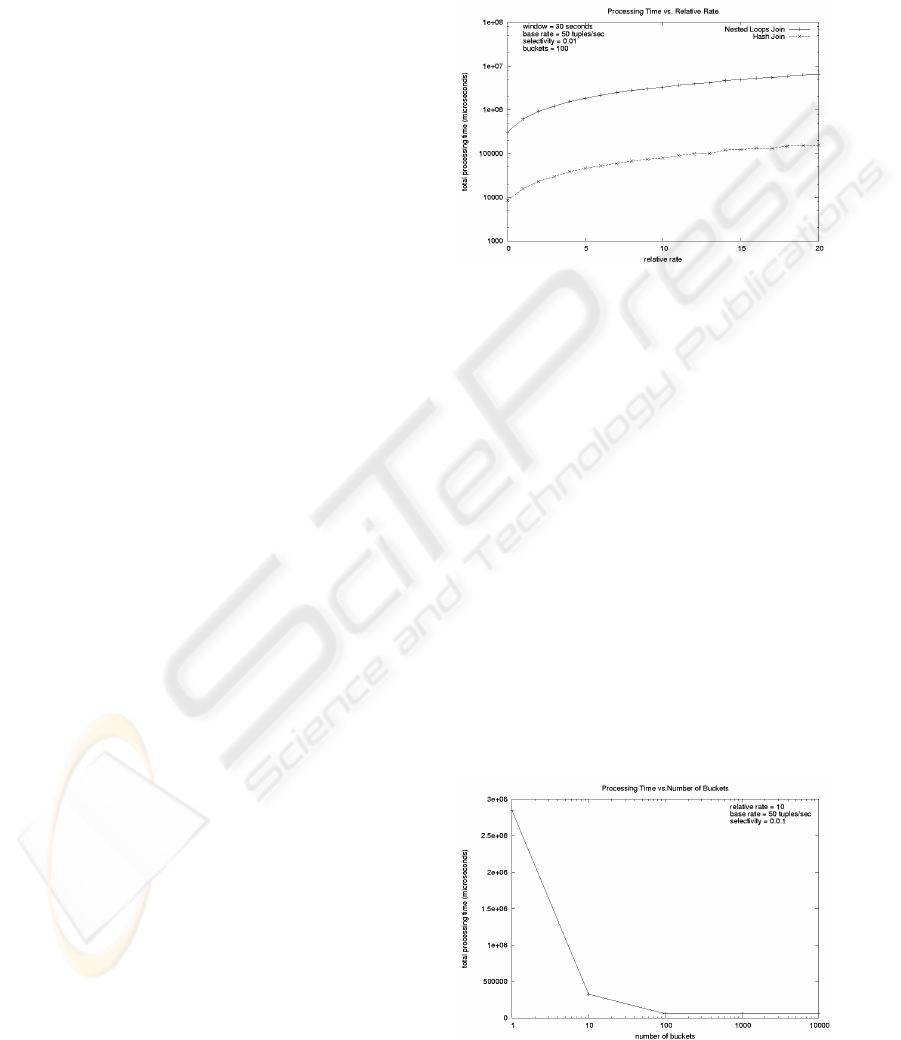
Figure 4: Performance of the Windowed Nested Loop and
Windowed Hash Join with Respect to the Relative Rate of
the Input Streams.
Figure 4 shows the performance difference be-
tween WNL and WHJ for 100 buckets. The two order
of magnitude difference indicates that the cost to scan
buffers for matches is the dominating cost. The cost
formulas (Equations 1 and 2) show that this cost is in-
versely proportional to the number of buckets (100 in
this case), and the measurements bear this out. Fig-
ure 5 shows that the total processing time is inversely
proportional to number of buckets (everything else
held constant). Note that when the number of buck-
ets is greater than the number of distinct values of the
join attributes, there is no longer any advantage to in-
creasing the number of buckets. The graph shows the
flattening occurs at 100 for selectivity 0.01 (implying
100 distinct join values) as expected. Note that this
flattening out effect is not captured by the cost for-
mula given in Equation 2.
Figure 5: Performance of the Windowed Hash Join with Re-
spect to the Number of Hash Buckets.
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
158

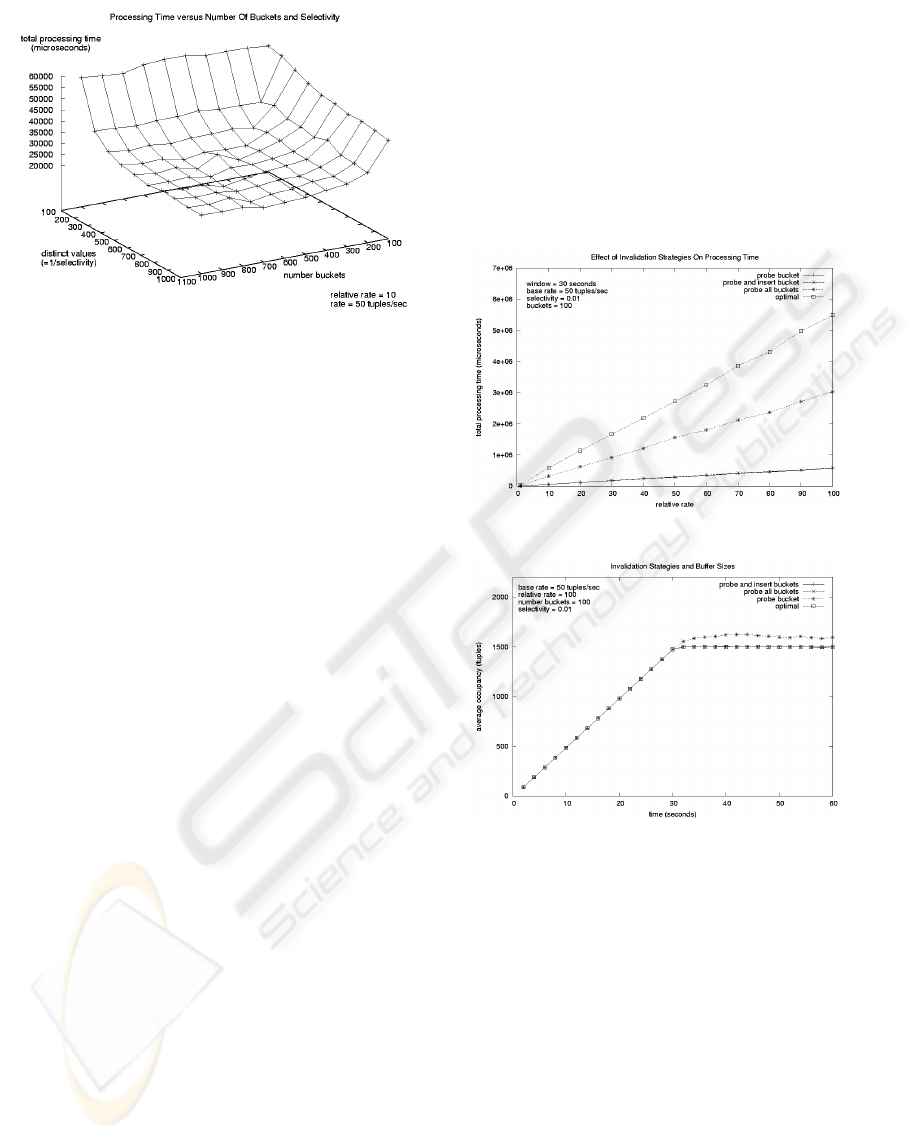
Figure 6: Performance of the Windowed Hash Join with Re-
spect to the Join Selectivity and the Number of Hash Buck-
ets.
Figure 6 depicts total processing time of the win-
dowed hash join for different values of selectivity and
number of hash buckets, and also shows that flatten-
ing occurs approximately when the number of buckets
equals the number of distinct hash values.
The effect of using extra invalidation in the hash
join algorithm was also measured. We measured the
processing cost and the memory utilization of four in-
validation strategies. The four strategies are described
as follows. Probe time invalidation is the minimal
invalidation required for the algorithm’s correctness,
and consists of removing stale tuples from the probed
hash bucket only whenever a tuple arrives on any in-
put. Probe and insert time invalidation removes stale
tuples from the probed and the insertion hash buckets,
in addition to the minimal invalidation of the probe
time invalidation strategy. The next two invalidation
strategies, called probe all buckets and optimal, re-
move tuples from all hash buckets on the probe side
only and all hash buckets on both the probe and in-
sertion sides respectively. Figure 7 shows the total
processing time of the four strategies. We see that the
probe and insert invalidation strategy does as well as
minimal invalidation strategy, i.e., the probe time in-
validation strategy. Both these strategies substantially
outperform the two greedy strategies that invalidate
all buckets.
Finally, Figure 8 shows the memory costs of the
four invalidation strategies. In these experiments, the
stream on the probed side had a relative rate 100 times
the rate of the opposite arrival side stream, and the
average occupancy of the entire set of all the hash
buckets on the probed side was measured every 2 sec-
onds for 60 seconds. We note that the steady state
conditions were reached after 30 seconds, which is
expected given a window size of 30 seconds. Ad-
ditionally, we note that, with the exception of probe
time invalidation, all the other strategies had approx-
imately the same average memory usage. In particu-
lar, the probe and insert time invalidation performed
as well as optimal invalidation strategy. Given the su-
perior processing time performance in Figure 7 and
its memory consumption, we conclude that the probe
and insert time invalidation provides the best choice
both for performance and memory consumption un-
der steady state conditions.
Figure 7: Processing Costs Of Four Invalidation Strategies.
Figure 8: Average Memory Occupancy of Hash Table
Buffers For Four Invalidation Strategies.
5 RELATED WORK
Recent years have seen a flurry of activity in streams
and continuous queries. We briefly describe three
pure stream databases that are being implemented,
the Aurora system(Carney et al., 2002), the STREAM
system(Arasu et al., 2002) and the Gigascope sys-
tem(Cranor et al., 2002). The Aurora project(Carney
et al., 2002) proposes an architecture for a stream
database system based on a data flow architecture.
The user of the Aurora system designs a query by
manipulating a diagram of the query in a GUI. The
query is built from boxes that represent individual
ANALYTICAL AND EXPERIMENTAL EVALUATION OF STREAM-BASED JOIN
159

operations on a stream. The boxes are analogous
to the relational operators in a relational system and
the diagram of boxes analogous to a relational query
plan. However, there is no higher level declarative
query language analogous to SQL to compose these
queries. The operators themselves perform filtering
operations (which require no buffering) and window-
ing operations (which require buffering). The notion
of a window is extended to include slides, latches, and
tumbles. Slide moves a window continuously down-
stream, tumble moves a window discontinuously so
that consecutive windows share no tuples, and latch
moves a window like a tumble but also keeps state
information between positions of the window. The
analysis presented in this paper can be easily extended
to slide, tumble and latch windows.
STREAM is a design for a stream database sys-
tem currently being constructed at Stanford Univer-
sity(Arasu et al., 2002). The STREAM system is
designed to be a conservative extension of relational
database concepts. They provide an SQL-like query
language, CQL, with extensions for windowing and
other stream primitive operators, a semantics based
on mapping CQL to relational tables, and an imple-
mentation architecture based on a dataflow paradigm.
A CQL query is parsed into a query plan consisting
of a tree of stream operators. Synopses are general
data structures associated with an operator that main-
tain any state needed by an operator to compute cor-
rect results. The query plan can then be optimized
both statically at compile time and dynamically at run
time. Most of the reported optimization strategies at-
tempt to minimize total memory requirements. Our
analysis goes along the lines of the STREAM(Arasu
et al., 2002) work and the analyzes the memory re-
quirements for the different invalidation strategies a
key factor when dealing with windowed operators.
Gigascope is a network performance monitoring
tool that incorporates stream database ideas in its im-
plementation(Cranor et al., 2002). The kinds of com-
plex queries that users typically wish to make against
network data streams are difficult or impossible to ex-
press in SQL. Ordering tuples from a data stream by
time stamp is not sufficient since, for example, ses-
sion information may present a different order than
the time of arrival. Therefore, the notion of order
in a stream needs to be extended. The implications
of this extension for stream database operators are
numerous. The most important is that buffering re-
quirements are increased since the determination of
when to discard stale data is no longer directly tied
to time. For example, in a windowed join operator,
if one stream stalls the other may need to have un-
bounded buffers while waiting for new data to arrive
on the stalled stream. Extending the definition of or-
der may help optimization, since there is more room
to play with in the implementation of an operator: dif-
ferent operator implementations may produce differ-
ent ordering properties in the output. Gigascope im-
plements some of these new ordering definitions into
its operators. The Minimum Memory join algorithm
presented in (Cranor et al., 2002) is similar to our win-
dowed nested loops join (WNL) algorithm presented
in Section 2, and as such our analysis of the invalida-
tion strategies can be applied.
Viglas et al.(Viglas and Naughton, 2002) in their
work have presented brief discussions on non-
blocking, windowed versions of nested loops join and
symmetric hash join algorithms for the implementa-
tion of the windowed join operator. Although our ap-
proach is based on the cost model proposed by Viglas
et al.(Viglas and Naughton, 2002), our work differs in
three ways. First, our version of the windowed nested
loops join differs from the one presented in (Viglas
and Naughton, 2002) in its invalidation process. In
particular, the Viglas nested loops join(Viglas and
Naughton, 2002) does not invalidate the opposite win-
dow on arrival of a tuple and therefore can output join
tuples that are not strictly within the window. Sec-
ond, while Viglas et al.(Viglas and Naughton, 2002)
provide some discussion of a hash join, the algorithm
itself is not presented. We explicitly present a win-
dowed hash join in this paper. Third, we directly
compare our results to those reported in (Viglas and
Naughton, 2002). A significant difference between
the two results is the quadratic dependence on the in-
put rate as discussed in(Viglas and Naughton, 2002)
for the windowed hash join. We did not observe the
same quadratic dependence. Rather, our implementa-
tion provides a linear dependence to the input rate (in
the half-cost analysis) for our implementation of win-
dowed hash join. We further provide an analysis of
both the performance and the memory requirements
of the different invalidation strategies.
6 CONCLUSIONS AND FUTURE
WORK
In this paper we have presented analytical and ex-
perimental evaluation of two implementations of a
windowed join operator. The results clearly show
that the windowed hash join is superior to windowed
nested loops join based on an average cost per unit
time. Both analysis and measurement yield this re-
sult. We also compared our results to those reported
in (Viglas and Naughton, 2002). A significant differ-
ence between the two results was the quadratic de-
pendence on the input rate as discussed in(Viglas and
Naughton, 2002) for the windowed hash join. We did
not observe the same quadratic dependence. Rather
our implementation uses circular buffer based hash-
buckets to provide linear performance. It should be
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
160

noted however that the circular buffer approach is ap-
plicable only when the tuples are ordered by arrival
time stamp. We also examined the cost of lazy and
greedy invalidation strategies for both windowed join
algorithms and examined both the processing cost as
well as the memory requirements for both invalida-
tion schemes. It should be noted that the analysis of
the invalidation strategies can be easily extended to
apply for any windowed operator.
In terms of continuing work, while in this paper
we have presented implementations of the windowed
join operator, we have found that this join operator is
not associative and it relies on strict order of arrival
time alone. In general we have found that precisely-
defined stream operator algebra that can be used to
express well-defined stream queries – much in the
same way that the relational algebra defines relational
queries – is not found in the stream database litera-
ture. Each system implements their own set of opera-
tors but does not provide a way to describe the compo-
sition of operators. The general problem of the com-
position of stream operators is difficult. One would
like to have operators that would take stream inputs
with well-defined properties and produce stream out-
puts with well-defined properties in such a manner
that the resulting composition algebra is simple. That
these goals may conflict can be seen from a consider-
ation of the window join operator. If the output of the
window join operator is ordered by the time stamp
of one of its composite tuples, then neither choice
will lead to an associative window join operator. Per-
haps the closest well-defined stream semantics and
query language are those proposed by the Stanford
STREAM project(Arasu et al., 2002). These seman-
tics depend upon mapping stream queries onto the
standard relational semantics. However, no stream
operator definitions are given that may implement
the proposed stream semantics(Arasu et al., 2002).
We are now working on defining a pure stream alge-
bra that addresses these problems and provides well-
defined stream semantics.
REFERENCES
Arasu, A., Babu, S., and Widom, J. (2002). An Ab-
stract Semantics and Concrete Language for Contin-
uous Queries over Streams and Relations. Technical
report, Stanford University.
Babcock, B., Babu, S., Datar, M., Motwani, R., and Widom,
J. (2002). Models and Issues in Data Stream Systems.
In Principles of Database Systems (PODS).
Babu, S. and Widom, J. (2001). Continuous Queries over
Data Streams. In Sigmod Record.
Carney, D., Cetintemel, U., Cherniack, M., Convey, C.,
Lee, S., Seidman, G., Stonebraker, M., Tatbul, N., and
Zdonik, S. (2002). Monitoring Streams - A New Class
of Data Management Applications. In Int. Conference
on Very Large Data Bases, pages 215–226.
Chen, J., DeWitt, D., Tian, F., and Wang, Y. (2000). Ni-
agaraCQ: A Scalable Continuous Query System for
Internet Databases. In SIGMOD, pages 379–390.
Cranor, C., Gao, Y., Johnson, T., Shkapenyuk, V., and
Spatscheck, O. (2002). Gigascope: High Performance
Network Monitoring with an SQL Interface. In SIG-
MOD, page 623.
Motwani, R., Widom, J., Arasu, A., Babcock, B., Babu, S.,
Datar, M., Manku, G., Olston, C., Rosenstein, J., and
Varma, R. (2003). Query Processing, Resource Man-
agement, and Approximation in a Data Stream Man-
agement System. In Conference on Innovative Data
Systems Research.
Ullman, J. and Widom, J. (1997). A First Course in Data-
base Systems. Prentice-Hall, Inc.
Viglas, S. and Naughton, J. (2002). Rate-based Query Opti-
mization for Streaming Information Sources. In SIG-
MOD, pages 37–48.
ANALYTICAL AND EXPERIMENTAL EVALUATION OF STREAM-BASED JOIN
161