A THEORETICAL PERFORMANCE ANALYSIS METHOD FOR

BUSINESS PROCESS MODEL

Liping YANG, Ying LIU, Xin ZHOU

IBM China Research Lab

Keywords: Computational Model, B

alance Equation System, Bottleneck, Business Process Model

Abstract: During designing a business process model, to predict its performance is very important. The performance

of business operational process is heavily influenced by its bottlenecks. In order to improve the

performance, finding the bottlenecks is critical. This paper proposes a theoretical analysis method for

bottleneck detection. An abstract computational model is designed to capture the main elements of a

business operational process model. Based on the computational model, a balance equation system is set up.

The bottlenecks can be detected by solving the balance equation system. Compared with traditional

bottleneck detection methods, this theoretical analysis method has two obvious advantages: the cost of

detecting bottlenecks is very low because they can be predicted in design time with no need for system

simulation; and it can not only correctly predict the bottlenecks but also give the solutions for improving the

bottleneck by solving the balance equation system.

1 INTRODUCTION

In order to keep competitive in the marketplace,

enterprises have to continuously increase the

performance while reducing the cost. Business

process modeling represents the business logic of an

enterprise’s business activities. It includes mainly

three kinds of important components: activities, data

processed by activities and resources allocated to or

consumed by activities. Performance of business

processes running in an enterprise influences heavily

on performance of the whole enterprise. As a result,

it is effective to improve enterprise performance by

accelerating its business processes.

A large number of experiences accumulated in

business

practice indicate that keeping compatible

data processing speed of relative activities and

appropriate allocation of resources are two major

factors for high performance. Otherwise,

performance bottlenecks constraint the whole

process performance. Given a manufacturing

enterprise that has a high-speed producing

department and a low-speed sales department, it will

have to stop operating due to the overflow

warehouse sooner or later. Once the root cause

behind this phenomena is detected, the enterprise

can adjust the produce-store-sale process to gain the

producing speed, sales speed and warehouse

capacity suited by re-allocating resources. However,

detecting business process bottlenecks is usually

time consuming and prone to be inaccurate because

of the complexity of business process and the

inherent hidden characteristics of bottlenecks.

Therefore, an effective and accurate approach is

urgently needed to detect the bottlenecks in business

process for performance improvement.

There are currently a lot of methods in use to detect

e bottlenecks(Christoph, 2003)(Christoph, 2001)

(Blake, 1995)(Lawrence, 1995). Two frequently

used methods are measuring waiting time and

calculating the utilization. Waiting time method is to

look for the machine where the parts have to wait for

the longest time. A common method is to look for

the longest queue. However, this approach works

only for linear systems containing only one type of

part. The utilization based method is to measure the

percentage of the time that a machine is active, and

then define the machine with the largest active

percentage as the bottleneck. Both of these two

approaches have several drawbacks.

For measuring waiting time, the accuracy of this

approach is c

ompromised if the system contains

YANG L., LIU Y. and ZHOU X. (2005).

A THEORETICAL PERFORMANCE ANALYSIS METHOD FOR BUSINESS PROCESS MODEL.

In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 73-80

DOI: 10.5220/0002537700730080

 SciTePress

buffers of limited size. Furthermore, this approach

analyzes only the processing machines of the

manufacturing system. Other elements, such as

human workers, supply and demand, do not have the

concept of buffer, so that the waiting time measuring

approach is not feasible for them. For measuring

utilization, the measure result may be not accurate

enough to be trusted because the difference between

the utilizations of the machines may be very small.

While this method is easy to be automated, the

results are not always accurate (Luthi, 1997).

Moreover, most of utilization bottleneck detection

methods are based on analyzing the system data in

running time or simulating the systems, which will

result in great cost and time consuming.

In this paper, an abstract computational model is put

forward aiming at analyzing business process

performance effectively and efficiently. Firstly, a

computational model is proposed to abstractly model

business process as sets of transitions, data, data

buffers, and connections between transitions, based

on which most of the common performance related

problems are described. Then, the problem of

analyzing bottleneck transitions in a business

process is theoretically induced as a Balance

Equation solving problem and a solving algorithm

for Balance Equation is proposed. Finally, real

business performance problems are analyzed using

above theoretical method to illustrate the application

of this approach and verify its effect.

We start presenting the computational and analytical

model in Section 2. Section 3 introduces the

theoretical foundation, Balance Equation System, for

business transition bottleneck detection and proposes

the equation solving algorithm. Performance

problems in real case are dealt with in Section 4 for

illustrating and verifying the whole approach.

Section 5 concludes this paper and gives direction of

the future works.

2 THE COMPUTATIONAL

MODEL

To perform performance analysis, it’s necessary to

firstly abstract the system as a mathematical model.

Such mathematical models keep critical elements

but eliminate those unnecessary details. As a result,

we can focus on the perspective closely related to

the problem we concern. At the same time, we can

utilize some mathematical mechanism to detect the

bottleneck conveniently and accurately. A lot of

theoretical models can act this role, for example,

queue network(Donald, 1998), Petri Net(Ajmone,

1984)(Baccelli, 1993)(Salimifard, 2001), fluid

model(Kelly, 2004) etc. However, all these models

are not specially designed for analyzing the

performance of business process model. They are

complex and not easy to be used in the business

process bottleneck detection.

To simulate the behavior of a business process and

support further mathematical performance analysis,

we use a computational model defined in Definition

2.1. In our definition, four kinds of elements are

taken into consideration: transitions, data,

connections and data buffers. Transitions are

abstraction of activities in a business process, which

perform data processing in a certain period of time.

Data are abstraction of business items processed by

business process activities. The basic unit of data is

a data particle, which can be a group of transaction

data with fixed composition structure in a business

process. A connection is a directed linkage between

two transitions representing that output data from the

source transition provides input data for the target

transition. A data buffer is associated with a

connection to cache data for dealing with the run

time un-synchronization between two connected

transitions. A transition is periodically executed on a

fixed time interval. In case that one of the input

buffers is empty or an output buffer is full, the

current transition operation is skipped. Later, after

the time interval, the transition engine will come

again to see if the transition can be performed.

Definition 2.1 A Computational Model is a tuple (T,

C, B, Start, End, I/O, V

, V

), where,

1) T is a set of transitions. 2)C is a set of connections

that connect two transitions. 3)B is a set of data

buffers. Each data buffer may store multiple data

particles. 4)Start is a set of initial data buffers, and

the size of these buffers is supposed to be infinite.

5)End is a set of final data buffers, and the size of

these buffers is supposed to be infinite. 6)I/O is a

finite set. Each of the elements in the set is called a

data input/output structure (D-I/O-S) which is

defined for an individual transition. A D-I/O-S is

denoted as the following form: T

: ( ) -> (

where T

is the transition, is the consumed data

particles by transition X, and

is the produced

data particles. For example, T

: (1,2,2) -> (3,4)

means that each time transition T

consumes three

types of data particles and the number of each type

separately is 1, 2, and 2, and produces two types of

data particles and the number is 3 and 4. 7) V

is a

set of running speeds of all the transitions. 8) V

is a

set of effective speeds of all the transitions.

ICEIS 2005 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

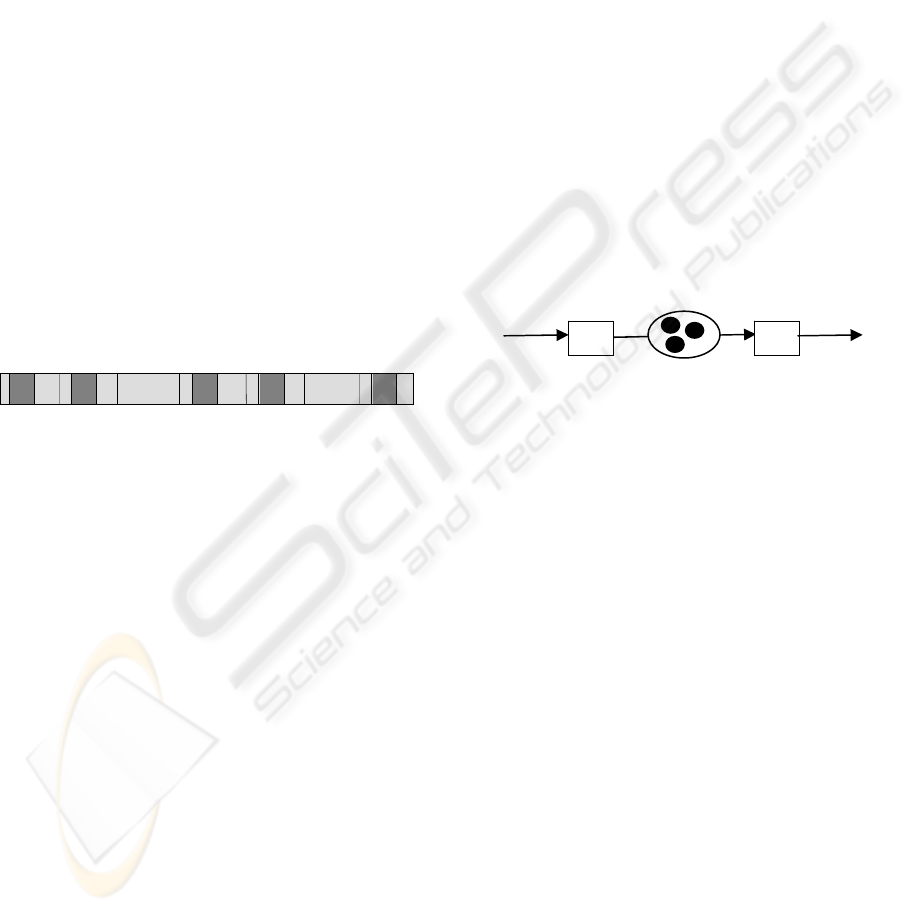
For a transition, there are two important concepts

regarding its performance analysis: the running

speed V

of a transition and the effective speed V

of a transition. V

indicates the speed that the

transition accesses the input buffers in order to

perform an operation, i.e., the number of times that

the transition accesses the input buffers trying to

extract data particles from them within a time unit. It

should be noticed that not every attempt to extract

data particle can be accomplished. An attempt may

fail due to empty input buffer or fill-up output buffer.

indicates the speed that the transition accesses

the input buffers, gets data particles successfully,

and performs data processing, and writes data into

output buffers. From the definition, it obviously

holds V

≤

Figure 2.1 shows the status of a running transition.

In which the light-grey blocks indicates the pace of

running, while the dark-grey blocks show the pace

of processing. For the yellow block with red one in

it, that is the case that the operation fails to meet the

requirement for performing a transformation. The

ratio V

represents the power usage of the

transition. The above two speeds are about the

average running speed. In the real world situation,

these speeds may vary with time.

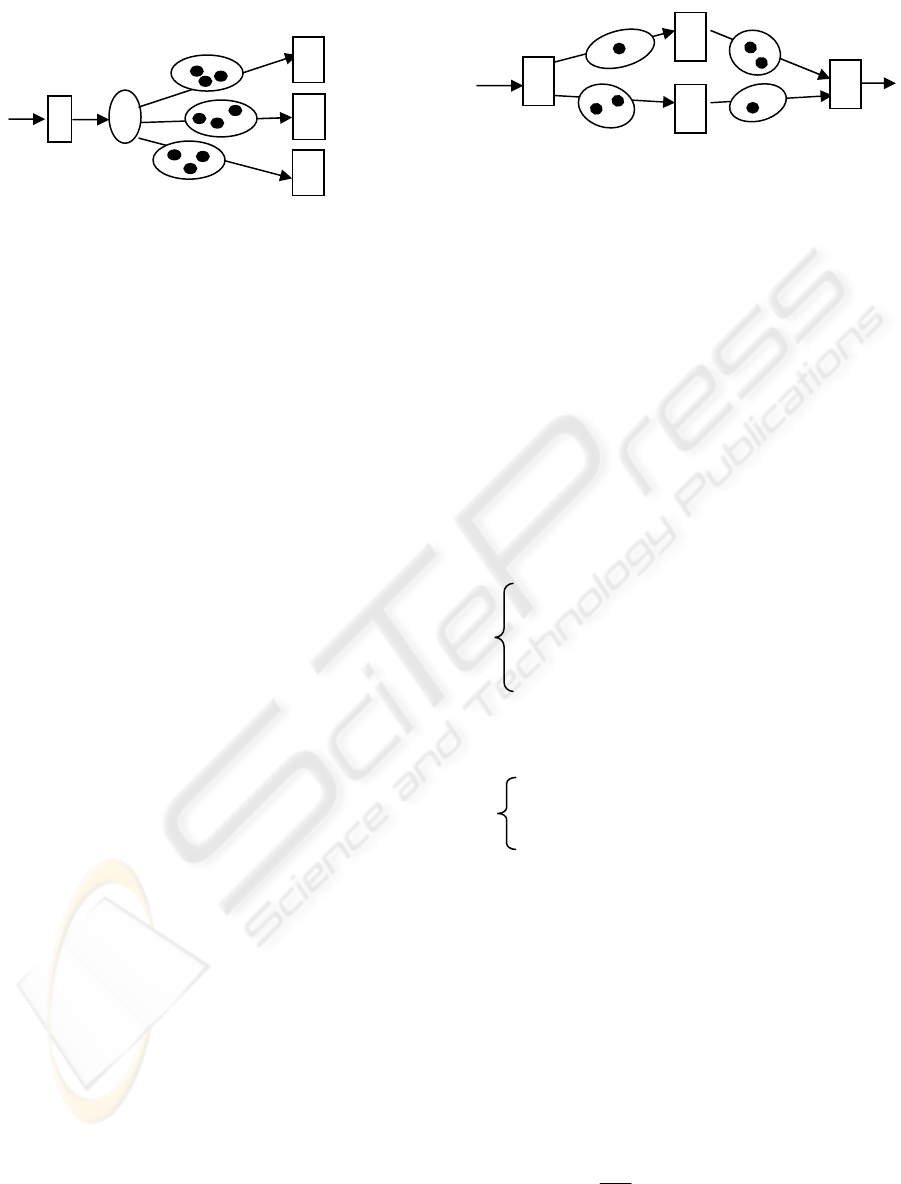
Choice transition is a special kind of transition as

denoted in Figure 3.2. It is used to represent multiple

output choices for a transition. For the transition A,

there are three possible output paths connecting with

different next transitions. The transition C in the

diagram is the choice node. It is associated with

some judgment criteria in order to decide which

connection the data should move with. It should be

noticed that there is no buffer over the A-C

connection. This is because a choice node is treated

as a kind of super fast transition unit, such that every

input data will be passed to the next level

connections with no time delay.

3 THEORETICAL ANALYSIS

METHOD

The essential capability of process model is to

specify the behavior of a real business process. An

individual transition represents a behavior of a

business activity, and the execution logic of a set of

transitions is used to capture the behavior

environment of a business process. The performance

of a business process can be scaled by different

approaches, such as throughput of an activity and

task waiting time. In this paper, data throughput is

regarded as a performance scale standard for a

business process. That it to say, the more data is

manipulated within a time unit, the higher

performance of the business process will be.

For a business process, the execution logic structure

of its activities is usually known, which indicates

that the data input/output capability of each activity

in the process is known. This structure is defined as

data input/output structure of computational model.

Based on the above conditions, we can analyze the

global performance of the process model, so that the

analysis result can help design the running speed of

each activity and the size of every data buffer. In

order to analyze the performance of process model,

we designed a balance equation system (BES).

Based on BES, a lot of performance related business

problems can be solved.

3.1 Balance Equation System (BES)

A B

Figure 3.1 Sequential Structure.

Figure 3.1 is a simple Computational Model with

sequential execution logic. It includes two

transitions, A and B, and a data buffer C. The data

input/output structure of transition A is A: (N

>(M

), and the data input/output structure of

transition B is B: (N

)->(M

). Suppose the

running speed of transition A and transition B

separately are V

and V

. For data buffer C, when

transition A puts V

particles into the buffer,

transition B will extract V

particles from the

buffer in the same time unit. In order to guarantee

the process can be safely and normally executed in a

long time, the V

and V

must be equal.

Otherwise, the buffer C will produce two situations:

one is the process is blocked because the buffer C is

full; and the other is transition B is idle because the

buffer is empty. The following is called Balance

Equation for buffer C:

Figure 2.1: Status of a running transition

= V

Where 0

≤

and 0

≤

(3.1)

Where, V

and V

are the effective speeds of

transition A and B respectively; U

and U

are the

upper bounds of V

and V

respectively. At the

design time of a model, U

and U

are parameters

for consideration. In the run time, U

and U

should

A THEORETICAL PERFORMANCE ANALYSIS METHOD FOR BUSINESS PROCESS MODEL

and respectively.

Figure 3.2 is a Computational Model with a choice

execution logic. The data input/output structure of

transition A is A: (N

)->(M

), and the data

input/output structure of transition B

(i=1, 2, 3) is

denoted as B

: (N

ABi

)->(M

BiY

)

So the Balance

Equation is as following:

ABBAAi

NVMV =

3,2,1

i (3.2)

∑

(3.3)

The above Balance Equations describe the basic

feature of the data particle flow over the

computational model. All the balance equations of a

computational model is called the Balance Equation

System of the model.

Properties: The following are some basic properties

of the balance equations.

1) There are exactly two non-zero elements

for each equation.

2) V=0 is a solution.

3) The solution set is convex.

In most cases, it holds in the model that the number

of connections is larger than the number of

transitions. This indicates that the BES is usually

over constrained.

Definition 3.1: The computational model is called

consistent if there is a non-zero solution for its BES.

3.2 Solvability of the BES

For any Balance Equation, we are going to study

what is the condition that it has non-trivial solution.

In order to give a general conclusion, an example is

used to illustrate the main idea. Figure 3.3 is an

example of Computational Model. It includes four

transitions, four data buffers, and four connections.

From transition A to transition B, there are two

paths, A-C-B and A-D-B.

The data input/output structures of transition A, B,

C, D separately are:

A: (N

)->(M

, M

);

B: (N

, N

)->(M

);

C: (N

)->(M

);

D: (N

)->(M

)

(MAC, MAD) denotes that transition A outputs data

MAC and MAD in parallel. MAC is for path A-C,

and MAD is for path A-D. (NCB, NDB) denotes that

transition B can be executed only accepting two

inputs from two paths in parallel. NCB is from C-B,

and NDB is from path D-B. The balance equation

system of this computational model is given as

following:

= V

(3.4)

= V

(3.5)

= V

(3.6)

= V

(3.7)

From the above balance equations, the following

two equations can be gotten:

BCBACCACA

VVV

(3.8)

BDBADDADA

VVV

(3.9)

, where α = N/M is called transforming parameter of

transition X and transition Y, and N is the data input

of transition Y, and M is the data output of transition

X. Comparing (3.8) and (3.9), we can get the

consistency condition for equations (3.4)-(3.7) to

have non-zero solution as:

DBADCBAC

(3.10)

Definition 3.2: Given a path in the computational

model, T

->T

->…->T

, the transforming

parameters of this path are defined as

αi =

∏

(i=1, 2, …, L),

Figure 3.3: Computational Model Example

Figure 3.2: Choice Structure

ICEIS 2005 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

where Ni+1 is data input of transition T

i+1

, and M

the output data of transition T

From the above example analysis, the following

theorem is easy to be understood.

Theorem 3.1: The BES has non-trivial solution if

and only if that for any two connected nodes on the

model, all the paths connecting the two nodes have

the same transition parameter.

Example 3.1: For the computation model in Figure

3.3, suppose its data input/output structure has the

following two situations, and the running speed of

every transition is (A,B,C,D)=(1,1,1,1):

A: (1)->(2,1); B: (1,1)-> (1);

C: (1)-> (1); D: (1)-> (1)

A: (1)->(2,1); B: (1,1)-> (1);

C: (1)-> (2); D: (1)-> (1)

For situation (1), the balance equation system is as

following:

= V

Obviously, it has no solution for these equations.

The transforming parameters of path A-C-B are

, and the transforming parameters of path A-

D-B are

. These parameters are not the same.

For situation (2), the balance equation system is as

following:

= V

Then, we can solve the solution vector: (VA, VB,

VC, VD) = λ(0.5, 1, 1, 0.5), where 1 ≥ λ ≥ 0.

Similarly, we can get the transforming parameter of

path A-C-B as

, and

is the transforming

parameter of path A-D-B. Their parameters are the

same.

Theorem 3.1 gives the theoretical statement on the

feasibility of a computational model, which is the

very fundamental rule for designing a computational

model. In fact, a model with trivial solution is

equivalent to that the model can not run safely in a

long time. The above analysis on the transition

parameter also tells the following result.

Lemma: For any two nodes A and B in the model, if

they are connected and the BES has non-trivial

solution V, then the value V

is a constant which

is independent of different solutions of the system.

Theorem 3.2: If every two nodes on the model is

inter-connected, then the solution for BES is unique

in the sense that for every two solutions there is a

constant C ≥ 0, such that V

= CV

Based on theorem 3.2, the vector

VVV =

∧

is denoted

as the unit solution of the BES.

Proposition: If the model is connected, it holds Vi >

0 for all i=1, 2, n, where V is a non-trivial solution

for BES.

3.3 Algorithm for Solving BES

Algorithm for solving BES

INPUT:

the transition number is n of this computational model;

data input/output structure T

: (N

)->(M

);

the running speed of every transition T

is U

;

N is the number of transitions in the computational

model;

OUPUT:

effective running speed V

of every transition T

Begin

for i=1,2,…N

initialize the value by setting V

= U

endfor

while ( there is a V

changed ) do

for i = 1, 2,…,N

for j = 1, 2,…N

if ((Connection(Ti,Tj) and (V

< V

))

then

= (V

-V

) / N

// such that V

= V

endfor

for k = 1,2,…N

if ((Connection(Ti,Tj) and (V

> V

))

then

=( V

- V

) / M

// such that V

= V

endfor

endwhile

Return V

End

Figure 3.4: BES Solving Algorithm

A THEORETICAL PERFORMANCE ANALYSIS METHOD FOR BUSINESS PROCESS MODEL

The algorithm in Figure 3.4 is an iterative one which

will solve the BES. In the algorithm, Vi indicates the

effective speed of the i-th node in the model. For a

given node, Vj is the speed of its j-th input node, and

Vk is the speed of its k-th output node.

In this algorithm, if a Vi converges to zero, which

indicates all of Vi converges to zero, then the model

does not have a non-trivial solution. During the

computation process in the above algorithm, VM

and VN is monotone descending, therefore, Δ Vi ≥ 0

and Δ Vi ≥ 0. If a Vi keeps unchanged during the

whole process of the algorithm, then this Vi is a

bottleneck node for the model.

3.4 Bottleneck Transition Analysis

In the equation (3.1), each variable V

has an upper

bound U

. In the language of computational model,

is the effective speed of the transition T

and U

the running speed of it. Each solution

for the BES

represents a group of steady solution for the

performance of transitions on the model. If the

effective speed of a transition is the first one to

approach to its upper bound while others remain

below their upper bounds, this transition is called the

bottleneck of the system. It is possible that a system

has more than one bottleneck.

Using theorem 3.2, the problem of finding the

maximum system performance becomes the problem

of solving

from following equation,

(3.11)

)(max

max

= VV

∧

, where

is used to dented the solution vector of a

BES is a solution of a BES, and λ ≥ 0, so

that

∧

UV ≤≤

Suppose

is a constant which can be applied to

(3.11). From above analysis, we can get that the

bottleneck transitions for the computational model

are those transitions T

such that

(3.12)

UV =

∧

When the model is running at its maximum

performance, only the transitions satisfying (3.12)

can reach its maximum performance such

that

. For other transitions, it

holds

. The power usage rate of transition T

VV =

VV >

∧

(3.13)

From (3.13), it can be seen that only the bottleneck

nodes can reach their maximum power usage. For

example 3.1, if its data input/output structure is

situation (2), its bottlenecks have two transitions, B

and C, because their utilizations are the highest.

At the run time of the model, if all of the bottleneck

nodes are the input and output nodes, it indicates

there is potential to improve the performance of

system by improving the IO performance only.

Otherwise, improving the system performance will

have to depend on better system node performance

or better system structure.

4 APPLICATIONS OF

BOTTLENECK DETECTION

In real situation, there are a lot of business problems

caused by bottlenecks. However, these problems in a

real business process usually fall into some patterns.

In this section, we focus on two major patterns:

Input Data Flush pattern and Block Caused by a

Paused Transition pattern, and analyz them based on

the solution given above.

4.1 Analyzing Input Data Flush

In real business world, the volume of data input to a

business process varies from time to time and

usually large numbers of data suddenly flush into for

processing. We classify this kind of pervasive

running status as a pattern called Input Data Flush

pattern. For a business process in this pattern, it

really suffers from sudden flush of input data which

results in buffer jam, transition breakdown, and so

on. So it’s necessary to analyze and predict the

impact of flush input data and suggest some

approaches to counteract the negative effect. The

theoretical method proposed in Section 3 can be

leveraged to fulfill this demand.

Given a business process represented in

computational model as shown in Figure 4.1, and

suppose we have detect the bottleneck transition T

by solving the Balance Equation System of such

process, we can predict the operation behavior of

each transitions as below:

If transition T

is a subsequent transition of T

and

there is a path from T

to T

, then T

will be light-

load transition sooner or later since low performance

Ti will limit the input data volume of T

ICEIS 2005 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

If transition T

is a previous transition of T

and there

is a path from T

to T

, then firstly T

will be heavy-

load transition due to large input volume but

gradually slow down because of buffer jams on the

path from T

to T

There is another critical issue to be analyzed for this

pattern. If one trying to accelerate the bottleneck

transition Ti for better process performance, it seems

wonderful but in fact dangerous if no deep analysis

and extra step are taken. Given there is a high

performance transition T

i+1

that is the direct

subsequent transition of T

, the performance of T

i+1

is prevented from full release by bottleneck

transition Ti before T

’s acceleration, then the low

performance transitions after T

i+1

can run safely

without worrying about buffer jam. However, once

we accelerate T

, then T

i+1

can fully release its

performance and buffer jam might produce between

i+1

and its low performance subsequent transitions,

which will result in new round system block. By

further analysis based on solving the Balance

Equation System, we can decide the upper speed

limit for T

i+1

after T

’s acceleration so as to avoid

new round block and specially configure T

i+1

to meet

its upper speed limit.

4.2 Analyzing Block Caused by a

Paused Transition

When a transition of a process model is paused

because of exception, the process will be blocked.

However, the block will not immediately be

propagated to the whole process because the size of

data buffer is not zero. The block propagation will

spend some time. In a long time, the final result is

that all the system is paused. For this situation, we

called it a Block Caused by a Paused Transition

pattern which is specified with Figure 4.2. For this

pattern, it is difficult to detect the problem from the

superficial phenomenon. And it is not easy to

simulate all the situations because there are a lot of

transitions and large number of paths. We must

provide theoretical analysis methods to handle this

pattern.

On the one hand, it will be useful to predicate the

situation, so that we can know how to control it. On

the other hand, some methods should be provided to

repair the paused system once this situation happens.

No matter we are preventing or repairing the

problem, computing the running speed of the

transitions is the foundation. Based on the running

speed, we will provide a method about how to

compute block propagation time.

Suppose a transition T

i+1

is paused, the block will be

propagated backward along a path. If a connection

from transition T

to T

i+1

exists, and the size of data

buffer between them is

C , and the effective speed

of transition T

is λ

, and the data input/output

structure of transition T

is (N

)->(M

), then the

block propagation time from T

to T

i+1

Suppose T

->T

->…->T

n+1

is a path, and the T

n+1

the paused node, then the block propagation time

BPT(T

n+1

) from T

n+1

to T

can be computed using

the following formula:

BPT(T

) =

∑

According to the above formula, we can have the

following conclusion:

Bottleneck

…

i+1

…

Figure 4.1 Input Data Flush Pattern

Reverse block

ormal

Figure 4.2: Block Caused by a Paused Node

aused node

lock

ation direction

block here

A THEORETICAL PERFORMANCE ANALYSIS METHOD FOR BUSINESS PROCESS MODEL

1) If the value of

is smaller, which indicates the

system is running at low performance level, a

process will spend longer time to be fully blocked

once a node is paused;

2) If the data buffer is the larger, the block

propagation time will be longer.

5 CONCLUSION

Detecting and improving business process

bottlenecks are critical for enterprise performance

improvement. This paper aims at a quantitative

analysis method for effectively and efficiently

detecting business process bottlenecks. A

computational model is proposed to abstract key

elements in business process model, including

transition, data, buffer and connections. Based on

this computational model, a Balance Equation

System is put forward to detect bottlenecks and the

solutions about how to improve the bottlenecks are

given. Furthermore, this approach was used to some

concrete applications. We classified the common

applications into some patterns, including large

number input data impact, block caused by a paused

node. Through using the theoretical analysis method,

these application patterns can be solved well.

Compared with traditional performance analysis

method, the theoretical analysis method in this paper

is easier and much more practical.

In a real business process, the performance of a

transition (the running speed of the transition) may

not be a constant, but depends on the resource

allocated to it. The more resource is allocated, the

better transition node performs we will have. From

the resource allocation point of view, a critical

resource can be allocated to multiple transitions.

Many applications run on the same server is the

typical example for this, in which applications are

transitions and the CPU power of the server is the

resource. How to best allocate the limited resource

to make the system achieve the highest performance

is an important topic for further study. In another

situation, the system performance may not be able to

meet the business requirements even though each

individual transition has reached its maximum

performance. This raises the problem of system

structure optimization. The challenge here is how to

change the system structure (the connection

structure of the model) to meet a specific high

requirements on performance. Changing the

bottleneck node into a parallel sub-structure can be a

example for this kind of structure optimization. The

analytical power of computational model will

provide a solid foundation for dealing with this kind

of problems.

REFERENCES

Christoph Roser, Masaru Nakano, Minoru Tanaka, 2003.

Comparison of Bottleneck Detection Methods for AGV

Systems. Proceedings of the 2003 Winter Simulation

Conference.

R. Blake and J. Breese, 1995. Automatic Bottleneck

Detection, Microsoft Technical Report MSR-TR-95-

10, Microsoft Corporation, October 1995.

Luthi, J., and Haring, 1997. G. Bottleneck Analysis for

Computer and Communication Systems with Workload

Variabilities & Uncertainties. In Proceedings of 2nd

International Symposium on Mathematical Modelling,

ed. I. Troch and F. Breitenecker, 525-534, 1997,

Vienna, Austria.

Lawrence, S. R., and Buss, A. H. 1995. Economic

Analysis of Production Bottlenecks. Mathematical

Problems in Engineering, 1(4): 341-369.

Christoph Roser, Masaru Nakano, 2001. Minoru Tanaka.

A Practical Bottleneck Detection Method. Proceedings

of the 2001 Winter Simulation Conference.

Donald Gross & Carl M. Harris, 1998. Fundamentals of

Queueing Theory, Third Edition Wiley-InterScience,

1998.

M.Ajmone Marsan, G.Balbo , and G.Conte, 1984. A Class

of Generalized Stochastic Petri Nets for the

Performance Analysis of Multiprocessor Systems,

ACM Trans. Computer Systems, vol. 2, no. 1, May

1984.

F.Baccelli and M.Canales, 1993. Parallel Simulation of

Stochastic Petri Nets Using Recursive Equations,

ACM Trans. Machines and Computer Systems, vol. 3,

pp. 20-41, 1993.

Salimifard K, Wright M, 2001. Petri net-based modelling

of workflow systems: an overview. European Journal

of Operational Research, 2001,134(3):664~676.

F.P.Kelly, R.J.Williams, 2004. Fluid model for a network

operating under a fair bandwidth-sharing policy. The

Annals of Applied Probability, 2004, Vol.14, No.3,

1055-1083.

Law, Averill M., and Kelton, David W, 1991. Simulation

Modelling & Analysis. McGraw Hill.

ICEIS 2005 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION