
FACIAL POLYGONAL PROJECTION
A new feature extracting method to help in neural face detection
Adriano Martins Moutinho, Antonio Carlos Gay Thomé
Núcleo de computação eletrônica, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brasil
Pedro Henrique Gouvêa Coelho
Faculdade de Engenharia, Universidade do Estado do Rio de Janeiro, Rio de Janeiro, Brasil.
Keywords: Face detection, polygonal projection, neural network, image processing.
Abstract: Locating the position of a human face in a photograph is likely to be a very complex task, requiring several
image and
signal processing techniques. This paper proposes a new approach called polygonal facial
projection that is able, by measuring specific distances on the image, to extract relevant features and
improve efficiency of neural face identification systems (Rowley, 1999) (Moutinho and Thomé, 2004),
facilitating the separation of facial patterns from other objects present in the image.
1 INTRODUCTION
In order to successfully recognize and identify a
human face, it is first necessary to find the position
of the face in a wider scenario, where other objects
and a complex background are oftenly present.
(Rowley, 1999) and (Moutinho and Thomé,
2
004) proposed neural face identification systems
that employed neural network and several image
preprocessing techniques.
In the aforementioned works, artificial neu
ral
networks (ANN) (Haykin, 1994) were fed with
luminance values of a grayscale image. Based on
these values the ANN could decide if the image
constituted a human face or not.
However, articles such as (Vianna and
Ro
drigues, 2000) show that it is possible to improve
neural network recognition capabilities by extracting
specific image features, instead of simply using
luminance values directly as ANN input.
This paper proposes a modification in the neural
net
work detection schemes proposed in (Rowley,
1999) and (Moutinho and Thomé, 2004), by
introducing a new technique to extract image
characteristics – the polygonal projection.
The polygonal projection used in this paper is an
adapt
ation of the method proposed in (Vianna and
Rodrigues, 2000) to aid in face identification. It is
based on the measurement of distances between the
image limits and specific singular points.
The adaptation of polygonal projection presented
here
can be used in other pattern identification
problems using neural networks. It is adequate to be
used in any grayscale images, not only on binary
black and white images as the original technique and
other projection methods.
Section 3 describes the polygonal projection
m
ethod and section 4 shows results and conclusions.
More details about the face detection system can
be f
ound in (Moutinho and Thomé, 2004), polygonal
projection described in this paper improves its
capability.
2 FACE DETECTION SYSTEM
The face detection system can be divided in four
stages, as shown in figure 1.
The windowing process splits the original figure
i
n several squared subimages. Every subimage is
considered a face candidate.
The preprocessing and encoding phase is a
co
llection of processes applied in order to adapt the
original image to a neural network input. Polygonal
projection is one of these processes.
The neural network phase represents a Multi
Layer Pe
rceptron (MLP) previously trained to detect
facial patterns, and the last phase performs a fine
adjustment in face position. More details about the
face identification system can be found in (Moutinho
and Thomé, 2004).
419
Martins Moutinho A., Carlos Gay Thomé A. and Henrique Gouvêa Coelho P. (2005).
FACIAL POLYGONAL PROJECTION - A new feature extracting method to help in neural face detection.
In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 419-422
DOI: 10.5220/0002539404190422
Copyright
c
SciTePress

Figure 1: Face detection system
3 POLIGONAL PROJECTION
When a neural network is used in image pattern
recognition, it is necessary to extract features from
the images to feed the neural network.
Although the bitmap is often used as features to a
neural network, sometimes it may not be adequate.
Changes in size, position or rotation in the image are
likely to change most values in the bitmap, but are
unlikely to change the class of the image.
If, for example, a face image is slightly shifted to
the left, most features extracted from bitmap values
will probably change. However, that will not change
the fact that it is a face. The neural network will
have to generalize these differences in order to
achieve good results.
This paper proposes a method of feature
extraction to help in image size and position
normalization. It was previously used in (Vianna and
Rodrigues, 2000) and it is called polygonal face
projection. In (Vianna and Rodrigues, 2000), a black
and white handwritten character is placed inside of a
polygon. Then, distances between the polygon’s
sides and the first black pixel in the character are
computed. A set of these distances is used to
represent the character to the neural network. This
method, called polygonal character projection,
improves generalization in neural network character
recognition (Vianna and Rodrigues, 2000).
However, it is not possible to apply the
polygonal projection proposed in (Vianna and
Rodrigues, 2000) in neural face detection. Faces are
grayscale images, and changing it to black and white
will probably cause the loss of relevant information.
This paper proposes an adaptation on the
polygonal character projection method to allow its
use in a grayscale image, where there is no simple
method to measure the distances between the first
black pixel and the polygon’s side. A concept of
projection energy is created.
Projection energy is a number, previously
defined, that will be subtracted from image
luminance values in a certain projection direction.
Let figure 2 defines a projection direction; the
energy value will be subtracted by luminance pixels
values in the direction of arrow in figure 2.
Figure 2: Projection direction in a face.
Thus, from the border of the image in figure 2,
energy will be subtracted by luminance pixels in the
projection direction. When the luminance of a new
pixel is subtracted and the resultant energy becomes
zero or less, a distance between the initial point and
the zero point is computed, this is the projection
distance and it is considered a feature extracted from
the original face.
Polygonal projection with energy concept is
related to x-ray feature extraction used in medicine.
In this case, an x-ray emitter will sensibilize a
special film according to blocking characteristics in
the objects. Bones, for example, usually block x-ray
emission, making the film white.
In a polygonal face projection, higher values of
luminance will block projection and result in lower
distance values. On the other hand, if only lower
luminance pixels are found in the projection
direction, the distance extracted will be higher.
In the case of face detection, inverting the image
before extracting distances using polygonal
projection could lead to better results. As a result of
image inversion, black areas will block projection
and white areas will not.
The motivation for the inversion of the image
can be seen in figure 2. The eyes’ position is likely
to be darker than the rest of face image, which
facilitates their detection, since it will probably
block projection. The mouth and nose area also
likely to be darker than the rest of the face image.
Image inversion will make face features such as
eyes, mouth and nose to be detected by polygonal
projection, because it will block projection.
Detecting eyes, mouth and nose position is an
important step to successfully detect a face.
Another adaptation in the polygonal projection
method is to square every element in the original
image before projection. Squaring elements will
reduce very much the values in the range between 0
and 0.5, and will prevent that sequences of lower
luminance values reduce energy. Only values higher
than 0.5 will continue to block projection.
Squaring elements in the original image is also
related to the way x-ray emission is exponentially
attenuated by objects (Jain, 1989).
As in (Vianna and Rodrigues, 2000), choosing
the polygon defines all projection directions. In this
paper, a square will be used as the base polygon;
distances will then be extracted orthogonally to the
square sides, as show in figure 3.
ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
420
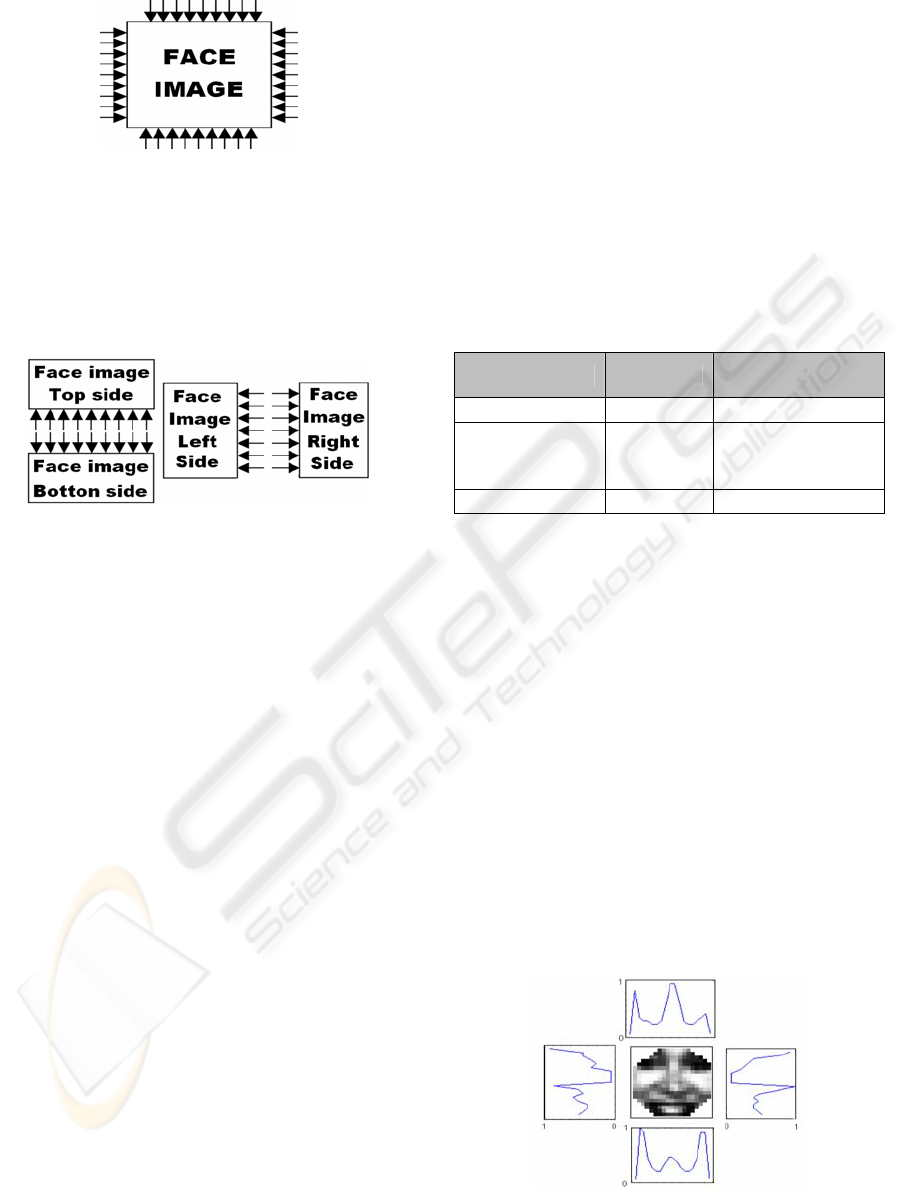
Figure 3: Projection directions using a square as the base
polygon
However, face images are likely to have
information in the picture center that is relevant to
classification. In order to avoid loosing central
information the image is divided in two parts
horizontally and two parts vertically, so it’s possible
to extract projections again, as described in figure 4.
Figure 4: Directions of polygonal projection dividing
an image in four parts
Since projections are extracted line by line or
column by column over the image, an HxV sized
image will have a number of features equal to:
VHN
ojections
⋅+⋅
=
44
Pr
The number of features extracted in image
defines the size of the neural network (Haykin,
1994). It’s important to reduce data size to have fast
training and processing methods. In a square image
where
, polygonal projection will extract less
features than bitmap considering images bigger than
8x8. The database used in this paper, shown in
figure 3, is 19x19 sized. The number of extracted
features will be 152 and the number of values in the
luminance matrix will be 361.
VH =
Although the number of features extracted will
be higher using bitmap, it’s possible to show that
polygonal projection features are more relevant to
classification because generalization is improved, as
will be shown in section 4.
Principal Components Analysis (PCA) suggests
that polygonal extraction conveys more information
than bitmap. PCA projects data in a new space
where new variables are statistically uncorrelated
(Zurada, 1999) (Haykin, 1994). By using PCA it’s
possible to reduce the size of training data by
removing low variance variables of the new data
space, keeping most of the original relevant
information.
Table 1 shows PCA application in a database of
face images containing 5000 examples. First PCA is
applied in the database using bitmap features, then in
a database using polygonal projection. In both cases
the database is normalized to have zero mean and
unitary variance (Zurada, 1999) (Haykin, 1994).
Using bitmap features, PCA projection can
reduce the number of variables from 361 to 58,
keeping 99% of relevant information. That shows
bitmap representation conveys too much irrelevant
information.
On the other hand, PCA application does not
reduce very much the number of variables using
polygonal features. That means polygonal projection
is able to keep more information, and might result in
fast training and better generalization.
Table 1: PCA application in database
PCA tests Bitmap
Poligonal
Projection
Original Size 361 152
Size using PCA
with 1% lost
information
58 126
Reduction % 83,9% 19,2%
Figures 9 and 10 show an example of polygonal
projection using initial projection energy equal to
“1”. White pixels in the image will let the projection
pass and black pixels will block projection. The face
image in figures 9 and 10 are not shown inverted or
with squared elements, but projections are taken
using these modifications. In figure 5a, the first four
sets of projections is taken. Each plot has 19 points
that indicate each projection distance. Figure 5b
shows the projections taken by splitting the original
face horizontally and vertically.
In figure 6a and 6b, the same polygonal distances
are extracted from a non-face figure. It’s possible to
compare projections from face and non-faces images
and observe that figures 9a and 9b show face
characteristics such as symmetry, position of eyes
and mouth. On the other hand, there is no symmetry
in the plots of figures 10a and 10b, facilitating face
patterns identification.
Figure 5a: Example of polygonal projection in a face
image. First set of four projections
FACIAL POLYGONAL PROJECTION - A new feature extracting method to help in neural face detection
421

Figure 5b: Example of polygonal projection splitting the
face image horizontal and vertically
Figure 6a: Example of polygonal projection in a non-face
image. First set of four projections
Figure 6b: Example of polygonal projection splitting the
non-face image horizontal and vertically
4 RESULTS AND CONCLUSION
To compare the performance of the polygonal
projection proposed in this paper, against the bitmap
feature extraction, a set of thirty-two neural network
architectures were used by changing the number of
hidden layers and activation functions (Haykin,
1994). Every neural network used was trained using
Backpropagation with adaptive learning rate and
momentum (Haykin, 1994).
Table 2 shows the mean results of the 32 neural
networks using test database. This database is not
used to adjust weights during neural network
training.
According to table 2, the use of polygonal
projection improves the correct face recognition rate
by approximately 18%, showing that the method is
capable of extracting features that are relevant to
classification, improving generalization.
Table 2: Mean results of 32 different ANN
Correct Recognition Rate
Results
Faces Non-faces
Bitmap 47,97% 96,83%
Polygonal
Projection
65,84% 92,07%
% Gain of 17,87% Loss of 4,76%
However, correct non-face recognition rate
decreases about 5% using the new method, but this
small reduction should not be considered a problem.
The face detection system proposed can eliminate
elements wrongly recognized as faces (Moutinho
and Thomé, 2004).
As results in table 2 shows, polygonal projection
improves face detection with a small reduction in
non-face rejection. As the database used in this test
contains rotated faces and faces with eyes in
different positions, it’s possible to conclude that
polygonal projection provides some normalization in
these non standard faces, increasing neural network
generalization.
REFERENCES
Rowley, A. Henry; Kanade 1999, Takeo. Neural network-
based face detection. ISBN 0-599-52020-5, 1999.
Moutinho, A. M.; Thomé, A. C. G.; Biondi, L. B. C.;
Coelho H. G.; Meza L. A., 2004. Face pattern
detection. Congress and author’s name removed for
blind evaluation purposes.
Haykin, Simon, 1994. Neural Networks: A
Comprehensive Foundation, Prentice Hall PTR, ISBN
0023527617.
Jain, A. K., 1989. Fundamentals of digital image
processing, Prentice-Hall Inc. ISBN 0-13-336165-9.
Gonzalez, Rafael C.; Woods, Richard E.; Digital Image
Processing, 1992. Addison-Wesley Longman
Publishing Co., Inc. ISBN 0201508036.
Zurada, J. M., 1999. Introduction to Artificial Neural
Systems. PWS Publishing Co., ISBN 053495460X.
Viana K. G.; Rodrigues J. R.; YYY, C. G. A., 2000.
Extração de Características para o Reconhecimento de
Dígitos. Congress and author’s name removed for
blind evaluation purposes.
ICEIS 2005 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
422
