Public-Key Encryption Based on Matrix
Diagonalization Problem
Jiande Zheng
Department of Computer Science, Xiamen University, Xiamen 361005, P. R. China
Abstract. A research on the development of a new public-key encryption
scheme
based on matrix diagonalization problem over a ring of algebraic
integers is reported in this paper. The research is original, although it is still
in its early stage. The new public key encryption algorithm has three
original features that distinguish it from existing ones: (a) it works on an
infinite field instead of a Galois field; (b)it recognizes the ability of
adversaries to factor big integers; (c) it requires only simple (without
modulus) additions and multiplications for message encryption and
decryption, no high-order exponentiation is required.
1 Introduction
The idea of inventing new public key cryptographies by exploring the matrix
diagonalization problem (MDP) was first suggested in [1]. The original
encryption system was implemented with modulo-p addition and multiplications,
where p is a big prime, which was broken due to the fact that the characteristic
polynomial of the public key matrix can be factored efficiently over GF(p) using
Cantor-Zassenhaus algorithm [2]. Improved public key encryption and digital
signature schemes were developed later with the same idea, but with the
underlying algebraic setting selected differently as Zn, the ring of integers with
modulo-n addition and multiplication, where n is an RSA modulus [3][4]. The
new selection links MDP to integer factorization problem (IFP). In fact,
diagonalizing a 2×2 matrix over Zn is equivalent to solving a modulo-n quadratic
equation, or inverting the Rabin public key function [5], which is a proven hard
problem.
The purpose of this paper is to report the further research on developing an
encry
p
tion scheme based on MDP over yet another algebraic setting, which is an
infinite field instead of a Galois field, as is the case with almost all existing
schemes. Since factoring a polynomial over the specially formulated algebraic
setting is a brand new crypto problem, the complexity of which is still under
study. However, we have made important progress on this aspect, which will be
presented in this paper.
Zheng J. (2005).
Public-Key Encryption Based on Matrix Diagonalization Problem.
In Proceedings of the 3rd International Workshop on Security in Information Systems, pages 102-112
DOI: 10.5220/0002543101020112
Copyright
c
 SciTePress

2 The new encryption scheme
2.1 The algebraic setting
First, we choose a big composite integer, denoted n, which is a product of a large
number of primes. Let p and q be two secret divisors of n, pq=n, a ring of
algebraic integers, denoted Ω, can be defined as
},,2,:{
21212
2
2
2
1121
]s[RqpnΩ ∈=+=+= ααααωααωωω
(1)
where
},:)({
32121
1
3
*
Zz,ZzzszzzR ∈±∈+=
−
,]s[
(2)
s is an integer,
s
is an irrational number, Z stands for the ring of integers,
...}.,3,2,1{
...},,3,2,1,0{
=
±
±±=
±
*
Z
Z
Another algebraic setting, denoted Π, can be defined with Ω,
},,{
2121
]n,s[R ∈∈+= πΩπππΠ
(3)
where
}:{
2121
]s[,]n,s[ RrrnrrR ∈+=
(4)
It is easily verified that
]n,s[R
is a field under normal addition and
multiplication. Meanwhile, one notices that (1) can be rewritten as
},:{
2121
]s[RqpΩ ∈+= αααα
(5)
for any
,
,
21
21
Ω∈+=
Ω∈+=
qvpvv
qupuu
103

]n,s[R ∈+= nwww
21
,
one obtains
],,[)()(
))((
))((
12212211
2121
2121
nsnvuvuqvupvu
qupuqvpvvu
qvpvqupuuv
R∈+++=
++==
++=
and
.)(
)(
)(
)(
2121
2121
21
21
21
Ω ∈++=
++=
+=
+==
+=
pquqpuwuw
qupupqwuw
nuwuw
unwwwu
nwwuuw
One notices from the above discussions that Π is closed under ordinary addition and
multiplication. Further more, let
Π
ξ
ξ
ξ
∈
+
=
21
, where
]ns[ ,,
21
RΩ ∈∈ ξξ
,
one also obtains from the above discussion
]ns[ ,,
2
2
2
1
R∈ ξξ
,
and
]ns[ ,))((
2
2
2
12121
R∈−=−+ ξξξξξξ
,
which is invertible within
]ns[ ,R
, and
]ns[ ,)()(
21
12
2
2
1
R∈−−
−
ξξξξ
gives the inverse of
21
ξ
ξ
ξ
+=
in
Π
. So we conclude that Π is also a field under
normal addition and multiplication.
There are 168 primes between 1 and 1000[6], we suggest that n be selected as 150
primes among them, so that
, the size of which will be
comparable with that of widely used RSA modulus[7].
1500450150
210)1000( <=<n
104

2.2 The keys
The private key for the encryption scheme is given by
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
−−−−−
−−−−−
1...1111
...
...
..................
...
...
4321
22
4
2
3
2
2
2
1
22
4
2
3
2
2
2
1
11
4
1
3
1
2
1
1
r
r
r
r
rrrr
r
r
rrrr
λλλλλ
λλλλλ
λλλλλ
λλλλλ
H
(6)
where
,},,,,,,,
,)(
)({...,,
424132312221121
42413231
2221121121
Πωωωωωωωω
ωωωω
ωωωωλλλ
⊂∈
++++
++++∈
Z
nss
nss
r
r>4, while the public key is given by
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−−−
=
−
1
1
1
1
1
)1(...
1
4321 r
r
σσσσσ
A
(7)
where σ
1
, σ
2
, …σ
r
are algebraic integers computed from λ
1
, λ
2
,… λ
r
using the
following equations:
....
......
...,
,
,
1321
111
3
11
2
1
1
rrr
r
i
k
r
ij
j
r
jk
i
r
i
j
r
ij
i
r
i
i
λλλλλσ
λλλσ
λλσ
λσ
−
=+=+=
=+=
=
=
=
=
=
∑∑∑
∑∑
∑
105

We have [8]
)(mod)...,,(
1
21
ndiag
r
−
= HHA λλλ
(8)
Note that the private key can be represented by (λ
1
, λ
2
,…λ
r
), while the public key
can be represented by (σ
1
, σ
2
, …σ
r
).
2.3 The trap-door one-way function
The following trap-door one-way function is used for message encryption in this
paper:
Π ∈+++=
−−
rr
rr
r
xxxxxxxxxf ,...,,)...(),...,(
21
22
2
1
121
bIAA
(9)
where
is an r×1 matrix, the elements of which can be
computed as
, so that
[
T
r
bbb ...
21
=b ]
ritrb
ir
i
...,2,1),( ==
−
A
[
]
T
1...11Hb =
(10)
2.4 Message encryption
The encrypting process is divided into the following three steps
Step 1 Create r random numbers in
Ω. These numbers, denoted , can be
computed from the public key as
r
xxx ,...,
21
,1...,3,2,)...(
,)...(
12211
16
2111
−=++=
++=
−
rixkkkx
kx
iiii
r
σσσ
σσσ
(11)
and
)...,,(
1211 −
=
rr
xxxx
ψ
(12)
106

where
are random numbers in
r
kkk ,...,
21
]s[ R
,
1
ψ
is a publicly known
one-way function, which can be made as the combination of a hash function with
some arithmetic operations.
Step 2 Compute the first component of the cipher-text, denoted y, which is an r×1
matrix obtainable from the public key function:
bIAAy
22
2
1
1
)...(
r
rr
xxx +++=
−−
(13)
Step 3 Compute the second component of the cipher-text, denoted z, which is an
integer,
)...,,(
212 r
xxxmz
ψ
=
(14)
where m is the message,
2
ψ
is a publicly known one-way function similar to
1
ψ
.
The full cipher text of m is given by (y, z).
2.5 Message decryption
One notices that (13) can be reduced to a univariate quadratic equation by multiplying
the inverse of H on both sides of the equation. We have
,)...)()([
)...(
1221
2
11
1
122
2
1
1
11
bHIAHHAHH
bHHIAAHyH
−−−−−
−−−−−
+++=
+++=
r
rr
r
rr
xxx
xxx
(15)
where
)...,,()(mod
21
1
r
diagn λλλ =
−
AHH
,
which is an alternative form of (8). Let
[
]
T
r
δδδ ...
21
1
=
−
yH
,
rixxx
r
r
i
r
ii
,...2,1,...
2
2
1
1
=+++=
−−
λλµ
(16)
where
, and equation (15) can be reduced to [
T
r
xxx ...
21
=x ]
107

[]
[
]
[]
,...
1...11)...,,(...
22
2
2
1
22
2
2
121
T
r
T
r
T
r
diag
µµµ
µµµδδδ
=
=
which can be further rewritten as
ri
ii
,...2,1,
2
== µδ
(17)
The above equations are readily solved, the solutions of which are given by
ri
ii
,...2,1, =±= δµ
(18)
Meanwhile, one obtains from (6) and (16)
[
]
Hx
T
r
= µµµ ...
21
,
so we have
[
]
1
21
...
−
= Hx
r
T
µµµ
(19)
Note that 2
r
possible solutions to (13) can be computed from (18) and (19), and
(12) can be used to find out the correct one. The original message can then be
recovered as
1
212
)]...,,([
−
=
r
xxxzm ψ
.
3 Security of the encryption scheme
We study in this section two kinds of possible attacks on our encryption scheme. The
first kind of attacks aims at recovering the secret key, while the second kind of attacks
tries to crack the cipher texts.
3.1 Attacks aiming at recovering the private key
An adversary can recover H, if and only if the adversary can diagonalize the
corresponding public key A, or factoring its characteristic polynomial
108

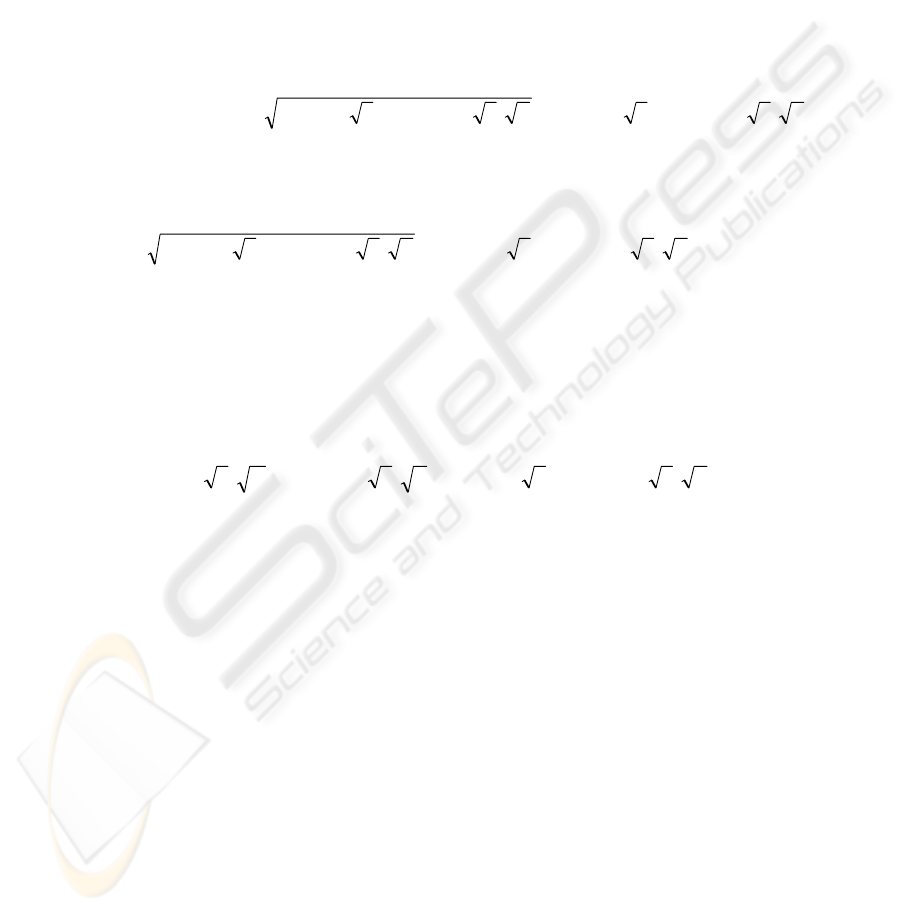
r
rrrr
σλσλσλλλφ )1(...)det()(
2
2
1
1
−++−=−=
−−
AI
(20)
over Π. Since Π is an infinite field, the polynomial factoring algorithms that work
well on Galois fields, such as the famous Cantor-Zassenhaus algorithm, will not work
on it. According to Abel’s theorem [9], it is also hard for the adversary to solve
φ(λ)=0 over R, the real number field, as this task is incapable of finite number of
additions, multiplications and root extractions if r>4.
The adversary may also substitute
nssnss )()(
4241323122211211
ωωωωωωωωλ +++++++=
into (20) and transform φ(λ)=0 over Π to
,Z
nssnss
∈=
+++++++=
424132312221121
4241323122211211
424132312221121
,,,,,,,,0
))()((
),,,,,,,(
ωωωωωωωω
ωωωωωωωωφ
ω
ω
ω
ω
ω
ω
ω
ω
ψ
(21)
However, it is easily verified that (21) can not be broken into a small number of
rational equations over Z, so this transformation can not reduce the complexity of
recovering the private key.
The third method for key recovery is substituting
Z
nssqsps
∈
+++++++=
4241323122211211
4241323122211211
,,,,,,,
,)()()(
ωωωωαααα
ωωωωααααλ
into (20), which will transform φ(λ)=0 over Π to eight polynomial equations of
4241323122211211
,,,,,,, ωωωωαααα
over Z. This transformation makes it possible to recover the private key with existing
polynomial factorization algorithms over finite fields. However p and q, the factors of
n, should be found before the above method can be applied, and for this purpose we
can not find any existing method that is more effective than enumeration. Suppose n
is selected as a product of 150 different primes, and p is selected as the product of 70
prime factors of n, it takes maximal
tries for the adversary to find p. We have
70
150
C
1294370
150
21066.6 >×=C
,
109

which is more than the number of all 128-bits symmetric keys.
3.2 Attacks aiming at cracking the cipher texts
We have studies three methods that may be used to solve (20). These methods may
also be used to solve (13), in order to crack the cipher text directly. Complexity of
applying the second and the third methods to (13) is the same as that of applying it to
(20), while complexity of solving (13) over R depends heavily on that of reducing it
into quartic or lower order univariate equations. The basic methods for the reduction
are linear transformations, including linear eliminations and linear substitutions. We
have the following proposition:
Proposition 1 Breaking (13) into univariate equations through linear
transformations is as hard as finding the eigenvalues of A.
Proof One may represent a scalar equation obtained from (13) through linear
eliminations as
bIAAvyv
22
2
1
1
)...(
r
rrTT
xxx +++=
−−
,
where v is an r×1 matrix. Suppose the above equation can be turned into a univariate
equation through linear substitution, there exist three scalars
321
,,
γ
γ
γ
and an
r×1matrix u, so that
satisfies
xu
T
= ε
32
2
1
22
2
1
1
)...( γεγεγ ++≡−+++
−−
yvbIAAv
T
r
rrT
xxx
(22)
According to (8) and (10), the left side of (22) can be rewritten as
[]
,...
...
)...,,(
)...(
0
22
22
2
11
2
2
2
2
2
1
122
2
2
1
22
2
1
1
wwww
diag
xxx
rr
T
T
T
T
r
T
T
r
rrT
−+++=
−=
−=
−+++
−
−−
µµµ
µµµ
µµµ
yvw
yvbHHv
yvbIAAv
(23)
110

where
, ,
yv
T
w =
0
[]
Hvw
TT
r
www ==...
21
0≠w
since H is of full
rank. Without loss of generality, we assume that
0
1
≠
w
. Meanwhile one obtains from
(19)
[]
,......)(
221121
1
rr
T
r
TTT
ddd µµµµµµε +++===
−
Huxu
(24)
where
[
. Substituting (23) and (24) into (22) gives
]
uH
1
21
...
−
=
T
r
ddd
322112
2
22111
0
22
22
2
11
)...()...(
...
γµµµγµµµγ
µµµ
++++++++≡
−+++
rrrr
rr
dddddd
wwww
(25)
and one obtains from the above equation
0......,
3232
2
111
=======
rr
dddwwwdw γ
.
So we have
[]
[
]
0...0...
121
wwww
r
T
==Hv
(26)
which reveals the fact that v is a left eigenvector of A, and an eigenvalue of A can be
obtained by multiplying A with it on the left side.
In summary, obtaining a univariate equation from (13) through linear
transformations is equivalent to computing an eigenvalue of A. If an adversary can
obtain r independent univariate equations from (13), the adversary will also be able to
obtain all r eigenvalues of the public key matrix. This is the end of the proof.
4 Conclusions
Extracting irrational roots from a high-order polynomial equation has been proved to
be an impossible task, while complexity of finding a secret composite factor from a
big integer is decided by the number of prime factors contained in the integer, and
apparently irreducible with algebraic tools. Our encryption scheme is novel since we
have built a strong relationship between complexity of breaking the scheme to that of
111

solving the above two original problems, which are different substantially from the
underlying mathematical problems of existing public-key encryption schemes.
However we have not been able to reduce the cryptographic problem formulated in
this paper to either of the proven hard problems mentioned above. The security topics
that remained open to further research includes the complexity of reducing (13) to
quartic or lower order univariate equations through nonlinear transformations and the
complexity of solving (13) over R without breaking it into univariate equations.
Acknowledgements
This research is supported by National Natural Science Foundation of China under
Grant 60373077.
References
1. J. D. Zheng, “A new public key cryptosystem for constrained hardware”, in LNCS
2433, New York: Springer-Verlag, 2002, 334-341
2. D. Cantor, and H. Zassenhaus, “A new algorithm for factoring polynomials over finite
fields”, Math. Comp., 1981, 36: 587-592.
3. J. D. Zheng, “An Economical public-key crypto-device for C/S and B/S
applications”, Journal of Xiamen University, 2004, vol. 43(2): 141-143
4. J. D. Zheng “A fast digital signature scheme based on MDP”, Journal of Computer
Research and Development, 2005, 42(2) to appear
5. M O Rabin, Digital signatures and public key functions as intractable as factorization.
MIT Laboratory for Computer Science, Technical Report: MIT/LCS/TR-212, 1979
6.
http://www.utm.edu/research/primes/howmany.html
7. B. Schneier, Applied Cryptography, New York: John Wiley & Sons, 1996
8. T. W, Hungerford, Algebra, New York: Springer-Verlag, 1974, pp. 114-145
9. Raymond G. Ayoub, On the nonsolvability of the general polynomial, American
Mathematical Monthly 89(1982), 397-401
112