A NEW PUBLIC-KEY ENCRYPTION SCHEME BASED ON
NEURAL NETWORKS AND ITS SECURITY ANALYSIS
Niansheng Liu
College of Computer Engineering, Jimei University, Xiamen 361021, China
Donghui Guo
Department of
Physics, Xiamen University, Xiamen 361021, China
Keywords: Neural networks, Public-key cryptosystem
, Chaotic attractor, Matrix decomposition.
Abstract: A new public-key Encryption scheme based on chaotic attractors o
f neural networks is described in the paper.
There is a one-way function relationship between the chaotic attractors and their initial states in an
Overstoraged Hopfield Neural Networks (OHNN), and each attractor and its corresponding domain of
attraction are changed with permutation operations on the neural synaptic matrix. If the neural synaptic matrix
is changed by commutative random permutation matrix, we propose a new cryptography technique according
to Diffie-Hellman public-key cryptosystem. By keeping the random permutation operation of the neural
synaptic matrix as the secret key, and the neural synaptic matrix after permutation as public-key, we introduce
a new encryption scheme for a public-key cryptosystem. Security of the new scheme is discussed.
1 INTRODUCTION
Networking security is one of key problems in the
study of IPng (Goncalves, 2000), and the encryption
algorithm selected for IPSec is the core of this key
problem. In order to meet the requirements of
multimedia real time communications via the IPng,
the encryption algorithm should have higher
complexity for the security of information system,
and higher processing speed for the efficiency of
information encryption and decryption. So, neural
networks, with the properties of nonlinear dynamics
such as chaotic behavior and parallel processing, are
regarded as one of good design options for encryption
algorithm applied in the communications of IPng.
Since the thought of public-key cryptosystem was
pr
oposed (Diffie, 1976), the public-key scheme has
been the focus of modern cryptographist’s attention.
Many algorithms of public-key encryption were put
forward in recent years (Stallings, 2003). However,
the encryption scheme of public-key based on neural
networks isn’t reported till now.
Although neural networks are made up of simple
ele
ments, they have complex nonlinear dynamics
with chaotic attractors. Since the synchronization of
chaotic system was discovered (Pecora, 1990), some
symmetric encryption schemes base on the chaotic
synchronization of neural networks have been
proposed (Crounse, 1996, Milanovic, 1996, Donghui
1999). Here, we will introduce a new public-key
encryption scheme based on the chaotic attractors of
neural networks according to Diffie-Hellman
public-key cryptosystem and commutative matrix
theory.
2 PRINCIPLES OF THE
PROPOSED SCHEME
For a discrete HNN(Hopfield,1982), if system initial
state is converge to one of the system attractors by a
Minimum Hamming Distance (MHD) criterion, the
attractor is a stable state as an associative sample of
HNN and can be stored in HNN. If the number of
sample to be stored is over the capacity of HNN, the
stable attractors of HNN system will be became
aberrant and chaotic attractors will emerge. The
capacity of networks is increased. HNN becomes
overstoraged HNN (OHNN).
Guo Donghui and Chen L. M. further proved that
these attractors are cha
otic, and message in the
attraction domain of an attractor are unpredictable
related to each other. After the neural synaptic matrix
T multiplied by random permutation matrix H,
425
Liu N. and Guo D. (2005).
A NEW PUBLIC-KEY ENCRYPTION SCHEME BASED ON NEURAL NETWORKS AND ITS SECURITY ANALYSIS.
In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 425-428
DOI: 10.5220/0002545804250428
Copyright
c
 SciTePress

original initial state S and corresponding attractor
become new initial state Ŝ and attractor Ŝ
µ
S
µ
,
respectively. They are shown as follows:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+=+
∑
−
=
i
N
j
iji
tSTftS θ
1
0
)()1(
(1)
H
T
H
T
′
∗∗=
ˆ
(2)
HSS ∗=
µµ
ˆ
Where H
/
is the transpose of matrix of H.
Provided that neural synaptic matrix T is a
nn
×
singular matrix, and H is a
random
permutation matrix. For any given T and H,
Ť=H*T*H
nn ×
/
is easy to compute according to matrix
theory, and Ť is a singular matrix too. Furthermore,
there is a kind of special matrix, which is referred as
commutative matrix, in the random permutation
matrix (Chen, 2001). Suppose that H
1
and H
2
both are
two of commutative matrices, and they have same
order. Then, they must meet the following equation:
H
1
*H
2
=H
2
*H
1
According to Diffie-Hellman public-key
cryptosystem, all users in a group jointly select a
neural synaptic matrix T
0
, which is a singular
matrix. Each user randomly selects a permutation
matrix from a
commutative matrices group.
i.e., user A firstly selects any nonsingular matrix H
nn ×
nn ×
a
from this commutative matrices group, and compute
T
a
=H
a
*T
0
*H
/
a
. Secondly, he keeps T
a
open as a
public key, and keeps H
a
secret as a private key.
When user A and B in a group need secure
communication, they will get a shared key
T=H
a
*T
b
*H
/
a
=H
b
*T
a
*H
/
b
. User A or user B can
easily compute the shared key using his own private
key and the other’s public key. However, the third can
not obtain the shared key because it is
computationally infeasible to calculate the shared
secret key T given the two public values T
a
and T
b
when the number of neurons n is sufficiently large.
In order to improve the security of information
during network transmission, the authenticated
Diffie-Hellman key agreement protocol (
Emmanuel,
2001) is proposed to adopt in the new scheme. The
immunity is achieved by allowing the two parties to
authenticate themselves to each other by the use of
digital signatures and public-key certificate.
3 ENCRYPTION SCHEME
According to the properties of chaotic attractors in
OHNN, we know that a lot of chaotic-classified
attractors can be obtained as long as stored
sample
or a few of neural synaptic strength T
µ
S
ij
are
modified. So we can design a new public-key
encryption system with high security, as shown in
Fig.1. The encryption scheme can be described as
follows.
3.1 Key Generation and Distribution
As described in the previous section, all users in a
group needed secure communication jointly and
carefully select a neural synaptic matrix T
0
. The
synaptic matrix should meet the following
requirements: (1) it must be a singular matrix. (2)
Based on the statistical probability of MHD, if we
want to obtain more unpredictable attractors, the
neural network requires equal concentrations of
excitatory and inhibitory synapses (Gardner, 1987).
Suppose the actions between neuron i and neuron j
can be excitatory (T
ij
=1), inhibitory (T
ij
=-1), or not
direct connected (T
ij
=0). Thus, in each row and each
column of T
0
, the number of “1”, “-1” and “0” is
about equal. Then, the attractor set of T
0
is computed.
All users in a group randomly select a same coding
matrix M in common.
Each user in a group randomly selects a different
permutation matrix from a commutative matrix group.
i.e., user i randomly select a permutation matrix H
i
,
and keep it secret as a private key. Then, he computes
T
i
=H
i
*T
0
*H
/
i
and corresponding chaotic attractor set
of T
i
using Eq. (2), and keeps T
i
open as a public key.
Then, each user publishes his public key and
corresponding chaotic attractors by placing them in a
public register in the form of digital signatures and
gets a public-key certificate with authenticated
function from the public-key authority.
3.2 Encryption
The steps of data encryption are as follows:
(1) Shared key generation. The sender of
information firstly input his own private key H
s
and
accepts the public key T
r
and corresponding attractors
S
r
of T
r
, which are legal by authentication of digital
signatures, from an information receiver. Then, he
calculates the new neural synaptic matrix
T=H
s
*T
r
*H
/
s
and the attractors Ŝ of T using Eq. (2).
(2) Coding process. Use the coding matrix M and
attractor Ŝ
µ
belonging to T to map the plaintext Y onto
a coded plaintext Y
x
= {Ŝ
µ
}.
(3) Message generation. A random number of
forms {0, 1}
N
are generated by a pseudorandom
number generator (PRG) as the initial state S(0) for
the OHNN process based on synaptic matrix T. Using
Eqs. (1), a steady state
is obtained and
compared to the value of
. If =
µ
, a
message that belongs to the domain of attraction for
attractor Ŝ
)(∞S
µ
S
ˆ
)(∞S
S
ˆ
µ
is found, and the initial state S (0) is
outputted as the cipher text X for plaintext Y.
ICEIS 2005 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION
426

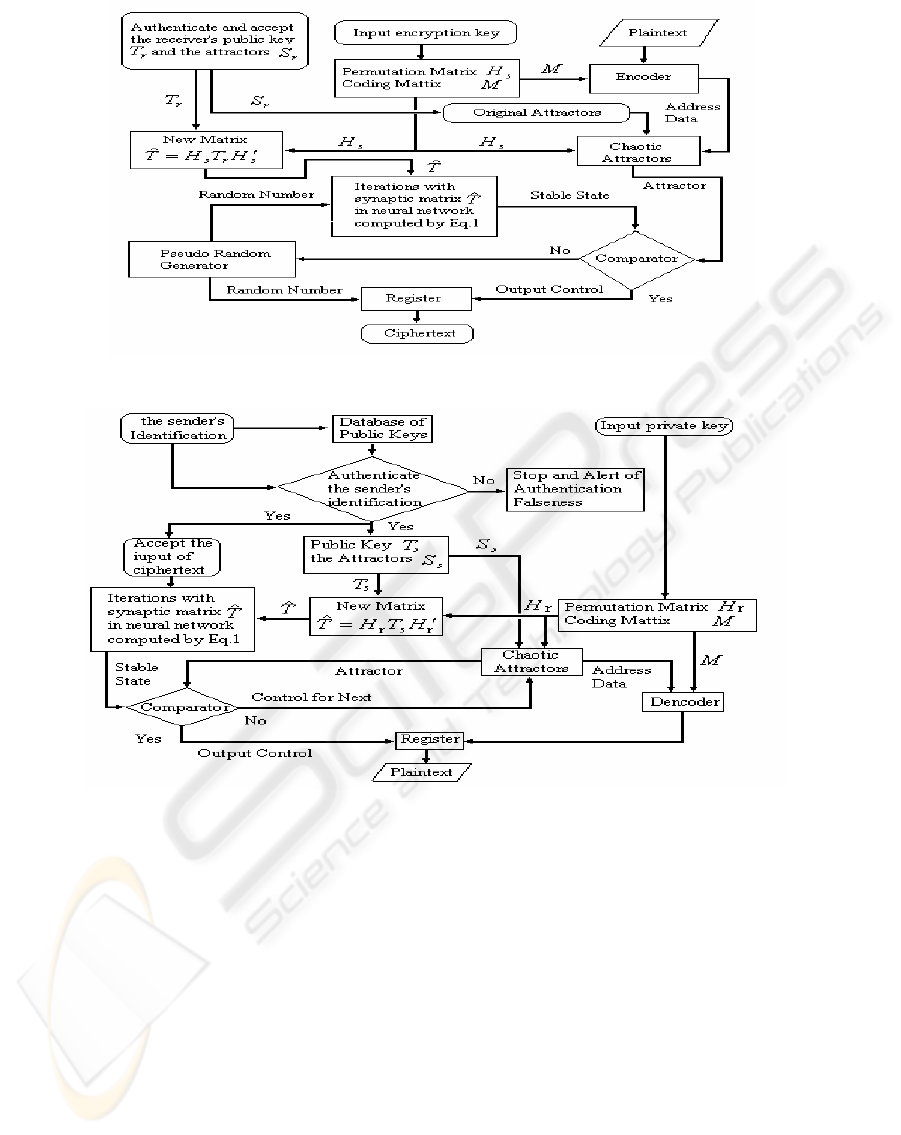
(a) Encryption scheme of the proposed cryptosystem
(b) Decryption scheme of the proposed cryptosystem
Figure 1: Diagram of the proposed cryptosystem
If Ŝ
≠∞)(S
µ
, PRG generate a new random
number as initial state S (0), and step as the previous
described is repeated.
3.3 Decryption
The steps of data decryption are as follows:
(1) Identification verification. The receiver firstly
verifies the identification of the sender based on his
public-key certificate. If the result of authentication is
true, the sender will be a legal user and the receiver
will accept the cipher text X. Otherwise, the receiver
rejects to accept any information coming from the
sender and gets an alert for authentication falseness.
(2) Decryption process. The receiver firstly inputs
his own private key H
r
, and accepts the public key T
s
and the attractor set Ŝ
s
of the sender. Calculate the
new matrix T=H
r
*T
s
*H
/
r
and new attractors Ŝ
µ
.
Secondly, inputs the cipher text X into Eq.(1) for
iterating, and the corresponding coded plaintext
Y
x
={Ŝ
µ
} is obtained. Finally, using coding matrix M,
decode Y
x
={Ŝ
µ
} into plaintext Y.
4 SECURITY
The security of the proposed cryptosystem is based on
the difficulty of singular matrix decomposition and
the chaotic-classified properties of OHNN. There are
two ways of finding the private key in the proposed
cryptosystem by attacking the chaotic properties of
OHNN or by matrix decomposition.
A NEW PUBLIC-KEY ENCRYPTION SCHEME BASED ON NEURAL NETWORKS AND ITS SECURITY
ANALYSIS
427

As stated in the previous section, the neural
synaptic matrix T
0
is a singular matrix. Thus, the
matrices T
s
, T
r
and T all are singular matrices. For any
given matrix T
0
, T
s
and T
r
, T is relatively easy to
compute according to matrix theory. However, for
any given higher order matrix T
s
, T
r
or T, it is
computationally infeasible to find permutation matrix
H
s
or H
r
. i.e. Only Hessenberg transform of matrix in
the method of conventional matrix decomposition can
succeed in finding permutation matrix. However, the
difficulty of computation can not be overcome.
Firstly, when any square matrix is transformed a
Hessenberg matrix, the complexity of computation
time is O (n
3
), where n is the order of T. Secondly, the
decomposition of Hessenberg matrix is not unique
(Chen, 2001). For any n order square matrix, the
number of Hessenberg decomposition is over 2
n
.
Thus, it is computationally infeasible to traverse the
space of Hessenberg matrices for any synaptic matrix
when n is larger.
As illustrated in the previous section, our
cryptosystem is designed based on the
chaotic-classified properties of the OHNN. It is
impossible to find the private key H by using
chosen-plaintext attack or known- plaintext attack at
present (Guo, 1999). Furthermore, the proposed
cryptosystem is uneven in the encryption and
decryption process, i.e. it uses a random substitution
during the encryption and auto-attraction during the
decryption. Differential cryptanalysis methods cannot
unfold our proposed cryptographic scheme because
of these uneven processes. Only an exhaustive search
based on the statistical probabilities of plaintext
characters can succeed in breaking our proposed
cryptosystem. However, the breaking cost of this
method is very high. i.e., for N =32, some 10
20
MIPS
years would be required for a successful search,
which is well above the acceptable security level of
current states, i.e., 10
12
MIPS years.
On the other hand, the necessity of our
cryptosystem is that the attractors are randomly
substituted by the messages in their domains of
attraction to eliminate the statistical likeness of the
plaintext and avoid this attack based on the statistical
probabilities of plaintext characters. So that, in the
encryption process, the number of messages in the
domain of attraction is another key parameter for the
security of our proposed cryptosystem. If the PRG for
random substitutions in our cryptosystem is designed
to have temporal variations, the same message in the
plaintext can be encrypted to different cipher texts at
different times. To break our proposed scheme using
probabilistic attacks requires that one store all the
information of the attractors and their domains of
attraction, which is not practical even when N is
reasonably large, i.e., N =32.
5 CONCLUSIONS
We propose a new public-key cryptosystem based on
the chaotic attractors of neural networks. According
to above discussions of the new cryptosystem, the
proposed scheme has a high security, and is
eminently practical in the context of modern
cryptology. Neural networks rich in nonlinear
complexities and parallel features are suitable for use
in cryptology to meet the requirement of secure
communication of IPng, as proposed here. However,
we do not know whether the new public-key
encryption scheme described in this paper can be kept
from new types of attack. The exploration into the
potential relevance of neural networks in
cryptography needs be studied in detail.
REFERENCES
Goncalves M., Niles K. 2000. IPv6 Networks. Beijing:
Post & Telecom Press, 41-334.
Haykin S., 2001. Neural Networks. Beijing:Tsinghua
University Press, 664-727.
Diffie W., Hellman M., 1976. New Directions in
Cryptography. IEEE Transactions on Information
Theory. 22(6):644—654.
Stallings W., 2003. Cryptography and Network Security:
Principles and Practice (2nd), Prentice Hall, Inc. 1-20.
Pecora L. M., Carroll T L. 1990. Synchronization in
Chaotic Systems. Physical Review Letters, 64(8):
821-824.
Crounse K. R., Yang T., Chua L. O., 1996. Pseudo-random
sequence generation using the CNN universal machine
with applications to cryptography. Proceedings of the
IEEE International Workshop on C NN and their
applications, 433-438.
Milanovic V., Mona E. Z., 1996. Synchronization of
chaotic neural networks for secure communications.
IEEE International Symposium on Circuits and Systems,
Circuits and Systems, 3, 28-31.
Guo Dong-hui, Cheng L. M., Cheng L. L., 1999. A New
Symmetric Probabilistic Encryption Scheme Based on
Chaotic Attractors of Neural Networks. Applied
Intelligence, 10, 71-84.
Hopfield J. J., 1982. Neural Networks and Physical
Systems with Emergent Collective Computational
Abilities. Proceedings of the National Academy of
Science, 79, 2554-2558.
Chen J. L., Chen X. H., 2001. Special Matrices.
Beijing:Tsinghua University Press, 309-382.
Gardner E., 1987. Maximum Storage Capacity in Neural
Networks. Europhys. Lett., 4, 481 - 485.
Emmanuel B, Olivier C, David P, et al. 2001. Provably
Authenticated Group Diffie-Hellman Key Exchange.
Proceedings of the ACM, 255-264.
ICEIS 2005 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION
428