A FORMAL LANGUAGE FOR MODEL TRANSFORMATION

SPECIFICATION

Dan Song, Keqing He, Peng Liang, and Wudong Liu

The State Key Laboratory of Software Engineering, Wuhan University 430072, China

Keywords: MDA, model transformation, meta-model, formal language

Abstract: Model transformation and its automation have been the core and major challenge of MDA; consequently

OMG issued a QVT RFP to standardize its process. Though many approaches have been proposed, their

efficiency cannot be validated and their application scope is still limited. The task of providing a reliable

solution to model transformation is critical. This paper proposes a formal language for model transformation

specification to achieve automatic implementation. The foundation of our work is explained and some basic

elements of the language are defined. A concrete transformation example from UML 1.4 models to UML

2.0 models is presented using the formalism.

1 INTRODUCTION

The Object Management Group (OMG)’s Model

Driven Architecture (MDA) (Joaquin Miller, Jishnu

Mukerji, 2003) initiative has gained widespread

reputation due to its adoption of a model-backboned

approach for software system development. The

process of building a final system can be regarded as

a series of model transformations. Model

transformation thus becomes the focus of model

driven software development (Shane Sendall,

Wojtek Kozaczynski, 2003).

A major challenge of the model-driven

development is to be able to achieve the automation

of model transformation. While there exist

well-established modelling standards, there lacks

sound model transformation mechanisms and hence

prevent it from automating. In order to change this

embarrassment, the OMG initiated a standardization

process by issuing a Request for Proposal (RFP) on

Query/Views/Transformations (QVT) in 2002 (Tata

Consultancy Services, 2003). As an effort to respond

to this RFP, a large number of approaches have been

proposed in the past two years (Krzysztof Czarnecki,

Simon Helsen, 2003). However, their effectiveness

cannot be guaranteed in practice. Additionally,

automatic tools available only offer limited

capabilities and lack proper theoretical foundation.

To achieve the maximum degree of automation,

we may need a precise and unambiguous modal

transformation language. A formal language, which

is mainly based on mathematical logic and set theory

can meet this goal. Formal language allows software

engineers to create integral, conformant and

unambiguous specifications. Additionally, formal

language is easy for automation.

In this paper, we present our effort to design

such a formal language for model transformation

specification. The paper is organized as follows.

Section 2 explains OMG’s transformation model,

which is our working foundation. Section 3 gives the

basic elements of our proposed formal language.

Section 4 presents a concrete example of model

transformation from the UML 1.4 model to UML

2.0 model. And Section 5 summaries our solution

and discuss the future work.

2 TRANSFORMATION MODEL

We introduce the OMG’s simplified QVT

transformation model (DSTC, IBM, CBOP, 2003),

shown in

Figure 1, to explain our working rationale.

As we can see from the figure, there are two types of

transformation: relation and mapping (Keith Daddy

et al., 2003). Relations are non-executable and can

-----------------------------------------------------------------------------

+This research project was supported by the National Natural

Science Foundation of China under Grant No. 60373086;

Wuhan Science & Technique Key Project under Grant No.

20021002043; Open Foundation of SKLSE under Grant No.

03-03; the Provincial Natural Science Foundation of Hubei

under Grant No. 2002ABB037; Hubei Province Key Project

under Grant No. 902130819.

429

Song D., He K., Liang P. and Liu W. (2005).

A FORMAL LANGUAGE FOR MODEL TRANSFORMATION SPECIFICATION.

In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 429-433

DOI: 10.5220/0002546104290433

 SciTePress

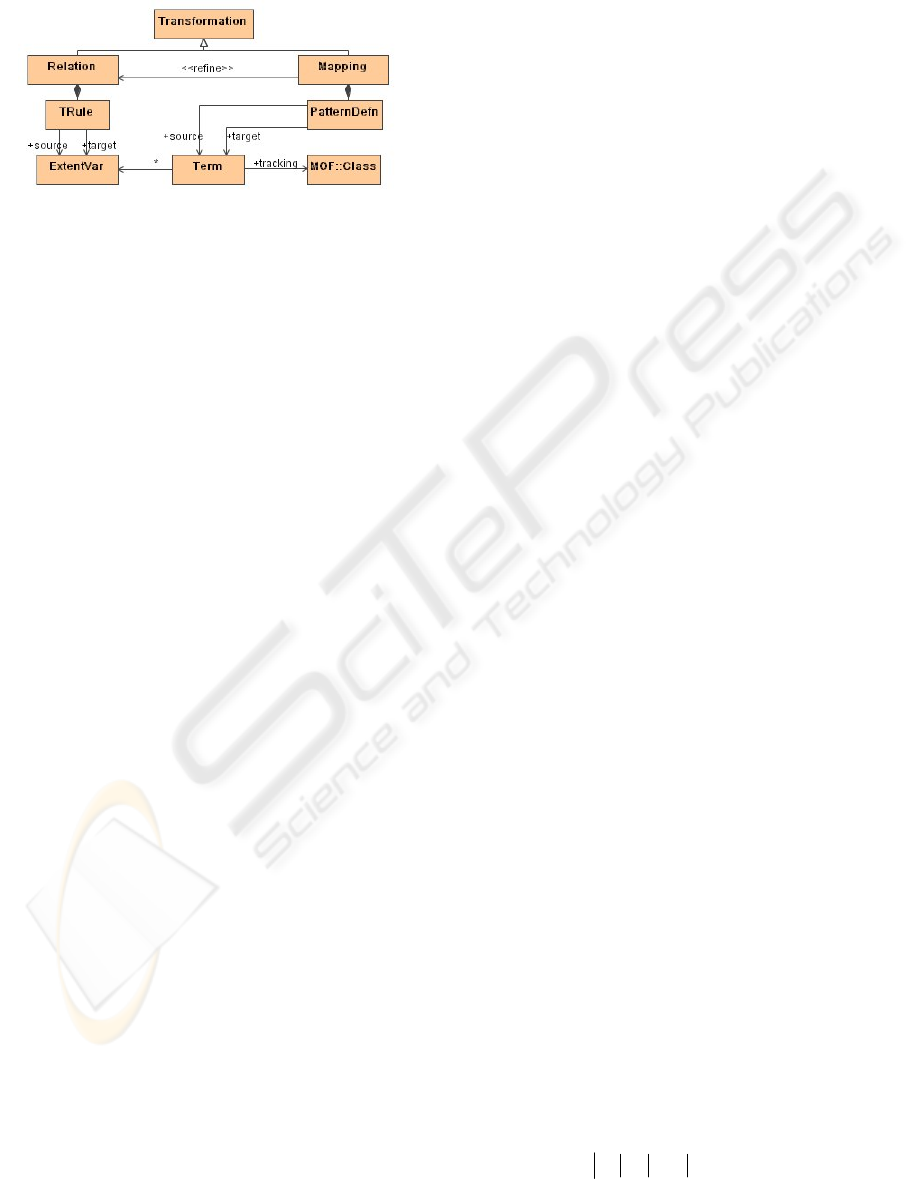
be automatically refined into mappings. Mappings

are typically uni-directional and must be consistent

with the relations it refines.

A model transformation specification defines how a

target model is derived from an existing source

model. Since MDA requires its model to be

well-formed, there are always two meta-models, i.e.,

source meta-model and target meta-model, to

validate their conformance. What will be

transformed are the actual data models, while rule

sets are defined on meta-model level. The

equivalence of source model and target model are

reflected in the static relations of the corresponding

meta-models.

On the lower level of Figure 1, we can see

clearly that the relation consists of several

transformation rules, represented by TRule. TRule is

usually responsible for transforming a clipping of

source model into a clipping of target model. So

each TRule has a source ExtentVar and a target

ExentVar. An ExtentVar is an extent variable

representing a meta-model or a meta-model

fragment, since a transformation rule. Similarly,

mapping is composed of several PatternDefn, which

is a pattern definition describing the details of

transformation. Each PatternDefn specifies how a

source Term is transformed into a target Term. And

a Term tracks to a MOF class in a model.

3 BASIC FORMALISM

As for the expression of specifications and

implementations of transformation, it may need a

specific modal transformation language. This

language should be precise and unambiguous. A

formal language based on mathematical logic and set

theory can meet this goal. Formal language allows

software engineers to create integral, conformant

and unambiguous specifications. Additionally,

formal language is easy for automation.

According to our designed transformation

model, such a formal transformation language

should provide at least definitions of three aspects:

- meta-model: a set of concepts to be matched

for an instantiated model,

- model: a set of entities to be dealt with by

transformation, and

- transformation: a functional mapping reflecting

a set of relations and evolution of elements from

the source to the target.

In the following, we will present the essential

formal definitions of all the elements in the

transformation model in part 2.

3.1 Definitions of Meta-models

ure 1: Transformation Model ada

ted from OMG.

These three consecutive concepts are defined on

meta-model level. To be mentioned here, all the

concepts have the most common sense. For example,

the attribute of class here is a general concept,

including universal attribute of the primitive type,

association end of Object type and method of the

class, and we use a full stop to attach it to its

belonging class. So a meta-model, which actually

contains meta-classes and associations between

them, can be simplified to be a group of

meta-classes.

Def1 A meta-class mc(id, A)

z An identifier id

z A meta-attribute set A of tuples (n, t) with

an identifier n and a type t, with the

property:

jijjjii ttnnAtntn i =⇒=

∈

∀

:),(),,(

Def2 A meta-model mm is a collection of

meta-classes {m

, m

,…,m

}, with the property:

:, mmmcmc ji

∈

∀

jiji mcmcidmcidmc =⇒

Def3 A meta-model fragment mmf(mm, MCC)

z A meta-model mm which it belongs to

z A set MCC is a collection of meta-classes,

with the property:

mmmmfMCCmmfmmf ..: ⊆

∀

3.2 Definitions of Models

Def4 to Def6 deals with the model and its containing

elements. These definitions are dependent on the

above definitions since models are the instances of

meta-models. So, each of the following definitions

attach a tag or mark reflecting its belonging meta

source.

Def4 A class c(id, mc, V)

z An identifier id

z A regarding meta-class mc

z An attribute set V of tuples (a, v), with the

property:

jijjjii vavaVvava i =⇒=

∈

∀

:),(),,(

,and

:.),(,.),(, AmctnVcvac ∈

∃

∈

∀

AmcVcna .. =∧=

, which ensure that the

ICEIS 2005 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

430

class has all the attributes specified in the

meta-class definition.

Def5 A model m(mm, CC)

z A regarding meta-model mm

z A set CC is a collection of classes {c

, c

,…

}, with the property:

jijiji ccidcidcCCcc =⇒=∈∀ ..:,

Def6 A model fragment mf(m, CC

’

)

z A model m which it belongs to

z A subset CC’ is a collection of classes, with

the property:

CCmmfCCmfmf ..'.: ⊆∀

3.3 Definitions of Model

Transformations

Model transformations consist of a series of

transformation rules. Each rule embodies the relation

of source and target model. And each rule is refined

by a mapping. A mapping is a mathematical

function, described by several pattern definitions.

Def7 A model transformation rule r(mmf

mmf

) denotes there is a certain equivalence

between source model instance of mmf

and

target model of mmf

Def8 A relation R(mm

, mm

) is a model

transformation rule set {r

, r

, …, r

}, which is a

finite set of model transformation rules, with the

property:

:},1,0{,},1,0{ njik L∈∀∈∀

mmmmfrmmmmfr kjki .... =

, which determines

that all transformation rules of a model

transformation rule set define transformations

between the same two meta-models.

Def9 A mapping is a mathematical function

containing a number of pattern definitions. A

mapping extends a model transformation rule

and can be described as follows:

{

rextendsmfmfMAPPING ),( 10

),( BATIONTRANSFORMA

AmmfsSRC :::: 0

BmmftTAR :::: 1

−−−− ExpressionBooleanPRE:

−−−− ExpressionBooleanPOS :

ORidtidsMAP ..: →

:.VsattSOME

∈

∃

atttattsattALLFOR ..: →

−

−− patternTIONTRANSFORMAother

}

It denotes a mapping is responsible for

transforming a source model to a target model.

Each area beginning with TRANSFORMATION

label is called a pattern definition, in which the

id or certain attributes of a source class is

evaluated to the id or attributes of a target class.

3.4 Other Auxiliary Definitions

As we can see from Def9, model can be decomposed

into fragments and also can be integrated into a

whole.

Def10 meageable(CC

,CC

) iff

∧=

∈

∃ idcidcCCcCCc jibjai ..:,

∧=

∈

∃

nmjnnimm aaVcvaVcva (:.),(,.),(

)..)) mccmccvv jinm

≠

∨

≠

, i.e., two class

collections are meageable only if there exists no

class in both collections with an identical

identifier but with contradictory attribute values

or an contradictory meta-class.

Def11 merge(CC

,CC

)=CC’ iff

mergeable(CC

,CC

). The result of merge is a

class collection containing all classes in the

participating collection if these are mergeable.

Therein, CC’ is the set of classes which holds:

'..: CCcidCCidcCCc jbiaj ∈⇒

∉

∈

∀

CCcidCCidcCCc jajbj ∈⇒

∉

∈

∀

..:

:'',..,, CCcidcidcCCcCCc jibjai ∈∃=

∈

∀

∧

).'..'.( idcidcidcidc ji

∧=

∧

).'..'.( mccmccmccmcc ji

).'..'.( VcmccVcVc ji

∧

It denotes that to merge two class collections,

and all the same classes in separate collection are

merged into one and all the different classes are

preserved in the new collection.

Def12 mergeable(mf

, mf

) iff

)'.,'.(.. ccmfccmfmergeablemmfmmf baba

∧

i.e., two model fragments are mergeable only if

they are attached to the same model and their

class collections are mergeable.

Def13 A model fragment merging mfmerge(mf

)=mf’ iff

∧

),( ba mfmfmergeable

).,.('. ''' CCaCCaCC mfmfmergemf

, which

merges two model fragments mf

, mf

to a new

model fragment.

Def14 A transformation rule set R(mm

, mm

) is

complete when it holds:

:),,1,0{ Rrni i

∈

∀

1100 .... mmmmmmfrimmmmmmfri =

∧

000100 ).,,.,.( mmmmfrmmfrmmfrmerge n =

∧

100100 ).,,.,.( mmmmfrmmfrmmfrmerge n =

∧

4 MODEL TRANSFORMATION

FROM UML 1.0 TO UML 2.0

4.1 The Example Meta-models

To perform a model transformation requires clear

understanding of the abstract syntax and the

semantics of both the source and target. Meta-model,

which is used to define the abstract syntax and

A FORMAL LANGUAGE FOR MODEL TRANSFORMATION SPECIFICATION

431

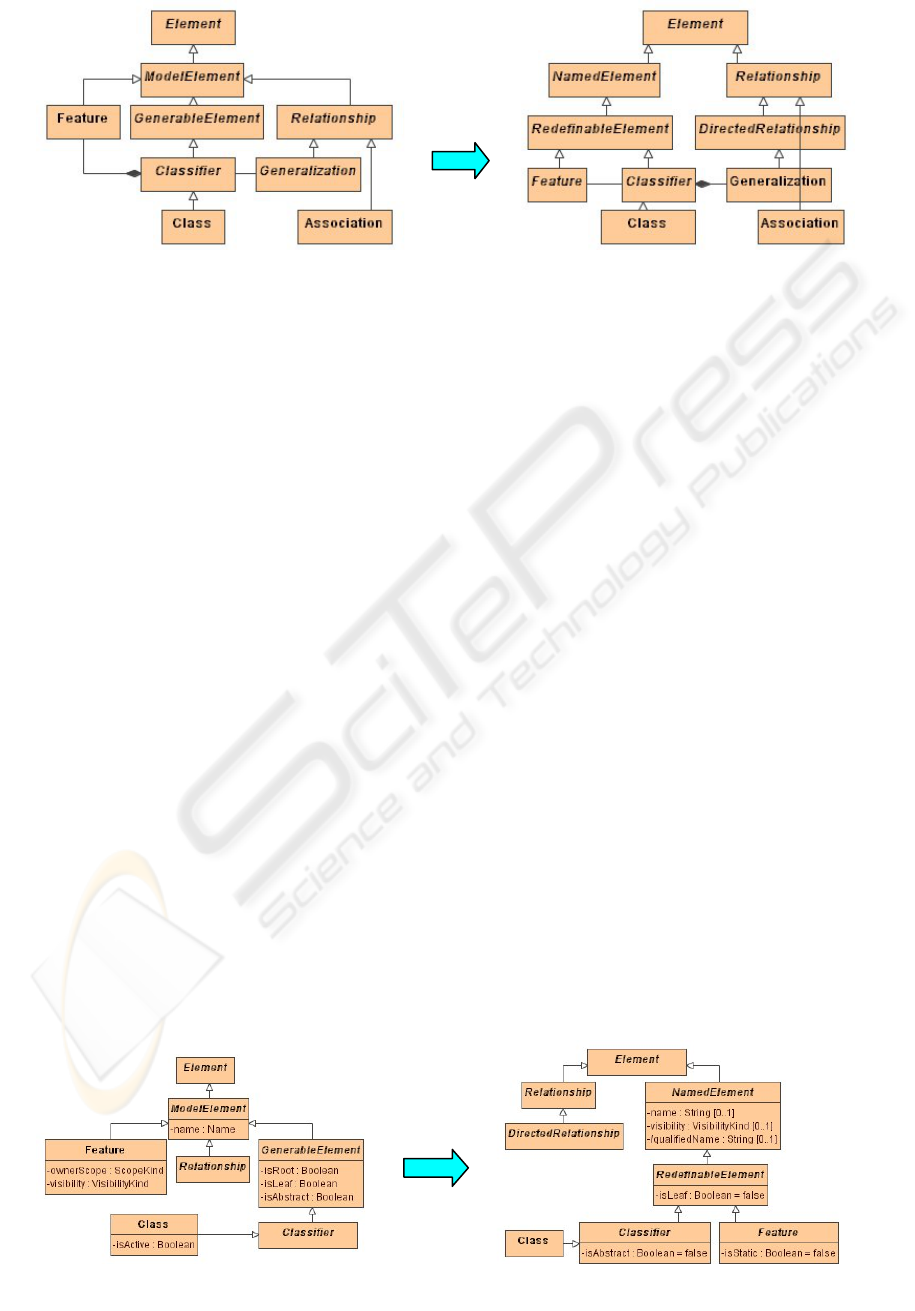
semantics of models, serves for this purpose. The

left part and right part of Figure 2 represent the core

UML 1.4 meta-model (OMG, 2001) and

corresponding core UML 2.0 meta-model (OMG,

2003) respectively.

4.2 Transformation Rules

Transformation rules should clearly express how the

source model and target model relates with each

other. But since the UML meta-model is rather

complex, this relation is not so distinctive. However,

it is not too difficult for us to find that the core UML

meta-model can be decomposed from such four

aspects as backbone, relationship, feature and

association. Accordingly, four rules can be

customized.

Informally speaking, the first rule r

identifies the

basic constructs required for elementary modelling.

Rule r

as shown in Figure 3, identifies model

elements that define relationships. Rule r

identifies

various kinds of features of elements. Rule r

distinguish relationship between association and

attribute. And all the four rules consist of the rule set

R. In order to express the intuitive knowledge about

how the models relate, graphical means are made

use of to depict transformation rules.

4.3 Formal Description

As the formal language and customized rules have

been presented, the relation between the UML 1.4

meta-model and UML 2.0 meta-model can be

described as R(mm

, mm

), in which, mm

is the

given source extent variable, mm

is the target extent

variable and R is the transformation rule set {r

, r

}. Rules in R can be respectively expresses as

(mmf

0,0

, mmf

1,0

), r

(mmf

0,1

, mmf

1,1

), r

(mmf

0,2

mmf

1,2

) and r

(mmf

0,3

, mmf

1,3

). Thereof, mmf

and

mmf

represent the source and target meta-model

fragment. Next, we should refine each rule by a

mapping. Take the implementation of r

for

example, the concrete and precise mapping and its

pattern definitions can be written as:

Figure 2: UML 1.4 Meta-model and UML 2.0 Meta-model.

MAPPING (mf

0,0

, mf

1,0

) extends r

{

TRANSFORMATION (Element, Element)

SRC: s: mmf

0,0

::Element

TAR: t: mmf

1,0

::Element

PRE: NONE

POS: NONE

MAP: s.id

t.id

→

TRANSFORMATION (ModelElement,

NamedElement)

SRC: s: mmf

0,0

:: ModelElement

TAR: t: mmf

1,0

:: NamedElement

PRE: s.parent instanceOf mmf

0,0

:: Element

POS: t.parent instanceOf mmf

1,0

:: Element

MAP: s.id

t.id s.name t.name

→ →

……

}

5 CONCLUSION

In this paper, we are engaged in the effort of

designing a formal language to describe model

Figure 3: Transformation Rule r

in Rule Set R.

ICEIS 2005 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

432

transformations. We argue that this formal

mechanism promises such advantages: 1. Expressive

power: formal definitions describe precise and

unambiguous relationships between the source and

models. 2. Incremental transformation: a model

fragment that describes an incremental change to the

source can be transformed to an additive model that

describes the corresponding incremental change for

the target, since transformation is based on

independent rules. 3. Easy for automation:

transformations are specified in declarative way

without involving implementing details.

Development tools can easily accept and understand

the formal input, hence convenient for automation of

transformation.

From the analysis, we believe that this solution

has general-purpose and can be applied in many

other specific domains. However, for the reason of

easy illustration, concepts that are not important for

our solution, such as method, multiplicity,

inheritance and constraint, are left out in our formal

language designing. And at present, the

implementing framework does not yet have tools to

support it. We hope that this formal language will be

further perfected and our implementing framework

can get full validation in the future.

REFERENCES

Joaquin Miller, Jishnu Mukerji, 2003. MDA Guide, OMG.

U.S.A., Version 1.0.1.

Shane Sendall, Wojtek Kozaczynski, 2003. Model

Transformation - the heart and soul of model-driven

software development. IEEE Software, Special Issue

on Model Driven Software Development, Vol.20, No.

Tata Consultancy Services, 2003. Revised submission for

MOF 2.0 Query / Views / Transformations RFP,

QVT-Partners. Version 1.1.

Krzysztof Czarnecki, Simon Helsen, 2003. Classification

of Model Transformation Approaches. In OOPSLA’03,

Workshop on Generative Techniques in the Context of

Model-Driven Architecture.

DSTC, IBM, CBOP, 2003. MOF Query / Views /

Transformations, QVT-Partners. 1

Revised

Submission.

Keith Daddy, Anna Gerber, Michael Lawley, Kerry

Raymond, Jim Steel, 2003. Model Transformation: A

declarative, reusable patterns approach. In EDOC’03,

Seventh International Enterprise Distributed Object

Computing Conference.

OMG, 2001. Unified Modelling Language Specification,

Version 1.4.

OMG, 2003. UML 2.0 Superstructure Specification,

Version 2.0.

A FORMAL LANGUAGE FOR MODEL TRANSFORMATION SPECIFICATION

433