DESIGN OF CONTINUOUS CALL MARKET WITH

ASSIGNMENT CONSTRAINTS

A. R. Dani

, V. P. Gulati

+ Institute for Development and Research in Banking Technology, Hyderabad, India

Arun K. Pujari*

* Department of Computer Science, University of Hyderabad, Hyderabad, India

Keywords: Continuous call double auctions, assignment

constraints, matching, clearing.

Abstract: Today’s companies increasingly use Internet as the common communication medium for commercial

transac

tions. Global connectivity and reach of Internet means that companies face increasing competition

from various quarters. This requires that companies optimize the way they do business, change their

business processes and introduce new business processes. This has opened up new research issues and

electronic or automated negotiation is one such area. Few companies have tried to introduce electronic

auctions for procurement and for trade negotiations. In the present paper, we propose a design of continuous

call market, which can help enterprises in electronic procurement as well as selling items electronically. The

design is based on double sided auctions, where multiple buyers and sellers submit their respective bids and

asks. Buyers and sellers can also specify assignment constraints. The main feature of our work is an

algorithm, which generates optimum matching with polynomial time complexity under assignment

constraints.

1 INTRODUCTION

Auction based protocols are widely used in

electronic commerce. An application of auction

theory in electronic procurement has also been

studied in (Eso, 2001), and it gives near optimal

solution to bid evaluation problem of the buyer. A

procurement process, which minimizes the cost

using auctions, has been proposed in (Bichler,

1999). Auctions provide an efficient price discovery

mechanism to sellers. Double-sided auctions

provide mechanism for clearing markets with

multiple buyers and sellers. Two main institutions

for double auctions are continuous double auction

and a clearing house or continuous call double

auction. In double auction, markets buyers submit

their bids and sellers submit asks. A transaction

occurs if the buyer’s bid price exceeds seller’s ask

price. A continuous double auction is one in which

many individual transactions are carried out and

trading does not stop. Call markets on the other

hand are periodic versions of continuous double

auctions, where bids from buyers and asks from

sellers are collected over a specified interval of time

and the market is cleared at the end of the interval.

The continuous call double auction is the oldest

practiced type of market for exchange of stocks,

where buyers and sellers post their respective bids

and asks continuously. In last few years, there has

been growing interest in Internet-based market

places.

In continuous call market, buyers submit bids

and

sellers submit asks continuously. These bids

and asks are matched periodically and the market

clears them. While clearing the call market, we need

to determine optimal matching of asks with bids. In

case, there are no assignment constraints, efficient

algorithms exists to determine the optimum

allocation. This problem of matching asks and bids

can become complex in case there are assignment

constraints. The simplest type of assignment

constraints can be of the types where a bid can be

matched with some of the asks. Other types of

constraints are the ones where the buyer specifies a

bid to be all or nothing type. In such cases, the

buyer’s demand should be completely satisfied. In

some cases, the demand can be indivisible, meaning

that a demand from an ask cannot be partly matched

182

R. Dani A., P. Gulati V. and K. Pujari A. (2005).

DESIGN OF CONTINUOUS CALL MARKET WITH ASSIGNMENT CONSTRAINTS.

In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 182-187

DOI: 10.5220/0002550001820187

 SciTePress

with supply from an ask. Such constraints (known

as indivisible demand constraints (Kalagnanam,

2001)) are not considered here. In this paper, we

consider matching problem with multiple

assignment constraints.

The main contribution of this paper is the

development of an algorithm to match asks and bids

under assignment constraints. This algorithm is

fundamental to the design of continuous call market

presented here. This mechanism helps enterprises in

electronic procurement as well as to sell items and

also specify constraints on different attributes. The

main example presented here is about paper

exchange, however the formulation is a general one

and can be used in other similar cases. One of the

important features of our algorithm is that it takes

into account other attributes (like width) apart from

common attributes like price and quantity. Another

important feature is that it obtains optimum

matching under different types of assignment

constraints. While submitting bids and asks, buyers

and sellers can specify assignment constraints.

Apart from this, it also handles implicit assignment

constraints. It is also shown that our algorithm can

solve the problem with worst case time complexity

of O(n

). The algorithm can work in cases where

there are no assignment constraints and price and

quantity are the only decision attributes. Thus, the

problem is addressed in much more general settings.

The rest of the paper is organized as follows, in

section 2, we discuss how implicit and explicit

assignment constraints can arise in different

situations. The related work is also discussed in this

section. In section 3, we first present the

formulation of the problem. The problem has been

formulated as 0-1 programming problem. We have

discussed some of the related issues here. Our

algorithm is presented in section 4. We also discuss

related issues are discussed. Experimental results

and implementation details like different types of

Unified Modeling Language (UML) diagrams and

modules are discussed in section 5 and we conclude

in section 6.

2 EXAMPLE AND RELATED

WORK

Most of the stock exchanges like New York, Tokyo

(McCabe, 1992), (Arizona Stock Exchange) and

(Optimark) have implemented online trading

systems based on double auction mechanism. Apart

from financial markets, double-auction-based

mechanisms have been widely used in multi

commodity stock exchanges like National Stock

Exchange of India. In all these cases, the

commodity is substitutable and buyers do not have

any preference for a particular seller, much in the

same way as goods like stocks, do not have any

differentiating features apart from price and

quantity. In all these cases, asks and bids can be

matched without any types of assignment

constraints. Only constraints that are imposed by

buyers or sellers can be either or nothing type of bid

(i.e. fulfilling complete demand), or minimum

required demand (minimum quantity to buy or sell).

In these cases, price and quantity become the only

differentiating factor and matching is done based on

them. However, in some cases, as indicated in the

following example from the process industry, the

price and quantity need not be the only

differentiating factor and there can be different types

of assignment constraints. Suppose that in a paper

exchange following asks (Table 1) from different

sellers, supplying paper of different grades, widths

(in cm) and quantities (tons) are received. The bids

received from different buyers indicating the price

they are willing to pay, quantities required, grades of

paper required and widths required, are listed in

Table 2. Suppose that the sellers are supplying

papers of different grades as indicated by positive

integer 1,2,3 etc. The buyer also indicates the type

of paper required by specifying its grade. Suppose

that higher-grade paper is represented by higher

integer value. It can be seen that there are certain

assignment constraints in the above example, which

must be considered while matching. The assignment

constraints for matching are:

A buyer’s bid requiring paper of grade 3, cannot be

matched with an ask supplying paper of grade 1 or 2,

as he requires paper of grade 3 only. In some cases,

the buyer may specify that the paper of higher grade

can be accepted. In this case, the demand for paper

of grade 3 can be satisfied by supply with grade 3 or

above. It may be possible to match a bid with an ask

of higher grade.

Another constraint can be the width of the paper

required. It can be seen from the above example that

the bid from second buyer requiring paper of width

1200 cm can be matched with only those asks,

Table 1 : Asks for different sellers in Paper Exchange

Seller Price Width (cm) Supply

(Quantity)

Grade

1 100 1000 6 1

2 105 1000 2 2

3 110 2000 5 3

4 114 1200 5 4

5 119 1600 3 1

DESIGN OF CONTINUOUS CALL MARKET WITH ASSIGNMENT CONSTRAINTS

183

which supply paper of width 1200 cm or more. It

can also be seen that the supply from ask can be

used to satisfy the demand of buyers 3 and 4 by

cutting the paper of width 1600 cm into two rolls of

800 cm each.

An algorithm to match these bids and asks and

provide optimum matching, based price discovery

mechanism proposed in (Gjerstad 1998), when there

are no assignment constraints, is presented in

(Kalagnanam, 2001). In this case, the price p

determined by constructing the aggregate supply and

demand curves. This price is the point of

intersection of these two curves and is used as the

clearing price. All the bids having prices above it

and asks having lower prices are considered for

matching. The highest price bid is matched with the

lowest price ask. The matching continues

sequentially till all selected bids and asks are

matched. In some cases, as shown in the example of

paper exchange, there can be assignment constraints

on different attributes (like grade, width etc.). If

there are no indivisible demand bid constraints, the

matching assignment problem can be formulated as

network flow problem (

Kalagnanam, 2001), (Ahuja,

1993). This problem is converted into a network

flow problem such that there is a starting node

known as source node, intermediate node consisting

of all bids and asks and ending node known as sink

node. The arcs between these nodes are constructed

using the difference between the prices as cost and

quantity as weight. The cost is set to 0 for the arcs

from starting node and arcs ending in sink node.

This problem is then solved as the network flow

optimization problem formulating either as

maximization of matching of demand and supply or

as profit of the auction problem. There are many

algorithms available to solve this problem. The

complexity of maximum flow problem i.e. matching

of demand and supply is O (nm+ n

log n)]. In this

case, n represents number of nodes and m number of

edges. In cases where demand is indivisible, finding

optimal matching requires solving of NP-hard

optimization problems like multiple knapsack

problem, bin packing problem or generalized

assignment problems (Martello, 1989), (Garey,

1979), (Sandholm, 1999),

Kalagnanam, 2001)

(Cheriyan, 1979).

Table 2 : Bids from different buyers in Paper Exchange

Buyer Price Width Demand Grade

1 175 2000 5 3

2 170 1200 5 4

3 165 800 3 1

4 163 800 3 1

To the best of our knowledge, no work related to

matching in the presence of assignment constraints

has been reported. In the present work, an algorithm

to obtain optimum matching in case of assignment

constraint has been developed.

3 PROBLEM FORMULATION

One of the important feature of our design of

Continuous Call Market with a assignment

constraint is an algorithm to find out the optimum

assignment of bids and asks. It always generates

optimum assignment in case of assignment

constraints as well as in unconstrained case. In case

of assignment constraints, one approach can be to

group set of n asks and m bids into different sets of

asks A

,..A

and bids, B

,..B

. Each set

is formed by asks and bids which satisfy a particular

constraint (e.g. Grade constraint) and are disjoint.

Let A

be set of asks for which Grade attribute has

value 1, A

be the set of asks for which grade

attribute has value 2 and so on. Once the asks and

bids can be grouped in this way, the matching can be

done for each subset of asks and bids separately.

However, this approach can be used efficiently when

the constraints are of equality type. It will be

difficult to group bids exactly where required paper

grade is greater than 3 or width required is 800 cm.

In the second case, the bid can possibly be matched

with any ask where width is 800 cm or more. There

can also be another problem. Suppose that a bid,

which requires paper width of 800 cm (quantity 5

tons) is matched with an ask of 1200 cm (quantity 5

tons). Then remaining part of the ask i.e. 400cm of

width (quantity 5 tons) will either be wasted or

should be moved to another set. The algorithms

presented in

(Kalagnanam, 2001) also describe

matching on two attributes, namely, price and

quantity. We present an algorithm, which takes into

account the size factor, apart from price and

quantity. We have formulated the problem as 0-1

programming problem. The details of our

formulation can be seen in (Dani 2005).

4 ALGORITHM FOR ASSIGNMENT

Suppose that there are n bids and m asks. In our

algorithm, assignment of the asks to bids is done as

follows:

ICEIS 2005 - SOFTWARE AGENTS AND INTERNET COMPUTING

184

1. The assignment starts from the highest price bid.

In the first stage, the set of asks with the highest unit

contribution are determined. Then we obtain

maximum quantity that can be assigned. Then

assignment is carried out. We combine asks with

the same unit contribution and always determine

maximum possible quantity that can be assigned. If

ask quantity is less than the bid quantity, then the

ask is marked as temporarily assigned, while bid is

marked as partly assigned and assignment continues

from the next ask onwards till complete demand is

fulfilled. The bid and/or all asks are marked as

assigned. If ask has more quantity, then bid is

marked as assigned and ask is marked as partly

assigned. Then assignment is continued in

decreasing order of price for bids.

2. Initially a table indicating demand for different

width is constructed. If the ask size is multiple of

bid size (e.g. bid width 800 cm and ask width 1600

cm), then this table is used to see whether there is

demand for the remaining width (i.e. 800 cm). If

there is demand, then wastage parameter is set to 0.

This is helpful in situations to decide, whether bid is

to be matched with ask of 1600 cm or 1000 cm.

Here matching of current bid with ask width of 1000

cm will show lesser wastage than that of 1600 cm.

However, if there is demand for 800 cm, then it can

be matched with the ask of 1600 cm width so that

wastage is minimized.

The assignment is continued till one of the three

conditions holds (i) no ask is left (ii) no bid is left

(iii) when ask price exceeds that of bid price. In our

solution, assignment is carried out if bid price is

either more than ask price or both are same. This

assumption is reasonable in the sense that in most

exchanges asks are cleared with bids of same or

higher price. It can also be seen in (

Kalagnanam,

2001)

, that equilibrium price is first obtained. This

price is used to determine the asks and bids which

can be cleared (asks below this price and bids above

it). Let A be the list of asks and B be the list of bids.

Algorithm findopasg (A,B) /* Main Algorithm */

Call Create_ Size_Demand_Table(bids) ;

While ( there is unassigned bid in B ){

Call get_next_unassigned_bid(bids) ;

Call get_opt_ask(bid_quantity,bid_size,) ;

Call assignment(bid,ask,bid_quantity) } return ; } /*

End of main algorithm **/

/** Function to create Size Demand Table **/

create_Size_Demand_Table(bids) {

while ( there is next bid) { get bid_size, bid_quantity ;

call search_table(bid_size,table_size) ;

if ( .not.. found )then { increase current_index by 1 ;

store bid_size to search_table(current_index,1) ;

store bid_quantity to search_table(current_index,2) ;

set table_size to current_index ;}

else{ add bid_quantity to search_table(current_index,2);}

read next_bid ; } return ; }

/** Function to search table **/

Search_Table(bid_size,table_size) {

while ( i <= table_size ) {

If (search_table(I,1) = bid_size) then {set

current_index to i ; return .true ; }

else {increase i by 1 ;} return false; }

/** This function gets next highest price bid **/

get_next_unassigned _bid(bids) {

while ( there is unassigned bid) {

if (bid_price > max_price) then { set max_price to

bid_price; set bid to current_bid ; } } return ; }

/** Function to get ask which brings maximum

improvement **/

get_opt_ask(bid_quantity,bid_size) {

while ( there is unassigned ask) { call

get_next_unassigned_ask(asks,bid) ;

if ( ask_quantity >= bid_quantity and ask_size >=

bid_size) then qty_asg = bid_quantity end if ;

if ( bid_quantity < ask _quantity ) then qty_asg =

qty_asg_+ bid_quantity ; mark ask temp_assigned ;

call cal_obv(bid,ask,qty_asg) ;

if ( ov > max_imp ) then { ask_ret = current_ask ;

max_imp = ov ; } return ; }

/** This function gets next lowest price ask **/

get_next_unassigned _ask(asks,bid) {

while ( there is unassigned and unmarked ask } {

if ( (bid_price < min_price) and can be assigned to bid )

then { set min_price to ask_price;

set ask to current_ask; } } return ; }

/ ** This function calculates the contribution **/

cal_obv(bid,ask,qty_asg) { net_surplus = ( bid_price –

ask_prce ) * bid_quantity ;

wastage = ( ask_size – bid_size ) * bid_quantity ; call

search_table(wastage,table_size); if found then set

wastage = 0 ; ov = net_surplus + wastage ; return }

/** This function does the assignment **/

assignment(bid,ask,qty_asg) {

assign ask to bid ; quantity_assigned = qty_asg ;

if ( qty_asg = bid_quantity ) then mark bid as assigned ;

if ( qty_asg = ask_quantity and ( ask_size – bid_size = 0 )

) then mark ask as assigned ;

if ( qty_asg < bid_quantity ) then bid_quantity =

bid_quantity – qty_asg ;

if ( qty_asg < ask_quantity ) then ask_quantity =

ask_quantity – qty_asg ;

if ( ( ask_size – bid_size) > 0 ) then ask_size = ask_size-

bid_size; return ; }

Example: The working of the algorithm is

illustrated in the following example with five asks

and five bids. The assignment constraints are

basically size constraints i.e. a bid can be matched

with an ask of same or higher size. The wastage is 8

here. The output can be seen in Table 3.

DESIGN OF CONTINUOUS CALL MARKET WITH ASSIGNMENT CONSTRAINTS

185

Table 3 : Bids & Asks

–

timum Solution

5 EXPERIMENTAL RESULTS

AND DISCUSSION

The algorithm has been implemented in C++. The

data sets of different sizes, with each data set

consisting of ask price, quantity, ask size, bid size,

bid price and bid quantity, were generated randomly.

The number of elements in each data set varied from

5 to 100. The results were compared with

unconditional optimum solution and some solutions

obtained with the help of MATLAB package. It has

also been seen that if size of ask is constant and bid

sizes are variable but take few values (as in most of

the practical cases), then we can ignore the wastage

factor. The approach can be to obtain maximum

surplus and then readjust assignment without

affecting value of objective function. It can also be

seen that time complexity of our algorithm is always

polynomial. In this algorithm, a matching ask which

generates maximum improvement can be obtained

by scanning unassigned asks at any point of time. In

the first instance, there will be n unassigned asks, in

the next instance, there will be (n-1) unassigned asks

and so on. So, in all the solution will require to scan

n(n-1)/2 asks. So the time complexity will be

polynomial and of order O(n

) or O(mn). Apart

from this, the demand size table and getting

minimum or maximum price asks/bids can be

obtained with linear time complexity. So overall the

time complexity will always be polynomial. This

compares quite favorably with the complexity

O(nm+ n

log n)] of algorithm presented in

(Kalagnanam, 2001) apart from its simplicity for

large instance of n and m. The comparison can be

seen in Figure 1.

5.1 Continuous Call Market System

Design and Implementation

The different entities in our continuous call market

are buyers, sellers and auctioneers. The bids and

asks are continuously submitted by buyers and

sellers. At periodic intervals, asks and bids are

matched to find optimum assignment of asks and

bids, which is worked out by our algorithm and

market clears. The payoff is computed and the

process is repeated. The UML State Chart Diagram

captures different states of our Continuous Call

Market in Figure 2. The UML activity diagram is

shown in Figure 3. The different modules in the

system are:

User Registration Module: This module helps

buyers and sellers to register with the system.

Notification Module: It notifies users about

different activities. Once auctions are notified,

buyers and sellers can submit respective bids and

asks. It also notifies the result of the clearing

process.

Web Interface: This interface helps buyers and

Figure 1: Comparison of Results

Bid Price Qty Size Ask Price Qty Size

Bid Ask Spread Qty

Net

Surplus

Wastage

1 187 11 8 1 101 23 8

1 1 86 11 946

2 181 12 4 2 109 8 12

2 1 80 12 960

3 173 23 8 3 121 6 12

3 4 38 4 152

4 161 10 12 4 135 4 8

3 5 22 19 418

5 157 8 8 5 151 23 8

4 2 52 8 416

64 64

43 40 2 80

5 3 36 4 144

55 6 4 24

64 3140

Number of Bids

Propose

Algorith

Net work

Algorith

ICEIS 2005 - SOFTWARE AGENTS AND INTERNET COMPUTING

186

istered

sellers to submit bids and asks respectively. It also

helps buyers and sellers to specify the attributes and

constraints.

Validation Module: This module validates the data

submitted. It returns invalid bids and asks.

Scheduler Module: This module schedules different

activities like notification, closure of bid and ask

acceptance, clearing of market, etc.

Clearing Module: It first formulates the matching

problem depending upon the attributes and

constraints specified. It then implements the

matching algorithm described in section 4 of the

paper. It finds out optimum assignment of asks and

bids.

Payoff Module: It computes the payoff of buyers

and sellers.

6 CONCLUSION AND FUTURE

WORK

In this paper, we have presented design of

Continuous Call Market, which can handle

assignment constraints. Its main component is the

market clearing algorithm, which generates optimum

solution to the problem of matching of asks and bids

in case of assignment constraints. This can help

enterprises to procure items required as well as sell

them. They can also specify the assignment

constraints on different attributes, so the problem is

handled on more general settings. The algorithm

can also handle unconstrained cases. The future

work includes extending this work to solve the

problem with indivisible demand bid constraints and

security component.

REFERENCES

Ahuja K., Magnanti T. L., Orlin B., 1993. Network Flows,

Arizona Stock Exchange, www.azx.com, ISBN 0-13-6175-

49-X, Prentice Hall.

Bichler M., Kaukal Marion, Segev Arie, 1999. Multi

Attribute Auctions for Electronic Procurement, In the

proceedings of First IBM IAC Workshop on Internet

Based Negotiation Technologies, Yorktown Heights,

NY, Marz,

Cheriyan J., Hagerup T., 1995. A Randomized Maximum

Flow Algorithm, SIAM Journal of Computing, 25(6),

Pages 1144-1170,

Dani A. R. , Pujari Arun K., Gulati V. P.,2005. Continous

Call Auctions With Indivisibility Constraints, To

appear in IEEE International Conference in E-

Technology, E-Commerce and E-Services, Hongkong,

March 29-April 1, 2005

Eso M., Ghosh S., Kalagnanam J., Ladanyi L., 2001. Bid

evaluation in procurement auctions with piece-wise

linear supply curves, IBM Research Report RC 22219

Gjerstad S., Dickhaut J., 1998. Price Formation in Double

Auction, Games and Economic Behavior, 22(1), Pages

1-29,

Garey M.R., D.S. Johnson D.S., 1979. Computers and

Intractability, A Guide to Theory of NP Completeness,

W. H. Freeman and Company, New York,

Kalagnanam Jayant R., Devenport Andrew J.,.Lee Ho, S,

Computational Aspects of Clearing Continuous Call

Double Auction with Assignment Constraints and

Indivisible Demand, Electronic Commerce Research ,

Volume 1, Issue 3 (July 2001),

Pages: 221 - 238

McCabe K.A., Rassenti S. J. and Smith V. L., 1992.

Designing Call Auctions Institutions: Is Double Dutch

the Best? The Economic Journal, Pages 9-23

Martello S., Toth P., 1989. Knapsack problem. John Wiley

and Sons Limited, New York

National Stock Exchange of India, www.nse-india.com

OPTIMARK, Website www.optimark.com

T. Sandholm, 1999. An Algorithm for Optimal Winner

Determination in Combinatorial Auction, In

proceedings of IJCAI 1999, Morgan Kaufmann.

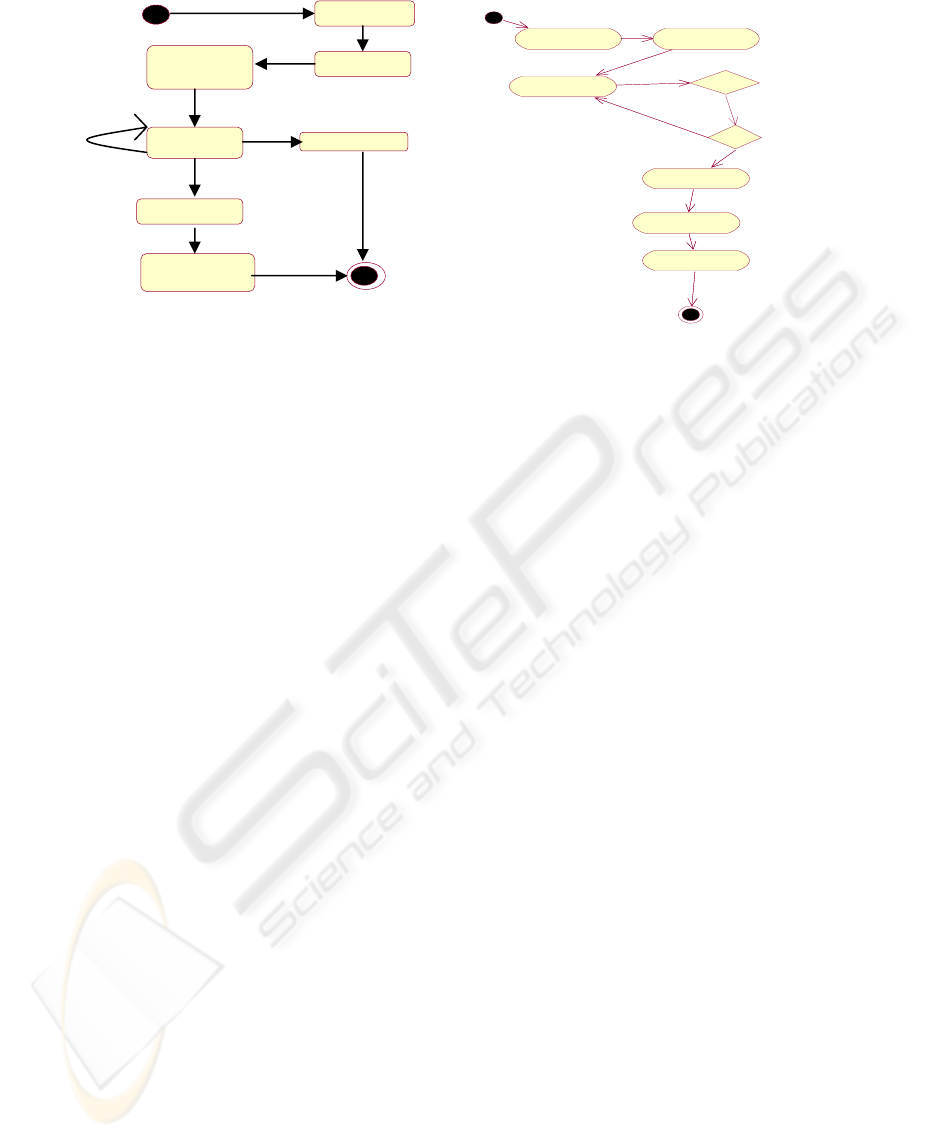
Figure 3: Activity diagram of Continuous Call Market

Notify Users

Accept Bids

and Asks

Is Data Valid?

Y/N

Match and

Clear Market

Is Period Over ?

Y/N

Compute Pay

Off

Notify Result

Bid/Ask

Notified

Submitted

Data

Rejected

Validated

cceptance

Closed

Matched and

Cleared

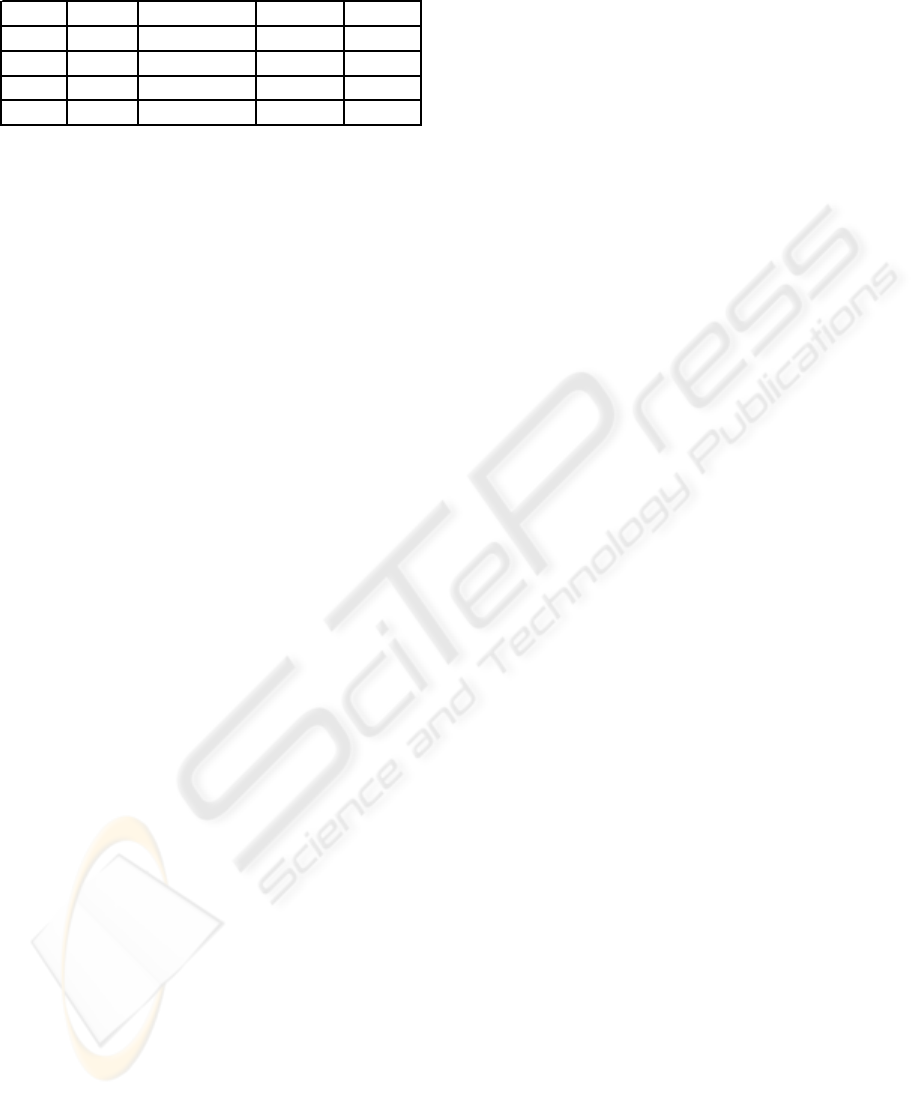
Figure 2: State Transition diagram of Continuous Call

Market

DESIGN OF CONTINUOUS CALL MARKET WITH ASSIGNMENT CONSTRAINTS

187