
WEB RECOMMENDATION SYSTEM BASED ON A
MARKOV-CHAIN MODEL
Francois Fouss, Stephane Faulkner, Manuel Kolp, Alain Pirotte, Marco Saerens
Information Systems Research Unit
IAG, Universite catholique de Louvain, Place des Doyens 1, B-1348 Louvain-la-Neuve, Belgium
Information Systems Research Unit
Department of Management Science, Universite of Namur, Rempart de la Vierge 8, B-5000 Namur, Belgium
Keywords:
Collaborative Filtering, Markov Chains, Multi Agent System.
Abstract:
This work presents some general procedures for computing dissimilarities between nodes of a weighted, undi-
rected, graph. It is based on a Markov-chain model of random walk through the graph. This method is applied
on the architecture of a Multi Agent System (MAS), in which each agent can be considered as a node and
each interaction between two agents as a link. The model assigns transition probabilities to the links between
agents, so that a random walker can jump from agent to agent. A quantity, called the average first-passage
time, computes the average number of steps needed by a random walker for reaching agent k for the first time,
when starting from agent i. A closely related quantity, called the average commute time, provides a distance
measure between any pair of agents. Yet another quantity of interest, closely related to the average commute
time, is the pseudoinverse of the Laplacian matrix of the graph, which represents a similarity measure be-
tween the nodes of the graph. These quantities, representing dissimilarities (similarities) between any two
agents, have the nice property of decreasing (increasing) when the number of paths connecting two agents
increases and when the “length” of any path decreases. The model is applied on a collaborative filtering task
where suggestions are made about which movies people should watch based upon what they watched in the
past. For the experiments, we build a MAS architecture and we instantiated the agents belief-set from a real
movie database. Experimental results show that the Laplacian-pseudoinverse based similarity outperforms all
the other methods.
1 INTRODUCTION
Gathering product information from large electronic
catalogue on E-Commerce sites can be a time-
consuming and information-overloading process. As
information becomes more and more available on the
World Wide Web, it becomes increasingly difficult for
users to find the desired product from the millions
of products available. Recommender systems have
emerged in response to these issues (Breese et al.,
1998), (Resnick et al., 1994), or (Shardanand and
Maes, 1995). They use the opinions of members of
a community to help individuals in that community to
identify the information or products most likely to be
interesting to them or relevant to their needs. As so,
recommender systems can help E-commerce in con-
verting web surfers into buyers by personalization of
the web interface. They can also improve cross-sales
by suggesting other products in which the consumer
might be interested. In a world where an E-commerce
site competitors are only two clicks away, gaining
consumer loyalty is an essential business strategy. In
this way, recommender systems can improve loyalty
by creating a value-added relationship between sup-
plier and consumer.
One of the most successful technologies for recom-
mender systems, called collaborative filtering (CF),
has been developed and improved over the past
decade. For example, the GroupLens Research sys-
tem (Konstan et al., 1997) provides a pseudony-
mous CF application for Usenet news and movies.
Ringo (Shardanand and Maes, 1995) and MovieLens
(Sarwar et al., 2001) are web systems that generate
recommendations on music and movies respectively,
suggesting collaborative filtering to be applicable to
many different types of media. Moreover, some of the
highest commercial web sites like Amazon.com, CD-
Now.com, MovieFinder.com and Launch.com made
use of CF technology.
Although CF systems have been developed with
success in a variety of domains, important research
issues remain to be addressed in order to overcome
56
Fouss F., Faulkner S., Kolp M., Pirotte A. and Saerens M. (2005).
WEB RECOMMENDATION SYSTEM BASED ON A MARKOV-CHAIN MODEL.
In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 56-63
DOI: 10.5220/0002550700560063
Copyright
c
SciTePress

two fundamental challenges: performances (e.g., the
CF system can deal with a great number of consumers
in a reasonable amount of time) and accuracy (e.g.,
users need recommendations they can trust to help
them find products they will indeed like).
This paper addresses both challenges by propos-
ing a novel method for CF. The method includes a
procedure based on a Markov-chain model used for
computing dissimilarities between nodes of an undi-
rected graph. This procedure is applied on the ar-
chitecture of a Multi Agent System (MAS), in which
each agent can be considered as a node and each in-
teraction among agents as a link. Moreover, MAS ar-
chitectures are gaining popularity over classic ones to
build robust and flexible CF applications (Wooldridge
and Jennings, 1994) by distributing responsabilities
among autonomous and cooperating agents.
For illustration purposes, we consider in this work
a simple MAS architecture which supports an E-
commerce site selling DVD movies. The MAS ar-
chitecture is instantiated with three sets of agents:
user agent, movie agent and movie-category agent,
and two kinds of interactions: between user agent
and movie agent (has
watched), and between movie
agent and movie-category agent (belongs
to). Then,
the procedure allows to compute dissimilarities be-
tween any pair of agents:
• Computing similarities between user agents allows
to cluster them into groups with similar interest
about bought movies.
• Computing similarities between user agent and
movie agents allows to suggest movies to buy or
not to buy.
• Computing similarities between user agent and
movie-category agents allows to attach a most rel-
evant category to each user agent.
To compute the dissimilarities, we define a
random-walk model through the architecture of the
MAS by assigning a transition probability to each link
(i.e., interaction instance). Thus, a random walker can
jump from neighbouring agents and each agent there-
fore represents a state of the Markov model.
From the Markov-chain model, we then compute
a quantity, m(k|i), called the average first-passage
time (Kemeny and Snell, 1976), which is the average
number of steps needed by a random walker for reach-
ing state k for the first time, when starting from state i.
The symmetrized quantity, n(i, j) = m(j|i)+m(i|j),
called the average commute time (Gobel and Jagers,
1974), provides a distance measure between any pair
of agents. The fact that this quantity is indeed a dis-
tance on a graph has been proved independently by
Klein & Randic (Klein and Randic, 1993) and Gobel
& Jagers (Gobel and Jagers, 1974).
These dissimilarity quantities have the nice prop-
erty of decreasing when the number of paths connect-
ing the two agents increases and when the “length” of
any path decreases. In short, two agents are consid-
ered similar if there are many short paths connecting
them.
To our knowledge, while being interesting alterna-
tives to the well-known “shortest path” or “geodesic”
distance on a graph (Buckley and Harary, 1990), these
quantities have not been exploited in the context of
collaborative filtering; with the notable exception of
(White and Smyth, 2003) who, independently of our
work, investigated the use of the average first-passage
time as a similarity measure between nodes. The
“shortest path” distance does not have the nice prop-
erty of decreasing when connections between nodes
are added, therefore facilitating the communication
between the nodes (it does not capture the fact that
strongly connected nodes are at a smaller distance
than weakly connected nodes). This fact has already
been recognized in the field of mathematical chem-
istry where there were attempts to use the “commute
time” distance instead of the “shortest path” distance
(Klein and Randic, 1993). Notice that there are many
different ways of computing these quantities, by us-
ing pseudoinverses or iterative procedures; details are
provided in a related paper.
Section 2 introduces the random-walk model -a
Markov chain model. Section 3 develops our dissim-
ilarity measures as well as the iterative formulae to
compute them. Section 4 specifies our experimental
methodology. Section 5 illustrates the concepts with
experimental results obtained on a MAS instantiated
from the MovieLens database. Section 6 is the con-
clusion.
2 A MARKOV-CHAIN MODEL OF
MAS ARCHITECTURE
2.1 Definition of the weighted graph
A weighted graph G is associated with a MAS archi-
tecture in the following obvious way: agents corre-
spond to nodes of the graph and each interaction be-
tween two agents is expressed as an edge connecting
the corresponding nodes.
In our movie example, this means that each instan-
tiated agent (user agent, movie agent, and movie cat-
egory agent) corresponds to a node of the graph, and
each has_watched and belongs_to interaction
is expressed as an edge connecting the corresponding
nodes.
The weight w
ij
> 0 of the edge connecting node
i and node j (say there are n nodes in total) should
be set to some meaningful value, with the following
convention: the more important the relation between
WEB RECOMMENDATION SYSTEM BASED ON A MARKOV-CHAINMODEL
57

node i and node j, the larger the value of w
ij
, and
consequently the easier the communication through
the edge. Notice that we require that the weights be
both positive (w
ij
> 0) and symmetric (w
ij
= w
ji
).
The elements a
ij
of the adjacency matrix A of the
graph are defined in a standard way as
a
ij
=
w
ij
if node i is connected to node j
0 otherwise
(1)
where A is symmetric. We also introduce the Lapla-
cian matrix L of the graph, defined in the usual man-
ner:
L = D − A (2)
where D = diag(a
i.
) with d
ii
= [D]
ii
= a
i.
=
P
n
j=1
a
ij
(element i, j of D is [D]
ij
).
We also suppose that the graph is connected; that
is, any node can be reached from any other node of
the graph. In this case, L has rank n − 1, where n is
the number of nodes (Chung, 1997). If e is a column
vector made of 1 (i.e., e = [1, 1, . . . , 1]
T
, where T de-
notes the matrix transpose) and 0 is a column vector
made of 0, Le = 0 and e
T
L = 0
T
hold: L is doubly
centered. The null space of L is therefore the one-
dimensional space spanned by e. Moreover, one can
easily show that L is symmetric and positive semidef-
inite (Chung, 1997).
Because of the way the graph is defined, user
agents who watch the same kind of movie, and there-
fore have similar taste, will have a comparatively
large number of short paths connecting them. On the
contrary, for user agents with different interests, we
can expect that there will be fewer paths connecting
them and that these paths will be longer.
2.2 A random walk model on the
graph
The Markov chain describing the sequence of nodes
visited by a random walker is called a random walk on
a weighted graph. We associate a state of the Markov
chain to every node (say n in total); we also define
a random variable, s(t), representing the state of the
Markov model at time step t . If the random walker is
in state i at time t, we say s(t) = i.
We define a random walk by the following single-
step transition probabilities
P
(s(t + 1) = j|s(t) = i) =
a
ij
a
i.
= p
ij
,
where a
i.
=
n
X
j=1
a
ij
In other words, to any state or node i, we asso-
ciate a probability of jumping to an adjacent node,
s(t + 1) = j, which is proportional to the weight
w
ij
of the edge connecting i and j. The transition
probabilities only depend on the current state and not
on the past ones (first-order Markov chain). Since the
graph is totally connected, the Markov chain is irre-
ducible, that is, every state can be reached from any
other state. If this is not the case, the Markov chain
can be decomposed into closed sets of states which
are completely independent (there is no communica-
tion between them), each closed set being irreducible.
Now, if we denote the probability of being in state
i at time t by x
i
(t) =
P
(s(t) = i) and we define
P as the transition matrix whose entries are p
ij
=
P
(s(t+1) = j|s(t) = i), the evolution of the Markov
chain is characterized by
x
i
(0) = x
0
i
x
i
(t + 1) =
P
(s(t + 1) = i)
=
n
X
j=1
P
(s(t + 1) = i|s(t) = j) x
j
(t)
=
n
X
j=1
p
ji
x
j
(t)
Or, in matrix form,
x(0) = x
0
x(t + 1) = P
T
x(t)
(3)
where T is the matrix transpose.
This provides the state probability distribution
x(t) = [x
1
(t), x
2
(t), ..., x
n
(t)]
T
at time t once the
initial probability density, x
0
, is known. For more de-
tails on Markov chains, the reader is invited to consult
standard textbooks on the subject (Bremaud, 1999),
(Kemeny and Snell, 1976), (Norris, 1997).
3 AVERAGE FIRST-PASSAGE
TIME AND AVERAGE
COMMUTE TIME
In this section, we review two basic quantities that
can be computed from the definition of the Markov
chain, that is, from its probability transition matrix:
the average first-passage time and the average com-
mute time. Relationships allowing to compute these
quantities are derived in a heuristic way (see, e.g.,
(Kemeny and Snell, 1976) for a more formal treat-
ment).
3.1 The average first-passage time
The average first-passage time, m(k|i) is defined as
the average number of steps a random walker, start-
ing in state i 6= k, will take to enter state k for the first
time (Norris, 1997). More precisely, we define the
ICEIS 2005 - SOFTWARE AGENTS AND INTERNET COMPUTING
58

minimum time until absorption by state k as T
ik
=
min (t ≥ 0 | s(t) = k and s(0) = i) for one realiza-
tion of the stochastic process. The average first-
passage time is the expectation of this quantity, when
starting from state i: m(k|i) = E [T
ik
|s(0) = i].
We show in a related paper how to derive a re-
currence relation for computing m(k|i) by first-step
analysis.
We obtain
m(k|i) = 1 +
n
X
j=1;j6=k
p
ij
m(k|j), for i 6= k
m(k|k) = 0
(4)
These equations can be used in order to iteratively
compute the first-passage times (Norris, 1997). The
meaning of these formulae is quite obvious: in order
to go from state i to state k, one has to go to any ad-
jacent state j and proceed from there.
3.2 The average commute time
We now introduce a closely related quantity, the aver-
age commute time, n(i, j), which is defined as the
average number of steps a random walker, starting
in state i 6= j, will take before entering a given
state j for the first time, and go back to i. That is,
n(i, j) = m(j|i) + m(i|j). Notice that, while n(i, j)
is symmetric by definition, m(i|j) is not.
3.3 The average commute time is a
distance
As shown by several authors (Gobel and Jagers,
1974), (Klein and Randic, 1993), the average com-
mute time is a distance measure, since, for any states
i, j, k:
n(i, j) ≥ 0
n(i, j) = 0 if and only if i = j
n(i, j) = n(j, i)
n(i, j) ≤ n(i, k) + n(k, j)
Another important point not proved here is that L
+
is a matrix whose elements are the inner products of
the node vectors embedded in an Euclidean space pre-
serving the ECTD between the nodes in this Euclid-
ean space, the node vectors are exactly separated by
ECTD. L
+
can therefore be considered as a similar-
ity matrix between the nodes (as in the vectors space
model in information retrieval).
In summary, three basic quantities will be used as
providing a dissimilarity/similarity measure between
nodes: the average first-passage time, the average
commute time, and the pseudoinverse of the Lapla-
cian matrix.
4 EXPERIMENTAL
METHODOLOGY
Remember that each agent of the three sets corre-
sponds to a node of the graph. Each node of the
user-agent set is connected by an edge to the watched
movies of the movie-agent set. In all these experi-
ments we do not take the movie-category agent set
into account in order to perform fair comparisons be-
tween the different methods. Indeed, two scoring
algorithms (i.e., cosine and nearest-neighbours algo-
rithms) cannot naturally use the movie-category set to
rank the movies.
4.1 Data set
For these experiments, we developed a MAS archi-
tecture corresponding to our movie example. The
belief set of the user agents, movie agents, and
movie-category agents has been instantiated from the
real MovieLens database (www.movielens.umn.edu).
Each week hundreds of users visit MovieLens to rate
and receive recommendations for movies.
We used a sample of this database proposed in
(Sarwar et al., 2002). Enough users were randomly
selected to obtain 100,000 ratings (considering only
users that had rated 20 or more movies). The data-
base was then divided into a training set and
a test set (which contains 10 ratings for each of
943 users). The training set set was converted
into a 2625 x 2625 matrix (943 user agents, and 1682
movie agents that were rated by at least one of the
user agents). The results shown here do not take into
account of the ratings provided by the user agents
here (the experiments using the ratings gave similar
results) but only the fact that a user agent has or has
not interacted with a movie agent (i.e., the user-movie
matrix is filled in with 0’s or 1’s).
We then applied the methods described in Section
4.2 to the training set and compared the results
thanks to the test set.
4.2 Scoring algorithms
Each method supplies, for each user agent, a set
of similarities (called scores) indicating preferences
about the movies, as computed by the method. Tech-
nically, these scores are derived from the computa-
tion of dissimilarities between the user-agent nodes
and the movie-agent nodes. The movie agents that are
closest to an user agent, in terms of this dissimilarity
score, (and that have not been watched) are consid-
ered the most relevant.
The first four scoring algorithms are based on the
average first-passage time and are computed from
WEB RECOMMENDATION SYSTEM BASED ON A MARKOV-CHAINMODEL
59

the probability transition matrix of the corresponding
Markov model.
Average commute time (CT). We use the average
commute time, n(i, j) , to rank the agents of the con-
sidered set, where i is an agent of the user-agent set
and j is an agent of the set to which we compute the
dissimilarity (the movie-agent set). For instance, if
we want to suggest movies to people for watching,
we will compute the average commute time between
user agents and movie agents. The lower the value
is, the more similar the two agents are. In the sequel,
this quantity will simply be referred to as “commute
time”.
Principal components analysis defined on aver-
age commute times (PCA CT). In a related paper,
we showed that, based on the eigenvector decomposi-
tion, the nodes vectors, e
i
, can be mapped into a new
Euclidean space (with 2625 dimensions in this case)
that preserves the Euclidean Commute Time Distance
(ECTD), or a m−dimensional subspace keeping as
much variance as possible, in terms of ECTD. We
varied the dimension of the subspace, m, from 25 to
2625 by step of 25. It shows the percentage of vari-
ance accounted for by the m first principal compo-
nents
P
m
i=1
λ
i
/
P
n
j=1
λ
j
. After performing a PCA
and keeping a given number of principal components,
we recompute the distances in this reduced subspace.
These Euclidean commute time distances between
user agents and movie agents are then used in order
to rank the movies for each user agent (the closest
first). The best results were obtained for 100 dimen-
sions (m = 100).
Notice that, in the related paper, we also shows that
this decomposition is similar to principal components
analysis in the sense that the projection has maximal
variance among all the possible candidate projections.
Average first-passage time (one-way). In a simi-
lar way, we use the average first-passage time, m(i|j),
to rank agent i of a the movie-agent set with respect
to agent j of the user-agent set. This provides a dis-
similarity between agent j and any agent i of the con-
sidered set. This quantity will simply be referred to as
“one-way time”.
Average first-passage time (return). As a dis-
similarity between agent j of the user-agent set and
agent i of the movie-agent set, we now use m(j|i) (the
transpose of m(i|j)), that is, the average time used to
reach j (from the user-agent set) when starting from
i. This quantity will simply be referred to as “return
time”.
We now introduce other standard collaborative fil-
tering methods to which we will compare our algo-
rithms based on first-passage time.
Nearest neighbours (KNN). The nearest neigh-
bours method is one of the simplest and oldest meth-
ods for performing general classification tasks. It can
be represented by the following rule: to classify an
Table 1: Contingency table.
Individual j
1 0 Totals
Individual i 1 a b a + b
0
c d c + d
Totals a + c b + d p = a + b + c + d
unknown pattern, choose the class of the nearest ex-
ample in the training set as measured by a similar-
ity metric. When choosing the k-nearest examples
to classify the unknown pattern, one speaks about k-
nearest neighbours techniques.
Using a nearest neighbours technique requires a
measure of “closeness”, or “similarity”. There is
often a great deal of subjectivity involved in the
choice of a similarity measure (Johnson and Wichern,
2002). Important considerations include the nature of
the variables (discrete, continuous, binary), scales of
measurement (nominal, ordinal, interval, ratio), and
subject matter knowledge.
In the case of our MAS movie architecture, pairs of
agents are compared on the basis of the presence or
absence of certain features. Similar agents have more
features in common than do dissimilar agents. The
presence or absence of a feature is described mathe-
matically by using a binary variable, which assumes
the value 1 if the feature is present (if the person i has
watched the movie k, that is if the user agent i has an
interaction with movie agent k) and the value 0 if the
feature is absent (if the person i has not watched the
movie k, that is if the user agent i has no interaction
with movie agent k).
More precisely, each agent i is characterized by
a binary vector, v
i
, encoding the interactions with
the movie agents (remember that there is an interac-
tion between an user agent and a movie agent if the
considered user has watched the considered movie).
The nearest neighbours of agent i are computed by
taking the k nearest v
j
according to a given simi-
larity measure between binary vectors, sim(i, j) =
sim(v
i
, v
j
). We performed systematic comparisons
between eight different such measures (see (Johnson
and Wichern, 2002), p.674). Based on these compar-
isons, we retained the measure that provide the best
results: a/(b + c), where a, b, c and d are defined in
Table 1. In this table, a represents the frequency of
1-1 matches between v
i
and v
j
, b is the frequency of
1-0 matches, and so forth.
We also varied systematically the number of neigh-
bours k (= 10, 20, ..., 940) . The best score was ob-
tained with 110 neighbours.
In Section 5, we only present the results ob-
tained by the best k-nearest neighbours model (i.e.,
ICEIS 2005 - SOFTWARE AGENTS AND INTERNET COMPUTING
60

sim(i, j) = a/(b + c) and k = 110).
Once the k-nearest neighbours are computed, the
movie agents that are proposed to user agent i are
those that have the highest predicted values. The pre-
dicted value of user agent i for movie agent j is com-
puted as a sum weighted by sim of the values (0 or 1)
of item j for the neighbours of user agent i:
pred(i, j) =
X
k
p=1
sim(i, p) a
pj
X
k
p=1
sim(i, p)
(5)
where a
pj
is defined in Equation 1 and we keep only
the k nearest neighbours.
Cosine coefficient. The cosine coefficient be-
tween user agents i and j , which measures the
strength and the direction of a linear relationship
between two variables, is defined by sim(i, j) =
(v
i
T
v
j
)/(kv
i
k kv
j
k).
The predicted value of user agent i for movie agent
j, considering 60 neighbours (i.e., k = 60), is com-
puted in a similar way as in the k-nearest neighbours
method (see Equation 5).
Dunham overviews in (Dunham, 2003) other simi-
larity measures related to cosine coefficient (i.e., Dice
similarity, Jaccard similarity and Overlap similarity).
In Section 5, we only show the results for the cosine
coefficient, the other methods giving very close re-
sults.
Katz. This similarity index has been proposed in
the social sciences field. In his attempt to find a new
social status index for evaluating status in a manner
free from the deficiencies of popularity contest pro-
cedures, Katz proposed in (Katz, 1953) a method of
computing similarities, taking into account not only
the number of direct links between items but, also,
the number of indirect links (going through interme-
diaries) between items.
The similarity matrix is
T = αA+α
2
A
2
+...+α
k
A
k
+... = (I−αA)
−1
−I
where A is the adjacency matrix and α is a constant
which has the force of a probability of effectiveness
of a single link. A k-step chain or path, then, has
probability α
k
of being effective. In this sense, α ac-
tually measures the non-attenuation in a link, α = 0
corresponding to complete attenuation and α = 1 to
absence of any attenuation. For the series to be con-
vergent, α must be less than the inverse of the spectral
radius of A.
For the experiment, we varied systematically the
value of α and we only present the results obtained by
the best model (i.e., α = 0.01 * (spectral radius)
−1
).
Once we have computed the similarity matrix, the
closest movie agent representing a movie that has not
been watched is proposed first to the user agent.
Dijkstra’s algorithm. Dijkstra’s algorithm solves
a shortest path problem for a directed and connected
graph which has nonnegative edge weights. As a dis-
tance between two agents of theMAS architecture, we
compute the shortest path between these two agents.
The closest movie agent representing a movie that has
not been watched is proposed first to the user agent.
Pseudoinverse of the Laplacian matrix (L
+
).
The pseudoinverse of the Laplacian matrix provides
a similarity measure since L
+
is the matrix contain-
ing the inner product of the vectors in the transformed
space where the nodes are exactly separated by the
ECTD (details are provided in a related paper). The
predicted value of user agent i for movie agent j,
considering 100 neighbours (i.e., k = 100), is com-
puted in a similar way as in the k-nearest neighbours
method (see Equation 5).
4.3 Performance evaluation
The performances of the scoring algorithms will be
assessed by a variant of Somers’D, the degree of
agreement (Siegel and Castellan, 1988).
For computing this degree of agreement, we con-
sider each possible pair of movie agents and deter-
mine if our method ranks the two agents of each
pair in the correct order (in comparison with the
test set which contains watched movies that
should be ranked first) or not. The degree of agree-
ment is therefore the proportion of pairs ranked in the
correct order with respect to the total number of pairs,
without considering those for which there is no pref-
erence. A degree of agreement of 0.5 (50% of all the
pairs are in correct order and 50% are in bad order) is
similar to a completely random ranking. On the other
hand, a degree of agreement of 1 means that the pro-
posed ranking is identical to the ideal ranking.
5 RESULTS
5.1 Ranking procedure
For each user agent, we first select the movie agents
representing movies that have not been watched.
Then, we rank them according to one of the proposed
scoring algorithms. Finally, we compare the proposed
ranking with the test set (if the ranking proce-
dure performs well, we expect watched movies be-
longing to the test set to be on top of the list) by
using the degree of agreement.
5.2 Results and discussions
The results of the comparison are tabulated in Table
2 (where we display the degree of agreement for each
WEB RECOMMENDATION SYSTEM BASED ON A MARKOV-CHAINMODEL
61
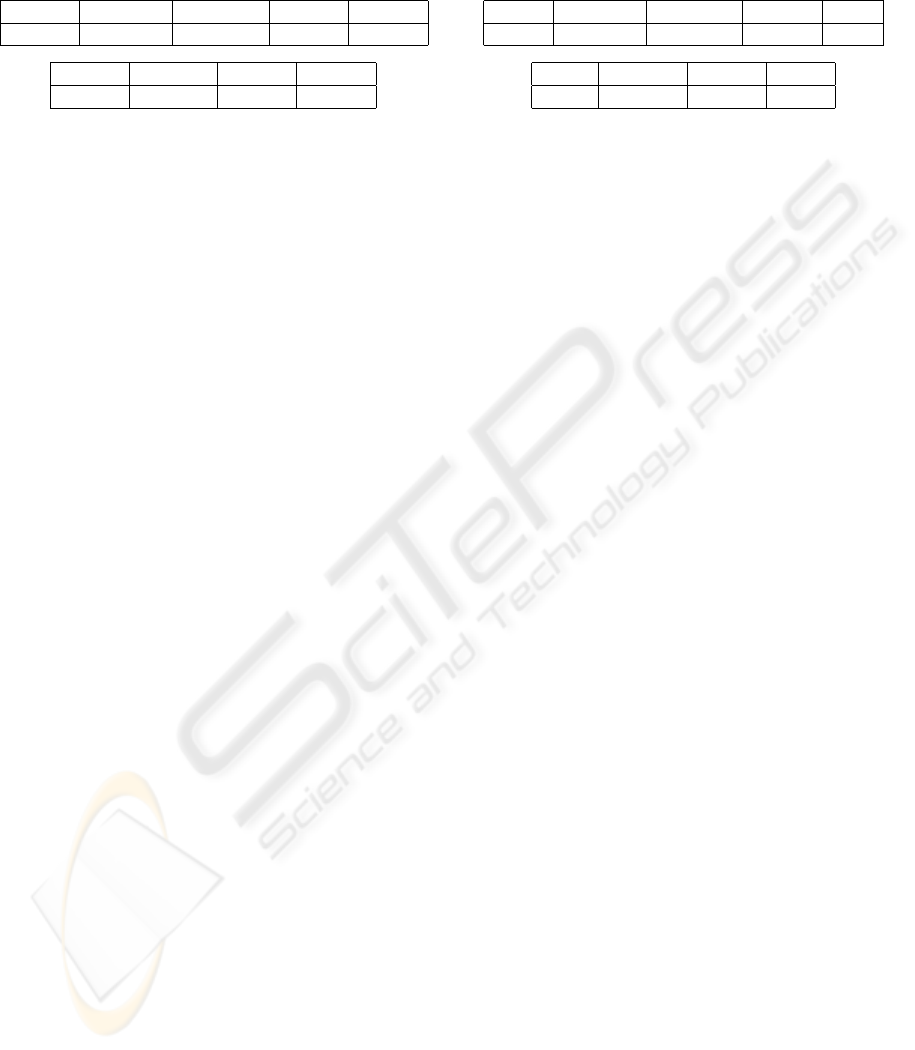
Table 2: Results obtained by the ranking procedures without
considering the movie-category set.
CT PCA CT One-way Return Katz
0.8566 0.8710 0.8564 0.8065 0.8790
KNN Dijkstra Cosine L
+
0.9266 0.5034 0.9273 0.9302
method). We used thetest set (which includes
10 movies for each of the 943 users) to compute the
global degree of agreement.
Based on Table 2, we observe that the best degree
of agreement is obtained by the L
+
method (0.9302).
The next degrees of agreement are obtained by the
Cosine (0.9273) and the k-nearest neighbours method
(0.9266). It is also observed that the commute time
and the average first-passage time (one-way) provide
good results too, but are outperformed by the Co-
sine, the KNN, Katz’ algorithm (0.8790), and the
PCA (0, 8710). They present a degree of agreement of
0.8566 and 0.8564 respectively. Notice, however, that
the results of the L
+
method, the Cosine, the KNN,
and the PCA are purely indicative, since they highly
depend on the appropriate number of neighbours or
on the appropriate number of principal components,
which are difficult to estimate a priori. The com-
mute time and the average first-passage time (one-
way) outperform the average first-passage time (re-
turn) (0.8065). A method provides much worse re-
sults: Dijkstra’s algorithm (0.5034). It seems that, for
Dijkstra algorithm, nearly each movie agent can be
reached from any user agent with a shortest path dis-
tance of 3. The degree of agreement is therefore close
to 0.5 because of the difficulty to rank the movies
agent.
5.3 Computational issues
In this section, we perform a comparison of the com-
puting times (for a Pentium 4, 2.40 GHz) for all the
implemented methods: the average commute time,
the principal components analysis (we consider 10
components), the average first-passage time one-way
and return, the Katz method, the k-nearest neigh-
bours (we consider 10 neighbours), the Dijkstra al-
gorithm, the Cosine method (we consider again 10
neighbours), and the L
+
method. Table 3 shows the
times, in seconds (using the Matlab cputime func-
tion), needed by each method to provide predictions
for all the non-watched movies agent and for each
user agent (i.e., 943 user agents).
We observe on the one hand, that the fastest method
is the k-nearest neighbours method and one the other
Table 3: Time (in sec) needed to compute predictions for all
the non-watched movies and all the users
CT PCA CT One-way Return Katz
463.9 2173.5 464.9 466.19 66.9
KNN Dijkstra Cosine L
+
19.6 5606.1 348.46 621.9
hand, that the slowest methods are PCA and Dijkstra
algorithm. The method which provides the best de-
gree of agreement (i.e., using the L
+
matrix as sim-
ilarity measure) takes much more time than the k-
nearest neighbours method but is quite as fast as the
Markov-based algorithms.
6 CONCLUSIONS AND FURTHER
WORK
We introduced a general procedure for computing dis-
similarities between agents of a MAS architecture. It
is based on a particular Markov-chain model of ran-
dom walk through the graph. More precisely, we
compute quantities (average first-passage time, av-
erage commute time, and the pseudoinverse of the
Laplacian matrix) that provide dissimilarity measures
between any pair of agents in the system.
We showed through experiments performed on
MAS architecture instantiated from the MovieLens
database that these quantities perform well in com-
parison with standard methods. In fact, as already
stressed by (Klein and Randic, 1993), the introduced
quantities provide a very general mechanism for com-
puting similarities between nodes of a graph, by ex-
ploiting its structure.
We are now investigating ways to improve the
Markov-chain based methods.
The main drawback of these methods is that it does
not scale well for large MAS. Indeed, the Markov
model has as many states as agents in the MAS. Thus,
in the case of large MAS, we should rely on the
sparseness of the data matrix as well as on iterative
formulae (such as Equation 4).
REFERENCES
Breese, J., Heckerman, D., and Kadie, C. (1998). Empiri-
cal analysis of predictive algorithms for collaborative
filtering. Proceedings of the 14th Conference on Un-
certainty in Artificial Intelligence.
ICEIS 2005 - SOFTWARE AGENTS AND INTERNET COMPUTING
62

Bremaud, P. (1999). Markov Chains: Gibbs Fields, Monte
Carlo Simulation, and Queues. Springer-Verlag.
Buckley, F. and Harary, F. (1990). Distance in graphs.
Addison-Wesley Publishing Company.
Chung, F. R. (1997). Spectral Graph Theory. American
Mathematical Society.
Dunham, M. (2003). Data Mining: Introductory and Ad-
vanced Topics. Prentice Hall.
Gobel, F. and Jagers, A. (1974). Random walks on graphs.
Stochastic Processes and their Applications, 2:311–
336.
Johnson, R. and Wichern, D. (2002). Applied Multivariate
Statistical Analysis, 5th Ed. Prentice Hall.
Katz, L. (1953). A new status index derived from sociomet-
ric analysis. Psychmetrika, 18(1):39–43.
Kemeny, J. G. and Snell, J. L. (1976). Finite Markov
Chains. Springer-Verlag.
Klein, D. J. and Randic, M. (1993). Resistance distance.
Journal of Mathematical Chemistry, 12:81–95.
Konstan, J., Miller, B., Maltz, D., Herlocker, J., Gordon, L.,
and Riedl, J. (1997). Grouplens: Applying collabora-
tive filtering to usenet news. Communications of the
ACM, 40(3):77–87.
Norris, J. (1997). Markov Chains. Cambridge University
Press.
Resnick, P., Neophytos, I., Mitesh, S., Bergstrom, P., and
Riedl, J. (1994). Grouplens: An open architecture
for collaborative filtering of netnews. Proceedings of
the Conference on Computer Supported Cooperative
Work, pages 175–186.
Sarwar, B., Karypis, G., Konstan, J., and Riedl, J. (2001).
Item-based collaborative filtering recommendation al-
gorithms. Proceedings of the International World
Wide Web Conference, pages 285–295.
Sarwar, B., Karypis, G., Konstan, J., and Riedl, J. (2002).
Recommender systems for large-scale e-commerce:
Scalable neighborhood formation using clustering.
Proceedings of the Fifth International Conference on
Computer and Information Technology.
Shardanand, U. and Maes, P. (1995). Social information
filtering: Algorithms for automating ’word of mouth’.
Proceedings of the Conference on Human Factors in
Computing Systems, pages 210–217.
Siegel, S. and Castellan, J. (1988). Nonparametric Statistics
for the Behavioral Sciences, 2nd Ed. McGraw-Hill.
White, S. and Smyth, P. (2003). Algorithms for estimat-
ing relative importance in networks. Proceedings of
the ninth ACM SIGKDD International Conference on
Knowledge Discovery and Data mining, pages 266–
275.
Wooldridge, M. and Jennings, N. R. (1994). Intelligent
agents: Theory and practice. Knowledge Engineering
Review paper, 2:115–152.
WEB RECOMMENDATION SYSTEM BASED ON A MARKOV-CHAINMODEL
63
