
DESCRIPTION OF WORKFLOW PATTERNS BASED ON P/T NETS
∗
Guofu Zhou
School of Computer, Wuhan University
Wuhan University, Wuhan, 430072, China
Yanxiang He
Zhoumin Du
Keywords:
Workflow Patterns, Workflow process, P/T nets.
Abstract:
Through comparing and analyzing Aalst’s workflow patterns, we model these patterns with P/T nets without
additional elements. Based on these models, the number of Aalst’s patterns can be reduced significatively.
Moreover, the synchronic distance is also presented to specify workflow patterns.
1 INTRODUCTION
The theoretical foundation of workflow has become
a hot problem. And, Petri nets is famous for the
feature of describing the concurrent semantics with
rich analysis techniques(CY.Yuan, 1998). Therefore,
Petri nets is an ideal modelling tool of workflow
process(WfMC, 1995). In (Aalst, 1998; Aalst et al.,
2000; Aalst, 2002), Aalst presents four special kinds
of transitions, four triggers and twenty workflow pat-
terns. Although there are advantages in describing the
semantics of workflow process by such new elements,
one obvious disadvantage is there are too many ad-
ditional elements to ensure conciseness. Moreover,
not all workflow patterns provided by Aalst are nec-
essary. In this paper, we model Aalst’s workflow pat-
terns with P/T nets, and conclude not all Aalst’s work-
flow patterns are necessary. Additionally, an algebra
method is presented to specify patterns. The content
is arranged as follows: In section 2, all workflow pat-
terns are modelled by P/T nets. Then, we discuss
why some patterns are not necessary in section3; fur-
thermore, synchronic distance is presented to specify
these patterns. Finally, a conclusion is made and our
future work is introduced briefly.
2 MODELLING PATTERNS
In workflow process, workpiece, wp for short, is ma-
nipulated by activities. wp is a computerized docu-
∗
Supported by TIF of Wuhan University, P. R. China.
ment with the necessary information. wp flows among
activities and records data produced by activities. An
activity is an operation task performed by one role
on wp. Connector connects successive activities and
controls the flow direction of workflow process. Con-
nector are called workflow pattern or pattern.
What we should pay much attention to logic and
schedule rule. Logic is the framework of workflow
process and it will not change in all workflow in-
stances. Schedule rule is effected by instance data
of workflow process and is included in wp. Abstract-
ing logic from workflow process is a key step to model
pattern with P/T nets. In this paper, we actually dis-
cuss how to model logic of patterns. Aalst’s pat-
tern(Aalst, 1999) specification can be simplified if the
logic is separated from scheduling rules.
In this paper, connector is represented by P-
element(a circle or a broken line circle or ellipse). Ac-
tivity is represented by T-element(a rectangle or a bro-
ken line rectangle). The relationship between activity
and connector is represented by the directed arc.
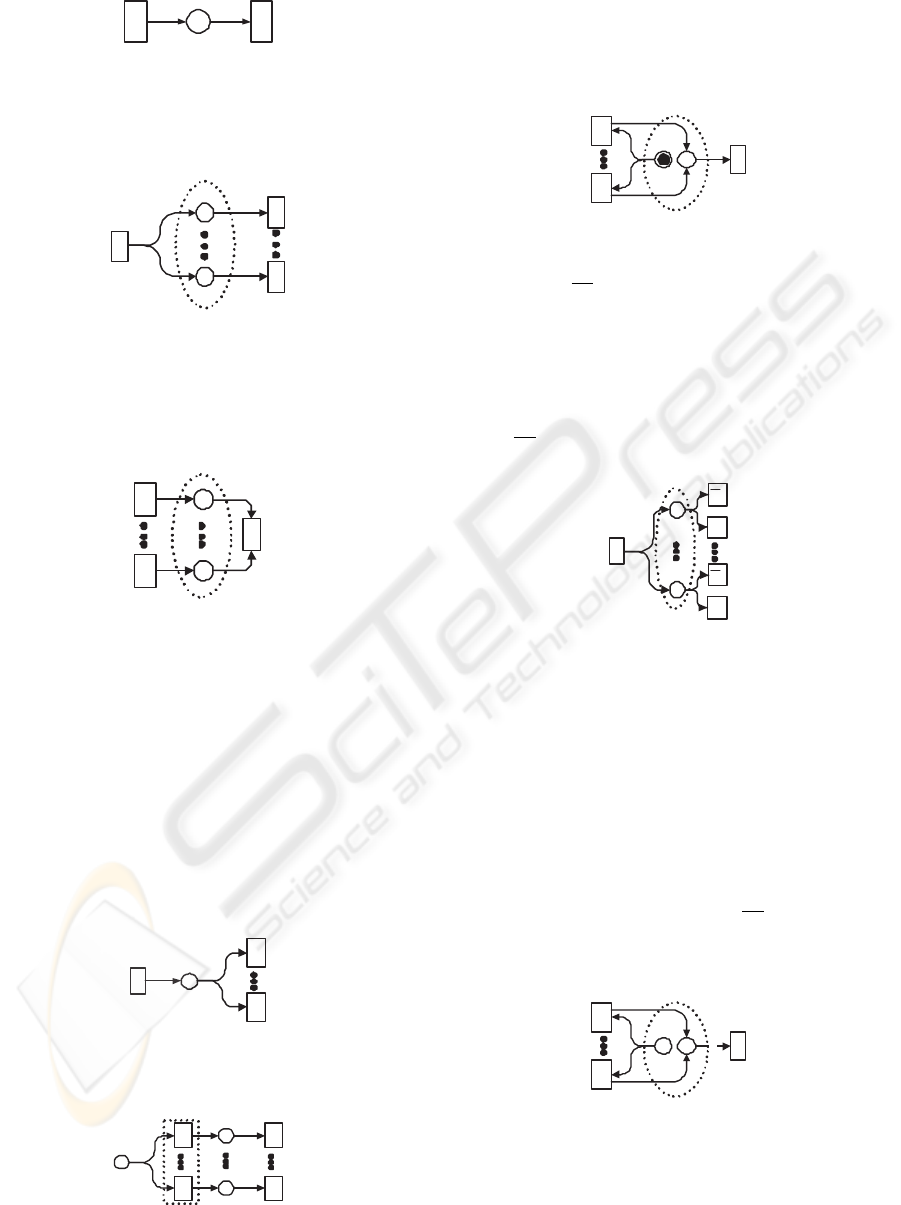
SEQUENCE is modelled as Fig.1. Where, activ-
ity A does not produce any control data. Control data
is to regulate the flow direction of workflow process.
For example, a role writes a sentence in wp: ”please
sent it to Mary”. Where, the sentence ”sent it to
Mary” is control data. For convenience, A is called
input activity and B is called output activity. AND-
Split is modelled as Fig.2. Where, activity A does
not produce any control data. The broken line el-
lipse denotes AND-Split. wp is replicated to several
copies in workflow management system, which flow
to the output activities, e.g. one copy to B and another
439
Zhou G., He Y. and Du Z. (2005).
DESCRIPTION OF WORKFLOW PATTERNS BASED ON P/T NETS.
In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 439-442
DOI: 10.5220/0002551204390442
Copyright
c
SciTePress
A B
Figure 1: SEQUENCE.
one to C. AND-Join is modelled as Fig.3. Where,
A
B
C
Figure 2: AND-Split.
A
1
· · · A
n
don’t produce any control data. Through
AND-Join, workflow management system integrates
several copies of wp into one wp. XOR-Split is mod-
A
1
A
n
C
Figure 3: AND-Join.
elled as Fig.4 or Fig.5. In Fig.4, activity A does not
produce any control data. Based on wp and related
data, XOR-Split chooses one activity from B
1
· · · B
n
to activate. So A determines which one of B
1
· · · B
n
to be activated. Specially, XOR-Split has another rep-
resentation (Fig.5). Where, activity A contains exclu-
sive subactivities A
1
· · · A
n
. Each A
i
(i = 1, · · · , n)
produces control data. Therefore, A determines to ac-
tivate which one of A
1
· · · A
n
. Because A
1
· · · A
n
are
exclusive, A
i
is activated implies B
j
will not be ac-
tivated (1 ≤ i 6= j ≤ n). XOR-Join is modelled
A
B
1
B
n
Figure 4: One case of XOR-Split.
A
1
A
n
B
1
B
n
Figure 5: Another case of XOR-Split.
as Fig.6. Where, S
1
and S
2
form a connector. The
token in S
1
determines only one of A
1
· · · A
n
can be
activated and it will flow into S
2
. C can be activated
only if S
2
has one token. OR-Split is modelled as
A
1
A
n
C
S
1
S
2
Figure 6: XOR-Join.
Fig.7. Where, B
i
denotes that activity B
i
(i = 1 · · · n)
is not be activated. When design workflow process,
we can’t know which activity will be activated. So
all possible activities must be listed, and each activ-
ity will either be activated or not. The option will be
determined by workflow management system based
on related data and control data produced by A. Ac-
tually,
B
i
can be regarded as an error output. OR-
A
B
1
B
1
B
n
B
n
Figure 7: OR-Split.
Join is modelled as Fig.8 or Fig.9. In Fig.8, x in
S
1
denotes that S
1
has x tokens, and the number of
tokens denotes the number of activities can be acti-
vated. Where, x ≤ n. Each A
i
(i = 1, · · · , n) can
be activated once and produce one token for S
2
. x in
the directed arc from S
2
to C denotes C can be acti-
vated only if S
2
has x tokens. Workflow management
system chooses activities from A
1
· · · A
n
to activate
based on wp and related data. OR-Join has another
representation (Fig.9). Where, A
1
· · · A
n
can deter-
mine whether activate B
i
or not.
B
i
denotes B
i
is
not activated and it can be regarded as an error out-
put. Multiple-Merge is modelled as Fig.10. Where,
A
1
A
n
x C
S
1
S
2
x
Figure 8: One case of OR-Join.
x tokens in S
1
denotes that x activities of A
1
· · · A
n
can be activated concurrently. The weight of directed
arc from S
2
to C is 1. If S
2
has one token, C will
be activated once. Each A
i
(i = 1 · · · n) can produce
ICEIS 2005 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION
440
A
1
B
1
B
1
B
n
B
n
Ax
A
n
Figure 9: Another case of OR-Join.
one token for S
2
, so A
1
· · · A
n
can produce x tokens
for S
2
. x tokens in S
2
implies C will be activated x
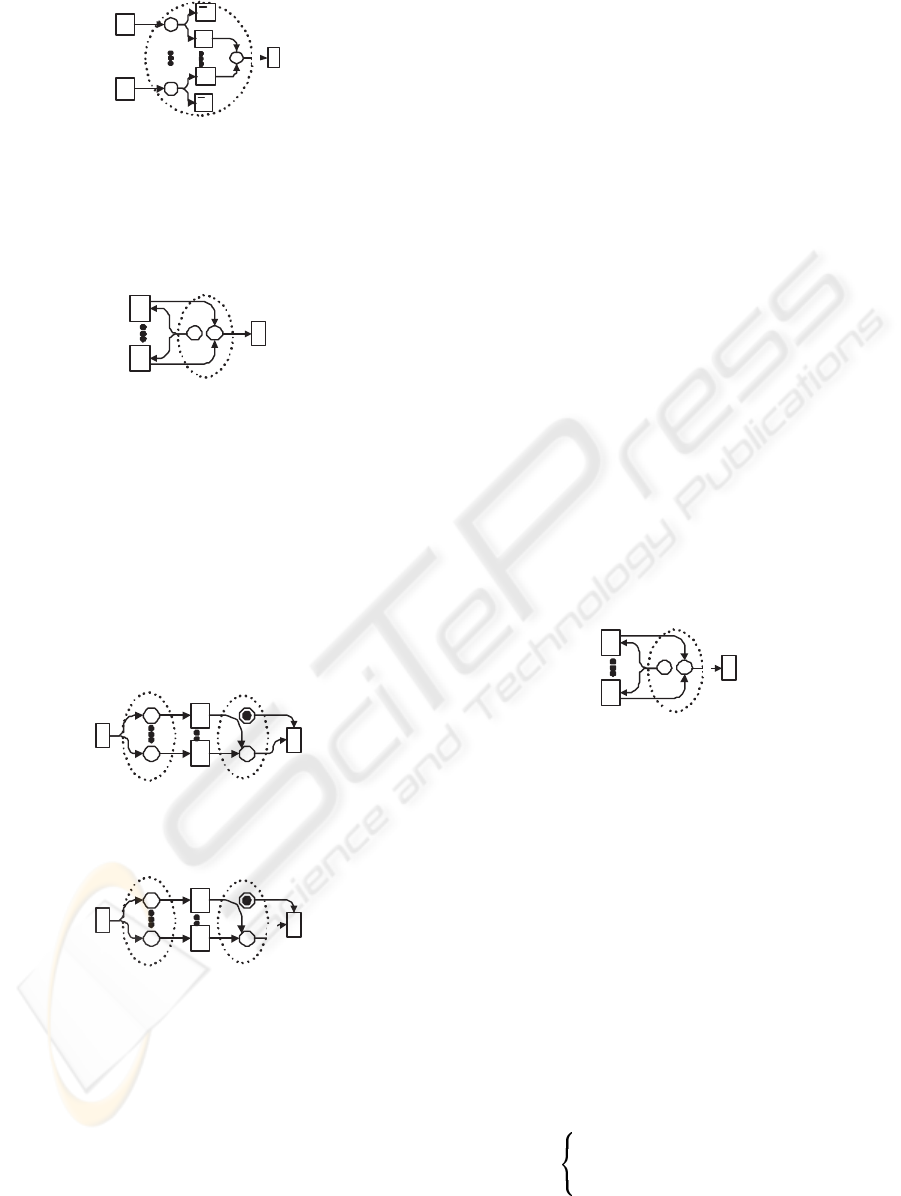
times. Discriminator is modelled as Fig.11. Where,
A
1
A
n
x C
S
1
S
2
Figure 10: Multiple-merg.
when S
1
and S
2
have one token respectively, D can
be activated and consume the tokens of both S
2
and
S
1
. Although each B
i
(i = 1 · · · m)can produce one
token for S
2
, D can’t be activated again because S
1
has no token. Actually, Discriminator is a special case
of N-out-of-M Join. In Fig.12, the weight of directed
arc from S
2
to D is n and the element number of S
2
’s
preset is m(n ≤ m). When S
2
has n tokens and S
1
has one token, D can be activated. In Discriminator,
n = 1. In(Aalst et al., 2000), Aalst also mentions
A
B
1
B
m
D
S
1
S
2
Figure 11: Discriminator.
A
B
1
B
m
D
S
1
S
2
n
Figure 12: N-out-of-M.
some other patterns. Arbitrary Cycles only modifies
wp’s content but doesn’t change the logic of workflow
process. So it can be regard as a loop. Implicit Ter-
mination denotes the process is stop. Obviously it is
not necessary to study specially. Multiple Instance
Without Synchronization, Multiple Instances With a
Priori Design Time Knowledge, Multiple Instances
With a Priori Run Time Knowledge, and Multiple In-
stances Without a Priori Run Time Knowledge are re-
lated with multiple instances, therefore they should
be discussed as process instances. Deferred Choice is
an error of resources if time is regarded as a kind of
resource. So it shall not also be considered as a pat-
tern. Interleaved Parallel Routing determine the ac-
tivating order of the concurrent activities, so this pat-
tern is similar essentially to SEQUENCE. Milestone
can activate a new activity without terminating itself,
so actually Milestone is a activity. Cancel Activity and
Cancel Case are also not patterns but error outputs.
3 PATTERN SPECIFICATION
XOR-Split is a special case of OR-Split if only one of
output activities can be activated. In XOR-Join, only
input activity is activated and output activity will be
activated only once. In OR-Join, some of input activ-
ities are activated and output activity will be activated
only once. In Multiple Merge, some of input activities
are activated and output activity will be activated cor-
responding times. Therefore, the three patterns are the
special cases of merge. In Fig.13, when m = n = 1,
merge is XOR-Join. When m = n > 1, merge is OR-
Join. When m > n = 1, merge is Multiple Merge.
When n = 1, N-out-of-M is Discriminator. There-
fore, only SEQUENCE, AND-Split, AND-Join, OR-
Split, OR-Join and N-out-of-M merge are necessary.
A
1
A
n
m C
S
1
S
2
n
Figure 13: Merge.
3.1 Specification
We specify the patterns by the algebra of Petri nets.
Let A be the set of activities and E
1
, E
2
be subsets
of A. E
1
< E
2
denotes E
1
’s activities are activated
before E
2
’s, and E1 ≤ E
2
denotes E
1
∩ E
2
6= ∅ ∧
E
1
− E
2
< E
2
− E
1
. It is called a point that wp
(and its copies) is in the hand of a role. Let p
1
, p
2
be arbitrary points. #(E
i
, p
1
, p
2
) denotes the number
of occurrences of E
i
’s activities from p
1
to p
2
(i =
0, 1, 2). p
0
is the point before the start activity.
Definition 1 Synchronic Distance
σ(E
1
, E
2
), the synchronic distance between E
1
and
E
2
, is defined as below:
σ(E
1
, E
2
) =
max
p
1
,p
2
∈P
{|#(E
1
, p
1
, p
2
)
−#(E
2
, p
1
, p
2
)|} if #E
1
= #E
2
ε if #E
1
6= #E
2
Where, P is the set of all points, and #E
i
=
max
p∈P
(#(E
i
, p
0
, p))(i = 1, 2). ε denotes no value.
DESCRIPTION OF WORKFLOW PATTERNS BASED ON P/T NETS
441

Definition 2 Asymmetric Synchronic Distance
−→
σ (E
1
, E
2
), the asymmetric synchronic distance from
E
1
to E
2
, is defined as below:
−→
σ (E
1
, E
2
) =
σ(E
1
, E
2
) if E
1
≤ E
2
ε if E
1
> E
2
Based on the above definition, we can easily get
specifications: SEQUENCE(Fig.1) is specified by
−→
σ (A, B) = 1. AND-Split(Fig.2) is specified by
−→
σ (A, B) =
−→
σ (A, C) = 1. AND-Join(Fig.3) is spec-
ified respectively by
−→
σ (A
1
, B) =
−→
σ (A
n
, C) = 1
and
−→
σ (A
1
, A
1
) = ε
Let E
3
, E
4
be multiple sets on A, i.e. E
j
: A →
{0, 1, . . .}(j = 3, 4) is a mapping from A to the set
of non-negative integers. For example, a is an ele-
ment of A and E
j
(a) is the occurrence number of a
in E
j
. To count the weighted occurrences of E
j
’s ac-
tivities, we have definitions respectively: ∗(E
j
, p) =
P
a∈E
j
E
j
(a) • #(a, p) and ∗E
j
= max
p∈P
{∗(E
j
, p)},
Where, #(a, p) = #(a, p
0
, p), E
j
(a) is the occur-
rence number of a in E
j
.
Definition 3 Weighted Synchronic Distance
σ(E
3
, E
4
) =
max
p∈P
{| ∗ (E
3
, p) − ∗(E
4
, p)|}
if ∗E
1
= ∗E
2
ε if ∗E
1
6= ∗E
2
Definition 4 Weighted Asymmetric Synchronic Dis-
tance
−→
σ (E
3
, E
4
) =
σ(E
3
, E
4
) if E
′
3
≤ ∗E
′
4
ε if E
′
3
> ∗E
′
4
Where E
′
j
= {a|a ∈ A ∧ E
j
(a) 6= 0}, j = 3, 4. For
conciseness, there are:
−→
σ (E
3
, E
4
) =
−→
σ (a, E
4
) if E
3
= {a}
−→
σ (E
3
, b) if E
4
= {b}
−→
σ (a, b) if E
3
= {a} and E
4
= {b}
For example, the pattern in Fig.14 can be specified
a OR
b
1
b
m
bOR
a
1
a
m
b
2
a
2
Figure 14: Pattern OR.
by∃n :
−→
σ (n•a, {b
1
, b
2
, · · · , b
m
}) = n∧
−→
σ (b
i
, b
j
) =
ε(i 6= j) and ∃n :
−→
σ ({a
1
, a
2
, · · · , a
m
}, n • b) =
n ∧
−→
σ (a
i
, a
j
) = ε(i 6= j). Where, 0 < n ≤ m, n • a
denotes the number of a, and n is called OR-number.
When n = 1, the pattern is XOR (exclusive OR).
OR-number may be given at any time. The specifica-
tion of pattern OR implies synchronization, including
synchronized multi-choice and synchronized multi-
merge. If not requiring synchronization, i.e. each
a
i
(i = 1, · · · , m) will activate b once, pattern OR can
be specified by ∃n :
−→
σ ({a
1
, a
2
, · · · , a
m
}, b) = n
where 0 < n ≤ m. This OR-number denotes the
number of times b will be executed.
From above discussion,similar to the graphic rep-
resentation of patterns, Synchronic distance with its
extensions also captures logic of workflow process.
4 CONCLUSION
We have analyzed and modelled all Aalst’s patterns
with P/T nets. Some patterns shall not be regarded
as patterns. The significant thing is we model the
patterns without any extensions to Petri nets or trig-
gers. Furthermore, we propose synchronic distance to
specify logic of workflow process,which can not only
achieve the same effect as Aalst’s but also be more
concise and reasonable. By our standpoint, the model
of workflow process can be divided into two layers:
control flow layer and data flow layer. Control flow
layer(modelled by Petri nets) is to check the valida-
tion and feasibility of workflow process. Data flow
layer(data flow) will be described and simulated by
UniNet (GF.Zhou, 2003).
REFERENCES
Aalst, W. (1998). The application of petri nets to workflow
managemen. Journal of Circuits, Systems, and Com-
puters, 8(1):21–66.
Aalst, W. (1999). Waflan: A petri-net-based workflow
analyzer. Systems Analysis, Modelling Simulation,
35(3):345–357.
Aalst, W. (2002). Making work flow: On the applica-
tion of petri nets to business process management. In
ICATPN’02, 23rd International Conference on Appli-
cation and Theory of Petri Nets. Springer-Verlag.
Aalst, W., Hofstede, A., B.Kiepuszewski, and A.P.Barros
(2000). Advanced workflow patterns. In CoopIS2000,
7th International Conference on Cooperative Infor-
mation Systems. Springer-Verlag.
CY.Yuan (1998). Petri net theory. Electronics Publishing
House, Beijing, 1st edition.
GF.Zhou (2003). Doctor Dissertation:Research on Mod-
elling Technology of Software Architecture based on
UniNet. Beijing University, Beijing.
WfMC (1995). The workflow reference model. Techni-
cal Report TC00-1003, Workflow Management Coali-
tion.
ICEIS 2005 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION
442
