
CONCEPTUAL OPTIMISATION IN BUSINESS PROCESS
MANAGEMENT
Yves Callejas, Jean Louis Cavarero, Martine Collard
Université de Nice-Sophia Antipolis, Laboratoire I3S
2000, route des lucioles, O6903 Sophia Antipolis cedex, France
Keywords: Business process management, quality, Modelling, evaluation, simulation, optimisation, linear and non
line
ar programming, activity diagrams, resources affectation.
Abstract: To optimise business processes is a very complex task. The go
al is double: to improve productivity and
quality. The method, developed in this paper, is composed of 4 steps : the first one is the Modelling step (to
describe the business process in a very rigorous way), then a conceptual optimisation (supported by
evaluation and simulation tools) to improve the business process structure (to make it more consistent, to
normalise it), then an operational optimisation to improve the business process performing (to make it more
efficient) by providing to each operation the necessary resources and at last a global optimisation (to take
into account all the business processes of the company under study). This method is the result of three years
research achieved for the French organism “Caisses d’Allocations Familiales: CAF”. It was validated on the
business processes of the CAF, which deal with information (files and documents), but it can also be applied
on industrial business processes (dealing with products and materials).
1 INTRODUCTION
Business process optimisation is one of the major
issues of any company. The main goals are to
improve processes quality and to improve their
productivity, by increasing the number of output
flows and/or by decreasing the quantity of necessary
resources [Rolland 1996, Butler 1999, Aalst 2002,
Aler 2002, Borrajo 2001, Estin 1996, Jonkers 1999,
Jensen 2001, Krajewski 2001, Drabble 2002,
Nareyek 2001, Haslum 2000, Williamson 1994].
The method presented in this paper starts with a
previous modelling step followed by three main
steps:
- the Modelling step
makes it possible to represent
BP with a model which has the usual guarantees of
any good model: readability, normalisation,
genericity, and which induces an optimisation more
rigorous, more consistent and less hazardous.
Modelling was decided for all these reasons in order
to avoid an empirical optimisation consisting in
improving each BP from clues based on its
behaviour, by trying to find out local solutions.
- the Conceptual optimisation step
which does not
take into account resources; it is a structural and
static optimisation.
- the Operational optimisation step
which consists in
optimising the performing of the BP by taking into
account resources, which means by locating them
the best way as possible. It is a dynamic
optimisation since the goal is to optimise
performances.
- the Multi-BP optimisation step
which is used to
optimise (in the operational way) several BP
simultaneously.
2 MODELLING
Four concepts are necessary to model business
processes: operation, flow, resources and
competencies.
Operations
: an operation is a task of a business
process. Each operation can be mandatory or
optional. A mandatory operation has to be used
systematically (always), which means it is necessary
for the right performing of the BP. An optional
operation may not be used depending on the decided
options.
Flows
: A flow is a set of homogeneous elements
passing through the BP and treated by operations.
An optional flow is a flow associated to an optional
operation. Resources and Competencies
: These 2
concepts are linked. A resource is a group of persons
having the same set of competencies. A resource
possesses one or several competencies. A
233
Xu D. (2005).
THREAT-DRIVEN ARCHITECTURAL DESIGN OF SECURE INFORMATION SYSTEMS.
In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 233-239
DOI: 10.5220/0002552002330239
Copyright
c
SciTePress

competency can be associated to several resources
(N: M link). The set of resources is a partition of the
persons set.
We consider that each operation is one-competency.
The chosen model is directly inspired from the UML
activity diagrams. In order to build activity
diagrams, we can use any tool supporting UML
notations. We can choose either a full UML
environment like RATIONAL ROSE or DESCRIBE
or a graphic modelling tool like VISIO or
SMARTDRAW. DESCRIBE was finally chosen,
because it is the tool which satisfy the better these
criteria.
3 OPTIMISING
The modelling step provides a diagram of the BP (by
using the previous concepts) in order to evaluate it
(with simulation and evaluation tools) and to
optimise it in the right directions.
3.1 Collecting information
3.1.1 Indicators
Indicators are used to evaluate a BP. They are of 2
kinds: model indicators and BP indicators.
Model indicators: they are used to evaluate the
consistency of a BP independently of its finality.
They are theorical indicators (in opposition to BP
indicators). They provide an evaluation of the
diagram quality and make it possible to check that
diagrams are satisfying the norms given by the
model. In others words, to check that the conceptual
optimisation step delivers well built
diagrams. Examples of model indicators are
following:
maximum number of input and output flows in each
operation, average number of flows per operation,
number of operations, number of loops, cyclomatic
number (number of bows-number of nodes + 2),
diagram density (number of bows/maximum number
of bows), average number of operations per
competency.
BP indicators: they are used to evaluate
performances and dysfunction of a BP. Their values
are useful to determine the optimisation priorities.
The modelling step and the objectives graph (see
Fig. 2) step make it possible to find out (for a given
BP) the list of the useful indicators.
Fig. 1 shows some examples of BP indicators in a
specific BP from the CAF
.
NODES OF THE GRAPH INDICATORS FORMAT WAY TO OBTAIN
READABILITY OF DOCUMENTS I1 : SATISFACTION PER DOCUMENT VECTOR OBSERVATION
DECREASE RATE REJECT I2 : % REJECT PER OPERATION VECTOR SIMULATION
DEMATERIALISATION I3 : % DEMATERIALISATION NUMBER OBSERVATION
Figure 1: Examples of BP indicators
Improve Customer
Relationship (Root)
Decrease performing
Time of files
Increase documents
Readability I1
Decrease wrong
decisions
Decrease reject
Rates I2
Improve flows
Traffic
Better traduct
laws
Change some
Files
Increase
Performances
Improve
filters
Action 1
Action 3
Action 4
Action 5
P1+P2+P3=100%
P1*P11 is the weight of the objective “Increase performances” on the root objective
P1
P2
P3
P11
Action 1
Dematerialise
I3
Figure 2: Example of hierarchical objectives graph
ICEIS 2005 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION
234
3.1.2 Hierarchical Objectives Graph
It is necessary to build a hierarchy of optimisation
objectives and to identify precisely those which are
means compare to the others. Thus, we propose to
build a “hierarchical objectives graph” (HOG). This
kind of graph makes it possible to show clearly the
hierarchical relationships between objectives.
If the graph is well built and exhaustive, all its
leaves are the actions to perform in order to optimise
the BP. More precisely, the graph is built by
connecting (if possible) to each node (objective)
some indicators, values of which will be provided by
evaluation and simulation steps (in the example I1,
I2 and I3).
The graph is helpful to build an optimise BP because
it gives the hierarchical links between objectives and
then optimisation priorities. Each BP has its own
graph. The bows of the graph have to be valuated
(with percentages) in order to give the satisfaction
weight of an objective to another one (higher in the
hierarchy) and to guide the process optimisation.
Simulation
This step is dedicated to the study of the BP
behaviour in order to find out some of the possible
improvements (addition or deleting operations
and/or flows, detection of wrong cycles, detection of
congestion points,…). Obviously, this step requires a
simulation tool (SIMPROCESS was chosen).
The simulation step is also used to give values to
indicators, such as the reject ratio per operation
.
3.2 Building the best BP
The conceptual optimisation of a BP is achieved
from information provided by evaluation step,
simulation step and objectives graph step. The goal
is to build the best BP as possible (in regards to
norms, indicators, objectives hierarchy). It is a very
tough step (totally hand made) which requires to
take into account simultaneously a very large
number of information and a great know how. Thus,
values of some model indicators will induce creation
or suppression of some operations and/or flows,
values of some BP indicators will generate creation
of some new paths in the diagram (by validating or
deleting optional operations) or creation of new
documents, analysis of the objectives graph make it
possible to identify the parts of the BP which have to
be optimised in priority.
Conceptual optimisation is totally guided by the
objectives graph: weights are used to know priorities
and indicators are used to decide if the nodes are
easy to optimise or not. In the example, we can
decide to give a priority to the objective “decrease
the time to perform a file” if the values of I2 are too
high and if the weight of this objective in regards to
the root objective is high. In this case, we have to
(following the graph) modify some resources and
add some operations. In opposition, if the value of I1
is too low and if the weight of the objective “to
increase readability of documents” is high, then we
have to design new documents.
Actually, the conceptual optimisation of a BP is
achieved by a lot of improvements (defined in the
leaves of the graph) performed on its diagram, in
regards to the objectives graph which gives the right
directions. But the diagram’s improvement has to be
done in respect of concepts. For this reason, we have
defined the exhaustive list of generic actions (meta-
actions) which are possible to do. Each leaf of the
graph has to be obviously an instance of one meta-
action.
Examples of meta-actions: to add a new operation,
to automate partially an operation, to split an
operation (in 2 or more) to add a new flow, to merge
2 or more flows into 1, to modify a flow, to add a
new competency, to change the destination operation
of a flow
.
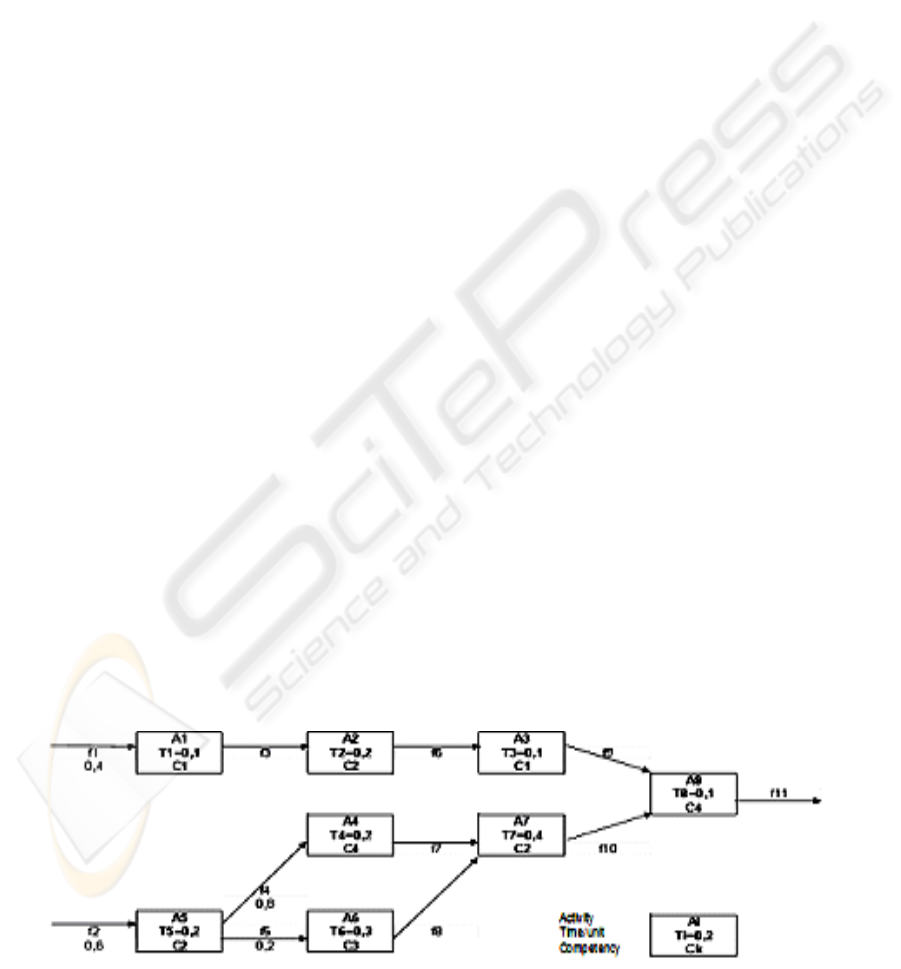
Figure 3: An example of BP
CONCEPTUAL OPTIMISATION IN BUSINESS PROCESS MANAGEMENT
235

RESOURCE COMPETENCY AVAILABILITY/
PERIOD
R1 C2 TR1=35
R2 C1, C2 TR2=35
R3 C3 TR3=35
R4 C1, C4 TR4=35
R5 C4 TR5=35
R6 C2, C3 TR6=35
R7 C2 TR7=35
R8 C2 TR8=17.5
R9 C1 TR9=17.5
Figure 4: Table resources/competencies.
FLOWS STOCKS
f1 29
f2 58
f3 6
f4 2
f5 6
f6 4
f7 4
f8 2
f9 4
f10 8
f11 0
Figure 5: Table of flows stocks.
3.3 Predicting the best affectation of
resources
This step consists in giving to each operation of a
BP, resources and competencies, in order to
maximise output flows. Actually, the final goal is to
provide a command tool to predict the best resources
affectation as possible, by taking into account
different hypothesis of degraded performing (for
example absenteeism) as well as flows stocks (flows
which have not been treated).
This third step is divided in two distinct issues:
Issue 1: Searching optimum of outputs flows (by an
optimised affectation of resources and competencies
to operations (linear optimisation).
Issue 2: Locating resources and competencies on
each operation at the right time (non linear
optimisation).
To illustrate this step, let’s take an example of BP
given in Fig. 3.
This BP is composed of 8 operations (A1, A2,.., A8)
and 9 resources (R1, R2,…, R9). The relationships
between resources and competencies are given in
Fig. 4, the stocks of flows are given in Fig. 5. Let fp
be the number of units of flow p treated and wjk be
the used time of the resource Rj for its competency
Ck (during the chosen period).
Issue 1 consists in giving resources and
competencies to each operation (by finding out
optimal values of fp and wjk) (who does what?) and
in computing the maximum number of output flow
units. The equations system to solve is following; it
corresponds to using conditions of competencies on
the period.
Competency C1 T1*f3 + T3*f9 = w21 +
w41 + w91
Competency C2 T2*f6 + T5*(f4+f5) + T7*f10 =
w12 + w22 + w62 + w72 + + w82
Competency C3 T6*f8 = w33 + w63
Competency C4 T4*f7 + T8*f11 = w44 + w54
The first legs of these equations are the total used
time of competencies. For example, competency C1
which is used in operations A1 and A3 is engaged
for a time T1*f3 in A1 and T3*f9 in A3. The second
legs correspond to the used time of competencies in
regards to resources. For example, competency C1 is
provided for a time w21 by resource R2, for a time
w41 by resource R4 and for a time w91 by resource
R9.
To solve the system we also have to take into
account two types of constraints:
Availability constraints of resources:
For each resource Rj, total used time should not be
higher than available time. There are 9 constraints of
this kind:
R1: w12 ≤ TR1 R2: w21 + w22 ≤ TR2
R3: w33 ≤ TR3 R4: w41 + w44 ≤ TR4
R5: w54 ≤ TR5 R6: w62 + w63 ≤ TR6
R7: w72 ≤ TR7 R8: w82 ≤ TR8
R9: w91 ≤ TR9
Pouring constraints on flows: Input and output flows
can be multiple. To express that input flow f2 is
approximately 60% of the total input flow (f1+f2),
we write one constraint on the flow from f1 and on
the flow from f2: f2 ≥ 1.4 * f1 and f2 ≤1.6 * f1.
To express that output flow f4 is approximately 80%
of the total output flow (f4+f5), we write one
constraint on the flow from f4 and on the flow from
f5; we write a similar constraint on the flows f7 and
f8: f4 ≥3.9 * f5 and
f4 ≤ 4.1 * f5, f7 ≥ 3.9 * f8 and f7 ≤ 4.1 * f8.
For each operation, the sum of output flows has to
be inferior to the sum of input flows: f11 ≤ f9 + f10,
f9 ≤ f6, f6 ≤ f3, f3 ≤ f1, f10 ≤ f7 + f8, f7 ≤ f4, f8 ≤
f5, f4 + f5 ≤ f2
The solver provides values of fp and wjk which
optimise output flows. The results are given in the
next tables
ICEIS 2005 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION
236
RESOURCE ∑
k
wjk AVAILABLE TIME
R1 w12 : 28 28 7
R2 w21 : 10.5 w22 : 21 31.5 3.5
R3 w33 : 17.5 17.5 17.5
R4 w41: 3.5 w44 : 31.5 35 0
R5 w54 : 21 21 14
R6 w62 : 28 w63 : 3.5 31.5 3.5
R7 w72 : 31.5 31.5 3.5
R8 w82 : 17.5 17.5 0
R9 w91 : 17.5 17.5 0
TOTAL 231 49
Figure 6: Table of competencies used time
Input flows
f1 95
f2 176
Stocks 123
Total (input + stocks) 394
Output flows (f11) 280
Non treated flows 114
Figure 7: Flows results
Figure 8: Evolution of flows
Issue 2 consists in searching dated resources
locations. (Who does what and when?). For this
reason, we have to split the period (35 hours in the
example) in 10 slices of same length D (3,5 h in the
example), and we have to find out quantities of
resources to give to each operation in each slice. The
result will be the used resources and competencies
for each slice.
For this issue, the system solving has to take into
account 3 types of constraints:
Exclusivity constraints on competencies. For each
multiple competency resource, at most one
competency is used in each slice. As we have 9
resources and 10 slices, we have 90 constraints of
this kind. If we name{Cjk}
k∈ 1..p
the set of
competencies associated to resource Rj, the
constraint may be expressed in the following way:
∀ (Resource Rj, slice t) ∃ at most one k ∈ 1..p such
that Cjk is used in slice t.
Using constraints of resources in operations. They
are equality constraints. For each slice and for each
competency, there is equality between quantities of
competencies used by operations and quantities of
competencies taken in resources. In the example,
there are four competencies and 10 slices; we have
then 40 constraints of this kind.
If we name {aik(t)}
k∈ 1..p
the set of used times of
competency Ck for the operation Ai on the slice t
and {w’jk(t)}
k∈ 1..q
the set of used times of resource
Rj for its competency Ck on the same slice, the
constraint may be expressed in the following way:
∑
i
aik(t) = ∑
j
w’jk (t) where aik(t) = αik(t) * D ;
αik(t) representing the number of times competency
Ck is used for operation Ai on the slice t (that is the
number of used resources).
Evolution constraints on flows. We assume that
flows evolve in a discontinuous way. After each
slice, flows evolve in regards to resources provided
to operations and available flows of the previous
slice. Let’s take a basic example of Fig. 8.
The formula which gives flow fb after slice t is:
Flux(b,t) = Flux(b,t-1) + Min(Flux(a,t-1),
αik(t)*D/Ti) - Min(Flux(b,t-1), αjk(t)*D/Tj) where
αik(t) represents the number of times competency
Ck is used for operation Ai on the slice t.
It is necessary to adapt this formula if operation Ai
or Aj are preceded and/or followed by several
operations.
An additional table is used to give quantities of input
flows on each slice (in regards to the chosen arrival
law)
CONCEPTUAL OPTIMISATION IN BUSINESS PROCESS MANAGEMENT
237
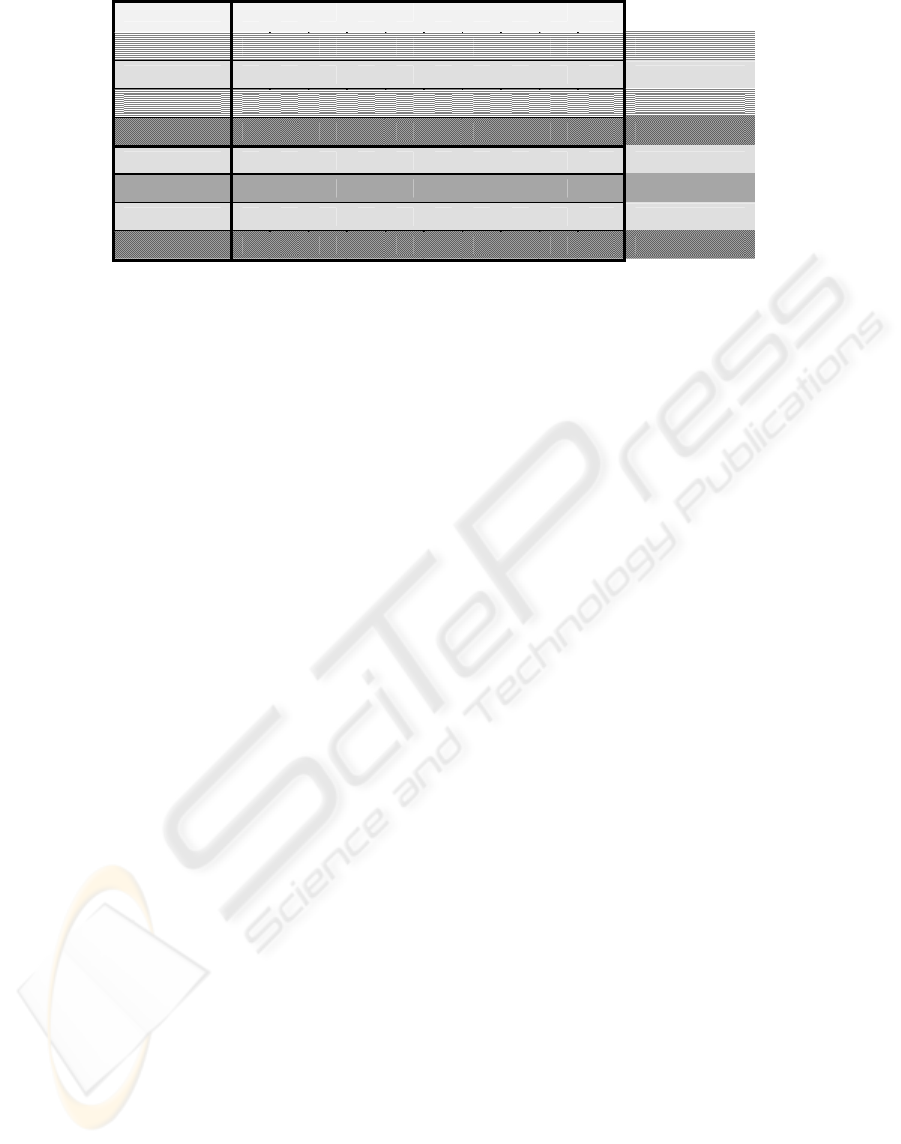
OPERATION S1 S2 S3 S4 S5 S6 S7 S8 S9 S10 COMPETENCY
A1 1 0 1 0 0 1 0 0 0 0 A1
A2 0 1 0 0 0 1 3 1 0 0 A2
A3 0 0 0 0 1 1 0 2 2 0 A3
A4 0 1 1 1 1 2 1 0 0 0 A4
A5 3 3 5 0 0 0 0 0 0 0 A5
A6 0 0 1 2 1 1 0 1 0 0 A6
A7 0 0 0 4 5 3 1 3 3 0 A7
A8 0 0 0 0 1 0 1 2 2 2 A8
Figure 9: Table of competency/operation affectation for each slice
The solver provides values of αik(t) which optimise
the repartition of resources and competencies on
each sliceand associated flows.
The table of Fig. 9 shows, the number of times αik(t)
competency Ck is used for operation Ai for the slice t. For
example, on the first slice, three resources of competency
C2 are given to operation A5 and on the fourth slice two
resources of competency C3 are given to operation A6.
4 MULTI-BP OPTIMISATION
As indicated by its name, multi-BP optimisation
consists in optimising simultaneously several BP.
Obviously, this step does not involve conceptual
optimisation (which is, by definition, made on one
BP, independently from the others) but only
operational optimisation in the case where resources
and competencies are shared by several BP. If so,
the persons in charge of the business processes have
to define priorities between BPs and constraints on
resources and competencies which will be given to
BPs and operations.
When priorities and constraints are defined, the
solver can be run (one to N times) by deleting one
by one constraints (from the bottom of the list) while
objectives are not satisfied. The multi-BP
optimisation step is, thus, a generalisation of the
operational optimisation step, using the same tool
and being done several times in a row. The final goal
is to achieve a full and global command of all the
BPs of the company
.
5 CONCLUSION
The optimisation method presented in this paper is
composed of 4 steps: Modelling step, conceptual
optimisation step, operational optimisation step,
multi-BP optimisation step. Its originality consists in
separating clearly issues related to modelling and
issues connected to optimisation. The first step
(Modelling step) is necessary to model BPs under
study and so necessary for the 3 others steps. The
second one (conceptual optimisation step) make it
possible to build the best BPs as possible, consistent
and normalised (in regards to norms, objectives and
indicators). The third one (operational optimisation)
is probably the main one. Its goal is to improve the
performances and behaviour of BPs by optimising
resources and competencies locations.
This method was validated on administrative BPs. It
also works on industrial BPs, under condition to take
into account (during the operational optimisation)
issues of breakdowns and maintenance of machines
(by using complementary tools), issues which were
not presented in this paper. This research is going to
be extended by introducing data mining techniques
in the conceptual step in order to find out more
efficient optimising rules. We would like to thank
the CNEDI 06 and more particularly M.P. Bourgeot
who made this research possible
.
REFERENCES
Aalst, W. and Hee, K.V, 2002. Workflow
Management: Models, Methods, and Systems,
ISBN : 0-262- 1189-1, MIT Press.
Aler, R. Borrajo, D. Camacho, D. and Sierra-
Alonso, A. , 2002 A knowledge-based approach
for business process reengineering, SHAMASH.
Knowledge Based Systems, 15(8):473–483.
Borrajo, D. Vegas, S. and Veloso, M., 2001. Quality
based learning for planning. In Working notes of
the IJCAI’01 Workshop on Planning with
Resources, pages 9–17, Seattle, WA (USA),
IJCAI Press.
Drabble, B. Koehler, J. and Refanidis, I. editors,
2002. Proceedings of the AIPS-02 Workshop on
Planning and Scheduling with Multiple Criteria,
Toulouse (France).
Estlin, T.A and Mooney, R.J., 1996. Multistrategy
learning of search control for partial-order
ICEIS 2005 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION
238

planning. In Proceedings of the Thirteenth
National Conference on Artificial Intelligence,
volume I, pages 843–848, Portland, Oregon.
AAAI Press/MIT Press.
Haslum, P. and Geffner, H., 2000. Admissible
heuristics for optimal planning. In Proceedings
of the Fifth International Conference on AI
Planning Systems (AIPS-2000), pages 70–82.
Jensen, P.A and Bard, J.F., 2001.
Operations
Research Models and Methods
, ISBN : 0-471-
38004-0, Wiley Higher Education
Krajewski, L. and Ritzman, P., 2001. Operations
Management: Strategy and Analysis (6th
Edition), Prentice Hall, London, 2
nd
edition.
Nareyek, A. editor, 2001. Working notes of the
IJCAI’01 Workshop on Planning with Resources,
Seattle, WA (USA), IJCAI Press.
Williamson, M and Hanks, S., 1994. Optimal
planning with a goal-directed utility model. In K.
Hammond, editor, Proceedings of the Second
International Conference on Artificial
Intelligence Planning Systems (AIPS94), pages
176–181, Chicago, Illinois
.
CONCEPTUAL OPTIMISATION IN BUSINESS PROCESS MANAGEMENT
239
