
A HYBRID CLUSTERING CRITERION FOR R*-TREE
ON BUSINESS DATA
Yaokai Feng, Zhibin Wang, Akifumi Makinouchi
The Graduate School of Information Science and Electrical Engineering, Kyushu University, Japan
Keywords: Multidimensional indices, R*-tree, clustering
criterion, Multidimensional range query, TPC-H.
Abstract: It is well-known that multidimensional indices are efficient to improve the query performance on relational
data. As one successful multi-dimensional index structure, R*-tree, a famous member of the R-tree family,
is very popular. The clustering pattern of the objects (i.e., tuples in relational tables) among R*-tree leaf
nodes is one of the deceive factors on performance of range queries, a popular kind of queries on business
data. Then, how is the clustering pattern formed? In this paper, we point out that the insert algorithm of R*-
tree, especially, its clustering criterion of choosing subtrees for new coming objects, determines the
clustering pattern of the tuples among the leaf nodes. According to our discussion and observations, it
becomes clear that the present clustering criterion of R*-tree can not lead to a good clustering pattern of
tuples when R*-tree is applied to business data, which greatly degrades query performance. After that, a
hybrid clustering criterion for the insert algorithm of R*-tree is introduced. Our discussion and experiments
indicate that query performance of R*-tree on business data is improved clearly by the hybrid criterion.
1 INTRODUCTION
More and more applications need processing
multidimensional range queries on business data
usually stored in relational tables. For example,
Relational On-Line Analytical Processing in data
warehouse is required to answer complex and
various types of range queries on large amount of
such data. In order to obtain good performance for
such multidimensional range queries, multi-
dimensional indices are helpful (V. Markl and Bayer,
1999a; V. Markl and Bayer, 1999b), in which the
tuples are clustered among the leaf nodes to restrict
the nodes to be accessed for queries.
So many index structures exist. Among them,
R*
-tree (Beckmann and Kriegel, 1990) is one of the
well-known and successful ones, and widely used in
many applications and researches (C. Chung and
Lee, 2001; D. Papadias and Delis, 1998; H.
Horinokuchi and Makinouchi, 1999; H. P. Kriegel
and Schneider, 1993; Jurgens and Lenz, 1998). R*-
tree is also used in this study. Anyway, we want to
note that our proposal in this study can also be used
to other hierarchical index structures, including the
other members of R-tree family.
In the works (C. Chung and Lee, 2001; Kotidis
and
N. Roussopoulos, 1998; Jurgens and Lenz 1998;
N. Roussopoulos and Y. Kotidis, 1997; S. Hon and
Lee, 2001), the aggregate values are pre-computed
and stored in a multidimensional index as
materialized view. When required, the aggregate
values can be retrieved efficiently. In this study, we
also use a multidimensional index for relational data.
However, it is completely different from the related
works in that our study focuses on enhancing R*-
tree to speed up evaluation of range queries
themselves.
In this paper, it is pointed out that the clustering
pat
tern of tuples among the leaf nodes is a decisive
factor on search performance. But, there exist many
very slender leaf nodes when R*-tree is used to
index business data, which greatly degrades query
performance. Slender nodes mean the nodes whose
MBRs (Minimum Bounding Rectangle) have at least
one very narrow side (even the side length is zero) in
some dimension(s). Clearly, slender nodes have very
small, even 0, areas (volumes in 3 or more
dimensional spaces. Note that, area and volume are
used interchangeably in this paper). Some examples
are those MBRs roughly shaped as line segments in
2-dimensional spaces and roughly shaped as plane or
line segments in 3-dimensional spaces.
According to our discussion in this paper, the
reaso
n of so many slender leaf nodes existing
becomes clear. The insert algorithm of R*-tree,
especially, its criterion (called clustering criterion)
346
Feng Y., Wang Z. and Makinouchi A. (2005).
A HYBRID CLUSTERING CRITERION FOR R*-TREE ON BUSINESS DATA.
In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 346-352
DOI: 10.5220/0002552703460352
Copyright
c
SciTePress
of choosing subtrees for new coming tuples,
determines the clustering pattern of tuples among the
leaf nodes. After that, we make it clear that the
present clustering criterion in the insert algorithm of
R*-tree is not suitable to R*-tree applied to business
data. Instead, a hybrid clustering criterion is
proposed. Our discussion and experiment indicate
that query performance of R*-tree on business data
is improved much by the new clustering creation.
The rest of the paper is organized as follows.
Section 2 describes how to use multidimensional
indices for relational data. Section 3 presents our
observations when R*-tree is used to business data
and the reason of our observations is discussed in
detail. Section 4 is our proposal: a hybrid clustering
criterion for R*-tree. Section 5 gives experimental
result, and Section 6 concludes the paper.
2 INDEXING BUSINESS DATA
USING R*-TREE
In this section, let us see how to use R*-tree to
business data and give some terms. Due to the
limitation of pages, R*-tree is not introduced in this
paper. Readers can refer the works (Beckmann and
Kriegel, 1990, Y. Feng, A. Makinouchi and H. Ryu,
2004).
Let T be a relational table with n attributes,
denoted by T(A1, A2, …, An). Attribute Ai (1 ≤ i ≤
n) has domain D(Ai), a set of possible values for Ai.
The attributes often have types such as Boolean,
integer, floating, character string, date, and so on.
Each tuple t in T is denoted by <a1,a2, … ,an>,
where ai (1 ≤ i ≤ n) is an element of D(Ai).
When R*-tree is used in relational tables, some
of the attributes are usually chosen as index
attributes, which are used to build R*-tree. For
simplification of description, it is supposed without
loss of generality that the first k (1≤ k ≤ n) attributes
of T, <A1,A2, … ,Ak>, are chosen as index
attributes. Since R*-tree can only deal with numeric
data, an order-preserving transformation is necessary
for each non-numeric index attributes. After
necessary transformations, the k index attributes
form a k-dimensional space, called index space,
where each tuple of T corresponds to one point.
It is not difficult to find such a mapping
function for Boolean attributes and date attributes (Y.
Feng, A. Makinouchi and H. Ryu, 2004). The work
(H. V.Jagadish and Srivastava, 2000) proposes an
efficient approach that maps character strings to real
numeric values within [0,1], where the mapping
preserves the lexicographic order. This approach is
also used in this study to deal with attributes of
character string.
We call the value range of Ai, [li, ui] (1≤ i ≤ k)
data range of Ai, an index attribute (in this paper,
“dimension” and “index attribute” are used
interchangeably). The length of the data range of Ai,
|ui-li|, is denoted by R(Ai). The k-dimensional
hyper-rectangle, [l1,u1]× [l2,u2]×…×[lk, uk], forms
the index space. Attributes specified in the range
query condition is called query attributes.
If R*-tree is used to index business data stored
in a relational table, all the tuples are clustered in
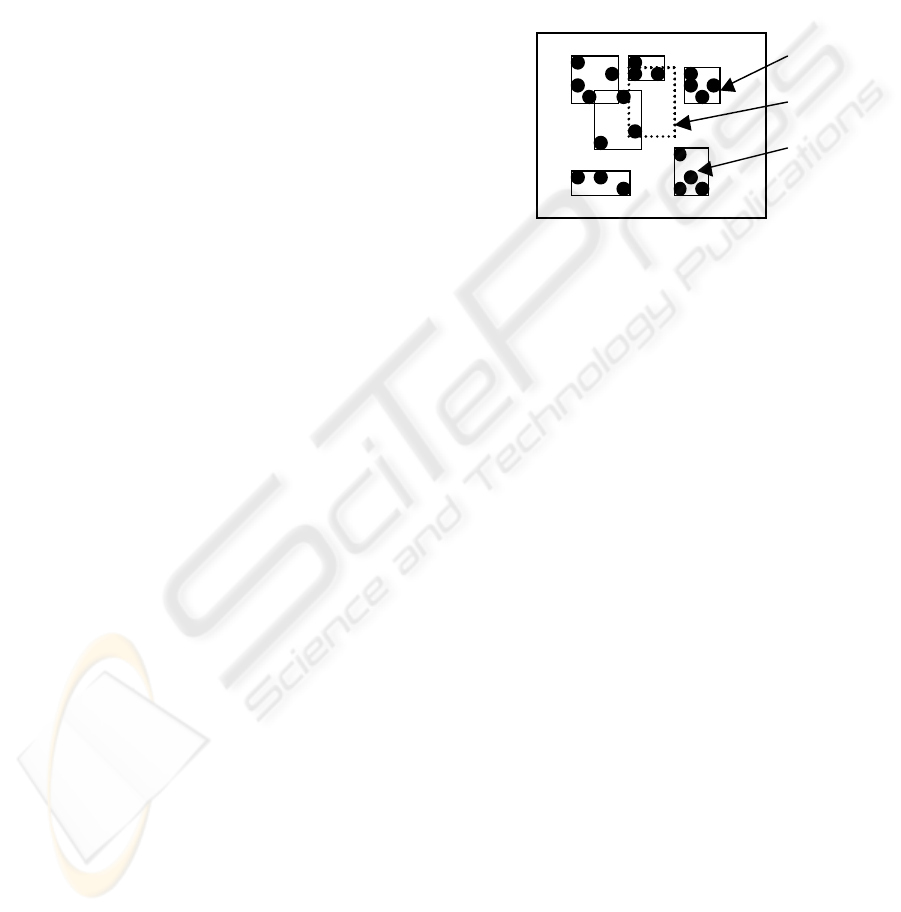
R*-tree leaf nodes. See Figure 1.
leaf nodes
query range
Figure 1. Leaf nodes and query range.
tuple
Figure 1: Leaf nodes and query range
Figure 1 shows an example of leaf nodes and query
range. Query range, given by user, refers to the
region, where the user wants to find the result.
Clearly, from Figure 1, if the tuples are properly
clustered among the leaf nodes, the number of leaf
nodes to be accessed for this range query will drop.
Thus, the clustering pattern is a deceive factor on
query performance. The question is that who decides
the clustering pattern? The answer is “clustering
criterion” in the insert algorithm of R*-tree.
R*-tree is constructed by inserting the objects
one by one. In constructing procedure, the insert
algorithm has to choose a proper subtree to contain
each new-coming tuple. The criterion that decides
which subtree should be chosen is called insert
criterion or clustering criterion in this paper. Of
course, for a given dataset, this criterion decides the
final clustering pattern of the tuples among leaf
nodes. In this paper, it will be pointed out that the
present clustering criterion of R*-tree cannot lead to
a proper clustering pattern when R*-tree is used to
business data. And a novel clustering criterion will
be proposed.
3 OBSERVATIONS AND OUR
EXPLANATION
In this section is our observations on R*-tree used
for business data. And, the observations are also
explained.
A HYBRID CLUSTERING CRITERION FOR R*-TREE ON BUSINESS DATA
347
3.1 Observations
Just as pointed out in our other work (Y. Feng, A.
Makinouchi and H. Ryu, 2004), because of the
particularity of business data, some new features
occur when R*-tree is used to index business data.
As a feature of business data, the data ranges of
attributes are very different from each other. For
instance, the data range of “Year” from 1990 to
2003 is only 13 while the amount of “Sales” for
different “Product” may be up to several hundreds of
thousands.
Another typical example of such attributes with
small cardinalities is Boolean attribute, which has
inherently only two possible values. Attributes with
other data type may also semantically have small
cardinality (e.g., “Weekday” with seven values). In
LINEITEM table of TPC-H benchmark,
RETURNFLAG, SHIPINSTRUCT, and
SHIPMODE have only 3, 4, and 7 distinct values,
respectively, although their data type is character
string.
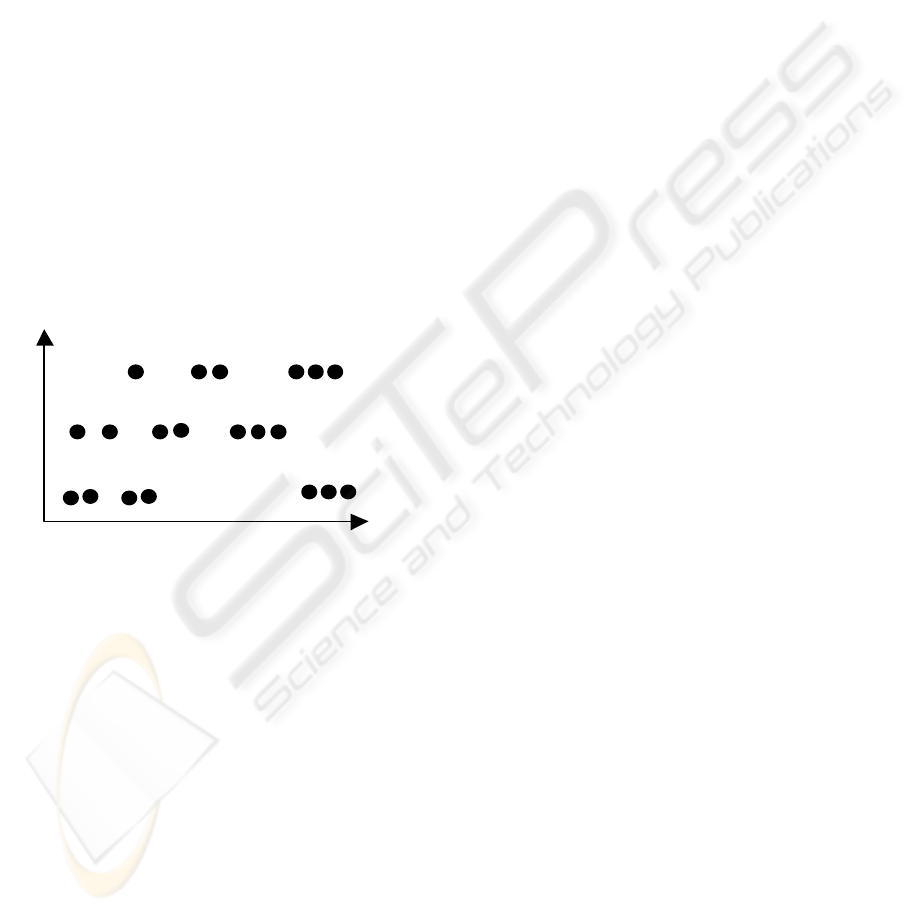
Figure 2 shows an example in 2-dimensional
space.
x-axis (floating value)
y-axis (3 values)
Figure 2. Tuples in index space.
In Figure 2, y-axis has only 3 different values. On
the contrary, x-axis type is floating and has many
possible values. Thus, the tuples (black dots) are
distributed in lines.
In order to investigate the slender nodes in R*-tree
used in business data, using the LINEITEM table in
TPC-H benchmark, an R*-tree was constructed and
all the areas (or say volumes) of the leaf nodes are
computed. Totally 200,000 tuples are generated in
this table having 16 attributes. Six attributes,
SHIPDATE (date), QUANTITY (floating),
DISCOUNT (floating), SHIPMODE (character
string), SHIP-INSTRUCT (character string), and
RETURNFLAG (character string), are selected as
index attributes since they are often used as query
attributes in the queries of the benchmark. The page
size of our system is 4KB and each leaf node can
contain at most 77 tuples. The R*-tree has 4 levels
with 4649 leaf nodes. We observe that, 2930 of these
4649 leaf nodes have 0-area. Over 60%! And, there
are still many leaf nodes have only very-small areas.
We also use 200,000 6-dimensional synthetic
data with Zipf distribution to investigate existing of
slender nodes. The observation is very similar. Zipf
distribution is often used in the researches related to
business data (S. Hong, B. Song and S. Lee. 2001).
Certainly, the basic reason that slender nodes
exist is he distribution of tuples in the index space.
3.2 The Existing Clustering Criterion
in R*-tree
Since the clustering criterion is so important on the
clustering pattern of tuples among leaf nodes of R*-
tree (which is one of deceive factors on query
performance) and this study tries to introduce a new
clustering criterion, let us briefly recall the present
clustering criterion of R*-tree as follows.
A new-coming tuple will be inserted in the
node (subtree) at the current level with
1) (for leaf level) the least enlargement of overlap
area, if tie occurs then
2) the least enlargement of MBR area, if tie occurs
again then
3) the least MBR area.
This criterion means that, if the new tuple
reaches at the leaf level, the new-coming tuple is
tried to enter each node and the enlargement of
overlap area in each case among the leaf nodes is
calculated. And the node with the least enlargement
of overlap area is chosen to contain the new-coming
tuple. If several nodes have the least enlargement
then, the enlargement of MBR area in each case is
calculated and the node with the least enlargement
of MBR area is chosen. If tie occurs again then the
node with the smallest MBR area is chosen. If tie
still occurs, then arbitrary one of those nodes with
the smallest MBR area is chosen. For the
intermediate level, the area enlargement of overlap
among the nodes is not calculated and only (2) and
(3) in the criterion are used.
Figure 2: Tuples index space
In the next subsection, we will know that the
existing of slender leaf nodes is a “positive
feedback”. That is, once some slender leaf nodes
exist, they will become more and more as the new
tuples are inserted, which greatly deteriorates search
performance.
3.3 Positive Feedback
Let us consider the insertion algorithm of R*-tree,
using the example depicted in Figure 3 (a). Node A
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
348
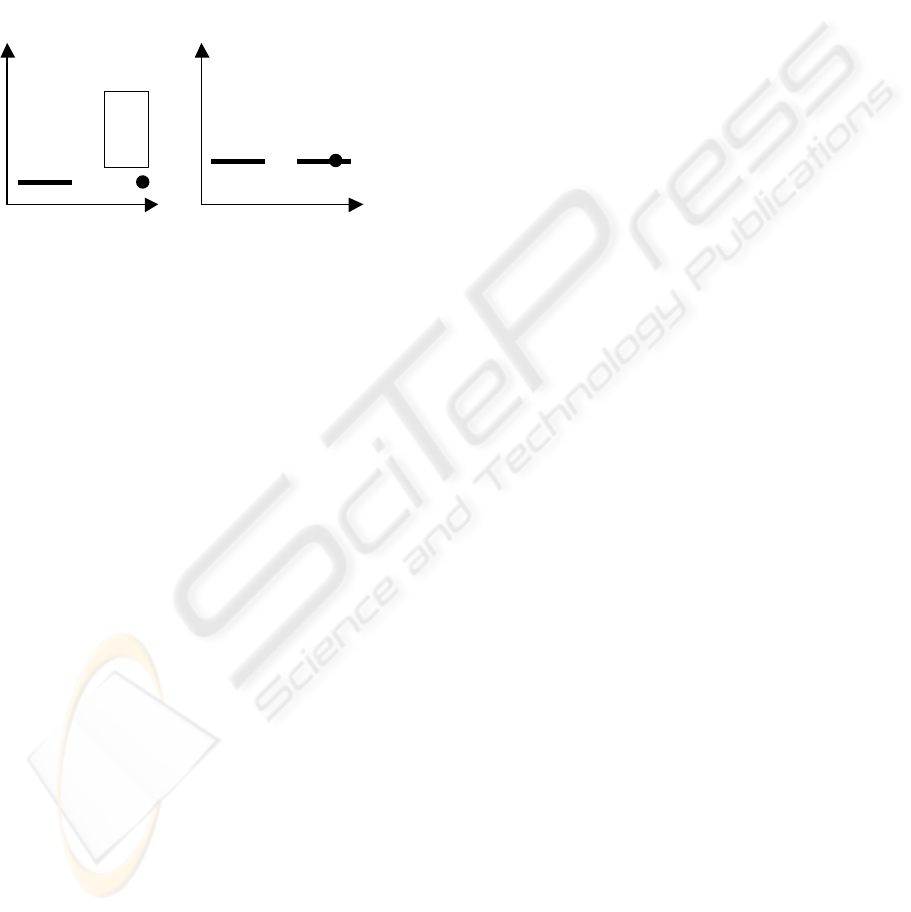
is a slender node and point p is to be newly inserted.
Certainly it should be inserted in Node B since it is
so nearer to Node B than to Node A. However,
according to the insert algorithm of R*-tree, p will
be inserted to Node A in this case. This is because
the area increment of doing so is smaller than that of
inserting p to Node B. Even if the enlargement of
overlap area among the nodes at this level is
considered, Node A also tends to be chosen. After p
is inserted Node A, Node A becomes very long,
which may deteriorate the overlap between Node A
and the other nodes.
Node A
Node B
p
Node A Node B
p
(a) (b)
Figure 3. Slender nodes exist.
Let us to see another case shown in Figure 3 (b).
There are two MBRs shaped as line segments, A and
B. Let assume p is a new tuple to be inserted. Where
should it go? Intuitively, p should be included in
Node B. Actually, p may be inserted in Node A,
although this enlarges the overlap (between A and
B) and also leads to a long node A. This is because
the insertion algorithm of R*-tree cannot determine
which node, A or B, should be selected since both
overlap area increment and area increment of
selecting A and selecting B are 0. As a result, either
Node A or Node B is selected as default without
consideration of actual overlap. Here, we assume
that without loss of generality Node A is selected.
Same as the previous case, after p is inserted Node A,
Node A becomes very long, which may deteriorate
the overlap between Node A and the other nodes.
And, when a new point (tuple) with the same y-axis
coordinate as p is inserted again, the same process is
repeated and the new point is also inserted into Node
A.
In this way, the new-coming tuples tend to be
inserted into the existing slender nodes and the
repeated insertions of such tuples lead to the
overflow of slender nodes and the slender nodes are
split again and again. As a result,
1) many slender nodes are generated,
2) the space utilization of such nodes degrades
much and the total number of nodes in R*-tree
tends to increase,
3) very slender nodes tend to be very long (there is
a low band on the number of tuples in each leaf
node),
4) overlapping among the leaf nodes is very heavy,
which greatly destroy search performance. This
study does not aim at eliminating the existing of
slender nodes since its existing, basically speaking,
is from the distribution of tuples (as mentioned
above). The main purpose of this study is to
decrease the overlap among leaf nodes by making
the clustering pattern more proper and reasonable.
At the same time, the number of slender nodes is
also decreased and the total space utilization of
nodes also can be improved.
4 A HYBRID CLUSTERING
CRITERION
Generally speaking, the present clustering criterion
(mentioned above) of R*-tree is based on area,
including overlap area enlargement, MBR area
enlargement, and MBR area, which leads to many
slender nodes and very heavy overlap among the
leaf nodes. In this section, we explain how to deal
with the problem of slender nodes by a hybrid
clustering criterion.
Figure 3: Slender nodes exist
Our approach to this problem includes the
following two points.
(1) Modifying the area calculation.
Why a proper subtree or a leaf node can not be
found for new-coming tuples? The reason is that the
enlargements both on overlap area and on MBR area
are zero for 0-area nodes. Thus, comparison can not
be made reasonably among inserting the tuples to
the existing nodes.
In order to avoid this situation, we modified the
area calculation. That is, when the area of a
rectangle, a node MBR or the overlap region of two
node MBRs, is calculated, all the zero-sides (i.e., the
side length is zero), if exist, of this rectangle is set to
a trivial non-zero positive value (e.g., 10
-4
in our
experiments).
Let us recall the original area calculation of
rectangle R as follows.
,)(
1
∏
=
=
d
i
i
SRArea
where S
i
is the side length of R in dimension i. d is
dimensionality of the index space.
In this study, this area calculation is modified as
follows.
A HYBRID CLUSTERING CRITERION FOR R*-TREE ON BUSINESS DATA
349

⎩
⎨
⎧
=−
=
′
′
=
′
∏
=
,
,0
,)(
1
otherwiseS
Svaluetrivial
S
SRaAre
i
i
i
d
i
i
where the trivial-value is set to 10
-4
in this paper.
Anyway, this trivial value must be less than the unit
in this attribute to avoid confusing. In the same time,
the trivial-value should not be too small, or the
calculation result cannot be expressed. These two
conditions are not difficult to be guaranteed in real
applications. In this way, most of un-comparable
situations caused by 0-area nodes can be avoided.
Note that, this modification only changes the
clustering pattern of tuples among the leaf nodes and
it has no effect on the correctness of the query result.
(2) Introducing a distance-criterion.
If the above area-criterion still cannot decide
which subtree or leaf node is most suitable to one
new-coming tuple, which means the area-based
clustering criterion is no longer in force, the nearest
subtree or leaf node to the new-coming tuple is
chosen.
Summarily speaking, the hybrid clustering criterion
combines the modified area-based one with a
distance-based one. The procedure is as follows.
1) For leaf level, compare the enlargements of
overlap areas using the modified calculation. If
tie then
2) Compare the enlargements of MBR areas using
the modified calculation. If tie then
3) Choose the nearest subtree (a leaf node for leaf
level).
Now, let us see how to calculate the distance from
one point to a rectangle region.
For a point p= (p
1
, …, p
d
) and a rectangle R.
Let the points s= (s
1
, …, s
d
) and t = (t
1
, …, t
d
) be the
two vertices of the node MBR with the minimum
coordinates and maximum coordinates in each axis,
respectively. The distance from p to R, dist(p, R),
can be given by
⎪
⎩
⎪
⎨
⎧
>
<
=
=
.
,
,
1
otherwisep
tpt
sps
r
where
i
iii
iii
i
i
−=
∑
,),(
2
rpRpdist
d
ii
5 EXPERIMENTS
Using the TPC-H data (Council, 1999), we
performed various experiments to show how much
the range query performance is improved using the
hybrid clustering criterion.
Dataset and index attributes: Lineitem table of
TPC-H benchmark, which has 16 attributes of
various data types including floating, integer, date,
string, Boolean. The table used in our experiments
has 200,000 tuples. Six of the total 16 attributes are
chosen as index attributes, including SHIPDATE
(date), QUANTITY (floating), DISCOUNT
(floating), SHIPMODE (character string),
SHIPINSTRUCT (character string), and
RETURNFLAG (character string), since they are
often used as query attributes in the queries of the
benchmark.
System: the page size in our system is 4KB and
all the index structures are built based on “one node
one page”.
Queries: the query ranges of QUANTITY
(floating) and DISCOUNT (floating) both are
changed from 10% to 100%. As for the date attribute
of SHIPDATE (date), the query range is the period
of one year and it is selected randomly for each
query. As for the other 3 attributes (character string),
since their numbers of possibly different values are
only 3, 4, and 7, respectively. One value is chosen
randomly in each of the 3 attributes. Each query is
repeated 100 times for different location and the
average numbers of accessed different nodes are
presented. The average number of node accesses is a
common criterion for evaluating query performance
(H. V. Jagadish and Srivastava, 2000).
5.1 Effect of the Hybrid Clustering
Criterion on R*-tree
In order to know effect of the new clustering
criterion on R*-tree itself, the total numbers of nodes
in R*-trees with different clustering criterions and
the result is present in Table 1, where M refers to the
upper bound on the number tuples contained in each
leaf node of R*-tree.
Table 1: R*-tree with different clustering criterion.
R*-tree with
original clustering
criterion
R*-tree with
hybrid clustering
criterion
M 77 77
Height 4 4
Total
number
of nodes
4892 3783
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
350

From Table 1, we can know that the hybrid
clustering criterion make R*-tree more compact.
5.2 Effect of the Hybrid Clustering
Criterion on Query Performance
Table 2: Comparison on the number of accessed different
nodes
Query
range
R*-tree with
original
clustering criterion
R*-tree with
hybrid
clustering criterion
10% 369.91 95.12
20% 648.90 126.33
30% 603.65 131.31
40% 388.67 137.30
50% 683.29 237.27
60% 489.00 248.10
70% 708.24 231.10
80% 691.89 275.48
90% 571.10 357.62
100% 764.55 358.49
The result of comparison on the number of accessed
different nodes is included in Table 2.
From Table 2, we can know that the hybrid
clustering criterion can greatly improve the query
performance. Anyway, note that,
(1) In Table 2, the first column, query range, refers
to the side length of the query range in the two
floating attributes, i.e., QUANTITY and
DISCOUNT. The query with same size of query
range in the floating attributes is repeated 100 times
with different locations (randomly). However, this
query range is not relevant to the other index
attributes, which is explained before.
(2) According to Table 2, the number of accessed
different nodes is not always increase as the “query
range” in the first column grows. This is because
that the query ranges in the other 4 index attributes
change randomly at the same time when the query
ranges in the two floating attributes grow.
Moreover, the CPU time cost is also tested and
compared, which is presented in Table 3.
From Table 3, we can observe that the hybrid
clustering criterion also lead to a shorter CPU time,
which means that it is effective even for main-
memory-resident R*-tree, where the I/O is no long
the bottleneck of the query performance. Note that,
our OS is FreeBSD 4.9 and main memory is 128MB.
Table 3: Comparison on CPU time (ms)
Query
range
R*-tree with
original
clustering criterion
R*-tree with
hybrid
clustering criterion
10% 16.401 5.939
20% 28.180 8.117
30% 26.582 8.499
40% 17.780 9.074
50% 33.137 15.817
60% 25.103 16.769
70% 33.940 15.874
80% 34.420 19.101
90% 32.721 24.772
100% 41.671 25.751
6 CONCLUSIONS
It is important to process various types of range
queries on business data. R*-tree is one of the
successful multidimensional index structures and is
also helpful to improve query performance on
business data. In this paper, we pointed out that
many slender nodes, including many 0-area nodes,
exist if R*-tree is applied to business data, which
greatly degrade query performance. The reason that
many slender nodes occur was made clear in this
paper and a hybrid clustering criterion is introduced
to deal with the problem of slender nodes.
According to our discussion, the hybrid clustering
criterion can improve the clustering pattern of tuples
among leaf nodes, especially it can decrease the
overlap among the leaf nodes. And our approach
clearly improved query performance of R*-tree in
our experiments.
ACKNOWLEDGEMENT
This research is partially supported by Japan Society
for the Promotion of Science, Grant-in-Aid for
Scientific Research 15650017 and 16200005.
REFERENCES
C. Chung, S. Chun, J. Lee, and S. Lee (2001). Dynamic
Update Cube for Range-Sum Queries. Proc. VLDB
Intl. Conf.,
Council (1999). TPC benchmark H standard specification
(decision support)".
http://www.tpc.org/tpch/
D. Papadias, N. Mamoulis, and V. Delis (1998).
Algorithms for Querying by Spatial Structure. Proc.
VLDB Intl. Conf.
A HYBRID CLUSTERING CRITERION FOR R*-TREE ON BUSINESS DATA
351

H. Horinokuchi, and A. Makinouchi (1999). Normalized
R*-tree for Spatiotemporal Databases and Its
Performance Tests. IPSJ Journal, Vol. 40, No. 3.
H. P. Kriegel, T. Brinkhoff, and R. Schneider (1993).
Efficient Spatial Query Processing in Geographic
Database Systems.
H. V. Jagadish, N.Koudas, and D. Srivastava (2000). On
Effective Multi-Dimensional Indexing for Strings.
Proc. ACM SIGMOD Intl. Conf.
J. Han and M. Kamber (2001). Data Mining—Concepts
and Techniques. Morgan Kaufmann press.
M. Jurgens, and H.-J. Lenz (1998). The Ra*-tree: An
Improved R-tree with Materialized Data for
Supporting Range Queries on OLAP-Data. Proc.
DEXA Workshop.
N. Beckmann, and H. Kriegel (1990). The R*-tree: An
Efficient and Robust Access Method for Points and
Rectangles. Proc. ACM SIGMOD Intl. Conf.
N. Roussopoulos, S.K and F. Vincent (1995). Nearest
neighbor Query. Proc. ACM SIGMOD Intl. Conf.
N. Roussopoulos, Y. K and M. Roussopoulos (1997).
Cubetree: Organizaiton of and Bulk Incremental
Updates on the Data Cube. Proc. ACM SIGMOD Intl.
Conf.
R. Agrawal, A. Gupta, and S. Sarawagi (1997).
ModelingMultidimesnional Databases. Proc. Intl. Conf.
on Data Engineering (ICDE).
S. Hon, B. Song, and S. Lee (2001). Efficient Execution of
Range-Aggregate Queries in Data Warehouse
Environments. Proc. the 20th Intl. Conf. on
conceptual modeling.
S. Hong, B. Song and S. Lee (2001). Efficient Execution
of Range-Aggregate Queries in Data Warehouse
Environments, Proc. 20th
international Conference on
CONCEPTUAL MODELING (ER 2001).
V. Markl, F. Ramsak, and R. Bayer (1999a). Improving
OLAP Performance by Multidimensional Hierarchical
Clustering. Proc. IDEAS Intl. Synposium.
V. Markl, M. Zirkel, and R. Bayer (1999b). Processing
Operations with Restrictions in Relational Database
Management Systems without external Sorting. Proc.
Intl. Conf. on Data Engineering.
Y. Feng, A. Makinouchi, and H. Ryu (2004). Improving
Query Performance on OLAP-Data Using Enhanced
Multidimensional Indices. Proc. ICEIS Intl. Conf.
Y. Kotidis, and N. Roussopoulos (1998). An Alternative
Storage Organization for ROLAP Aggregate Views
Based on Cubetrees. Proc. ACM SIGMOD Intl. Conf.
ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION
352
