A MODEL FOR POLICY BASED SERVICE COMMUNITY

Hironobu Kuruma

Systems Development Laboratory, Hitachi, Ltd.

1099 Ohzenji, Asao, Kawasaki, Japan

Shinichi Honiden

National Institute of Informatics/ The University of Tokyo

2-1-2 Hitotsubashi, Chiyoda, Tokyo, Japan

Keywords:

access control, policy of community, federation, web services.

Abstract:

Since the World Wide Web is an open system, it is difﬁcult to maintain the information about services on

the Web in a centralized server. Therefore the service mediation system could be constructed by federation of

service communities, in which each community provides and mediates limited number of services according to

its own policy. The federation should preserve the policy of each community. Furthermore, (1) scalability, (2)

veriﬁability of policy compliance, and (3) ﬂexibility to the change of federation relation should be considered

in implementing the federation. In this paper, we introduce a notion of policy of community based on access

control among players and show a community model that is aimed at specifying communications between

players compliant with policy. The community model provides function speciﬁcation of the service mediation

system. Since a meta-architecture based language is used to describe community model, communications for

the cooperation of communities can be represented separately from the communications for service request

and provision. As the result, our community model (1) represents communications between players in a

modular way, (2) provides a basis for veriﬁcation of policy compliance, and (3) encapsulates the dependencies

on partner communities.

1 INTRODUCTION

Service provision, usage, and mediation on the

web (Toyouchi et al., 2000) are becoming popular in

recent years. Since the web is an open system, there

may be much difference in the quality and trustwor-

thiness of the services. Therefore, the users have to

carefully read the agreements on usage of the service

and accept them before using these services. But it

is not easy to understand the agreement for every ser-

vice usage, and ordinary users may skip reading and

take risks of privacy loss etc., or abandon the service

usage.

A solution of this problem is to construct a com-

munity which is a gathering of players such as ser-

vice providers, users, and mediators under a policy.

In such a community, every member provides, uses,

and mediates services without agreements for each

service usage as far as their behaviours are validated

by the policy. For example, let us consider a hotel

reservation system shown in Figure1. In this system,

a customer requests the mediator to reserve a room,

and the mediator reserves a room in a suitable hotel on

behalf of the customer. If the system handles the mes-

sages only from the customers, mediator, and hotels

that agreed a certain policy, a community is formed

in which players trust the partners in the scope of the

policy. The communities may federate to construct a

larger community. Assume a ﬂight reservation sys-

tem shown in Figure2. In this system, a customer

asks the recommender the ﬂight which ﬁts his require-

ments. And then the customer request the airline com-

pany recommended by the recommender to reserve

the ﬂight. In the federation of the hotel reservation

community and the ﬂight recommendation commu-

nity, how the system is constructed so that the cus-

tomers reserve rooms as well as ﬂights? The feder-

ation should preserve the policy of each community.

Furthermore, (1) scalability, (2) veriﬁability of policy

compliance, and (3) ﬂexibility to the change of feder-

ation relation are considered in implementing it.

In this paper, we describe a model for constructing

a policy based community. Though Role-Based Ac-

cess Control (Ferraiolo et al., 2001; Ferraiolo et al.,

2003) is a powerful approach for providing security in

a community, we focus on the secutiry among com-

munities. Our objective is to (1) introduce the notions

of policy of community and policy of federation in-

360

Kuruma H. and Honiden S. (2005).

A MODEL FOR POLICY BASED SERVICE COMMUNITY.

In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 360-366

DOI: 10.5220/0002554603600366

 SciTePress

customers hotels

mediator

Figure 1: Hotel reservation service

customers

flight reservation

services

recommender

Figure 2: Flight reservation servce

dependent of the policy of each player, (2) show a

model for implementation of federation, and (3) pro-

vide a basis for construction and veriﬁcation of pol-

icy based service provision/usage/mediation systems.

The notion of the policy of community is introduced

in section 2 as an accessibility graph of player’s roles.

Based on the accessibility graph, policy preserving

federation is also deﬁned. To support the implementa-

tion of policy based federation, we introduce a com-

munity model in section 3 and show an example in

section 4. We show related work in section 5 and con-

clude our approach in section 6.

2 ACCESS POLICY

To describe accessibility of players in a community

independent of individual players, we introduce a no-

tion of the policy of community.

2.1 Agent

In this paper, we refer to entities participating in the

service provision, usage, and mediation on the web as

agents. An agent may be a computer system which

processes services automatically, or a person who

handles the requests of customers via web. In the fol-

lowing, Agn denotes the set of all agents.

2.2 Role

A role is a name of task that agents have for provi-

sion, usage, or mediation of services. Typical roles

are service provider, requester, and mediator. Let Rle

denote the set of all roles and

g : Agn → 2

Rle

be a function which relates each agent to the set of

roles it plays.

2.3 Community

A community is a set of agents playing a role in pro-

vision, usage, and mediation of services. An agent

can be a member of more than one community at the

same time. In the following, Cmm denotes the set of

all names of communities, and R

represents the set

of all roles of community which has name c ∈ Cmm.

Let A

be a community of name c ∈ Cmm :

= {x|g(x) ∩ R

6= ∅}.

We assume that an agent plays at most one role in

a community at a time. That is;

for all a ∈ Agn and c ∈ Cmm, if there exist X, Y

such that X, Y ∈ R

∧ X, Y ∈ g(a), then X = Y .

2.4 Policy of Agent

We deﬁne the policy of each agent as binary relation

of agents p ⊆ Agn × Agn. For agents x, y ∈ Agn,

(x, y) ∈ p represents that x is accessible to y.

2.5 Policy of Community

For each community c ∈ Cmm, we deﬁne the policy

of community c as binary relation p

⊆ R

× R

. The

policy of community p

represents the accessibility

relationship of roles. That is;

for all X, Y ∈ R

, X is accessible to Y if and only if

(X, Y ) ∈ p

Let p be the policy of agents and p

be the policy of

community c. For all x, y ∈ Agn, x is accessible to y

if and only if there exist X and Y such that (x, y) ∈

p ∧ X ∈ g(x) ∧ Y ∈ g(y) ∧ (X, Y ) ∈ p

2.6 Policy of Federation

A federation is a community of which roles are super-

set of roles of communities participating in the feder-

ation. In this paper, we deﬁne policy of federation as

the delegation relation of access rights between roles.

The policy of federation provides the basis for verify-

ing the preservation of communities’ policies partici-

pating in the federation.

For communities m and n participating in a fed-

eration, we deﬁne the policy of federation as a pair

⊆ R

× R

. (X, Y ) ∈ P

represents that the

rights of X to access the roles in m are delegated to

Y . That is, Y is accessible to the roles of m to which

X is accessible.

To extend the notion of policy of federation to fed-

eration of more than two communities, we introduce

A MODEL FOR POLICY BASED SERVICE COMMUNITY

361

1.broker

6.result

4.service_request

3.answer 2.recommend

5.result

requester agent provider agent

mediator agent

Figure 3: Communication for brokerage

reﬂective transitive closure P

∗

. For all pairs of com-

ponent communities m and n of a federation, P

∗

the minimal set satisfying the following.

• P

⊆ P

∗

and P

⊆ P

∗

• ∀X ∈ R

∪ R

, (X, X) ∈ P

∗

• for all roles X, Y , Z, if (X, Y ) ∈ P

∗

∧ (Y, Z) ∈

∗

then (X, Z) ∈ P

∗

2.6.1 Policy Preservation

Assume that c

, ..., c

are communities participating

in federation c. Let p

, ..., p

be the policy of each

component community and p

be the policy of com-

munity c. When p

satisﬁes the following, we say that

the policy of c preserves the policy of c

(1 ≤ i ≤ m)

under the policy of federation P

∗

• p

⊆ p

• for role Y of c

, if (X, Y ) ∈ p

then there exists X

′

such that (X

′

, X) ∈ P

∗

∧ (X

′

, Y ) ∈ p

2.7 Example

2.7.1 Policy of Community

Let A be a community of brokerage in which agents

interact as shown in Figure 3; that is

1. a requester agent requests a service to the mediator

agent

2. the mediator agent requests the service to a

provider agent

3. the mediator agent provides the requester agent for

the service on behalf of the provider agent

On the other hand, let B be a community of recom-

mendation in which agents interact as shown in Fig 4;

that is

1. a requester agent requests a service to the mediator

agent

2. the mediator agent recommends a provider agent to

the requester agent

3. the requester agent requests the service to the

provider agent

1.recommend

2.answer

3.service_request

4.result

requester agent provider agent

mediator agent

Figure 4: Communication for recommendation

Let A.R, A.M , and A.P be the roles of requester

agents, mediator angents, and provider agents of the

community A respectively. The policy of community

A is

= {(A.R, A.M), (A.M, A.P ), (A.M, A.M )}

Similarly, the policy of community B can be repre-

sented as follows, where the roles B.R, B.M and

B.P represent the role of requester, mediator and

provider agents respectively.

= {(B.R, B.M), (B.R, B.P )}

2.7.2 Policy of Federation

In the federation of A and B, let us require that B.R

has access right that A.R has to the roles of A and

A.M has access right that B.R has. The policy of

federation P

, P

and P

∗

are as follows.

= {(A.R, B.R)}, P

= {(B.R, A.M)}.

∗

= P

∪ P

∪

{(A.R, A.R), (A.M, A.M), (A.P, A.P ),

(B.R, B.R), (B.M, B.M ), (B.P, B.P )}

2.7.3 Policy Preservation

Let D be the community constructed by the federation

of A and B, and take the policy of the community D

= p

∪ p

∪

{(A.M, B.M ), (A.M, B.P ), (B.R, A.M )}

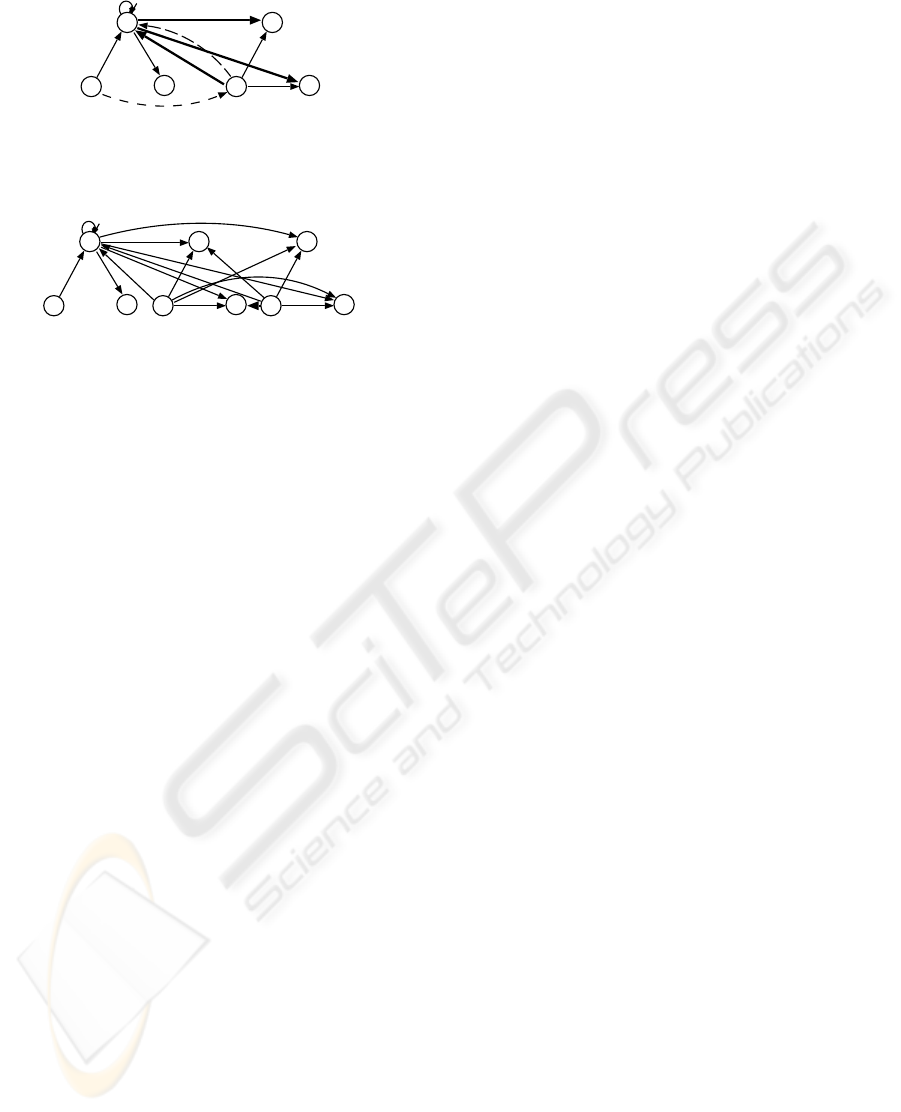
Figure 5 shows the policy of D. In this ﬁgure, the

circles represent roles and the dotted arrows represent

the policy of federation. The solid arrows represent

the policy of D. For example, an arrow from X to Y

means that (X, Y ) ∈ p

. With respect to the deﬁni-

tion in section 2.6.1, we can see that the policy of A

and B are preserved in p

2.7.4 Extension of Federation

The federation may be extended by the further feder-

ation with other communities. Let C be a community

of recommendation with the policy of community p

= {(C.R, C.M ), (C.R, C.P )}

ICEIS 2005 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

362

A.R

A.M

A.P

B.R

B.P

B.M

Community A Community B

Figure 5: Policy preservation

A.R

A.M

A.P B.R

B.P

B.M

Community A Community B

C.R

C.P

C.M

Community C

Figure 6: Policy of community extended by further federa-

tion

Assume the policy of federation;

= {(C.R, B.R), (C.R, A.M)},

F C

= {(A.R, C.R), (B.R, C.R)}.

The following policy p

of community E, which is

the federation of C and D, is a policy which pre-

servies the policies of C and D. p

also preserves

the policies of A and B.

= p

∪ p

∪ {(C.R, A.M ),

(C.R, B.M), (C.R, B.P ), (A.M, C.M),

(A.M, C.P ), (B.R, C.M ), (B.R, C.P )}

Figure 6 shows the policy of community E.

3 COMMUNITY MODEL

In the federation, the agents of each community are

required to be compliant with the policy of the com-

munity when they interact with agents of other com-

munities. Therefore, the implementation of a policy

based federation basically consists of restricting the

communications across the communities and adding

communications for cooperation of communities.

To support the implemention of the federation,

we introduce a community model which represents

the communications in federation hierachically. This

model is written in a modelling language whose syn-

tax is shown in Appendix A. The modelling lan-

guage introduces the notion of meta-hierarchy and

ﬁeld; (1) meta-level description can be attached to

specify the dynamism of agent’s behaviour, and (2)

message passing is restricted to the range of agents

which share the same ﬁeld.

3.1 Meta-level Architecture

In the modelling language, an agent is speciﬁed in

several levels. The lowest level is 0 level, which we

call the base level. Though the modelling language

does not ﬁx the number of meta-levels, let n denotes

the highest level declared in the community model.

In the syntax of Appendix A, the number of “m”s at

<DESCRIPTION ID> show the meta-level. The be-

haviour of agent, such as change of state and transmis-

sion of a message, is speciﬁed in each level.

A message transmitted in level i (0 ≤ i < n) is ma-

nipulated in level i + 1; i.e. we can control the trans-

mission of the message by explicitly specifying the

process of dequeueing, passing to the receiver agent,

and enqueing to the message queue in i + 1 level.

The invocation of method in i level is performed by

execute method of i + 1 level. Below we describe

the meaning of message invocation, where N denotes

set of natural numbers representing meta-level, M sg

denotes set of message patterns, and F ld denotes set

of ﬁelds.

Firstly, we deﬁne a function

acceptable : M sg × Agn × N → bool

which shows the existence of a method.

• if a method which ﬁts in message m is speciﬁed in

i level of agent a : acceptable(m, a, i) = true

• otherwise : acceptable(m, a, i) = false

Since any message transmitted in i level can be ma-

nipulated in i + 1 level, the message invocation by

message m in i ≤ n level is decided by the following

function

executable : M sg × Agn × N → bool.

• i = n : executable(m, a, i) = acceptable(m, a, i)

• i < n : if the invocation of execute for m

is speciﬁed or nothing is speciﬁed (default as-

sumed) in i + 1 level, executable(m, a, i) =

acceptable(m, a, i)

if the message m is rewritten to m

′

and

execute is invoked for m

′

in i + 1 level,

executable(m, a, i) = acceptable(m

′

, a, i)

otherwise : executable(m, a, i) = f alse

3.2 Message Transfer

A community model possibly contain several ﬁelds.

The message passing of agents are limited by the

ﬁelds; i.e. no message is passed from an agent to other

agents unless they stay in the same ﬁeld. However, a

message can be transferred across the ﬁelds if it is for-

warded by agents placed in more than two ﬁelds.

Consider that an agent a

in ﬁeld f

sends an i-

level message m to a

in ﬁeld f

. Due to the message

A MODEL FOR POLICY BASED SERVICE COMMUNITY

363

manipulation speciﬁed in i+1 level, this message may

be passed to other agents and executed by them. We

deﬁne the function transfer :

Msg × (Agn × F ld) × (Agn × F ld) × N → bool

which shows the transformation of the message to an

agent a in f as follows.

transfer(m, (a

, f

), (a, f), i) =

forward(wrap(m), (a

, f

), (a, f), i + 1) ∧

executable(m, a, i)

where wrap(m

) denotes the message which passes

the message m

in i + 1 level. If wrap(m

) is not

speciﬁed in i + 1 level, default method is assumed so

as to acceptable(wrap(m

), a, i + 1) = true.

The function forward :

Msg × (Agn × F ld) × (Agn × F ld) × N → bool

which shows the forwarding of message m transmit-

ted from a

in f

to a

in f

in i level, is deﬁned as

follows.

• i = n + 1

if f = f

= f

and a = a

then

forward(m, (a

, f

), (a, f), i) = true

else forward(m, (a

, f

), (a, f), i) = f alse

• 0 < i ≤ n

if there exists an agent a

which forwards m,

forward(m, (a

, f

), (a, f), i) =

forward(m, (a

, f

), (a

, f

), i) ∧

transfer(m, (a

, f

), (a, f), i)

otherwise

forward(m, (a

, f

), (a, f), i) =

transfer(m, (a

, f

), (a, f), i)

where f

and f

are ﬁelds in which a

stays, and they

may be different.

3.3 Veriﬁcation of Compliance with

Policy

The communications speciﬁed in the community

model should be compliant with the policy of the

community. This can be verifyed as follows.

Let us deﬁne a relation Acc which shows the access

between roles.

Acc = {hX, Y i|∃a, b ∈ Agn(∃u, v ∈ F ld

(∃m ∈ Msg(X ∈ g(a) ∩ R

∧ Y ∈ g(b) ∩ R

∧transfer(m, (a, u), (b, v), 0))))}

where R

and R

are the set of roles of communities

U and V respectively.

For the policy of community p

, the community

model is an implementation of p

if and only if

Acc ⊆ p

4 EXAMPLE OF COMMUNITY

MODEL

In this section, we show a community model for the

community illustrated in section 2.7.

4.1 Model of Each Community

In the community model, let A and B be ﬁelds and

place the typical agents which represent roles of com-

munities A and B in ﬁelds A and B respectively. The

communications shown in Figures 3 and 4 are per-

formed in the base-level of each agent. On the other

hand, we described the communications for coopera-

tion of communities in the meta-level of each agent as

follows.

The following are communications for cooperation

that are common in every mediator agents speciﬁed in

the 1 level.

• forward the message to the receiver agent which

shares the same ﬁeld

• forward the message to the mediator agent if the

receiver agent is not in the same ﬁeld

For the requester and provider agents in community

B, the following is speciﬁed in the 1 level to commu-

nicate agents in other community directly.

• ask the mediator agent for forwarding the message

if the receiver agent is not in the same ﬁeld

The following are speciﬁed in the 1 level of media-

tor agents in community A which behave as provider

agents when they receive request from agent in other

communities.

• manipulate the base-level message answer so as

to reply itself as a provider

• change the base-level message

service_request to broker message

4.2 Model of Federation

The community D, which is the federation of A and

B, is modelled as follows.

• add mediator agents of community A to ﬁeld B

• add mediator agents of community B to ﬁeld A

• to delegate a request to other mediator, a media-

tor which received a recommend message in base

level performs

– execute the message at base level

– if the request is satisﬁed, return answer mes-

sage

– otherwise forward the recommend message to

other mediators

ICEIS 2005 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

364

requester

of A

broker

answer

result

service_request

result

recommend

field A

field B

mediator

of A

mediator

of B

provider

of B

Figure 7: Message sequence (A to B)

recommend

answer

service_request

result

service_request

result

broker

field B

field A

requester

of B

mediator

of B

mediator

of A

provider

of A

Figure 8: Message sequence (B to A)

• change the common communication in the 1 level

of the mediator agents of A so that they reject the

message transfer from agents in other ﬁeld, if the

receiver of the message is requester or provider

agent in ﬁeld A.

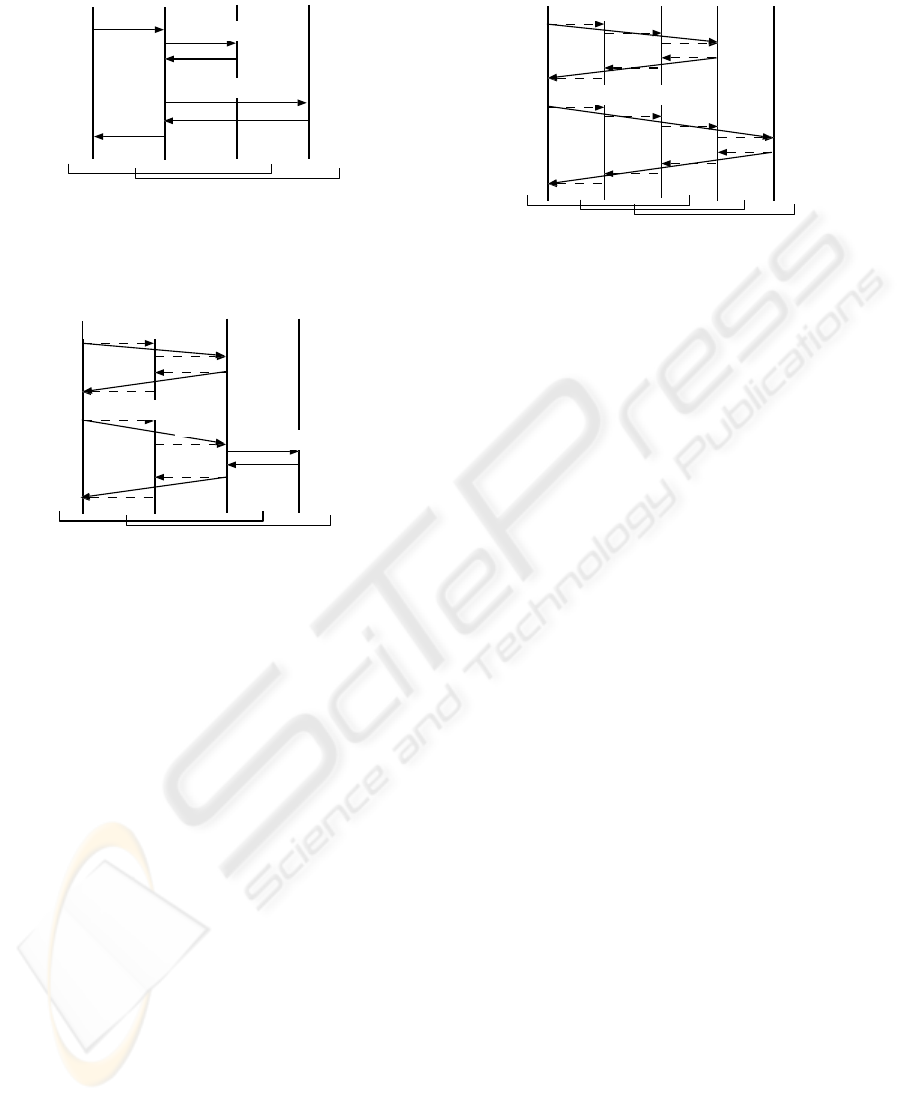
Figure 7 shows the communication of a requester

agent of A and agents in B when the requester agent

uses a service in B. Figure 8 shows the communi-

cation of requester agent of B and agents in A when

the requester agent uses a service in A. In this ﬁgure,

dotted arrows show the communication in the 1-level.

4.3 Extension of Federation

The community E, which is a federation of commu-

nities D and C, is modelled as follows.

• add mediator agents of community A to ﬁeld C

• add mediator agents of community C to ﬁeld A

• add the following behaviours to agents of C when

they receive a recommend message

– execute the message at base level.

– if the request is satisﬁed, return answer mes-

sage.

recommend

answer

service_request

result

field B

field A

field C

requester

of B

mediator

of B

mediator

of A

mediator

of C

provider

of C

Figure 9: Message sequence (B to C)

– otherwise forward the recommend message to

other mediators.

Figure 9 shows the communication of requester agent

of B and agents in C when the requester agent uses a

service in C.

5 RELATED WORK

RBAC/Web (Kuhn et al., 1997) is an implementa-

tion of Role Based Access Control for Web services.

It controls the access to the information on the Web

based on the roles assigned to the users. The concept

that operations are associated with roles simpliﬁes the

understanding and management of privileges. How-

ever, RBAC/Web does not support the federation we

described in this paper.

UDDI, Universal Description, Discovery, and Inte-

gration, is a registry for sharing information on Web

Services. It is also speciﬁcation for service descrip-

tion and discovery. In the version 3 of the speciﬁ-

cation, UDDI support the multiple registry interac-

tion and policy description for different registry im-

plementations. In our work, the policy of community

deﬁnes the accessibility relations in service provi-

sion/usage/mediation community and the community

model speciﬁes the communications between players.

Therefore the UDDI registry can be used a basis for

the implementation of communities and their federa-

tions in our work.

Many works have been done in the research domain

of meta-level programming and reﬂection (Maes,

1988; Charlton, 1996). Adaptive Software Agents be-

have reﬂectively to adapt the change of their environ-

ments. The objective of these works is principally to

program agents that adopt their environments. The

objective of our work, on the other hand, is to provide

a method for developing service mediation systems

that are ﬂexible with the change of federation rela-

A MODEL FOR POLICY BASED SERVICE COMMUNITY

365

tions. The agents in our community model provide

function speciﬁcation of a service mediation system

which is to be implemented in ordinary programming

language. In the future, agents in a community model

may be implemented on the basis of adaptive software

agents so that they autonomously adapt and observe

the policies.

6 CONCLUSION

In this paper, we introduced a notion of policy of

service community based on access control among

roles and showed a multi-level communication model

for policy implementation. Our model (1) represents

communications in a hierarchcal way, (2) provides a

basis for veriﬁcation of policy preserving communi-

cations and (3) encapsulates the dependencies on part-

ner communities.

Since the agents of our model are described in

multi-level, implementing them in ordinary program-

ming language is not an easy task. Our future work is

to develop a method for constructing service media-

tion systems from our model.

REFERENCES

Charlton, P. (1996). Self-conﬁgurable software agents. In

Advances in Object-Oriented Metalevel Architectures

and Reﬂection, pages 103–127. CRC Press.

Ferraiolo, D. F., Kuhn, D. R., and Chandramouli, R. (2003).

Role-Based Access Control. ARTECH HOUSE, Inc.

Ferraiolo, D. F., Sandhu, R., Gavrila, S., Kuhn, D. R., and

Chandramouli, R. (2001). Proposed nist standartd for

role-based access control. ACM Trans. on Information

and System Security, 4(3):224–274.

Kuhn, D., Barkley, J., Cincotta, V., Ferraiolo, D., and

Gavriella, S. (1997). Role based access control for the

world wide web. In Proc. 20th National Information

Systems Security Conference, pages 331–340.

Maes, P. (1988). Issues in computational reﬂection. In

Meta-Level Architectures and Reﬂection, pages 1–35.

Elsevier Science Publishers B.V. (North-Holland).

Toyouchi, J., Funabashi, M., and Strick, L. (2000). Service

integration platform based on tina 3-tier model and in-

terfaces. In TINA 2000 CONFERENCE Conference

Proceedings, pages 21–26.

A SYNTAX OF MODELLING

LANGUAGE

<AGENT> ::=

<DESCRIPTION> ("," <DESCRIPTION>)

<DESCRIPTION> ::=

"{" <DESCTIPTION ID> "|"

[ "attribute" <ATTRIBUTE>

("," <ATTRIBUTE>)

";;" ]

[ "method" <METHOD>

("," <METHOD>)

";;" ] "}"

<DESCRIPTION ID> ::=

agent_name

| "m(" <DESCRIPTION ID> ")"

<ATTRIBUTE> :=

variable_name ":" <TERM>

<METHOD> ::=

<MESSAGE PATTERN> ::=

message_name <TERM>

<STATEMENTES> ::=

<STATEMENT> (";" <STATEMENT>)

<STATEMENT> ::=

| <ASSIGNMENT> | <EXPRESSION>

<CONDITIONAL> ::=

"if" <EXPRESSION>

"then" "(" <STATEMENTS> ")"

[ "else" "(" <STATEMENTS> ")" ]

<CASE> ::=

"case" <EXPRESSION> "of"

(<PATTERN> ":" "(" <STATEMENTS> ")")+

["otherwise"":""("<STATEMENTS>")"]

<ASSIGNMENT> ::=

"let" <PATTERN>

<EXPRESSION> ::=

| <PATTERN EXPRESSION>

| "forall" variable_name

"with (" <EXPRESSION> ")"

| "forsome" variable_name

"with (" <EXPRESSION> ")"

<MESSAGE TRANSMISSION> ::=

<TERM> ::=

"(" <EXPRESSION> ")"

| agent_name "." field_name

| variable_name | "dequeue"

| "execute(" variable_name ")"

<PATTERN EXPRESSION> ::=

<PATTERN> ::=

<EXPRESSION> | literal

ICEIS 2005 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION

366