Generating Code for Mapping UML Associations

Into C#

Iraky H. Khalifa

, Ebada A. Sarhan

and Magdy S. A. Mahmoud

Helwan University, Computer Science Department, Faculty of Computer Science and in-

formation, Egypt

Suez Canal University, Computer Science Department, Faculty of Computer Science and

information, Ismailia, Egypt

Abstract. Object-oriented programming languages do not contain syntax or

semantics to express associations directly. Therefore, UML associations have to

be implemented by an adequate combination of classes, attributes and methods.

This paper presents some principles for the implementation a UML binary asso-

ciations in CSharp (C#), paying special attention to multiplicity and navigabil-

ity. Our implementation has some specification for bidirectional associations.

These principles have been used to write a series of code patterns that we use in

combination with using tools which generating code for associations, such as

Poseidon for UML and Enterprise Architect. These Tools are read from a UML

model stored in XMI (XML Metadata Interchange) format.

1 Introduction

One of the key building blocks in the Unified Modeling Language [UML] is the con-

cept of association. An "association" in UML is defined as a kind of relationship be-

tween classes (Actually classifiers. Classifier is a superclass of Class in the

UML metamodel

), which represents the semantic relationship between two or more

classes that involves connections (links) among their instances [1]. As it has been

denounced long ago [2], object-oriented programming languages express classifica-

tion and generalization well, but do not contain syntax or semantics to express asso-

ciations directly. Therefore, associations have to be implemented by an adequate

combination of classes, attributes and methods [3,9,11]. The simplest idea is to pro-

vide an attribute to store the links of the association, and accessor and mutator meth-

ods to manipulate the links. Other approaches emphasize the use of Java interfaces to

implement associations with some practical advantages [4, 13].

Poseidon UML[5] tools often provide some kind of code generation starting from

design models, but limited to skeletal code involving only generalizations and classes,

with attribute and method signatures, but no associations at all. The programmer has

to manually write the code to manage the associations in a controlled way, so that all

constraints and invariants are kept for correctness of the implementation. This is usu-

H. Khalifa I., A. Sarhan E. and S. A. Mahmoud M. (2005).

Generating Code for Mapping UML Associations Into C#.

In Proceedings of the Joint Workshop on Web Services and Model-Driven Enterprise Information Systems, pages 39-53

DOI: 10.5220/0002557200390053

 SciTePress

ally a repetitive task that could be automated to a certain extent. Besides, the number

of things that the programmer should bear in mind when writing the code for the asso-

ciations is so large, that he or she continuously risks forgetting some vital detail. This

is specially true when dealing with multiple (with multiplicity higher than 1) or bidi-

rectional (two-way navigable) associations. Moreover, the final written code is fre-

quently scattered over the code of the participating classes, making it more difficult to

maintain.

The aim of this work is three aims. First, write a series of code patterns that will

help programmers in mapping UML associations into a target object oriented pro-

gramming language. In this work, the language has been chosen to be CSharp (C#),

although the principles we have followed may be applied to other close languages like

C++, Java or the .NET framework. Second aim, using a tool that generates code for

associations using these patterns, the associations being read from a model stored in

XMI format. A third aim will be to enable reverse engineering, that is, obtaining the

associations between classes by analyzing the code that implements them. Although it

is a very simple and straightforward procedure if the code has been written with our

patterns.

Associations in UML can have a great variety of features. The present work is lim-

ited to the analysis and implementation of multiplicity and navigability in binary asso-

ciations. It excludes, therefore, more complex kinds of associations such as reflexive

associations, whole/part associations (aggregations and compositions), qualified asso-

ciations, association-classes, and n-ary associations [10]. It excludes, too, features

such as ordering, changeability, etc.

The following sections of this article are devoted to studying the features of multi-

plicity, navigability and visibility of associations, with a detailed analysis of the possi-

ble problems and proposed solutions. Then, Section 3 contains the description of a

uniform interface for all kinds of associations from the point of view of the participat-

ing classes, such as it is implemented by our patterns and source code. Finally, con-

clude briefly how to developed a concrete way of generating code of mapping UML

associations using C# code in this works.

2 The Problem of Multiplicity

The multiplicity of a binary association, placed on an association end (the target end),

specifies the number of target instances that may be associated with a single source

instance across the given association, in other words, how many objects of one class

(the target class) may be associated with a given single object from the other class (the

source class) [2]. The classical example in Figure 1 illustrates binary multiplicity.

Each instance of

Person may work for none or one instance of Company (0..1),

while each company may be linked to one or more persons (1..*). For those readers

less familiarized with UML notation, the symbol (*) stands for "many" (unbounded

number), and the ranges (1..1) and (0..*) may be abbreviated respectively as (1) and

(*).

Fig. 1. A classical example of binary association with the expression of multiplicities

Listing 1. Program code to maintain the binary association between Person and

Company

namespace model_1 {

public class Company

{

…………………………………

public Person[]person;

} }

namespace model_1 {

public class Person

{

…………………………

public Company company;

} }

The potential multiplicities in UML extend to any subset of nonnegative integers

[2], not only a single interval as (2..*), or a comma-separated list of integer intervals

as (1..3, 7..10, 15, 19..*): specifications of multiplicity like {prime numbers} or

{squares of positive integers} are also valid, although there is no standard notation for

them. Nevertheless, in UML as in other modeling techniques, the most usual multi-

plicities are (0..1), (1..1), (0..*) and (1..*). We are going to restrict our analysis to

multiplicities that can be expressed as a single integer interval in the form of

(min..max) notation. The multiplicity constraint is a kind of invariant, that is, a condi-

tion that must be satisfied by the system. A possible practice when programming is: do

not check always the invariant, but only at the request of the programmer, after com-

pleting a set of operations that are supposed to leave system in a valid state (a transac-

tion).

This practice is more efficient in run-time, and gives the programmer more free-

dom and responsibility in writing the code, with the corresponding risk that he or she

forgets putting the necessary checks and carelessly leaves the system in a wrong state.

On the other side, we think that checking multiplicity constraints is not very time con-

suming (inefficient), especially when compared with the time required to manage

collections or synchronize bidirectional associations (see Section 3). Therefore, we

think that it is worth doing as much as we can for the programmer, so that our first

target will be to analyze the possibility of performing automatic checks for multiplic-

ity constraints.

2.1 Optional and mandatory associations

The value of minimum multiplicity can be any positive integer, although the most

common values are 0 or 1. When the value is 0 we say the association is optional for

the class on the opposite end (class Person in Figure 1), when the value is 1 or

greater we say it is mandatory (class Company). Optional associations pose no spe-

cial problems for the implementation, but mandatory associations do. From a concep-

tual point of view, an object participating in a mandatory association needs to be

linked at any moment with one object (or more) on the other side of the association,

otherwise the system is in a wrong state. In the example given in Figure 1, an instance

of Company needs always an instance of Person. Therefore, in the same moment

you create the instance of Company, you have to link it to an instance of Person.

This can happen in three different ways:

• An instance of Company is created by an instance of Person and linked to

its creator.

• An instance of Company is created with an instance of Person supplied as

a parameter.

• An instance of Company is created and it issues the creation of an instance of

Person.

The third case poses additional problems. The creation of a Person will probably

require additional data, such as name, address, etc., and it does not seem very sensible

to supply them in the creation of a Company. This problem becomes much worse if

Person has other mandatory associations, for example one with the Country

where he or she lives: if this were the case, the creation of a Company would require

supplying data for creating a Person, for creating a Country, etc. The most obvi-

ous solution is to allow only the first and second forms of instantiation. But then sup-

pose the association is mandatory in both ends. Which instance is to be created first?

We have not a satisfactory choice, since we will put the system in a wrong state until

both creations are finished.

We could think of an atomic creation of both instances, but this is valid only for the

simplest case in which only two classes are involved. Should we define atomic crea-

tors for two, three, any number of classes? Similar problems arise when dealing with

object deletion. Imagine now that we are not creating or deleting instances, but chang-

ing links between instances.

If you want to change the instance of Company that is linked with a given instance

of Person, simply delete the link with the old Company and add a new link with

the new Company. This works as far as the old Company is linked to other in-

stances of Person; you can even delete the link and add no new one, since the asso-

ciation is optional for Person. If you had only one Person linked to a given Com-

pany, you should supply a new Person to the Company before deleting the link

with the old Person, but this is only the specified behavior (the association is man-

datory for Company) and you cannot complain about it. Nevertheless, we find new

problems here. If the association with Company were mandatory for Person too

(that is, 1..1 multiplicity instead of the current 0..1), the instance of Person could

not delete the old link with a Company and then add the new one, nor it could do it

in the reverse order, "first add then delete", because it would go through a wrong

system state. An atomic change of links would be valid only for the simplest cases,

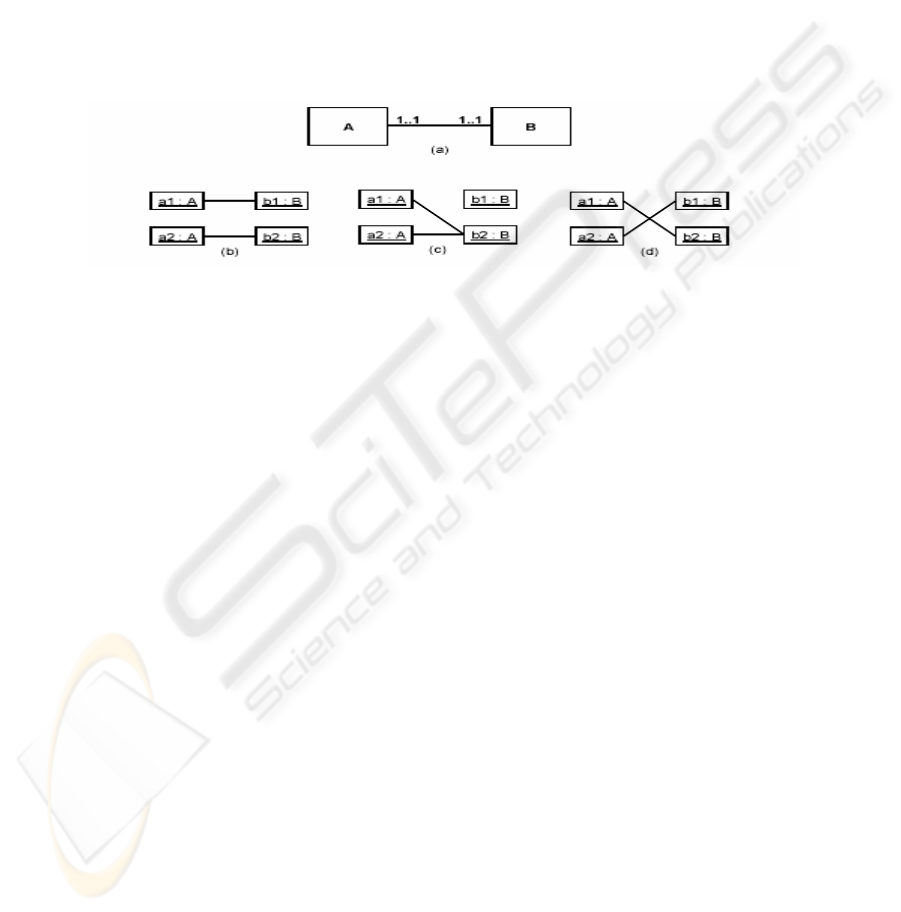
but not for more complex ones such as the following, rather twisted case (see Figure

2): consider classes A and B, which are associated with multiplicity 1..1 on both ends,

and the corresponding instances a1, a2, b1 and b2. In the initial state, we have the

links a1-b1 and a2-b2. In the final state, we want to have the links a1-b2 and

a2-b1. Even if we can change atomically a1-b1 to a1-b2 without violating the

multiplicity constraints on a1, this would leave b1 without any links and b2 with

two links until the final state is reached. We should have to perform the whole change

atomically by means of an atomic switch implemented in a single operation.

Fig 2. Multiplicity constraints can make very difficult changing links between instances with-

out entering a wrong system state: a) class diagram; b) initial state; c) intermediate wrong state;

d) final desired state.

Obviously, we cannot define a new operation to avoid any conceivable wrong state

involving several instances. In consequence, we think that mandatory associations

pose unsolvable problems regarding the creation and deletion of instances and links:

we cannot achieve with a few primitive operations that a mandatory association is

obeyed at any time, and we cannot isolate, inside atomic operations, the times when

the constraint is not obeyed. Therefore, we have to relax the implications of manda-

tory associations for the implementation, as other methods do [8]. This proposal is as

follows: do not check the minimum multiplicity constraint when modifying the links of

the association (mutator methods, or setters), but only when accessing them (accessor

methods, or getters). The programmer will be responsible for using the primitives in a

consistent way so that a valid system state is reached as soon as possible.

For example, you will be allowed to create a Company without linking it to any

Person, and you will be allowed to delete all the links of a Company with in-

stances of Person; but before accessing, for other purposes, the links of that particu-

lar instance of Company towards any instances of Person, you will have to restore

them to a valid state, otherwise you will get an invalid multiplicity exception, which

shall be defined in the code that implements the associations according to this pro-

posal [9,13].

2.2 Single and multiple associations

The value of maximum multiplicity in an association end can be any integer greater or

equal than 1, although the most common values are 1 or *. When the value is 1 we say

the association is single for the class on the opposite end (class Person in Figure 1),

when the value is 2 or greater we say it is multiple (class Company). Single associa-

tions are easier to implement than multiple associations: to store the only possible

instance of a single association we usually employ an attribute having the correspond-

ing target class as type, but to store the many potential links of a multiple association

we must use some kind of collection of objects, such as the C# predefined Length,

Hashtable, etc. In the general case we cannot use an array of objects, because it

gets a fixed size when it is instantiated. Since collections in C# can have any number

of elements, the maximum multiplicity constraint cannot be stated in the declaration of

the collection in the C# code, but it must be checked elsewhere during run-time.

We need two kinds of mutators, add and remove, which will accept as a parame-

ter either single objects or entire collections. Because of the problems with minimum

multiplicity explained above, the remover sometimes will leave the source instance in

a wrong state; we can't avoid this situation. The adder, instead, leaves us a wider

choice. If we try to add some links above the maximum multiplicity constraint, we can

choose between rejecting the addition or performing it; in the latter case we violate

temporarily the constraint until a call to the remover restores the source instance to a

safe state; the wrong state would only be detected by accessor methods, as we settled

in the case of minimum multiplicity. However, this is true only for multiple associa-

tions implemented with a collection; in single associations implemented by means of

an attribute we simply cannot violate the maximum multiplicity constraint: we are

forced to reject the addition.

If we choose to reject the addition, instead, besides having an asymmetric behavior

between remover and adder, we can find precedence problems when invoking the

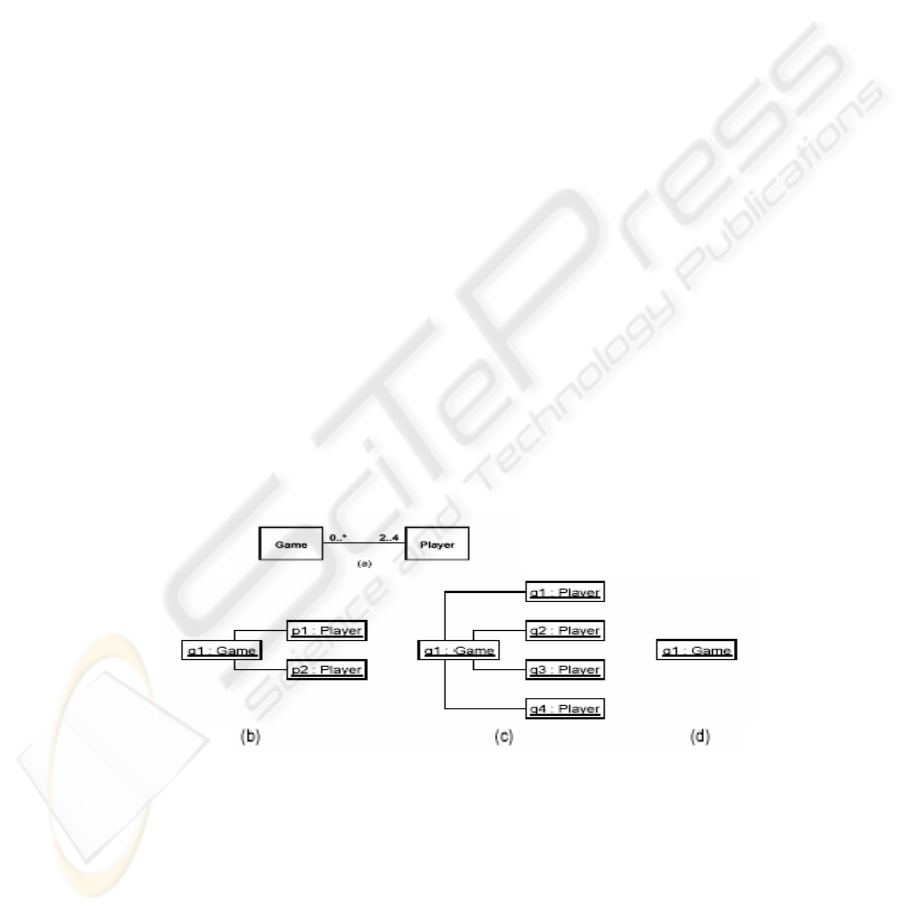
adder and the remover in succession. Consider class Game associated with class

Player with multiplicity 2..4 (see Figure 3), and suppose an instance g1 of Game

is linked to two instances p1, p2 of Player. We want to replace these two players

by four new different players q1, q2, q3, q4. If we issue "first remove then add", we

get finally what we want; if we issue "first add then remove", the addition is rejected

and the remotion leaves the instance of Game in a wrong state.

Fig 3. Precedence problems found when invoking the adder and the remover in succession: a)

class diagram of Game-Player association; b) initial state with players p1, p2; c) final

desired state after removing players p1, p2 and then adding players q1, q2, q3, q4; d) final

wrong state after unsuccessfully trying to add players q1, q2, q3, q4 and then removing

players p1, p2.

Listing 2. Program Code to maintain the binary association between Person and Com-

pany

namespace model_2 {

public class Game {

public Player m_Player;

public Game(){

}

~Game(){

}

public virtual void

Dispose(){

} }//end Game }//end

namespace model_2

namespace model_2 {

public class Player {

public Player(){

}

~Player(){

}

public virtual void

Dispose(){

}

}//end Player }//end

namespace model_2

In the end, we have preferred to reject the addition if it violates the maximum allowed, and

ask the users of mutator methods to use them always in the right order, first remove then add,

so that we can get an analogous behavior for single and multiple associations. Therefore, the

remover does not check the minimum multiplicity constraint (possibly leaving empty a manda-

tory association), the adder does check the maximum multiplicity constraint, and the getter

raises an exception if either constraint is not fulfilled. Accessor methods of multiple associa-

tions have another peculiarity, when compared with the accessors of single associations: they

return a collection of objects, not a single object, therefore the returned type is that of the col-

lection, not that of the target class. In our implementation, the returned type is the C# interface

Collection, which is implemented by all standard collections. Internally, we use a

Hashtable collection, which ensures that there are no duplicate links in an association, as

the UML requires [7].

Finally, the standard collections in C# are specified to contain instances of the standard class

Object, which is a superclass of every class in C#. You cannot specialize these collections to

store objects pertaining only to a particular class (That is, you cannot specialize them to modify

their storage structure, but you can modify their behavior so that they) store in effect only the

required objects, precisely by means of the run-time type checking method we describe.. This

means that, if we use a Hashtable inside Company to store the links to instances of Per-

son, we must ensure on our own that no one puts a link to an instance of another class such as

Dog or Report (this could happen if a collection of objects is passed as a parameter to the

add method). Therefore, the mutator methods must perform a run-time type checking by

means of explicit casting. If the type-check fails, then the link is not set to that object, and a

class cast exception, which is predefined in C#, is raised.

3 The Problem of Navigability

The directionality, or navigability, of a binary association, graphically expressed as an

open arrow at the end of the association line that connects two classes, specifies the

ability of an instance of the source class to access the instances of the target class by

means of the association instances (links) that connect them (An alternate definition:

the possibility for a source object to designate a target object through an association

instance (link), in order to manipulate or access it in an interaction with message inter-

changes. The Standard does not give a clear definition of navigability, as we have

shown in previous works where we have tried to clarify this topic [9,10,13]). In this

paper, we take navigability and directionality as synonyms. If the association can be

traversed in both directions, then it is bidirectional (two-way), otherwise it is unidirec-

tional (one-way).

A navigable association end, which is referenced by its rolename, defines a pseudo

attribute of the source class, so that the source instance can use the rolename in ex-

pressions in the same way as it uses its own attributes [6]. An instance can communi-

cate (by sending messages) with the connected instances of the opposite navigable end

[11], and it can use references to them as arguments or reply values in communica-

tions [7]. Similarly, if the association end is navigable, the source instance can query

and update the links that connect it to the target instances.

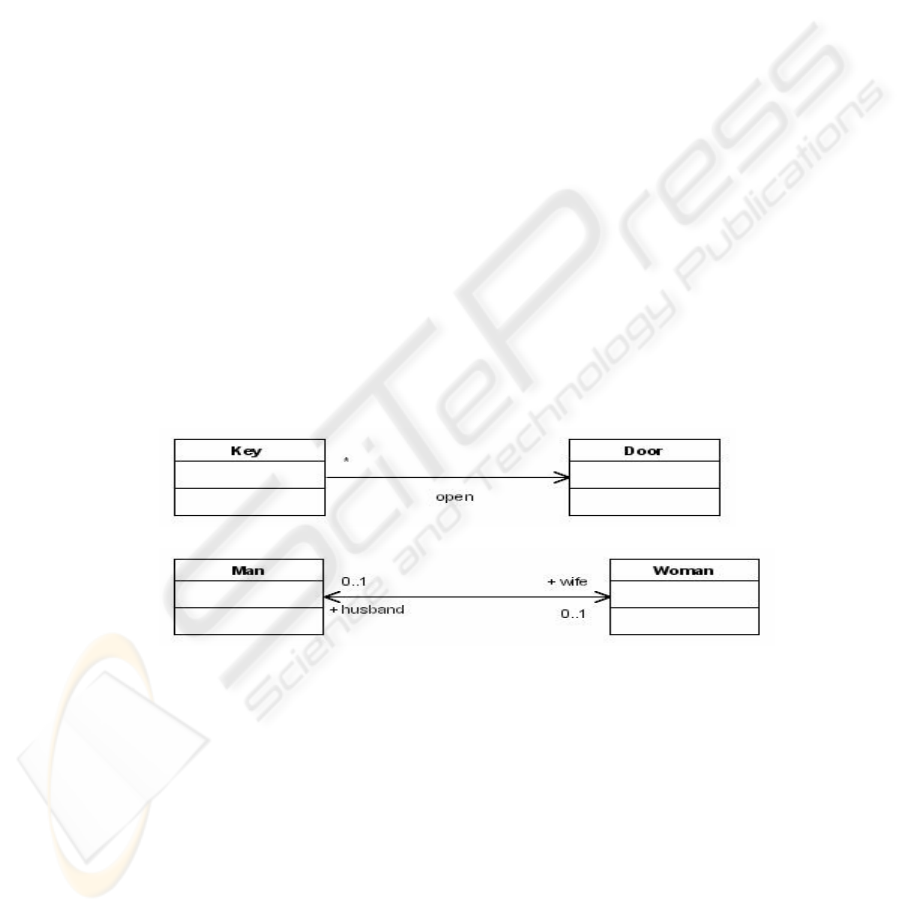
The examples in Figure 4 illustrate navigability. The association Key-Door is

unidirectional, meaning that a Key can access the Door it can open, but an instance

of Door does not know the set of instances of Key that can open it: the Door

cannot traverse the connections (links) against the navigability of the association. On

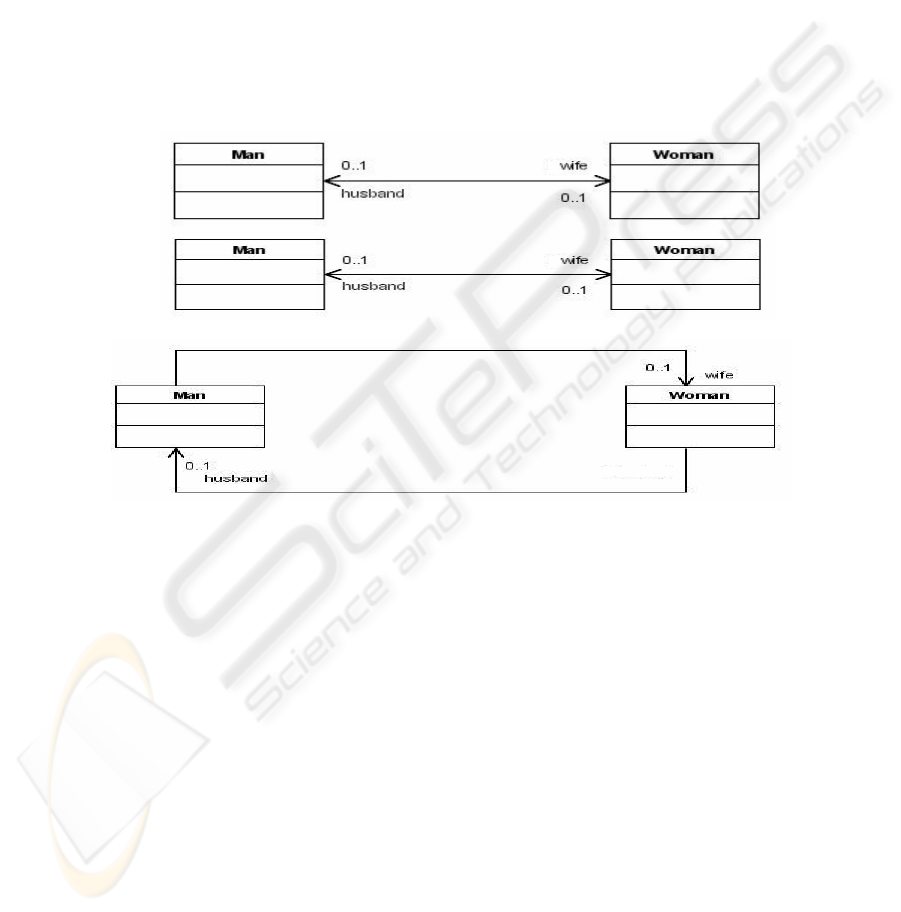
the other side, the association Man-Woman is bidirectional, meaning that connected

instances of these classes know each other.

a) Unidirectional

b) Bidirectional

Fig 4. Examples of a) Unidirectional and b) Bidirectional Associations.

The arrowheads can be shown or omitted in a bidirectional association [14]. Unfor-

tunately, this leads to an ambiguity in the graphical notation, because we cannot

. dis-

tinguish between bidirectional associations and associations with unspecified naviga-

bility. Or, worse, unspecified associations are assumed to be bidirectional without

further analysis [10].

Listing 3. Program code to maintain the unidirectional and bidirectional associations

namespace model_3 {

public class Key_ {

………………………………

public Door door;

} }

public class Door {

…………………

}

namespace model_4 {

public class Woman {

…………………………………….

public Man husband;

} }

public class Man {

……………………………

public Woman woman; }

3.1 Unidirectional associations

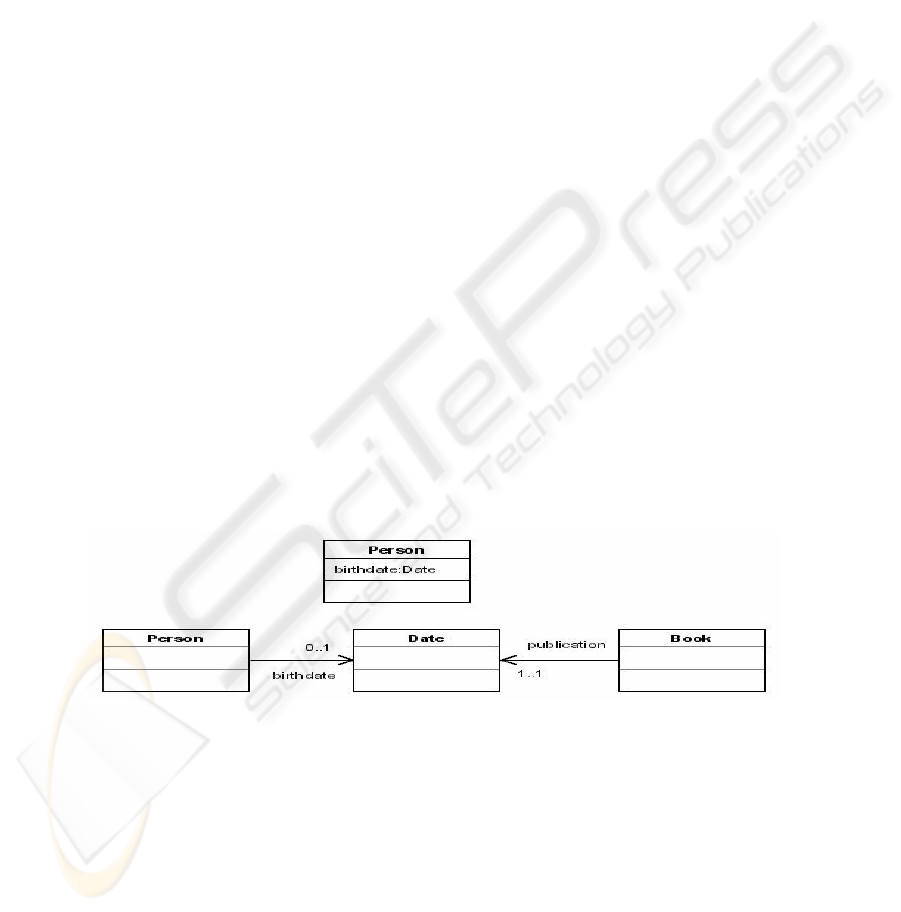
A single unidirectional association is very similar to a single valued attribute in the

source class, of the type of the target class: an embedded reference, pointer, or what-

ever you want to call it. The equivalence, however, is not complete. Whereas the at-

tribute value is "owned" by the class instance and has no identity, an external refer-

enced object has identity and can be shared by instances of other classes that have a

reference to the same object [12] (see Figure 5). Anyhow, the equivalence is satisfac-

tory enough to serve as a basis for the implementation of this kind of associations. In

fact, in C# there is no difference at all: except for the case of primitive values, attrib-

utes in C# are objects with identity, and if they are public you cannot avoid them to be

referenced and shared by other objects.

Fig. 5. Partial equivalence between a) attribute and b) single unidirectional association.

Listing 4. Program code to maintain the Partial equivalence between attribute and

single unidirectional association

namespace model_2 {

public class Person {

…………………………..

public Date birthdate;

}

public class Date {

/// Attributes – Asso-

ciation End

public class Book {

…………………………………

public Date publica-

tion;

}

A multiple unidirectional association is a bit more complicated, although the im-

plementation can be based on the same principles, since it can be assimilated to a

multivalued attribute (UML allows multiplicity in attributes, thus multivalued attrib-

utes [8]). To manage the collection of objects on the navigable end, however, we need

an additional object of a standard collection class, which is a Hashtable in our

implementation (see Figure 6).

(a)

(b)

Fig. 6. Multiple unidirectional association: a) analysis diagram and b) design diagram.

A new object must be inserted to manage the collection of target objects. The stan-

dard collections in C#, such as Hashtable, are defined for the standard class Ob-

ject, which is a superclass of every class; therefore, mutator methods must ensure

that the objects contained in the collection parameter are of the appropriate type be-

fore adding them to the collection attribute. Therefore, the type of the attribute used to

implement the association inside the source class is not any more the target class itself,

but the Hashtable class or another convenient collection class. The methods to

manage the association will have to accomplish some additional tasks. Mutators can

add or remove not only single objects of the class target, but also entire collections;

thus, the type of the parameter will be either the target class of the association or the

intermediate collection class.

In this case, mutator methods must ensure that the objects contained in the collec-

tion parameter are of the appropriate type before adding them to the collection attrib-

ute. Accessors, as we have already explained (see Section 2), do not return a single

object, but a collection of objects, even when the collection is made up of only one

element. The returned collection object is not identically the same one that is stored

inside the source class, but a clone (a new object with a collection of references to the

same target elements), because the original collection object must remain completely

encapsulated inside the source object (represented by the composition in Figure 6).

Listing 6. Program code to maintain the Multiple unidirectional association analysis

and design diagrams

namespace model_6 {

public class Recipe

{

…………………………………

public Aliment[]

ingredient;

………………………………….

public Aliment ali-

ment;

} }

public class Aliment {

…………………………

public Recipe recipe;

}

public class Recipe {

……………………….

public HashTable

hashTable;

public HashTable

hashTable_1; }

public class Aliment :

Object {

}

public class HashTable

{

………………………………

public Recipe recipe;

……………………………

public Object[] object;

}

public class Object {

……………………………..

public HashTable

hashTable_2;

}

As the diagrams in Figures 5 and 6 show, in our opinion the multiplicity constraint

in a design model can be specified only for a navigable association end. Indeed, the

multiplicity is a constraint that must be evaluated within the context of the class that

owns the association end; if that class knows the constraint, then it knows the associa-

tion end, that is, the end is navigable. You cannot restrict the number of objects con-

nected to a given instance unless this instance has some knowledge of the connected

objects, that is, unless you make the association end navigable. Therefore, the need for

a multiplicity constraint other than 0..* (that is, unrestricted) is an indication that the

association end must be navigable. In consequence, unidirectional associations with

multiplicity constraints on the nonnavigable association end must be rejected in code

generation.

3.2 Bidirectional associations

The partial equivalence between attributes and unidirectional associations is not any

more found among bidirectional associations. Instead, an instance of a bidirectional

association is more like a tuple of elements [14]. Combining the multiplicities in both

association ends, we can have three cases: single-single, single-multiple, and multi-

ple_multiple.

a) analysis diagram

b) design diagram.

Fig. 7. Single-single bidirectional association: a) analysis diagram and b) design diagram

Listing 7. Program code to maintain the Single-single bidirectional association analy-

sis and design diagrams

namespace model_7 {

public class Man {

……………………

public Woman woman; } }

public class Woman {

/// Attributes – AssociationEnd and AssociationEnd hus-

band

public Man husband; } }

The implementation of the association's mutators must ensure that the husband of

the wife of a given man is that man himself, and vice versa.An easy way to implement

a single-single bidirectional association is by means of two synchronized single unidi-

rectional associations (see Figure 7). The synchronization of the two halves must be

preserved by the mutator methods on each side: every time an update is requested on

one side, the other side must be informed to perform the corresponding update; the

update is accomplished only if both sides agree that they can perform it while keeping

maximum multiplicity constraints.

A single-multiple bidirectional association can be implemented in a similar way,

combining a single unidirectional association and a multiple unidirectional associa-

tion. And, finally, a multiple-multiple bidirectional association is achieved by means

of two multiple unidirectional associations (see Figure 8).

Synchronization becomes progressively a more and more complex issue when one

or both association ends are multiple. Consider the example given in Figure 8. Sup-

pose you want to add an author to a particular Book instance; you do this by issuing

the add method on the Book instance, and passing a Person instance as a pa-

rameter. If the Book can have more authors without violating its maximum multiplic-

ity (which is 3), then it requests the author to add the Book itself to the collection of

publications the Person has; this can fail if the maximum multiplicity constraint for

the number of publications (in this case, 10) is violated. If the request to the author

succeeds, then the Book updates its side.

Now, you can try adding a collection of authors to a Book, too. As one can expect,

the Book requests each one of the authors to add the Book itself as a publication; if

only one of the authors fails to add the Book, then the whole operation must be un-

done, since an update must be atomic: all or none.

Fig. 8. Multiple-multiple bidirectional association: analysis and design diagrams

Similar considerations apply to the remove mutator, bearing in mind that the

remove method is performed even if the minimum multiplicity constraint is not

kept, therefore it can leave the source instance or any of the affected target instances

in an invalid state.

4 Conclusions

In this work we have developed a concrete way of generating code of mapping UML

associations using C# code: we have written specific code patterns, and we have using

a tool that reads a UML design model stored in XMI format and generates the neces-

sary C# files. We have paid special attention to two main features of associations:

multiplicity and navigability. This analysis has encountered difficulties that may re-

veal some weaknesses of the UML Specification.

However, different tool options will allow the user to override the automatic multi-

plicity and type checks when generating code, in favor of efficiency. Besides, we have

argued that unidirectional associations should not have a multiplicity constraint on the

source end in a design model, and bidirectional associations should not have both ends

with private (or protected) visibility; therefore, the tool will reject the generation of

code for these associations. Again, the user will be able to disable this model-

correctness checking and issue the code generation at his/her own risk.

This work can be continued on several lines. First, implementation of other associa-

tion end properties, such as ordering, changeability, interface specified, xored associa-

tions, and so on. Second, specific implementation of particular kinds of binary asso-

ciations, such as reflexive associations, aggregations and compositions. Third, im-

plementation of more complex associations: qualified associations, associations

classes, and n-ary associations. Fourth, expand the tool to perform reverse engineer-

ing, that is, obtaining the associations between classes by analyzing the code that im-

plements them.

References

1. Object Management Group. XML Metadata Interchange (XMI) Specification, Version 1.2,

January 2002. Available at http://www.omg.org/.

2. James Rumbaugh. "A Search for Values: Attributes and Associations". Journal of Object

Oriented Programming, 9(3):6-8, June 1996.

3. Scott W. Ambler. “An Overview of Object Relationships”, “Unidirectional Object Rela-

tionships”, “Implementing One-to-Many Object Relationships”, “Implementing Many-to-

Many Object Relationships”. A series of tips to be found at IBM Developer Works,

http://www-106.ibm.com/developerworks/.

4. Hermann Kaindl. “Difficulties in the Transition from OO Analysis to Design”. IEEE Soft-

ware, 16(5):94-102 (1999).

5. The Poseidon UML tool, http://www.gentleware.com//

6. James Rumbaugh. "Relations as Semantic Constructs in an Object- Oriented Language", In

Proceedings of the ACM Conference on Object-Oriented Programming: Systems, Lan-

guages and Applications, pp. 466-481, Orlando, Florida, 1987.

7. Object Management Group. Unified Modeling Language (UML) Specification, Version 1.4,

September 2001 (Version 1.3, June 1999). Available at http://www.omg.org/.

8. Perdita Stevens. “On the Interpretation of Binary Associations in the Unified Modelling

Language”, Journal on Software and Systems Modeling, 1(1):68-79 (2002). A preliminar

version in: Perdita Stevens. "On Associations in the Unified Modeling Language". The

Fourth International Conference on the Unified Modeling Language, UML'2001, October

1-5, 2001, Toronto, Ontario, Canada. Published in Lecture Notesin Computer Science 285,

Springer 2001, pp. 361-375.

9. Gonzalo Génova. "Semantics of Navigability in UML Associations". Technical Report

UC3M-TR-CS-2001-06, Computer Science Department, Carlos III University of Madrid,

November 2001, pp. 233-251.

10. Gonzalo Génova, Juan Llorens, Paloma Martínez. “The Meaning of Multiplicity of N-ary

Associations in UML”, Software and Systems Modeling, 1(2): 86-97, 2002. A preliminary

version in: Gonzalo Génova, Juan Llorens, Paloma Martínez. “Semantics of the Minimum

Multiplicity in Ternary Associations in UML”. The 4th International Conference on the

Unified Modeling Language-UML'2001, October 1-5 2001, Toronto, Ontario, Canada.

Published in Lecture Notes in Computer Science 285, Springer 2001, pp. 329-341.

11. Gonzalo Génova, Juan Llorens, Vicente Palacios. "Sending Messages in UML", Journal of

Object Technology, vol.2, no.1, Jan-Feb 2003, pp. 99- 115,

http://www.jot.fm/issues/issue_2003_01/article3.

12. Il-Yeol Song, Mary Evans, E.K. Park. "A Comparative Analysis of Entity- Relationship

Diagrams", Journal of Computer and Software Engineering, 3(4):427-459 (1995).

13. William Harrison, Charles Barton, Mukund Raghavachari. "Mapping UML Designs to

Java". The 15th Annual ACM Conference on Object-Oriented Programming, Systems, Lan-

guages, and Applications-OOPSLA’2000, October 15-19 2000, Minneapolis, Minnesota,

United States. ACM SIGPLAN Notices, 35(10): 178-187. ACM Press, New York, NY,

USA.

14. Guy Genilloud. "Informal UML 1.3 - Remarks, Questions, and some Answers". UML

Semantics FAQ Workshop (held at ECOOP'99), Lisbon, Portugal, June 12th 1999.

15. The Fujaba CASE Tool, University of Paderborn, http://www.fujaba.de/.

16. Java Community Process. Java Metadata Interface (JMI) Specification, Version 1.0, June

2002. Available at http://www.jcp.org/.