An Approach to Natural Language Understanding

Based on a Mental Image Model

Masao Yokota

Department of System Management, Faculty of Information Engineering,

Fukuoka Institute of Technology, 3-30-1 Wajirohigashi, Higashi-ku,

Fukuoka-shi, 811-0295 Japan

Abstract.

The Mental Image Directed Semantic Theory (MIDST) has proposed

an omnisensual mental image model and its description language L

. This pa-

per presents a brief sketch of the MIDST, and focuses on word meaning de-

scription and text understanding in association with the mental image model in

view of cross-media reference between text and picture.

1 Introduction

The need for more human-friendly intelligent systems has been brought by rapid

increase of aged societies, floods of multimedia information over the WWW, devel-

opment of robots for practical use and so on.

For example, it is very difficult for people to

exploit necessary information from

the immense multimedia contents over the WWW. It is still more difficult to search

for desirable contents by queries in different media, for example, text queries for

pictorial contents. In this case, intelligent systems facilitating cross-media reference

are very helpful.

In order to realize these kinds of intelligent systems, we think it is very important

to develop such a com

putable knowledge representation language for multimedia

contents that should have at least a capability of representing spatio-temporal events

that people perceive in the real world. In this research area, it is most conventional

that conceptual contents conveyed by information media such as language and picture

are represented in computable forms independent of each other and translated via

‘transfer’ processes which are often specific to task domains [10], [11].

Yokota, M. et al have proposed a semantic t

heory of natural language based on an

omnisensual image model, so called, ‘Mental Image Directed Semantic Theory

(MIDST)’ [1]. In the MIDST, the concepts conveyed by such syntactic components

as words, phrases, clauses and so on are associated with mental imagery of the exter-

nal or physical world and formalized in an intermediate language L

[3].

is employed for

many-sorted predicate logic with five types of terms. The most

remarkable feature of L

is its capability of formalizing both temporal and spatial

Yokota M. (2005).

An Approach to Natural Language Understanding Based on a Mental Image Model.

In Proceedings of the 2nd International Workshop on Natural Language Understanding and Cognitive Science, pages 22-31

DOI: 10.5220/0002562400220031

 SciTePress

event concepts on the level of human sensations while the other similar knowledge

representation languages are designed to describe the logical relations among concep-

tual primitives represented by lexical tokens [5], [6], [7].

The language L

has already been implemented on several versions of the intelli-

gent system IMAGES [1], [2], [3], [4] and there is a feedback loop between them for

their mutual refinement, unlike the other similar ones [8], [9].

This paper presents a brief sketch of the MIDST, and focuses on word meaning de-

scription and text understanding in association with the mental image model in view

of cross-media reference between text and picture.

2 A Brief Sketch of MIDST

The MIDST is still under development and intended to provide a formal system,

represented in L

, for natural semantics of space and time. This system is one kind

of applied predicate logic consisting of axioms and postulates subject to human per-

ceptive processes of space and time, while the other similar systems in Artificial In-

telligence [12], [13], [14] are objective, namely, independent of human perception

and do not necessarily keep tight correspondences with natural language.

2.1 Omnisensual image model

The MIDST treats word meanings in association with mental images, not limited to

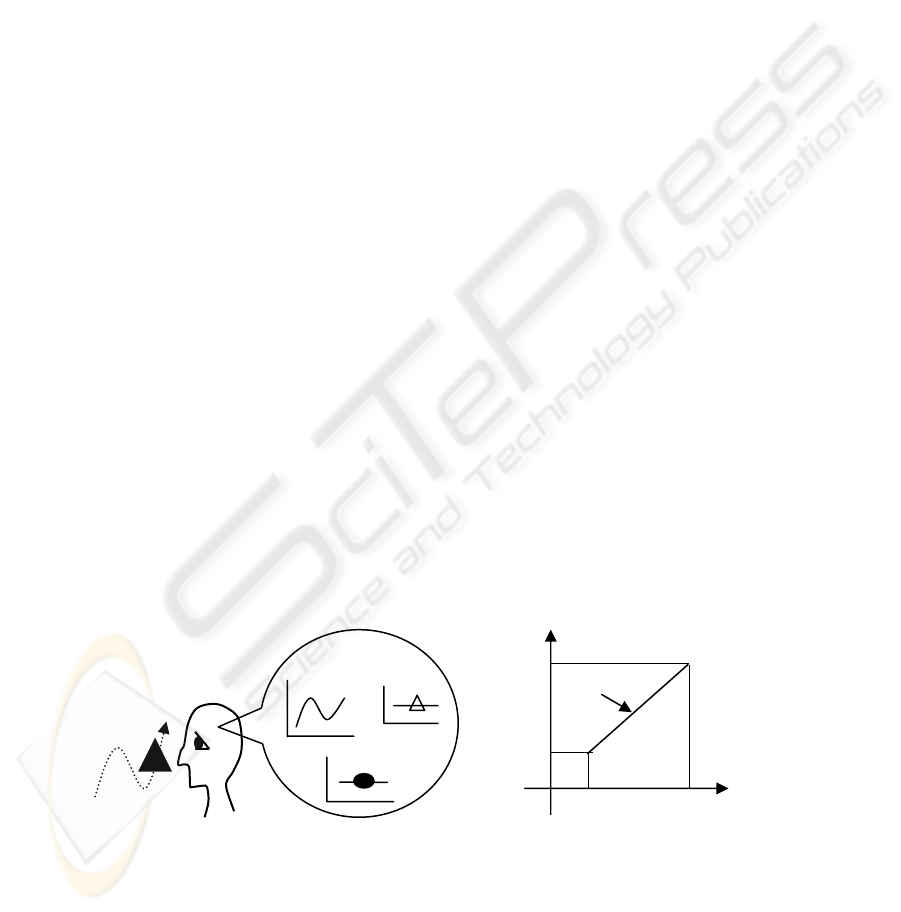
visual but omnisensual, modeled as “Loci in Attribute Spaces” [1], [2], [3], [4]. An

attribute space corresponds with a certain measuring instrument just like a barometer,

a map measurer or so and the loci represent the movements of its indicator.

For example, the moving black triangular object shown in Fig.1-a is assumed to be

perceived as the loci in the three attribute spaces, namely, those of ‘Location’, ‘Color’

and ‘Shape’ in the observer’s brain.

A general locus is to be articulated by “Atomic Locus” with the duration [t

, t

] as

depicted in Fig.1-b and formalized as (1).

L(x,y,p,q,a,g,k) (1)

Attribute

(

)

Location Shape

Colo

(a) (b)

Fig.1. Mental image model: (a) Attribute spaces and (b) Atomic locus.

This is a formula in many-sorted first-order predicate logic, where “L” is a predi-

cate constant with five types of terms: “Matter” (at ‘x’ and ‘y’), “Attribute Value” (at

‘p’ and ‘q’), “Attribute” (at ‘a’), “Event Type” (at ‘g’) and “Standard” (at ‘k’). Con-

ventionally, Matter variables are headed by ‘x’, ‘y’ and ‘z’ and often placed at Attrib-

ute Values or Standard to represent their values at the time. The formula is called

‘Atomic Locus Formula’ whose first two arguments are sometimes referred to as

‘Event Causer (EC)’ and ‘Attribute Carrier (AC)’, respectively.

The intuitive interpretation of (1) is given as follows, where ‘matter’ refers ap-

proximately to ‘object’ or ‘event’.

“Matter ‘x’ causes Attribute ‘a’ of Matter ‘y’ to keep (p=q) or change (p ≠ q) its

values temporally (g=Gt) or spatially (g=Gs) over a time-interval, where the values

‘p’ and ‘q’ are relative to the standard ‘k’.”

When g=Gt and g=Gs, the locus indicates monotonic change or constancy of the

attribute in time domain and that in space domain, respectively. The former is called

‘temporal event’ and the latter, ‘spatial event’.

For example, the motion of the ‘bus’ represented by S1 is a temporal event and the

ranging or extension of the ‘road’ by S2 is a spatial event whose meanings or con-

cepts are formalized as (2) and (3), respectively, where the attribute is ‘Physical Lo-

cation’ denoted by ‘A12’.

(S1) The bus runs from Tokyo to Osaka.

(

∃

x,y,k)L(x,y,Tokyo,Osaka,A12,Gt,k)

∧

bus(y) (2)

(S2) The road runs from Tokyo to Osaka.

(

∃

x,y,k)L(x,y,Tokyo,Osaka,A12,Gs,k)

∧

road(y) (3)

2.2 Tempo-logical connectives

The duration of an atomic locus, suppressed in the atomic locus formula, corresponds

to the time-interval over which the Focus of the Attention of the Observer (FAO) is

put on the corresponding phenomenon outside.

The MIDST has employed ‘tempo-logical’ connectives representing both logical

and temporal relations between loci. A tempo-logical connective

is defined by (4),

where

and

refer to one of the temporal relations indexed by ‘i’, a locus, and an

ordinary binary logical connective such as the conjunctive ‘∧’, respectively. This is

more natural and economical than explicit indication of time intervals, considering

that people do not consult chronometers all the time in their daily lives.

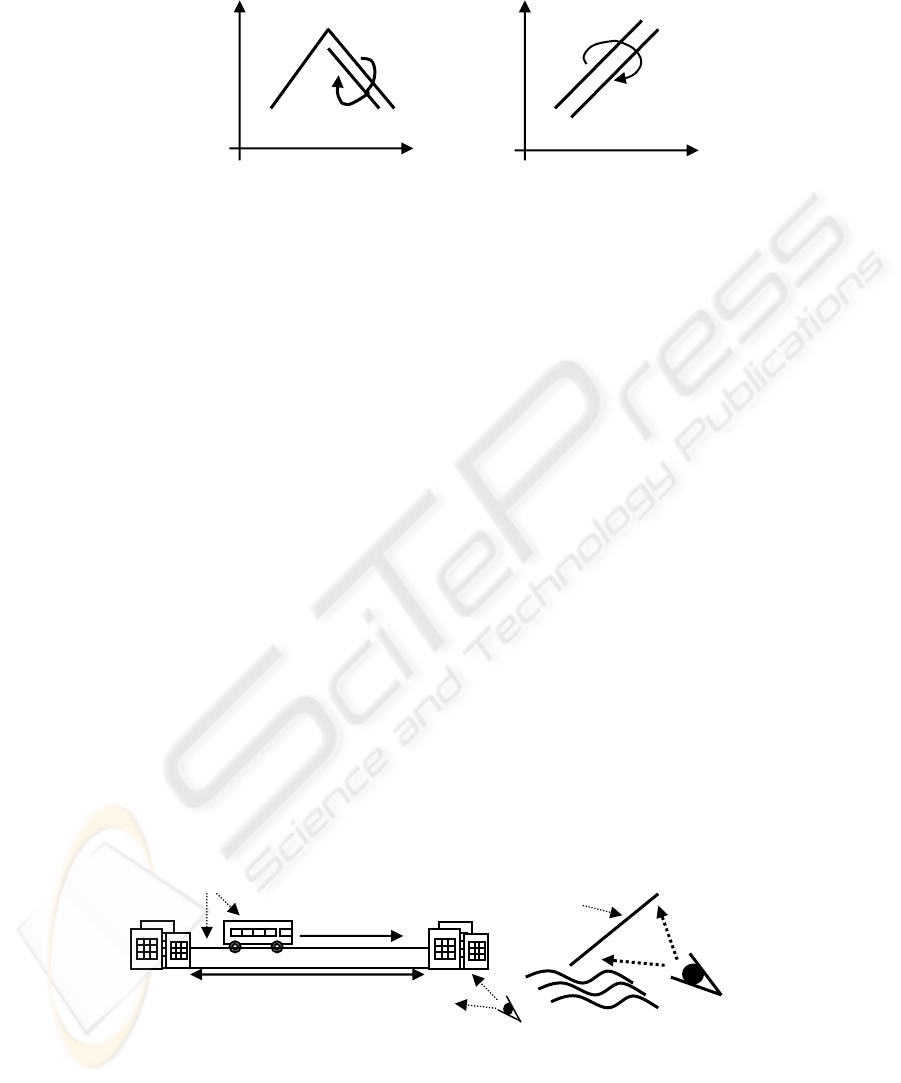
The expression (5) is the conceptual description of the English verb ‘fetch’ de-

picted as Fig.2-a, implying such a temporal event that ‘x’ goes for ‘y’ and then comes

back with it, where ‘Π’and ‘•’ are instances of the tempo-logical connectives,

‘SAND’ and ‘CAND’, standing for ‘Simultaneous AND’ and ‘Consecutive AND’,

respectively. In general, a series of atomic locus formulas with such connectives is

simply called ‘Locus formula’.

⇔

(

)

∧

(

) (4)

(

∃

x,y,p1,p2,k) L(x,x,p1,p2,A12,Gt,k)

•

((L(x,x,p2,p1,A12,Gt,k)

L(x,y,p2,p1,A12,Gt,k))

∧

≠

∧

≠

p2 (5)

time

t1 t2 t3

A12

time

A12

(a) (b)

Fig.2. Conceptual images: (a) ‘fetch’ and (b) ‘carry’.

Additionally, Fig.2-b shows the conceptual image of the English verb ‘carry’ that

is also included in the conceptual image of ‘fetch’. These are called ‘Event Patterns’

and about 40 kinds of event patterns have been found concerning the attribute ‘Physi-

cal Location (A12)’, for example, start, stop, meet, separate, return, etc [1].

Furthermore, a very important concept called ‘Empty Event (EE)’ and symbolized

as ‘ε’ is introduced. An EE stands for nothing but for time collapsing and is explicitly

defined as (6) with the attribute ‘Time Point (A34)’. It is essentially significant for the

MIDST that every temporal relation can be represented by a combination of Empty

Events, SANDs and CANDs. For example, (7) represents ‘X

during X

’.

According to this scheme, the duration [p, q] of an arbitrary locus X can be ex-

pressed as (8).

⇔

(

∃

x,y,p,q,g,k) L(x,y,p,q,A34,g,k) (6)

(

•

•ε

)

(7)

(p,q) (8)

2.3 Event types

It has been often argued that human active sensing processes may affect perception

and in turn conceptualization and recognition of the physical world. The difference

between temporal and spatial event concepts can be attributed to the relationship

between the Attribute Carrier (AC) and the Focus of the Attention of the Observer

(FAO). To be brief, the FAO is fixed on the whole AC in a temporal event but runs

about on the AC in a spatial event.

(a) (b)

AC FAO

Tokyo Temporal event Osaka

Spatial event FAO

Fig.3. FAO movement: (a) event types and (b) ‘slope’ as a spatial event.

Consequently, as shown in Fig.3-a, the bus and the FAO move together in the case

of S1 while the FAO solely moves along the road in the case of S2. That is, all loci in

Attribute spaces correspond one to one with movements or, more generally, tempo-

ral events of the FAO.

Therefore, S3 and S4 refer to the same scene in spite of their appearances as shown

in Fig.3-b where, as easily imagined, what ‘sinks’ or ‘rises’ is the FAO, and whose

conceptual descriptions are given as (9) and (10), respectively.

Such a fact is generalized as ‘ Postulate of Reversibility of a Spatial event (PRS) ’

that can be one of the principal inference rules belonging to people’s common-sense

knowledge about geography. This postulation is also valid for such a pair of S5 and

S6 interpreted as (11) and (12), respectively, where ‘A13’, ‘↑’ and ‘↓’ refer to the

attribute ‘Direction’ and its values ‘upward’ and ‘downward’, respectively. These

pairs of conceptual descriptions are called equivalent in the PRS, and the paired

sentences are treated as paraphrases each other.

(S3) The path sinks to the brook.

(

∃

x,y,p,z,k1,k2)L(x,y,p,z,A12,Gs,k1)

L(x,y,↓,↓,A13,Gs,k2)

∧

path(y)

∧

brook(z)

∧

≠

z (9)

(S4) The path rises from the brook.

(

∃

x,y,p,z,k1,k2)L(x,y,z,p,A12,Gs,k1)

L(x,y,↑,↑,A13,Gs,k2)

∧

path(y)

∧

brook(z)

∧

≠

z (10)

(S5) Route A and Route B meet at the city.

(

∃

x,p,y,q,k)L(x,Route_A,p,y,A12,Gs,k)

L(x,Route_B,q,y,A12,Gs,k)

∧

city(y)

∧

≠

q (11)

(S6) Route A and Route B separate at the city.

(

∃

x,p,y,q,k)L(x,Route_A,y,p,A12,Gs,k)

L(x,Route_B,y,q,A12,Gs,k)

∧

city(y)

∧

≠

q (12)

2.4 Attributes and standards

The attribute spaces for humans correspond to the sensory receptive fields in their

brains. At present, about 50 attributes concerning the physical world have been ex-

tracted exclusively from English and Japanese words as shown in Table 1. They are

associated with all of the 5 senses (i.e. sight, hearing, smell, taste and feeling) in our

everyday life while those for information media other than languages correspond to

limited senses. For example, those for pictorial media, marked with ‘*’ in Table 1,

associate limitedly with the sense ‘sight’ as a matter of course. The attributes of this

sense occupy the greater part of all, which implies that the sight is essential for hu-

mans to conceptualize the external world by. And this kind of classification of attrib-

utes plays a very important role in our cross-media referencing system [3].

Correspondingly, six categories of standards shown in Table 2 have been extracted

that are assumed necessary for representing values of each attribute in Table 1. In

general, the attribute values represented by words are relative to certain standards as

explained briefly in Table 2.

Table 1. A part of attributes extracted from linguistic expressions.

The properties “S” and “V” represent “scalar” and “vector”, respectively.

Code Attribute [Property] Linguistic expressions for attribute values.

*A01

PLACE OF EXISTE NCE [V] He is in Tokyo. The accident happened in Osaka.

*A02

LENGTH [S] The stick is 2 meters long (in length).

………………………………………

*A12

PHYSICAL LOCATION [V] Tom moved to Tokyo.

*A13

DIRECTION [V] The box is to the left of the chair.

*A14

ORIENTATION [V] The door faces to south.

*A15

TRAJECTORY [V] The plane circled in the sky.

*A16

VELOCITY [S] The boy runs very fast.

*A17

DISTANCE [S] The car ran ten miles.

A18

STRENGTH OF EFFECT [S] He is very strong.

………………………………………

*A32

COLOR [V] The apple is red. Tom painted the desk white.

A33

INTERNAL SENSATION [V] I am very tired.

A34

TIME POINT [S] It is ten o’clock.

………………………………………

Table 2. Standards of attribute values.

Categories of

standards

Remarks

Rigid Standard Objective standards such as denoted by measuring units (meter, gram, etc.).

Species Standard The attribute value ordinary for a species. A short train is ordinarily longer than a l

ong pencil.

Proportional Stand

ard

‘Oblong’ means that the width is greater than the height at a physical object.

Individual Standard Much money for one person can be too little for another.

Purposive Standard One room large enough for a person’s sleeping must be too small for his jogging.

Declarative Standar

The origin of an order such as ‘next’ must be declared explicitly just as ‘next to him

’

3 Word meaning description

A word meaning description M

is given by (13) as a pair of ‘Concept Part (C

)’ and

‘Unification Part (U

)’.

⇔ [C

] (13)

The C

of a word W is a logical formula while its U

is a set of operations for uni-

fying the C

s of W’s syntactic governors or dependents. For example, the meaning of

the English verb ‘carry’ is approximately given by (14).

[(

∃

x,y,p1,p2,k) L(x,x,p1,p2,A12,Gt,k)

L(x,y,p1,p2,A12,Gt,k)

∧

≠

∧

≠

p2:

ARG(Dep.1,x); ARG(Dep.2,y);] (14)

The U

above consists of two operations to unify the arguments of the first de-

pendent (Dep.1) and the second dependent (Dep.2) of the current word with the vari-

ables x and y, respectively. Here, Dep.1 and Dep.2 refer to the ‘subject’ and the ‘ob-

ject’ of ‘carry’, respectively. Therefore, the sentence ‘Mary carries a book’ is trans-

lated into (15).

(

∃

y,p1,p2,k) L(Mary,Mary,p1,p2,A12,Gt,k)

L(Mary,y,p1,p2,A12,Gt,k)

∧

Mary

≠

∧

≠

∧

book(y) (15)

For another example, the meaning description of the English preposition ‘through’

is also approximately given by (16).

[(

∃

x,y,p1,z,p3,g,k,p4,k0) (L(x,y,p1,z,A12,g,k)

•

L(x,y,z,p3,A12,g,k))

L(x,y,p4,p4,A13,g,k0)

∧

≠

∧

≠

p3: ARG(Dep.1,z);

IF(Gov=Verb)

→

PAT(Gov,(1,1)); IF(Gov=Noun)

→

ARG(Gov,y);] (16)

The U

above is for unifying the C

s of the very word, its governor (Gov, a verb or

a noun) and its dependent (Dep.1, a noun). The second argument (1,1) of the com-

mand PAT indicates the underlined part of (16) and in general (i,j) refers to the partial

formula covering from the ith to the jth atomic formula of the current C

. This part is

the pattern common to both the C

s to be unified. This is called ‘Unification Handle

)’ and when missing, the C

s are to be combined simply with ‘∧’.

Therefore the sentences S7, S8 and S9 are interpreted as (17), (18) and (19), re-

spectively. The underlined parts of these formulas are the results of PAT operations.

The expression (20) is the C

of the adjective ‘long’ implying ‘there is some value

greater than some standard of length (A02)’ which is often simplified as (20’).

(S7) The train runs through the tunnel.

(

∃

x,y,p1,z,p3,k,p4,k0) (L(x,y,p1,z,A12,Gt,k)

•

L(x,y,z,p3,A12,Gt,k))

L(x,y,p4,p4,A13,Gt,k0)

∧

≠

∧

≠

∧

train(y)

∧

tunnel(z) (17)

(S8) The path runs through the forest.

(

∃

x,y,p1,z,p3,k,p4,k0) (L(x,y,p1,z,A12,Gs,k)

•

L(x,y,z,p3,A12,Gs,k))

L(x,y,p4,p4,A13,Gs,k0)

∧

≠

∧

≠

∧

path(y)

∧

forest(z) (18)

(S9) The path through the forest is long.

(

∃

x,y,p1,z,p3,x1,k,q,k1,p4,k0) (L(x,y,p1,z,A12,Gs,k)

•

L(x,y,z,p3,A12,Gs,k))

L(x,y,p4,p4,A13,Gs,k0)

∧

L(x1,y,q,q,A02,Gt,k1)

∧

≠

∧

≠

∧

q>k1

∧

path(y)

∧

forest(z) (19)

(

∃

x1,y1,q,k1)L(x1,y1,q,q,A02,Gt,k1)

∧

q>k1 (20)

(

∃

x1,y1,k1)L(x1,y1,Long,Long,A02,Gt,k1) (20’)

4 Text Understanding and Cross-Media Reference

Every version of the intelligent system IMAGES can perform text understanding

based on word meaning descriptions as follows.

Firstly, a text is parsed into a surface dependency structure (or more than one if

syntactically ambiguous). Secondly, each surface dependency structure is translated

into a conceptual structure (or more than one if semantically ambiguous) using word

meaning descriptions. Finally, each conceptual structure is semantically evaluated.

The fundamental semantic computations on a text are to detect semantic anomalies,

ambiguities and paraphrase relations.

Semantic anomaly detection is very important to cut off meaningless computations.

Consider such a conceptual structure as (21), where ‘A29’ is the attribute ‘Taste’.

This locus formula can correspond to the English sentence ‘The desk is sweet’, which

is usually semantically anomalous because a ‘desk’ ordinarily has no taste.

(

∃

x)L(_,x,Sweet,Sweet,A29,Gt,_)

∧

desk(x) (21)

This kind of semantic anomaly can be detected in the following process.

Firstly, assume the commonsense knowledge of ‘desk’ as (22), where ‘A39’ re-

fers to the attribute ‘Vitality’. The special symbols ‘*’ and ‘/’ are defined as (23) and

(24) representing ‘always’ and ‘no value’, respectively. Another special symbol ‘_’

defined by (25) is often used instead of the variable bound by an existential quantifier.

(

x) desk(x)

↔

(

x) (…L*(_,x,/,/,A29,Gt,_)

∧

…

∧

L*(_,x,/,/,A39,Gt,_

)

∧

…) (22)

↔

(

∀

p,q)X

(p,q) (23)

L(…,/,…)

↔

∃

p) L(…,p,…) (24)

L(…,_,…)

↔

(

∃

x)L(…,x,…) (25)

Secondly, the postulates (26) and (27) are utilized. The formula (26) means that if

one of two loci exists every time interval, then they can coexist. The formula (27)

states that a matter has never different values of an attribute at a time

∧

⊃

. X

Y (26)

L(x,y,p1,q1,a,g,k)

L(z,y,p2,q2,a,g,k) .

⊃

. p1=p2

∧

q1=q2 (27)

Lastly, the semantic anomaly of ‘sweet desk’ is detected by using (21)-(27). That is,

the formula (28) below is finally deduced from (21)-(26) and violates the common-

sense given by (27), that is, “ Sweet ≠ / ”.

(

∃

x)L(_,x,Sweet,Sweet,A29,Gt,_)

L(_,x,/,/,A29,Gt,_) (28)

This process above is also employed for dissolving such a syntactic ambiguity as

found in S10. That is, the semantic anomaly of ‘sweet desk’ is detected and eventu-

ally ‘sweet coffee’ is adopted as a plausible interpretation.

(S10) Bring me the coffee on the desk, which is sweet.

If a text has multiple plausible interpretations, it is semantically ambiguous. In this

case, IMAGES will ask for further information in order for disambiguation.

For another case, if two different texts are interpreted into the same locus formula,

they are paraphrases of each other. The detection of paraphrase relations is very use-

ful for deleting redundant information.

IMAGES-M [3], the last version of IMAGES, can perform cross-media reference

between text and picture. For example, consider such somewhat complicated sen-

tences as S11 and S12. The underlined parts are considered to refer to some events

neglected in time and in space. These events are called ‘Temporal Empty Event

(TEE)’ and ‘Spatial Empty Event (SEE)’, symbolized as ‘

’

and ‘

’, respectively.

The concepts of S11 and S12 are given by (29) and (30) with the attribute ‘Trajec-

tory (A15)’.

(S11) The bus runs 10km straight east from A to B, and after a while

, at C it

meets the street with the sidewalk.

(

∃

x,y,z,p,q) (L(_,x,A,B,A12,Gt,_)

L(_,x,0,10km,A17,Gt,_)

L(_,x,Point,Line,A15,Gt,_)

L(_,x,East,East,A13,Gt,_))

•

(L(_,x,p,C,A12,Gt,_)

L(_,y,q,C,A12,Gs,_)

L(_,z,y,y,A12,Gs,_))

∧

bus(x)

∧

street(y)

∧

sidewalk(z)

∧

≠

q (29)

(S12) The road runs 10km straight east from A to B, and after a while

, at C it

meets the street with the sidewalk.

(

∃

x,y,z,p,q)(L(_,x,A,B,A12,Gs,_)

L(_,x,0,10km,A17,Gs,_)

L(_,x,Point,Line,A15,Gs,_)

L(_,x,East,East,A13,Gs,_))

•

(L(_,x,p,C,A12,Gs,_)

L(_,y,q,C,A12,Gs,_)

L(_,z,y,y,A12,Gs,_))

∧

road(x)

∧

street(y)

∧

sidewalk(z)

∧

≠

q (30)

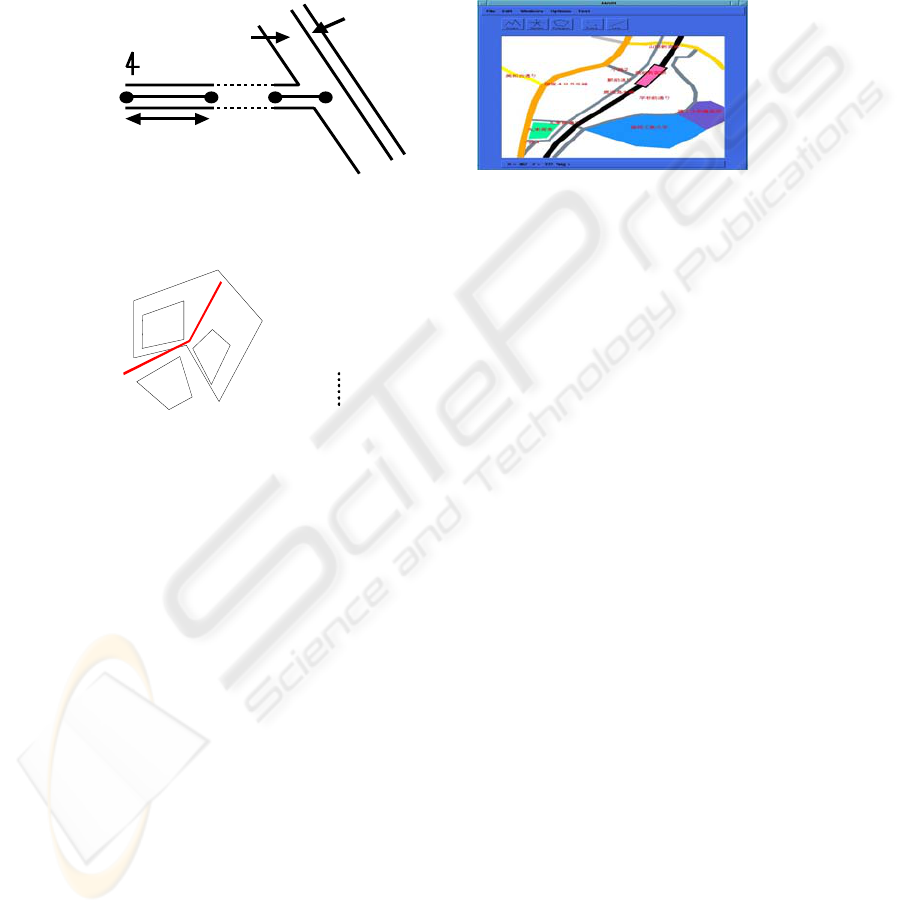
From the viewpoint of cross-media reference, the formula (30) can refer to such a

spatial event depicted as the still picture in Fig.4-a while (29) can be interpreted into a

motion picture. Figure 4-b shows one of real maps that IMAGES-M generated from

their corresponding locus formulas. IMAGES-M can also translate pictures into texts

via locus formulas as shown in Fig.5-a and answer questions about pictures as shown

in Fig.5-b.

road

street

sidewalk

10km

(a) (b)

Fig. 4. Pictorial interpretations of locus formulas: (a) an illustration of (30) and (b) a real out-

put of IMAGES-M.

The house A is in the town A.

The house B is in the town A.

The house A is 174 m

to the upper left of the house B.

The road B is between

the house A and the house C.

house A

house B

house

road

town A

road A

H: What is between the house A and the house B?

S: The road A.

H: Where do the road A and the road B meet?

S: In the town A.

H: Where do the road A and the road B separate?

S: In the town A.

(a) (b)

Fig. 5 Cross-media operations: (a) picture-to-text translation and (b) Q-A on the picture where

‘H’ and ‘S’ stand for ‘Human’ and ‘System’, respectively.

5 Discussions and Conclusions

The attribute spaces for humans correspond to the sensory receptive fields in their

brains. At present, about 50 attributes and 6 categories of standards concerning the

physical world have been extracted from a Japanese and an English thesaurus. Event

patterns such as shown in Fig.2 are the most important for our approach and have

been already reported concerning several kinds of attributes [1], [2]. The cross-

references between texts in several languages (Japanese, Chinese, Albanian and Eng-

lish) and pictorial patterns like maps were successfully implemented on our intelligent

system IMAGES-M. At our best knowledge, there is no other system that can per-

form cross-media reference in such a seamless way as ours [15], [16]. This leads to

the conclusion that our locus formula representation has made the logical expressions

of event concepts remarkably computable and has proved to be very adequate to sys-

tematize cross-media reference. This adequacy is due to its medium-freeness and its

good correspondence with the performances of human sensory systems in both spatial

and temporal extents while almost all other knowledge representation schemes are

ontology-dependent or spatial-event-unconscious.

Our future work will include establishment of learning facilities for automatic ac-

quisition of word concepts from sensory data [2] and human-robot communication by

natural language under real environments [4].

This work was partially funded by the Grants from Computer Science Laboratory,

Fukuoka Institute of Technology and Ministry of Education, Culture, Sports, Science

and Technology, Japanese Government, Project number 14580436.

References

1. Yokota,M. et al: Mental-image directed semantic theory and its application to natural

language understanding systems. Proc. of NLPRS’91 (1991) 280-287

2. Oda,S., Oda,M., Yokota,M. : Conceptual Analysis Description of Words for Color and

Lightness for Grounding them on Sensory Data. Trans. of JSAI,Vol.16-5-E (2001) 436-

444

3. Hironaka, D, Yokota, M.: Multimedia Description Language and Its Application to Cross-

media Referencing Systems. Proc. of DEXA workshop, Zaragoza, Spain (2004) 318-323

4. Yokota,M., Shiraishi,M., Capi,G.: Human-robot communication through a mind model

based on the Mental Image Directed Semantic Theory. Proc. of the 10th International Sym-

posium on Artificial Life and Robotics (AROB ’05), Oita, Japan (2005) 695-698

5. Dorr,B., Bonnie,J.: Large-Scale Dictionary Construction for Foreign Language Tutoring

and Interlingual Machine Translation. Machine Translation, Vol.12-4 (1997) 271-322

6. Zarri,G.P.: NKRL, a Knowledge Representation Tool for Encoding the Meaning of Com-

plex Narrative Texts, Natural Language Engineering. Special Issue on Knowledge Repre-

sentation for Natural Language Processing in Implemented Systems, Vol.3 (1997) 231-253

7. Sowa,J.F.: Knowledge Representation: Logical, Philosophical, and Computational Founda-

tions, Brooks Cole Publishing Co., Pacific Grove, CA (2000)

8. Miller,G.A., Johnson-Laird,P.N.:Language and Perception, Harvard University Press

(1976)

9. Langacker,R.: Concept, Image and Symbol, Mouton de Gruyter, Berlin/New York (1991)

10. Adorni,G., Di Manzo,M., Giunchiglia,F.: “Natural Language Driven Image Generation,”

Proc. of COLING 84 (1984) 495-500

11. Yamada, A. et al: “Reconstructing spatial image from natural language texts,” Proc. of

COLING 92, Nantes (1992) 1279-1283

12. Allen, J.F.: Towards a general theory of action and time. Artificial Intelligence, Vol.23-2

(1984) 123-154

13. McDermott,D.V.: A temporal logic for reasoning about processes and plans. Cognitive

Science, Vol.6 (1982) 101-155

14. Shoham,Y.: Time for actions: on the relationship between time, knowledge, and action.

Proc. of IJCAI\89, Detroit, MI (1989) 954-959

15. Eakins,J.P., Graham,M.E.: Content-based Image Retrieval: A report to the JISC Technol-

ogy Applications Programme. Institute for Image Data Research, University of Northum-

bria at Newcastle, January (1999)

16. Kherfi,M.L., Ziou,D., Bernardi,A.: Image Retrieval from the World Wide Web : Issues,

Techniques and Systems. ACM Computer Surveys, Vol.36-14 (2004) 35-67