Expanding Database Systems into self–verifying Entities

are J. Kristoffersen and Yvonne Dittrich

IT University of Copenhagen

⋆

DK-2300 S, Denmark

Abstract. The paper presents work-in-progress aiming at deploying runtime ver-

iﬁcation techniques to check whether the state changes in a database system

conform with temporal business rules given as expressions in temporal logic.

A framework for tailoring enterprise database systems with temporal business

rules is deﬁned and an algorithmic framework for checking temporal business

rules at runtime is presented. A prototypical implementation of a runtime veriﬁer

(called Veriﬁcation Server) based on this algorithmic framework is presented and

discussed.

1 Introduction

Runtime veriﬁcation is a branch of veriﬁcation in which a running program is super-

vised by a concurrrently running veriﬁer. In this paper we shall employ timed runtime

veriﬁcation, in which time will be an important parameter in the task of the veriﬁer.

Our idea is to use such a mechanism to monitor a running database system and hereby

at runtime check whether a sequence of states of a traditional database obey a set of

temporal business rules. In [5] an interesting framework for proving temporal proper-

ties of a database prior to execution is presented. That task is much harder and the

proof of correctness cannot be automated. In our approach, the proof (or dis–proof) is

established along with the execution of the database.

Temporal Business Rules and corresponding mechanism to check their success or

failure might be hard coded in business systems. Many such systems exists, like e.g. in

a library where customers (automatically) get a reclaim of their borrowed material after

one month. However, this approach restricts the ﬂexibility to re-deﬁne temporal rules

at all or at least to anticipated areas. Using runtime veriﬁcation techniques provides the

possibility to formulate and change general temporal business rules and to check them

without changing the business application.

Section 2 introduces the temporal logic we use as basis for temporal business rules

and the algorithmic base we developed for the checking these at runtime. Section 3

presents the design of an early prototype of the Veriﬁcation Server. Finally, in Section 4,

we sum up our ﬁndings so far and present our future line of research on the subject.

⋆

This work is supported by the project NEXT which is a joint effort between Microsoft Business

Solutions and the IT University of Copenhagen.

J. Kristoffersen K. and Dittrich Y. (2005).

Expanding Database Systems into self–verifying Entities.

In Proceedings of the 3rd International Workshop on Modelling, Simulation, Veriﬁcation and Validation of Enterprise Information Systems, pages 65-70

DOI: 10.5220/0002563000650070

 SciTePress

2 Temporal Business Rules

A state of a database is a pair (s, t) where s is a discrete component representing a

snapshot of all the data (or more precisely those data that are relevant for the temporal

business rules)and t is a time stamp. Using s, boolean constraints may be decided, such

as if the balance of a bank account is below a certain threshold. A temporal business rule

for a database is a speciﬁcation on how the internal state of the database may evolve over

time, and what should happen when a rule is satisﬁed (or the opposite) by the data in the

database: IF TC THEN Action

ELSE Action

, where TC is a temporal condition and

Actions 1 and 2 are some action to be performed. The core of our temporal conditions

are given by Timed LTL, LT L

, in the following abstract syntax (see also [1]):

φ ::= p | φ

∨ φ

| φ

∧ φ

| ¬φ | ALWAYS φ | ALWAYS

| EVENTUALLY φ | EVENTUALLY

φ,

where p ∈ AP and c ∈ IN.

The syntactic elements are: Atomic propositions, AP, which can be the occurence of

insert, update, delete or that an attribute in the database is above/below a certain thresh-

old. Further, logical connectives and then temporal operators ALWAYS and EVENTUALLY

both of which may be equipped with a time bound c. Intuitively they mean the fol-

lowing: Where ALWAYS φ denotes that the formula φ must hold in all timepoints,

ALWAYS

φ only requires φ to hold in the coming c time units. Conversely, the formula

EVENTUALLY

φ requires that formula φ is satisﬁed before c time units have passed,

and thus it is a more restrictive operator than EVENTUALLY which only requires the

sub–formula to hold at some point arbitrarily long away in the future. We shall use the

standard abbreviation such as expressing implication etc. as logical connectives, e.g.

⇒ φ

for ¬φ

∨ φ

and to use true instead of ¬p ∨ p. Using this language we may

formulate a temporal business rule for a vehicle assistance company in which the tem-

poral condition is the following, stating that assistances must not be given too frequent:

ALWAYS (new(C.Assistance) ⇒ ALWAYS

¬new(C.Assistance)).

Checking Temporal Business Rules The algorithm in the veriﬁcation server works by

a rewriting principle. For each new state encountered from the database, the algorithm

rewrites the temporal constraints to a new formula which states what should hold from

now on. Such a new formula is called a residual formula. In the algorithm below the

residual of formula φ with respect to a timed state σ

is denoted by φ/σ

Algorithm: Runtime Veriﬁcation procedure

Let σ = σ

. . . be a timed trace, let φ be a formula, let exists(σ

, time) be a

predicate which is true exactly when σ contains σ

and t

= time and let forceEvalua-

tion() be a method which returns the systems current state, at the current time.

ψ := φ/σ

; i := 1; time := 1; sit := SIT (ψ)

while ψ 6= true ∧ ψ 6= f alse do

if exists(σ

, time) ∧ s

6= s

i−1

then

ψ := ψ/σ

sit := SIT (ψ)

i + +

end if

if time = sit then

:= forceEvaluation()

ψ := ψ/σ

sit := SIT (ψ)

i + +

end if

time + +

end while

return ψ

Occasionally, the satisfaction (or falsiﬁcation) of a formula is not triggered by a

change of state in the database, but rather by the elapse of time alone. To ensure that the

algorithm is timely complete we let the veriﬁcation server compute the coming smallest

interesting timepoint (SIT) and insert an artiﬁcial state at such a time point

. See [4] for

a complete description of the algorithm. The rewrite principle is a timed extension of

the one in [3].

3 The prototypes

Based on the notation and algorithm introduced in the last section a second prototype

of the veriﬁcation server was implemented. The veriﬁcation server is designed as an

independent program running parallel to the business systems of the company. A ﬁrst

prototype parsed a rule in LTL notation and veriﬁed trace of state changes to a simple

(one-table) database complied with the rule. Recently the ﬁrst prototype was extended

to handle more than one rule with a more general way to interact with the database of

the business system. For each rule, an independent thread is started that takes care of the

veriﬁcation of that rule. This also allows the different rules to be based on different time

units. In the momentary version, the veriﬁcation server queries the database for relevant

state changes once each time unit speciﬁed as the basic time unit of the given rule. In

parallel a prototype for a rule builder is developed. We explore different alternatives

for the user interface to ﬁnd a notation for the temporal business rules and a way to

construct them that both leads to correctly formulated expressions in LTL and allows

for a meaningful interpretation from a business point of view.

The system so far looks as depicted in ﬁgure 1. When the business rule expert wants

to insert a new rule, he opens the rule builder (1)

. The system provides him with an

overview of the attributes he can base his rules on by querying the database for its data

model (2). He selects a table. When he is satisﬁed and presses the save button the rule

builder constructs an XML ﬁle (3) containing the LTL representation of the rule, the

time unit the rule is based on and sql statements to access the data deﬁning the states

the rule is observing. He then has to deﬁne what should happen in case of the violation

The discrete component of the artiﬁcial state is the one appearing in the most recent state

emitted by the database.

The numbers refer to the numbers in ﬁgure 1.

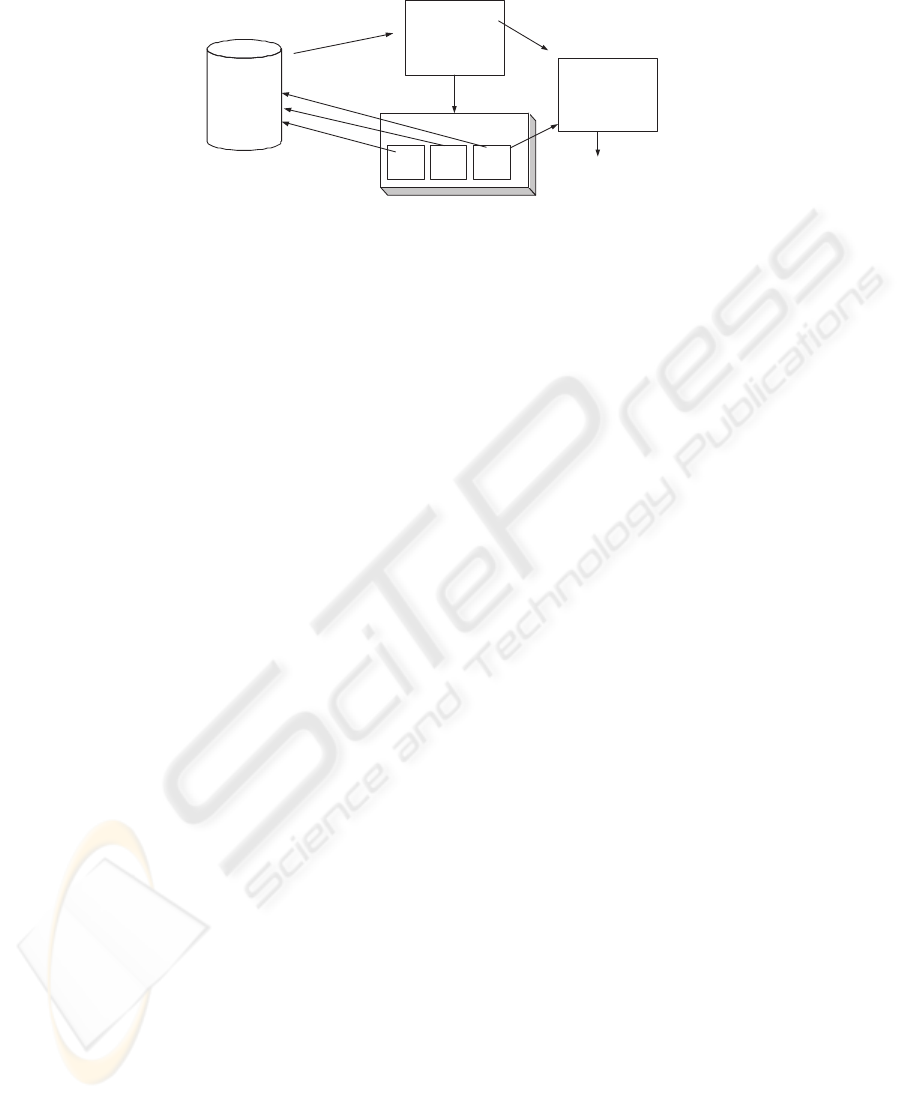
Business

Database

Rule Builder

M

e

t

a

d

a

t

a



a

b

o

u

t



d

a

t

a

m

o

d

e

l

.

SQL Queries

XML FIle

Tailor Notifier on what

to do in case of

success/violation

(2)

(1)

(3)

(7)

(8) Email

Notifier

Email

SMS

Business System

(4)

Verification Server

Thread 3Thread 2Thread 1

(5)

(6)

Fig.1. The system architecture.

of this rule in the administrator interface of the notiﬁer. (4) He decides that an e-mail

should be sent to the responsible person. The veriﬁcation server (5) parses the rule and

creates and internal representation of the rule for the transformation algorithm. A new

thread is started for the rule and parameterised with the respective sql queries and the

time unit for the rule (6). Each thread independently accesses the database to obtain the

information on state changes that are of interest when verifying the fulﬁllment of the

rule (7). When a rule is violated a notiﬁcation is sent to the notiﬁer. (4) The notiﬁer

sends an e-mail (8) to the one responsible for expensive customers as speciﬁed by the

business rule expert.

4 Conclusions and future research

The prototypes described in the previous section provide a proof of concept for this gen-

eral way of checking temporal business rules. Our prototype system can handle several

temporal rules based on the state of different items in the database. The thread based

design allows to deﬁne different time units for the different rules. It is possible to deﬁne

different reactions, in case a temporal rule is broken. Besides sending a notiﬁcation the

Veriﬁcation Server continues checking that the database changes comply with the dif-

ferent rules. However there are several issues that still are subject to future exploration.

We plan to set up the veriﬁcation server with a database to administer student projects

here at our university to explore the following issues.

Using the production Database as is, or deﬁning a speciﬁc view The solution the data-

base prototypes implement today offers the whole database to the business expert to

deﬁne temporal rules. Also the veriﬁcation server accesses the database without re-

quiring any speciﬁc functionality on the database side. This solutions is very general

and requires no changes at the database side. However, in a normalised database, the

data belonging together from the business point of view is often distributed over sev-

eral tables. Data might be stored in a speciﬁc way due to requirements in the business

systems. Production databases often contain a huge amount of tables of which only few

might be interesting when deﬁning temporal business rules. Deﬁning a speciﬁc view for

the veriﬁcation server would on the one hand allow to provide the user with a concise

overview of the kind of data relevant for the formulation of temporal business rules. It

would have the additional advantage that it would allow to change the database without

interfering with the already deﬁned temporal rules. On the other hand it would constrain

the formulation of rules to what is provided in the view. As long as changes in the tem-

poral business rules do not go beyond that scope, the changes can be implemented by

the business expert. In case other parts of the database have to be accessed, a database

expert has to extend the view.

Checking the whole data of only accessing changes In the momentary implementation

of the communication between the database and the veriﬁcation server, the veriﬁcation

server queries the production table for data that fulﬁlls the different boolean expressions

the rules are based on. This way relevant changes will automatically be recognized. For

large databases this might lead to performance problems, especially when short time

intervals are used as a base for the rules.

Another solution would be to only access changes to the data under observation.

This would require to create a buffer and speciﬁc triggers as part of the database based

on the deﬁnition of the rules in the rule builder. This should be possible but would

require to change the business database itself. The rule builder module would have

to keep track of the changes it implemented in the database and would have to undo

them in a controlled way when a temporal rule is change or erased. A third possibility

would be to implement an asynchronous observer pattern between the database and the

veriﬁcation server. Here again, the database would have to be adapted based on the rules

deﬁned by the user to create the events the veriﬁcation server needs for checking the

temporal business rules.

Finding a suitable user interface Research on End-User Development has shown that

users are able to handle complex computations deﬁned in a formal way when the for-

malisms are presented in a professionally meaningful way. [6][8] We plan to experiment

with different kinds of user interfaces in order to ﬁnd a suitable way to represent the

data temporal rules can be formulated about and to support the user in deploying the

possibilities that formalism offers. From a technical point of view the notiﬁer and the

rule builder are two very different parts of the system. From a business perspective the

deﬁnition of temporal rules and the deﬁnition of what should happen in case of a vi-

olation belong together. Here the two tailoring interfaces must be integrated. Another

issue that needs more exploration is the requirements such a system poses on the or-

ganization: when business rules can be (re-)deﬁned, the organization has to implement

procedures to decide what rules to implement.[7][2]

Performance So far, we only tested the veriﬁcation server based on toy examples. Im-

plementing a sharp version together with the project database of our university will

give us the opportunity to evaluate the design and performance of the veriﬁcation server

when interacting with a small but realistic database. The performance of the concrete

veriﬁcation algorithm as well as the inﬂuence of the different design possibilities for

the interaction with the database can then be evaluated under more realistic conditions.

Acknowledgments

Thanks to Bente B. Petersen, Divya R. Malemane, Bue Pedersen, Ulrik D. Olsen who

together developed the different prototypes the article is based on as part of their Master

Theses.

References

1. Alur, R., Henzinger, T.: Logics and Models of Real Time: A Survey. Real Time: Theory in

Practice, Lecture Notes in Computer Science 600, Springer-Verlag, (1992), pp. 74-106.

2. Dittrich, Y., Lindeberg, O.: Designing for Changing Work and Business Practices. In: N.

Patel (ed.). Evolutionary and Adaptive Information Systems. IDEA group publishing, (2002).

3. Havelund, K., Ruso, G.: Monitoring Programs using Rewriting. Automated Software Engi-

neering (ASE’01), San Diego, California, (2001), IEEE Computer Society.

4. Kristoffersen K., Pedersen, C., and Andersen, H. R.: Runtime Veriﬁcation of Timed LTL

using Disjunctive Normalized Equation Systems. Appears in Issue 89.2 of Electronic Notes

in Theoretical Computer Science (2003).

5. Kung, C. H.: A Temporal Framework for Database Speciﬁcation and Veriﬁcation. Proceed-

ings of the Tenth International Conference on Very Large Data Bases, Singapore, August,

(1984).

6. Patern, F., Klann, M., Wulf, V.: Research Agenda and Roadmap for EUD. Deliv-

erables of the Network of Excellence on End-User Development, December, (2003).

(http://giove.cnuce.cnr.it/eud-net.htm)

7. Trigg, R., Bødker, S. From Implementation to Design: Tailoring and the Emergence of Sys-

tematization in CSCW. Proceedings of the CSCW 94, ACM-Press, New York, (1994), pp.

45-55.

8. Stiemerling, O., Kahler, H., Wulf, V.: How to make software softer- Designing tailorable

applications. Proceedings of the Designing Interactive Systems (DIS) (1997).