A Multi-Resolution Learning Approach to Tracking

Concept Drift and Recurrent Concepts

Mihai M. Lazarescu

Faculty of Computer Science, Curtin University,

GPO Box U1987, Perth 6001, W.A.

Abstract. This paper presents a multiple-window algorithm that combines a

novel evidence based forgetting method with data prediction to handle different

types of concept drift and recurrent concepts. We describe the reasoning behind

the algorithm and we compare the performance with the FLORA algorithm on

three different problems: the STAGGER concepts problem, a recurrent concept

problem and a video surveillance problem.

1 Introduction

Incremental learning is used more and more often today across many domains. The

reason for the increased focus on incremental learning techniques is that the learning

is dynamic and hence it is more applicable to real world situations such as on-line

processing or mining large datasets. An important issue of incremental learning which

this work addresses is that of tracking and adapting to changes in the data, speciﬁcally

we refer to the problem of concept drift. A brief deﬁnition of the problem of concept

drift is as follows: “In many real-world domains, the context in which some concepts

of interest depend may change, resulting in more or less abrupt and radical changes

in the deﬁnition of the target concept. The change in the target concept is known as

concept drift” [8]. The main difﬁculty in tracking concept drift is that there is no prior

knowledge of the type, pace and timing of the change that is likely to occur. Hence

model based or time series based approaches are not suited for this problem.

A crucial aspect of the concept drift problem is forgetting. The algorithms developed

to handle concept drift generally use a time based mechanism to control the forgetting

process which generally leads to two problems: useful information is being discarded

and the system converges more slowly to the target concept. Furthermore, the systems

simply react to changes rather than attempt to predict and classify the changes in the

data.

This paper presents a multiple window approach to track different types of concept

drift. The algorithm attempts to interpret current data as well as detect, predict and

quickly adapt to future changes in the concept. The system is designed to work in an

on-line scenario where the data consists of a sequential stream of examples which are

used by the system to derive a concept description that is consistent with the information

observed.

The work presented makes three novel contributions. The ﬁrst novel aspect of the

research is that the algorithm uses a usefulness based approach to control the forgetting

M. Lazarescu M. (2005).

A Multi-Resolution Learning Approach to Tracking Concept Drift and Recurrent Concepts.

In Proceedings of the 5th International Workshop on Pattern Recognition in Information Systems, pages 52-62

DOI: 10.5220/0002568900520062

 SciTePress

mechanism used to discard data from the system’s memory. Rather than using a time

based approach, the forgetting mechanism analyses the newly observed data instance

to determine how well it ﬁts with the rest of the instances in the system’s memory and

the current concept deﬁnition. Based on the the rest of the data, the mechanism also

determines if the new instance is a likely indicator of a change in the concept. Once the

usefulness of the instance has been estimated, the system checks both the usefulness and

age of the instance to determine whether or not the the instance is to be discarded. The

second contribution is that the algorithm predicts the rate of change to give the system a

pro-active approach to the data and thus improve the accuracy of the concept tracking.

The algorithm consistently checks the current rate of change and estimates (based on

past history) what the future rate of change is likely to be. This information is used to

improve the control over the size of the larger dynamic data window which acts as the

memory of the system and it allows for a faster adaptation to changes in the concept.

The third contribution is the representation used for the concepts tracked. Rather than

storing a simple generalization of the data observed, we represent the concept through a

combination of instance generalizations, data predictors and the rate of change observed

when concept was stable. Moreover, we use a knowledge repository to store old concept

descriptions to avoid having to “re-learn” recurrent concepts.

2 Related Work

The issue of concept drift has been investigated for many years and several systems

have been developed to address the problem of concept drift. The aim of the research

in this area is to develop algorithms that will allow a system to adapt concepts quickly

to permanent change while avoiding any unncessary changes if the change observed is

determined to be virtual (temporal) or noise.

The ﬁrst system developed to deal with concept drift was STAGGER [7]. The learn-

ing method employed by STAGGER is based on a concept representation which uses

symbolic characterizations that have a sufﬁciency and a necessity weight associated

with them. As the system processes the data instances, it either adjusts the weights

associated with the characterizations or it creates new ones.

The FLORA family of algorithms implements a moving window approach to deal

with concept drift [9, 2]. FLORA2 is a supervised incremental learning system that

uses a stream of positive and negative examples to track concepts that change over

time. FLORA2 has a heuristic routine to dynamically adjust its window size and uses a

better generalization technique to integrate the knowledge extracted from the examples

observed. FLORA2 has been improved ﬁrst by adding new routines to better handle

noise (FLORA3) and to handle the issue of recurring contexts (FLORA4).

A different approach to dealing with concept drift was used in the AQ-PM [5] and

SPLICE [1] batch learning systems. AQ-PM is a partial memory system, [5, 6,4]. The

system analyzes the training instances and selects only “extreme examples” which it

deems to lie at the extremities of concept descriptions. SPLICE [1] is an off-line meta-

learning system that uses contextual clustering to deal with concept drift that occurs as

a result of hidden changes in contexts. The learning process assumes that some con-

sistency exists in the data and the system groups together sequences of instances into

intervals if the instances appear to belong to the same concept.

3 Motivation for new approach

Algorithms developed to deal with drift implement some type of moving window that

acts as the system’s memory. The instances in the memory are used to track and update

a target concept. As the window moves over data observed, new instances are added to

the memory while the oldest instances are discarded. Instances once forgotten cannot be

recalled. The aim is for the algorithms to adapt quickly to the changes observed in the

data while still being robust to noise or virtual drift [9]. If a true change is detected in the

data, the system should remove all old and irrelevant information from the memory and

update the concept description to keep it consistent with the data observed. If the change

detected is just noise or virtual drift then the system should not make any changes to

the concept description and should remove all the misleading data instances from the

memory. Hence tracking concept drift accurately depends on the capacity of the system

to make the correct decision when discarding information from the system’s memory.

If the system either discards instances which are still relevant or keeps instances that

are no longer useful then its tracking will be severely affected.

To deal with this problem most algorithms use a time-based forgetting mechanism

where an instance ages over time as more new instances are observed. There are three

problems with this approach. The ﬁrst is the assumption that the oldest instances in

the window are less relevant and hence should be the ﬁrst to be removed from the

window. The second problem is that all data instances stored in the window have equal

importance in the processing involved on the target concept. These two assumptions are

not correct especially in applications where the data contains random noise or involves

some virtual change in the concept. For example, consider the case where the data

instances observed have been consistent for a period of time but the last few instances

have been affected by random noise. Using a simple time based forgetting approach,

older but noise free instances would be discarded from the memory while the newer

but noise affected instances would be kept which would be incorrect. Furthermore, as

all instances would be considered to be of equal importance, then the most recent noise

affected instances would affect the target concept deﬁnition as changes would be made

to keep the deﬁnition consistent with the data observed.

Another major problem with most existing algorithms that track drift is that they

lack a mechanism for predicting and estimating future data changes. Prediction is very

important for two reasons. First, it can be used to control the size of the system’s mem-

ory. Different types of change have different requirements in terms of forgetting. If

the change involved is abrupt, then the size of the memory needs to be reduced by a

large margin to allow the system to adapt faster to the changes. However, if no change

is detected, then the size of the memory can be increased to allow for a more accu-

rate description of the target concept. If the system has a good estimate of the rate of

change, then it can reduce/increase the memory size accordingly. Second, prediction

can be used as a cross-validation tool on past decisions to discard data and modify the

memory size. This is particularly important for the approach described in this paper as

the instances are not removed from all windows at the same time (the larger window

keeps data instances for a longer time interval). If the change is predicted correctly,

then subsequent data instances will provide conﬁrmation in the form of more accurate

tracking and possibly fewer changes made to the memory size. The following section

covers a number of basic deﬁnitions that are used through the remainder of the paper

and describes in detail the forgetting and prediction mechanisms developed to address

the problems outlined above. The section also includes the description of the overall

tracking algorithm. Finally, current algorithms store only generalizations of the data

observed in the window and generally lack the capacity to handle recurrent concepts.

This is a signﬁcant drawback as the system has to “re-learn” recurrent concept deﬁni-

tions (but were forgotten when the concepts changed) and thus its tracking accuracy is

badly affected.

4 Multiple Window Approach with Relevance Based Forgetting

and Prediction Analysis

4.1 Preliminaries

The different types of concept drift can be deﬁned in terms of two factors: consistency

and persistence. Consistency refers to the change that occurs between consecutive in-

stances of the target concept.

Let θ

be the concept at time t where t is 0, 1, 2, 3, ..., n and let ǫ

=θ

-θ

t−1

be the

change in the target concept from time t-1 to t. A concept is considered to be consistent

if and only if ǫ

≤ǫ

, where ǫ

is termed the consistency threshold. Let the size of the

window which represents the system’s memory be X. A concept is considered to be

persistent if and only if ǫ

t−p

, ǫ

t−p+1

, . . ., ǫ

≤ ǫ

and p ≥

, where p represents the

persistence of the change (the interval length of consecutive observations over which the

change is consistent). If the change observed in the target concept is both consistent and

persistent then the drift is considered to be permanent. If the change is consistent but

not persistent then the drift is considered to be virtual. Finally, if the change observed

is neither consistent or persistent then the drift is considered to be noise.

4.2 The Evidence Based Forgetting Module

To address the problems associated with the time based forgetting approach outlined in

section 3, a new evidence based forgetting method has been developed. The idea behind

the approach is that an instance needs to be stored in the window if and only if there

is evidence that justiﬁes its presence. The evidence can come in two forms. First, an

instance is relevant to the target concept and the rest of the data observed. Second, an

instance is a likely indicator of a change in the concept. Hence if an instance has no

evidence justifying its inclusion in the system’s memory, regardless of its “age”, then

it should be discarded. Each instance stored in the moving window is assigned three

values: an evidence value, an age value and a change indicator value. All three values

are updated each time a new instance is added to the window. The age value (age) is

derived by checking its position in the system’s memory. The older the instance the

higher the age of the instance. The evidence value (ev) of the instance is determined

by how well the instance matches the current target concept description and the other

instances stored in the system’s memory. The better the match the higher the evidence

value. The change indicator value (∆) depends on the evidence value. In some cases

a newly observed instance may not match either the target concept or the rest of the

instances in the system’s memory. In this case the instance is ﬂagged as a potential

indicator that a change is about to occur in the target concept and hence its removal

from the window will be delayed. The delay is user deﬁned.

This type of forgetting offers several advantages. First, the instances are discarded

from the memory based on how useful they are to the target concept and the data

observed rather than based only on their age. Second, it helps the system to identify

quickly the forgetting point φ in the data (the instance which indicates the start of per-

manent drift in the target concept). As all instances have a change indicator value, the

system only needs to ﬁnd the instance that has the highest value to ﬁnd the forgetting

point. Furthermore, the evidence values can be used to help determine the type of drift

in the concept. This is because the drift is reﬂected in the way in which the evidence

value varies over time. Consider the following example. Let θ

be the concept tracked at

time t and data instances stored in the memory at time t be denoted by I

, I

,...,I

Also let the new instance to be added to the memory be denoted by I

n+1

If the instance I

n+1

is the start of permanent drift in the concept, then the evidence

value ev assigned to the instance will be low as the instance does not match well θ

Similarly the age value age will also be low as the instance has just been added to the

window. However, the change indicator value ∆ will be high making I

n+1

a potential

candidate for the forgetting point in the data. Because of the persistent change in the

concept, as more data is observed, the newly observed instances will match I

n+1

, thus

incrementing both its ev and ∆ values while the older instances seen before I

n+1

have

their ev values decremented. Also as more new instances that match I

n+1

are added

to the window and old ones are discarded, the concept deﬁnition changes and becomes

a better match for I

n+1

thus further incrementing its ev value. If the instance I

n+1

the start of virtual drift in the concept or is just noise, then both the ev and age values

assigned to the instance will be low (the instance is new but does not match well θ

)

while the ∆ value will be high making I

n+1

a potential candidate for the forgetting point

in the data. However, as more data is processed, the ev and ∆ values have a different

behaviour when compared to the reinforcement seen when dealing with permanent drift.

Virtual drift does have consistency but lacks persistence. Hence the ev and ∆ values for

instance I

n+1

are incremented only for a short interval of time. As soon as the data

reverts back , the instance I

n+1

will not longer match the most recently observed data.

Therefore its ev and ∆ values will be decremented and the instance will quickly be

discarded from the window. If instance I

n+1

is only noise then it is unlikely to match

any of the subsequent instances since noise has neither consistency nor persistence.

Hence, both its ev and ∆ values will be decremented as more data is processed and the

instance will be forgotten as soon as the user predeﬁned delay expires.

4.3 The Prediction Analysis Module

To improve the tracking performance of the algorithm, a prediction component was

added. The original competing windows algorithm (CWA) [3] on which this work is

based, used an estimate of the change in the concept to handle drift in the target concept

. This approach has been modiﬁed to allow the system to predict the future rate of

change ǫ

The rate of change ǫ

prediction involves the analysis of the short term history of the

change observed in the target concept. If the history indicates that the rate of change has

been consistent then the predicted rate of change is the average of the past ǫ

. However,

if the rate of change has not been consistent, then the prediction is derived based on the

short term trend of past ǫ

and the difference between the predicted ǫ

and the actual ǫ

Hence, if the trend shows an increasing rate of change and the true rate is still larger

than the predicted rate, then future predicted values are increased. The analysis of ǫ

used to control the size of the system’s memory. If the actual ǫ

is signiﬁcantly larger

than the predicted ǫ

, then the size of the current window is too large, and it needs to be

reduced. This in turn is used to remove more instances with low evidence value in the

window. However, if the predicted ǫ

is larger, then the window size can be increased

and it may not be necessary to forget any of the instances currently in the memory.

4.4 Algorithm Description (MRL)

Overall the algorithm attempts to detect and track changes in the target concept using a

multi-resolution approach. The algorithm uses two windows which compete to produce

the best interpretation of the data. The reason for using multiple windows is that in

order to deal with all types of drift, more than one interpretation of the data is needed.

Furthermore, the use of two windows allows a more gradual forgetting as data discarded

from the smaller of the two windows is not discarded from the larger window. The

concept tracked, as mentioned in the introduction, is represented by a combination of

instance generalizations, data predictors and the rate of change observed when concept

was stable. Both the instance generalization and the data predictors are in essence partial

instances that describe the common characteristics of the data observed in the window.

The main body of the algorithm is shown in Figure 4.4 while the forgetting and

prediction components are shown in Figures 4.4 and 4.4 respectively. The notations

used are as follows: θ

is the concept tracked at time t, l

(w ) is the length of the window

w, ǫ

(w ) is the rate of change in window w, Ψ is the forget set.

The processing done by the algorithm is outlined below. Initially, after the average

of the data vectors in the window has been computed, the number of observations over

which the change is consistent is set to 1. Then for each subsequent data sample ob-

served, the system attempts to determine the rate of change. To do this, the concept def-

inition for each of the two windows is updated at each step t using the formula ¯x

(w ) =

1/|w |

|w|−1

i=0

t−i

. This newly derived concept deﬁnition is then used to compute the

change in the window. The change is obtained by subtracting the concept value in the

window at time t-1 from the concept value in the window at time t. The current change

is then compared with the consistency threshold. If the current change in the window is

smaller than or equal to the consistency threshold ǫ

, then the persistence value for the

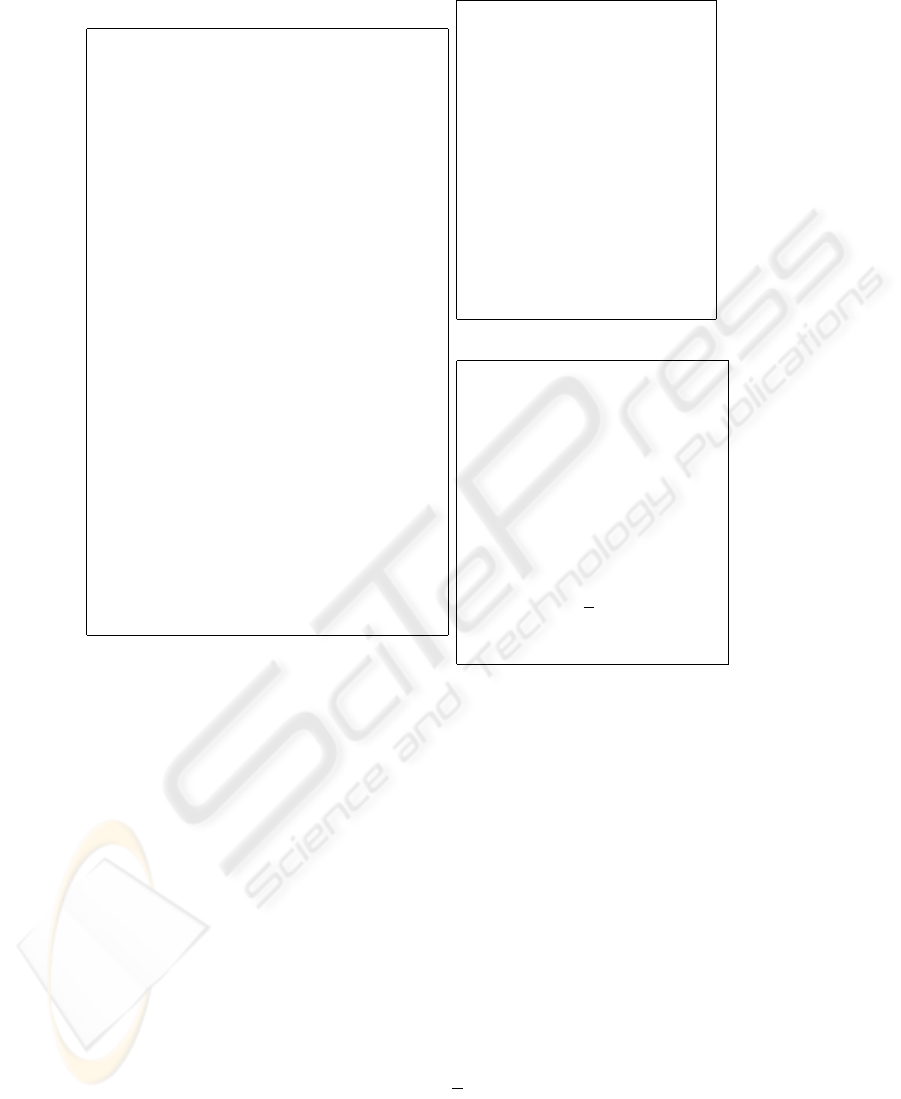
Begin

For each time t:

For each window w ∈ {S, M}:

Increase |w|++ if not already at maximum size

Compute the change ǫ

(w)

/* Update the persistence value for the window */

If |ǫ

(w)| > ǫ

then

Reset the persistence for the window p(w) = 1

Update consistent change ǫ

(w) = ǫ

(w)

Else

/* Increment persistence value for the window */

p(w)++

Call Do-Forgetting;

Call Do-Prediction;

/* Resetting smaller window */

If reset-ﬂag = true

Remove all instances before φ in w

Store concept θ

∗

) in repository

Empty Ψ for small window

/* Resetting larger window */

If p(w) = 2|w| then

Set the next larger window size to 2|w|

Else If reset-ﬂag = true

Remove all instances before φ in w

Store concept θ

∗

) in repository

Empty Ψ for medium window

/* Compute estimated concept */

If w is reset then

Recompute ¯x

(w) and ǫ

(w)

Set concept θ

(w) = ¯x

(w)

Else

Set concept θ

(w) = θ

t−1

(w) + ǫ

(w)

/* Return the concept from best window */

Best window w

∗

= arg max

(w)

Return θ

∗

)

End

Fig.1. The main algorithm.

Do-Forgetting;

For each window w ∈ {S, M}:

/* Determine the instance relevance */

For each instance I in current w

Increment ag e

For each instance J in current w

If Match(I,J)

Increment ev and ∆ of I

Else

Decrement ev and ∆ of I

/* Reset the forgetting point */

If ∆ of I is largest observed

φ = I

/* If instance has low relevance or

instance has high age

then add it to the forget set */

If ev and ∆ < 0 OR age < max-age

Add I to Ψ

Fig.2. The Forgetting Module

Do-Prediction;

For each window w ∈ {S, M}:

/* Do rate of change prediction */

Check p(w)++

If ǫ

consistent

predicted ǫ

= ¯ǫ

/* If the rate of change is inconsistent

compute a new estimate and

check repository for recurrent

concepts*/

Else

Rate-Difference = |predicted ǫ

- ǫ

Check ǫ

Trend

Check-Repository

For i = 0 to

Compute predicted ǫ

reset-ﬂag = true;

Fig.3. The Prediction Module

window p, is incremented by one. Else the persistence value for the window is reset to

The algorithm then proceeds to analyse the data samples stored in the window to

determine their usefulness as well as to identify possible forgetting points (φ). Each

instance in the window is matched ﬁrst against the current concept deﬁnition and then

against the other instances in the window. For each match found, the evidence value

ev of the instance is incremented. Furthermore, if the instance is likely to be a change

indicator, for each match the ∆ value is also incremented. However, if a mismatch is

found then the ev and ∆ values are decremented. The instance that has the largest ∆

value is considered to be the new forget point φ. When all instances in the window have

been processed, the algorithm selects those with very low ev and ∆ values as well as

high age values and adds them to the forget set (Ψ).

The algorithm also checks the predicted rate of change. If the rate of change is

consistent then the predicted rate for the next

time steps is set to the mean of the rate

of change observed in the past. However, if the rate of change is not consistent, then

the difference between the predicted and actual rate of change is computed. Next, the

algorithm checks the repository for old concept descriptions that may match the newly

seen data. If a match is found, then the concept is reset to the old deﬁnition. The trend

of the change observed is analysed and used to compute a new set of predicted values

for the next

time steps. The reset ﬂag is also set to indicate the size of the window

should be reduced if the true rate of change is greater than the predicted rate.

Next, the algorithm deletes the instances in Ψ and makes changes to the window size

if required. If the reset ﬂag is set to true then all instances observed before the forget

point are discarded from the window and the size of the window is reduced. However,

the size of the larger window can also be reset as a result of the consistency observed

in the smaller window. If the change in the small window is persistent for more than

2S observations, then enough consistency has been found in the small window and the

medium window is reset. When the medium window is reset, its size is reduced from

M to 2S. At any time instance, a concept has a description in each of the 2 windows,

and a degree of persistence for the concept in that window. The best concept deﬁnition

is given by the description of the largest sized window that has longest consistency.

The algorithms requires that two parameters be set by the user. The ﬁrst parameter

deﬁnes the length of the history to be used when analysing the trend of the change

in the concept. The algorithm uses as default a value of

for the processing which

experiments done have indicated to be sufﬁcient to generate good estimates. The second

parameter deﬁnes the delay used to prevent the removal of instances that have low

usefulness but are likely indicators of change in the concept. The default value for the

delay was set at

but in noisy domains a shorter delay may be more effective.

5 Results

The algorithm was applied to two problems that involve concept drift. The ﬁrst was

the STAGGER concepts problem which is the standard benchmark used to test concept

drift tracking algorithms. The second problem involved the interpretation of an average

frame extracted from video surveillance.

5.1 STAGGER Scenario

The STAGGER concepts scenario is described in detail in [7] and involves a dataset

of 120 instances divided into 3 stages. The target concept changes at an interval of

40 instances. The aim is to track the concept with the highest possible accuracy while

adapting to the changes observed in the data. The experiment was run 100 times and

the average accuracy of the system is shown in Figures 4 (noise free data) and 5 (data

contained 20% noise). The results from using FLORA on the same data are also shown

for comparison purposes. The reason for selecting FLORA is because it uses the most

popular form of tracking drift with a single dynamic window and it implements heuris-

tics routines to adjust the window size based on the changes detected in the data. The

results show that the algorithm presented in this paper tracks the concept with high

accuracy and adapts very quickly to the changes in the data. The performance of the al-

gorithm decreases as more noise is added to the data both in terms of tracking accuracy

and speed with which it converges to the target concept. However, when compared with

FLORA, the new algorithm’s performance is better in all three cases and in particular it

adapts faster to the changes in the data.

5.2 Recurrent Concept Scenario

The second experiment used to test the algorithm involved tracking a recurrent concept.

The scenario involved a modiﬁed version of the STAGGER concept problem. In this

case we added a fourth stage of 40 instances. The concept from the ﬁrst 40 instances

was repeated in the third stage of the experiment. The concept from the second stage

was repeated in the fourth stage of the experiment. The success was measured by how

well the system handled the repeated concept. The experiment was run 100 times and

the average accuracy of the system is shown in Figures 6 (noise free data) and 7 (data

contained 20% noise). The results show that the system adapted signiﬁcantly faster to

the target concept when the concept was repeated. FLORA is also able to recognise past

concepts but its accuracy is slightly lower due to its reliance on instance based concept

generalizations.

5.3 Background Frame Problem

The third experiment involved tracking changes in the average frame computed from

video surveillance. A simple way to detect motion in surveillance is to analyse the

differences between a preset video frame and the frames obtained from the live sur-

veillance. The problem is that in many cases, gradual changes in the background due

to changes in the environment conditions (such as faulty ﬂashing neon-lights) are in-

terpreted as actual motion which results in a large number of false alarms. The dataset

used for this problem contained 300 video frames from a stationary camera as shown in

Figure 8. The lighting conditions change four times over the 300 frames. The aim for

this problem was to track the changes in the average frame as accurately as possible.

The results are shown in Figure 9. The plot shows the true concept value over the 300

instances as well the concept value derived by the drift tracking algorithm. Overall, the

accuracy of the algorithm is very good and there is little delay before the concept is

adapted to the changes in the data.

6 Conclusions

This paper describes a multiple window algorithm that combines evidence based for-

getting and prediction analysis to track concept drift. The work presented makes two

novel contributions: it introduces a new mechanism for forgetting and it uses a pre-

diction method to control the size of the windows and thus allow a more pro-active

interpretation of the data. The algorithm was tested using two datasets: the STAGGER

concepts problem and a background frame tracking problem. The results obtained show

that the algorithm adapts very quickly to changes in the data and tracks drift with very

good accuracy.

100

120

0 20 40 60 80 100 120

Classification Accuracy

Training Instances Processed

"MRL"

"FLORA"

Fig.4. Classiﬁcation results of data without

noise.

100

120

0 20 40 60 80 100 120

Classification Accuracy

Training Instances Processed

"MRL"

"FLORA"

Fig.5. Classiﬁcation results of data with 20%

noise.

"MRL"

100

120

0 20 40 60 80 100 120

Classification Accuracy

140

160

Training Instances Processed

"FLORA"

Fig.6. Classiﬁcation results of data without

noise.

"MRL"

100

120

0 20 40 60 80 100 120

Classification Accuracy

140

160

Training Instances Processed

"FLORA"

Fig.7. Classiﬁcation results of data with 20%

noise.

Fig.8. Surveillance Image.

0.5

1.5

0 50 100 150 200 250 300

Luminance Intensity Concept Value

Video Frame Number

"True_Concept_Value"

"MRL_Concept_Value"

Fig.9. Classiﬁcation results for background

frame problem.

References

1. M. Harries and K. Horn. Learning stable concepts in a changing world. Lecture Notes in

Computer Science, 1359:106–122, 1998.

2. M. Kubat and G. Widmer. Adapting to drift in continuous domains. Lecture Notes in Computer

Science, 912:307–312, 1995.

3. Mihai Lazarescu, Svetha Venkatesh, and Hai Hung Bui. Using multiple windows to track

concept drift. Intelligent Data Analysis, 8(1), 2004.

4. M. Maloof and R. Michalski. Selecting examples for partial memory learning. Machine

Learning, 41:27–52, 2000.

5. M.A. Maloof. Progressive partial memory learning. PhD thesis, School of Information Tech-

nology and Engineering, George Mason University, Fairfax, VA, 1996.

6. M.A. Maloof and R.S. Michalski. AQ-PM: A system for partial memory learning. In Pro-

ceedings of the Eighth Workshop on Intelligent Information Systems, pages 70–79, Warsaw,

Poland, 1999. Polish Academy of Sciences.

7. J. Schlimmer and R. Granger. Beyond incremental processing: Tracking concept drift. In

Proceedings of AAAI’86, pages 502–507. AAAI Press, 1986.

8. Gerhard Widmer. Combining robustness and ﬂexibility in learning drifting concepts. In Eu-

ropean Conference on Artiﬁcial Intelligence, pages 468–472, 1994.

9. Gerhard Widmer and Miroslav Kubat. Effective learning in dynamic environments by ex-

plicit context tracking. In Machine Learning: ECML-93, European Conference on Machine

Learning, Proceedings, volume 667, pages 227–243. Springer-Verlag, 1993.